 hujung hadapan web
hujung hadapan web Tutorial H5
Tutorial H5 Cara mudah untuk melukis lengkung menggunakan petua tutorial Canvas_html5 HTML5
Cara mudah untuk melukis lengkung menggunakan petua tutorial Canvas_html5 HTML5Cara mudah untuk melukis lengkung menggunakan petua tutorial Canvas_html5 HTML5
Kaedah lengkung yang disertakan dengan Canvas2D
Baru-baru ini saya telah mengkaji pengiraan badan lembut 3D, jadi saya cuba mengejar beberapa pengetahuan. Ia selalunya melibatkan beberapa analisis berangka, terutamanya pelbagai algoritma interpolasi lengkung. Tiba-tiba saya teringat bahawa Canvas2D sendiri juga boleh melukis lengkung, menggunakan lengkung Bezier kuadratik dan kubik. Sebenarnya, saya tidak pernah menggunakan kaedah ini, jadi mari cuba sekarang ~
Artikel ini hanya bercakap tentang lukisan lengkung mudah, dan saya tidak akan bercakap tentang banyak prinsip yang rumit. Selain itu, prinsip Bezier Curve adalah sangat mudah Anda boleh memahaminya dengan melihat Wikipedia. Sebenarnya, banyak lukisan lengkung mudah dalam alatan lukisan menggunakan lengkung Bezier Jika anda telah menggunakan lengkung dalam alatan lukisan yang disertakan dengan Windows, anda mesti biasa dengannya. Mula-mula anda boleh menyeret keluar garis lurus, dan kemudian klik kedudukan tertentu untuk memesongkan garis lurus. Tindakan menyeret awal adalah untuk menentukan dua bucu lengkung, dan tindakan mengklik adalah untuk menambah titik perantaraan. Alat lukisan yang disertakan dengan Windows menggunakan lengkung Bezier padu, dan anda boleh menambah dua titik perantaraan. Keluk Bezier adalah berbeza daripada interpolasi polinomial umum Titik tengahnya hanya digunakan sebagai titik kawalan, bukan bucu yang mesti dilalui oleh lengkung. Dan ia juga boleh membuat lengkung tertutup. Canvas2D menyediakan dua kaedah untuk melukis lengkung
quadraticCurveTo: Quadratic Bezier Curve
bezierCurveTo: Cubic Bezier Curve
Garisan dilukis bermula dari kedudukan semasa Anda boleh menggunakan kaedah moveTo untuk menentukan kedudukan semasa. Selepas anda mempunyai kedudukan permulaan lengkung, anda juga memerlukan titik tengah dan kedudukan penamat. Hanya hantar koordinat kedudukan ini kepada fungsi lukisan. Contohnya, lengkung Bezier kuadratik memerlukan titik perantaraan dan kedudukan akhir, jadi dua koordinat perlu dihantar ke fungsi kuadratikCurveTo. Koordinat terdiri daripada x dan y, yang bermaksud fungsi ini mempunyai 4 parameter. bezierCurveTo adalah sama, kecuali ia mempunyai dua titik perantaraan. Mari gunakannya di bawah
- "2d"); //Garis lurus biasa
- g.beginPath();
- g.strokeStyle=
- "#CCC"; g.moveTo(0,0); g.lineTo(200,0);
- g.lineTo(0,200); g.lineTo(200,200);
- g.stroke();
- //Keluk Bez
- g.beginPath();
- g.strokeStyle= "#F00"
- ; g.moveTo(0,0);
- g.bezierCurveTo(200,0, 0,200, 200,200); g.stroke();
- Ini memberikan empat mata mengikut trajektori berbentuk Z dan melukis garis lurus biasa dan lengkung Bezier. Ini hanyalah lengkung biasa Perkara yang menarik tentang lengkung Bezier ialah ia boleh melukis lengkung tertutup, seperti sekeping kod ini
- Kod CSS
- Salin kandungan ke papan keratan
- g.beginPath();
 g.strokeStyle=
g.strokeStyle=
"#00F"
-

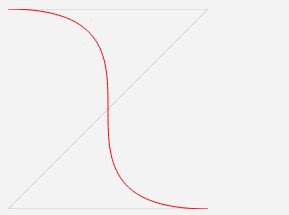
Tetapkan kedudukan permulaan dan penamat lengkung Bezier kubik ke titik yang sama untuk melukis lengkung tertutup. Oleh kerana arah interpolasi lengkung Bezier tidak mengikut paksi koordinat, lengkung tertutup boleh dilukis. Jika kita mahu interpolasi polinomial melukis lengkung tertutup, kita perlu menukar parameter dan menggunakan sistem koordinat kutub untuk melengkapkan.
Contoh yang saya gunakan adalah semua lengkung Bezier kubik. Sebenarnya, langkah kedua adalah sama, tetapi tanpa titik tengah, saya tidak dapat melukis apa yang saya mahu. Saya tidak akan meneruskan terlalu banyak, itu sahaja untuk artikel ini = =. .
 Apa yang dirujuk oleh H5? Meneroka konteksApr 12, 2025 am 12:03 AM
Apa yang dirujuk oleh H5? Meneroka konteksApr 12, 2025 am 12:03 AMH5referstohtml5, apivotaltechnologyinwebdevelopment.1) html5introducesnewelementsandapisforrich, dynamicwebapplications.2) itsupp ortsmultimediawithoutplugins, enhancusexperienceaceacrossdevices.3) SemantikelementsImproveContentstructureandseo.4) H5'srespo
 H5: Alat, Rangka Kerja, dan Amalan TerbaikApr 11, 2025 am 12:11 AM
H5: Alat, Rangka Kerja, dan Amalan TerbaikApr 11, 2025 am 12:11 AMAlat dan kerangka yang perlu dikuasai dalam pembangunan H5 termasuk Vue.js, React dan Webpack. 1.vue.js sesuai untuk membina antara muka pengguna dan menyokong pembangunan komponen. 2. Leact mengoptimumkan rendering halaman melalui DOM maya, sesuai untuk aplikasi yang kompleks. 3.WebPack digunakan untuk pembungkusan modul dan mengoptimumkan beban sumber.
 Warisan HTML5: Memahami H5 pada masa kiniApr 10, 2025 am 09:28 AM
Warisan HTML5: Memahami H5 pada masa kiniApr 10, 2025 am 09:28 AMHtml5hassignificlylylectransformedwebdevelopmentbyintroducingsemanticelements, enhancingmultimediasupport, andimprovingperformance.1) itmadewebebsitesmoreaccessibleandseo-friendlywithSemhyViVeShive, dan
 Kod H5: Kebolehcapaian dan HTML SemantikApr 09, 2025 am 12:05 AM
Kod H5: Kebolehcapaian dan HTML SemantikApr 09, 2025 am 12:05 AMH5 meningkatkan kebolehaksesan laman web dan kesan SEO melalui unsur -unsur semantik dan atribut ARIA. 1. Gunakan, dan lain -lain untuk mengatur struktur kandungan dan meningkatkan SEO. 2. Atribut Aria seperti ARIA-Label meningkatkan kebolehcapaian, dan pengguna teknologi bantuan boleh menggunakan laman web dengan lancar.
 Adakah H5 sama dengan HTML5?Apr 08, 2025 am 12:16 AM
Adakah H5 sama dengan HTML5?Apr 08, 2025 am 12:16 AM"H5" dan "HTML5" adalah sama dalam kebanyakan kes, tetapi mereka mungkin mempunyai makna yang berbeza dalam senario tertentu tertentu. 1. "HTML5" adalah standard yang ditentukan oleh W3C yang mengandungi tag dan API baru. 2. "H5" biasanya merupakan singkatan HTML5, tetapi dalam pembangunan mudah alih, ia boleh merujuk kepada rangka kerja berdasarkan HTML5. Memahami perbezaan ini membantu menggunakan istilah ini dengan tepat dalam projek anda.
 Apakah fungsi H5?Apr 07, 2025 am 12:10 AM
Apakah fungsi H5?Apr 07, 2025 am 12:10 AMH5, atau HTML5, adalah versi kelima HTML. Ia menyediakan pemaju dengan set alat yang lebih kuat, menjadikannya lebih mudah untuk membuat aplikasi web yang kompleks. Fungsi teras H5 termasuk: 1) unsur -unsur yang membolehkan lukisan grafik dan animasi di laman web; 2) tag semantik seperti, dan lain -lain untuk menjadikan struktur laman web jelas dan kondusif untuk pengoptimuman SEO; 3) API baru seperti perkhidmatan berasaskan lokasi GeolocationPi; 4) Keserasian silang penyemak imbas perlu dipastikan melalui ujian keserasian dan perpustakaan polyfill.
 Cara melakukan pautan h5Apr 06, 2025 pm 12:39 PM
Cara melakukan pautan h5Apr 06, 2025 pm 12:39 PMBagaimana untuk membuat pautan H5? Tentukan sasaran pautan: Dapatkan URL halaman atau aplikasi H5. Buat HTML Anchors: Gunakan & lt; a & gt; Tag untuk membuat sauh dan tentukan URL sasaran pautan. Tetapkan sifat pautan (pilihan): Tetapkan sasaran, tajuk, dan sifat onClick seperti yang diperlukan. Tambah ke laman web: Tambah kod utama HTML ke laman web di mana anda mahu pautan muncul.
 Cara menyelesaikan masalah keserasian H5Apr 06, 2025 pm 12:36 PM
Cara menyelesaikan masalah keserasian H5Apr 06, 2025 pm 12:36 PMPenyelesaian kepada isu keserasian H5 termasuk: menggunakan reka bentuk responsif yang membolehkan laman web menyesuaikan susun atur mengikut saiz skrin. Gunakan alat ujian silang penyemak imbas untuk menguji keserasian sebelum dilepaskan. Gunakan Polyfill untuk memberi sokongan untuk API baru untuk pelayar yang lebih tua. Ikuti piawaian web dan gunakan kod yang berkesan dan amalan terbaik. Gunakan preprocessors CSS untuk memudahkan kod CSS dan meningkatkan kebolehbacaan. Mengoptimumkan imej, mengurangkan saiz laman web dan mempercepatkan pemuatan. Dayakan HTTPS untuk memastikan keselamatan laman web.


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Dreamweaver CS6
Alat pembangunan web visual

SecLists
SecLists ialah rakan penguji keselamatan muktamad. Ia ialah koleksi pelbagai jenis senarai yang kerap digunakan semasa penilaian keselamatan, semuanya di satu tempat. SecLists membantu menjadikan ujian keselamatan lebih cekap dan produktif dengan menyediakan semua senarai yang mungkin diperlukan oleh penguji keselamatan dengan mudah. Jenis senarai termasuk nama pengguna, kata laluan, URL, muatan kabur, corak data sensitif, cangkerang web dan banyak lagi. Penguji hanya boleh menarik repositori ini ke mesin ujian baharu dan dia akan mempunyai akses kepada setiap jenis senarai yang dia perlukan.

PhpStorm versi Mac
Alat pembangunan bersepadu PHP profesional terkini (2018.2.1).

ZendStudio 13.5.1 Mac
Persekitaran pembangunan bersepadu PHP yang berkuasa

SublimeText3 Linux versi baharu
SublimeText3 Linux versi terkini





