Cara menggunakan tujuh kaedah pengisihan struktur data Java

1. Isih sisipan

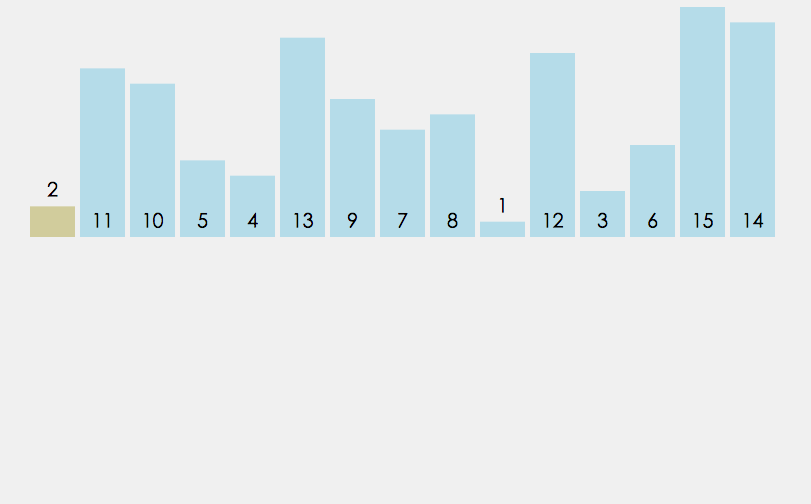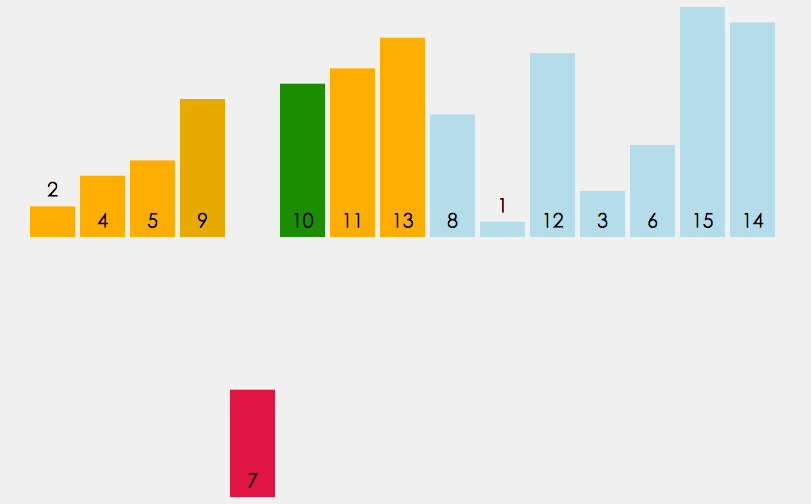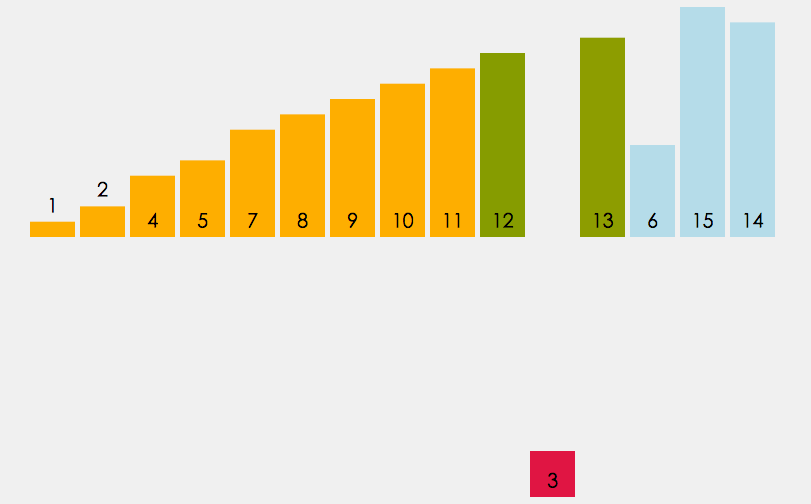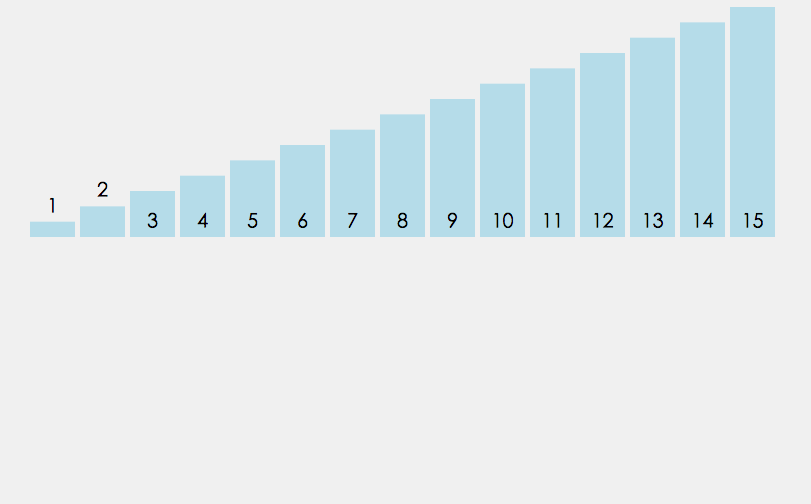
1. Tatasusunan[0], tatasusunan[1],..., tatasusunan[i-1] telah diisih pada masa ini, gunakan tatasusunan[i] dan tatasusunan[i-1], tatasusunan[i-2], ... Bandingkan, cari kedudukan sisipan, masukkan tatasusunan[i] dan gerakkan elemen pada kedudukan asal ke belakang.

Semakin dekat data untuk dipesan, semakin sedikit masa yang diambil untuk memasukkan isihan terus.

Kerumitan masa: O(N^2)

Kerumitan ruang O(1), iaitu algoritma yang stabil

Isihan sisipan langsung:

    public static void insertSort(int[] array){
        for (int i = 1; i < array.length; i++) {
            int tmp=array[i];
            int j=i-1;
            for(;j>=0;--j){
                if(array[j]>tmp){
                    array[j+1]=array[j];
                }else{
                    break;
                }
            }
            array[j+1]=tmp;
        }
    }

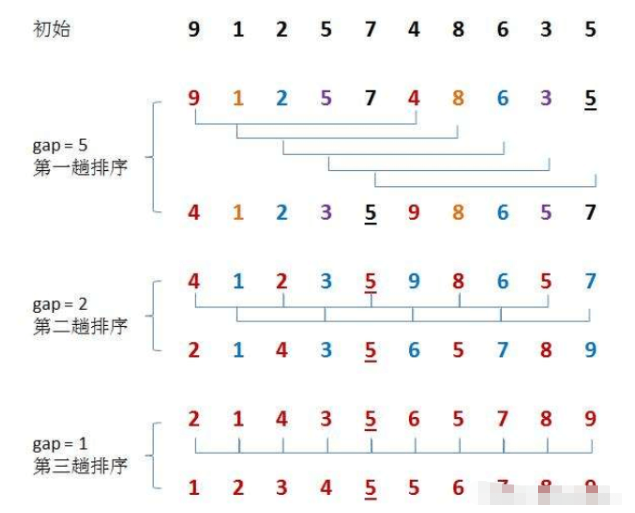
2. Isih bukit

Idea asas kaedah isihan Bukit ialah: mula-mula pilih jurang integer, dan bahagikan semua rekod dalam fail untuk diisih ke dalam kumpulan jurang , semua nombor dengan jarak jurang berada dalam kumpulan yang sama, dan nombor dalam setiap kumpulan terus dimasukkan dan diisih. Kemudian ambil gap=gap/2 dan ulangi kerja pengelompokan dan pengasingan di atas. Apabila gap=1, semua nombor diisih terus dalam kumpulan.

Isih bukit ialah pengoptimuman isihan sisipan langsung.
Tujuannya adalah untuk menjadikan tatasusunan lebih dekat kepada susunan, jadi pra-isih dilakukan apabila jurang > 1. Isih sisipan boleh mengisih tatasusunan yang hampir tersusun dengan cepat apabila jurangnya ialah 1.
Kerumitan masa pengisihan Bukit sukar dikira kerana terdapat banyak cara untuk mengira jurang, menjadikannya sukar untuk dikira.
Isih bukit:

public static void shellSort(int[] array){
        int size=array.length;
        //这里定义gap的初始值为数组长度的一半
        int gap=size/2;
        while(gap>0){
            //间隔为gap的直接插入排序
            for (int i = gap; i < size; i++) {
                int tmp=array[i];
                int j=i-gap;
                for(;j>=0;j-=gap){
                    if(array[j]>tmp){
                        array[j+gap]=array[j];
                    }else{
                        break;
                    }
                }
                array[j+gap]=tmp;
            }
            gap/=2;
        }
    }

2. Isih pilihan

1 >

Pilih elemen data terkecil

• dalam tatasusunan set elemen[i]--array[n-1] jika ia bukan elemen pertama dalam set ini daripada elemen satu, kemudian tukarkannya dengan elemen pertama dalam set elemen ini

• Dalam set yang tinggal, ulangi langkah di atas sehingga terdapat 1 elemen yang tinggal dalam set

• Kerumitan masa: O(N^2)

Kerumitan ruang ialah O(1), tidak stabil

Isih pilihan:

    //交换
    private static void swap(int[] array,int i,int j){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }
    //选择排序
    public static void chooseSort(int[] array){
        for (int i = 0; i < array.length; i++) {
            int minIndex=i;//记录最小值的下标
            for (int j = i+1; j < array.length; j++) {
                if (array[j]<array[minIndex]) {
                    minIndex=j;
                }
            }
            swap(array,i,minIndex);
        }
    }

2. Isih timbunan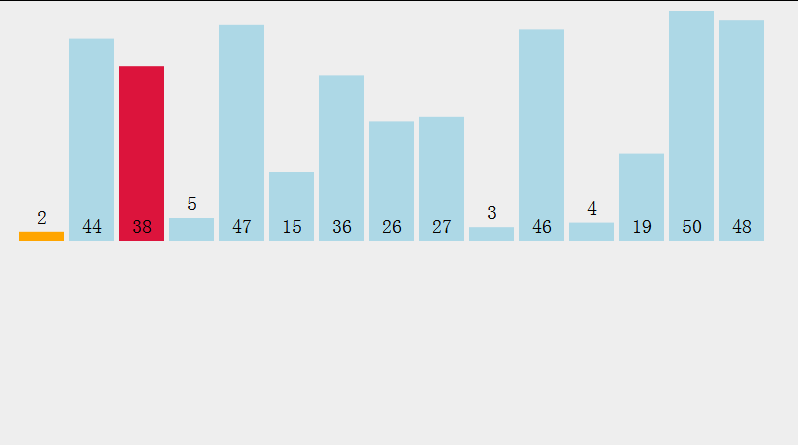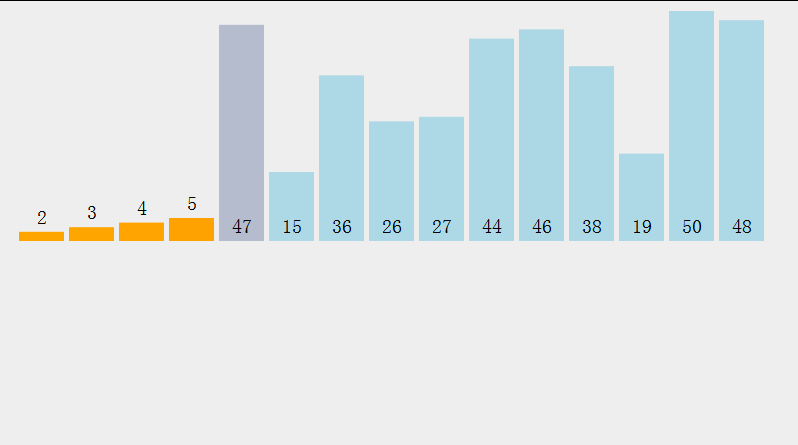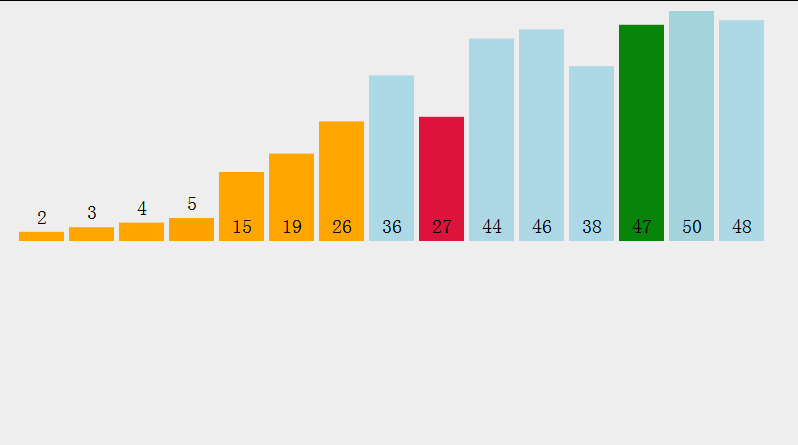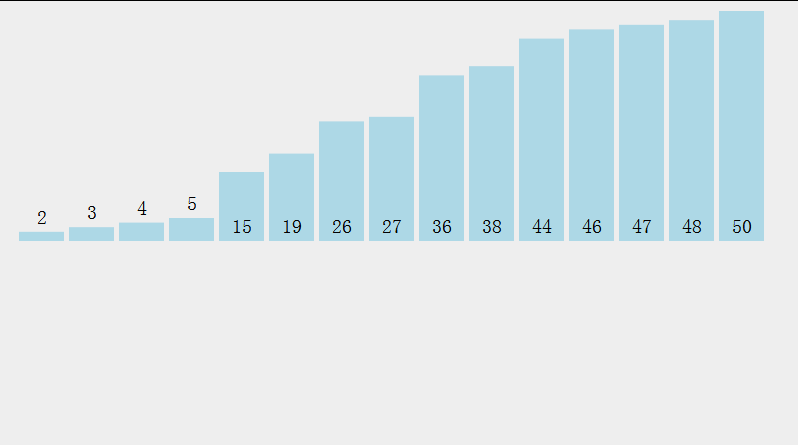

Dua idea isihan timbunan (mengambil contoh tertib menaik):

Buat timbunan akar kecil, dalam perintah Keluarkan elemen atas timbunan dan masukkan ke dalam tatasusunan sehingga timbunan kosong

• Buat timbunan akar yang besar, tentukan kunci kedudukan elemen ekor timbunan dan tukar elemen atas timbunan dan elemen pada kedudukan kunci setiap kali (kunci --), sehingga kunci mencapai bahagian atas timbunan Pada masa ini, melintasi elemen dalam timbunan adalah dalam tertib menaik (seperti berikut)

• Kerumitan masa: O(N^2)

Kerumitan ruang: O(N), tidak stabil

Isihan timbunan:

    //向下调整
    public static void shiftDown(int[] array,int parent,int len){
        int child=parent*2+1;
        while(child<len){
            if(child+1<len){
                if(array[child+1]>array[child]){
                    child++;
                }
            }
            if(array[child]>array[parent]){
                swap(array,child,parent);
                parent=child;
                child=parent*2+1;
            }else{
                break;
            }
 
        }
    }
    //创建大根堆
    private static void createHeap(int[] array){
        for (int parent = (array.length-1-1)/2; parent >=0; parent--) {
            shiftDown(array,parent,array.length);
        }
    }
    //堆排序
    public static void heapSort(int[] array){
        //创建大根堆
        createHeap(array);
        //排序
        for (int i = array.length-1; i >0; i--) {
            swap(array,0,i);
            shiftDown(array,0,i);
        }
    }

3. Isih pertukaran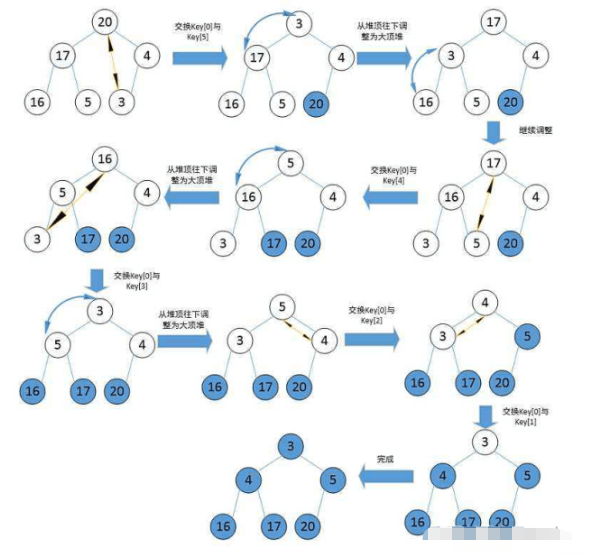

1 , Isih gelembung

Gelung dua peringkat, gelung peringkat pertama mewakili bilangan kali diisih dan gelung peringkat kedua mewakili bilangan perbandingan yang akan dibuat dalam setiap pas; pengisihan gelembung di sini telah dioptimumkan, dan dalam setiap pas Apabila membandingkan, kita boleh menentukan pembilang untuk merekodkan bilangan pertukaran data , ini bermakna bahawa data sudah teratur dan tiada pengisihan selanjutnya diperlukan.

Kerumitan masa: O(N^2)

Kerumitan ruang ialah O(1), iaitu jenis yang stabil

Isih buih:

   public static void bubbleSort(int[] array){
        for(int i=0;i<array.length-1;++i){
            int count=0;
            for (int j = 0; j < array.length-1-i; j++) {
                if(array[j]>array[j+1]){
                    swap(array,j,j+1);
                    count++;
                }
            }
            if(count==0){
                break;
            }
        }
    }

2. Isih pantas

Ambil sebarang elemen dalam jujukan elemen untuk diisih sebagai nilai rujukan, dan bahagikan set untuk diisih kepada dua jujukan mengikut kod isihan .

Kerumitan masa: sebaik-baiknya o (n*logn): setiap kali urutan yang hendak diisih boleh dibahagikan sama rata

O (n^2) yang paling teruk): Urutan susunan ialah susunan itu sendiri Tertib

kerumitan ruang: terbaik O(logn), paling teruk O(N). Pengisihan tidak stabil

(1) Kaedah penggalian

Apabila data dipesan, pengisihan pantas adalah bersamaan dengan pokok binari tanpa subpokok kiri atau kanan, dan kerumitan ruang akan mencapai O(N), jika sejumlah besar data diisih, ia boleh menyebabkan limpahan tindanan.

public static void quickSort(int[] array,int left,int right){
        if(left>=right){
            return;
        }
        int l=left;
        int r=right;
        int tmp=array[l];
        while(l<r){
            while(array[r]>=tmp&&l<r){
            //等号不能省略，如果省略，当序列中存在相同的值时，程序会死循环
                r--;
            }
            array[l]=array[r];
            while(array[l]<=tmp&&l<r){
                l++;
            }
            array[r]=array[l];
        }
        array[l]=tmp;
        quickSort(array,0,l-1);
        quickSort(array,l+1,right);
    }

(2) Pengoptimuman isihan pantas

Tiga nombor untuk memilih kunci

Berkenaan pemilihan nilai kunci, jika urutan yang hendak diisih adalah teratur, maka kami Memilih kekunci pertama atau terakhir sebagai kunci boleh menyebabkan bahagian kiri atau kanan pemisahan menjadi kosong Dalam kes ini, kerumitan ruang isihan pantas akan menjadi agak besar dan ia mudah menyebabkan limpahan timbunan. Kemudian kita boleh menggunakan kaedah tiga nombor untuk membatalkan keadaan ini. Nilai tengah unsur pertama, terakhir dan tengah dalam jujukan digunakan sebagai nilai utama.

 //key值的优化，只在快速排序中使用，则可以为private
    private int threeMid(int[] array,int left,int right){
        int mid=(left+right)/2;
        if(array[left]>array[right]){
            if(array[mid]>array[left]){
                return left;
            }
            return array[mid]<array[right]?right:mid;
        }else{
            if(array[mid]<array[left]){
                return left;
            }
            return array[mid]>array[right]?right:mid;
        }
    }

Apabila mengulangi ke subjulat kecil, anda boleh mempertimbangkan untuk menggunakan isihan sisipan

随着我们递归的进行，区间会变的越来越小，我们可以在区间小到一个值的时候，对其进行插入排序，这样代码的效率会提高很多。

（3）快速排序的非递归实现

 //找到一次划分的下标
    public static int patition(int[] array,int left,int right){
        int tmp=array[left];
        while(left<right){
            while(left<right&&array[right]>=tmp){
                right--;
            }
            array[left]=array[right];
            while(left<right&&array[left]<=tmp){
                left++;
            }
            array[right]=array[left];
        }
        array[left]=tmp;
        return left;
    }
    //快速排序的非递归
    public static void quickSort2(int[] array){
        Stack<Integer> stack=new Stack<>();
        int left=0;
        int right=array.length-1;
        stack.push(left);
        stack.push(right);
        while(!stack.isEmpty()){
            int r=stack.pop();
            int l=stack.pop();
            int p=patition(array,l,r);
            if(p-1>l){
                stack.push(l);
                stack.push(p-1);
            }
            if(p+1<r){
                stack.push(p+1);
                stack.push(r);
            }
        }
    }

四、归并排序

归并排序（MERGE-SORT）：该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。实现序列的完全有序，需要将已经有序的子序列合并，即先让每个子序列有序，然后再将相邻的子序列段有序。若将两个有序表合并成一个有序表，称为二路归并。

时间复杂度：O(n*logN)（无论有序还是无序）

空间复杂度：O（N）。是稳定的排序。

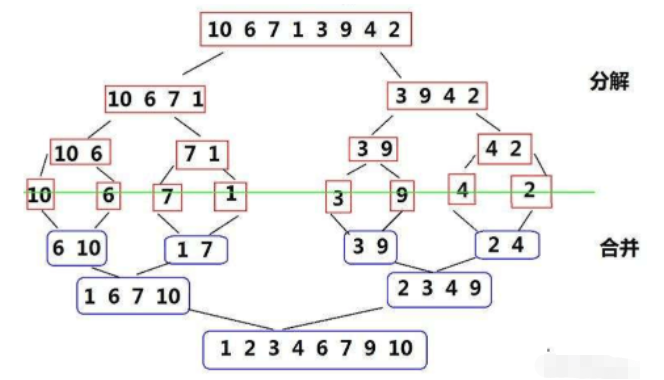
    //归并排序：递归
    public static void mergeSort(int[] array,int left,int right){
        if(left>=right){
            return;
        }
        int mid=(left+right)/2;
        //递归分割
        mergeSort(array,left,mid);
        mergeSort(array,mid+1,right);
        //合并
        merge(array,left,right，mid);
    }
    //非递归
    public static void mergeSort1(int[] array){
        int gap=1;
        while(gap<array.length){
            for (int i = 0; i < array.length; i+=2*gap) {
                int left=i;
                int mid=left+gap-1;
                if(mid>=array.length){
                    mid=array.length-1;
                }
                int right=left+2*gap-1;
                if(right>=array.length){
                    right=array.length-1;
                }
                merge(array,left,right,mid);
            }
            gap=gap*2;
        }
    } 
    //合并：合并两个有序数组
    public static void merge(int[] array,int left,int right，int mid){
        int[] tmp=new int[right-left+1];
        int k=0;
        int s1=left;
        int e1=mid;
        int s2=mid+1;
        int e2=right;
        while(s1<=e1&&s2<=e2){
            if(array[s1]<=array[s2]){
                tmp[k++]=array[s1++];
            }else{
                tmp[k++]=array[s2++];
            }
        }
        while(s1<=e1){
            tmp[k++]=array[s1++];
        }
        while(s2<=e2){
            tmp[k++]=array[s2++];
        }
        for (int i = left; i <= right; i++) {
            array[i]=tmp[i-left];
        }
    }

五、排序算法的分析

排序方法	最好时间复杂度	最坏时间复杂度	空间复杂度	稳定性
直接插入排序	O(n)	O(n^2)	O(1)	稳定
希尔排序	O(n)	O(n^2)	O(1）	不稳定
直接排序	O(n^2)	O(n^2)	O(1)	不稳定
堆排序	O(nlog(2)n)	O(nlog(2)n)	O(1)	不稳定
冒泡排序	O(n)	O(n^2)	O(1)	稳定
快速排序	O(nlog(2)n)	O(n^2)	O(nlog(2)n)	不稳定
归并排序	O(nlog(2)n)	O(nlog(2)n)	O(n)	稳定

Atas ialah kandungan terperinci Cara menggunakan tujuh kaedah pengisihan struktur data Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!