Apakah rangka kerja pengumpulan dan algoritma biasa struktur data Java?

1 Rangka Kerja Koleksi

1.1 Konsep Rangka Kerja Koleksi

Rangka Kerja Koleksi Java Rangka Kerja Koleksi Java, juga dikenali sebagai bekas kontena, ialah definisi Satu set antara muka dan kelas pelaksanaannya di bawah pakej java.util.

Prestasi utamanya ialah meletakkan berbilang elemen dalam satu unit, yang digunakan untuk menyimpan, mendapatkan semula dan mengurus elemen ini dengan cepat dan mudah, yang biasanya dikenali sebagai CRUD.

Ikhtisar kelas dan antara muka:

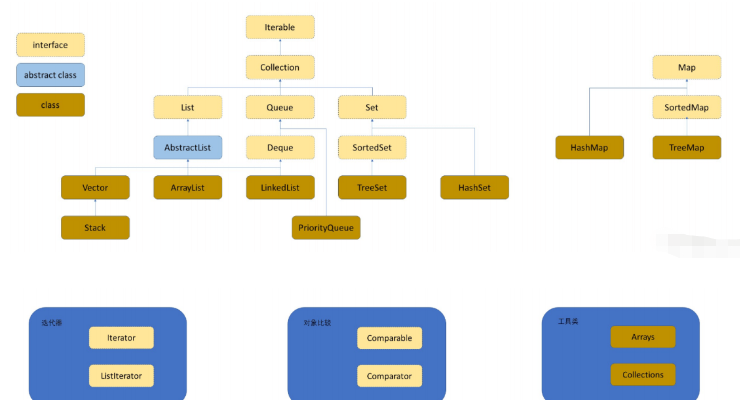
1.2 Struktur data yang terlibat dalam bekas

Koleksi: ialah antara muka yang mengandungi bekas yang paling biasa digunakan Beberapa kaedah

Senarai: ialah antara muka yang menyeragamkan kaedah yang akan dilaksanakan dalam ArrayList dan LinkedList

• ArrayList: melaksanakan antara muka Senarai, dan lapisan bawah ialah jadual jujukan jenis dinamik

• LinkedList: melaksanakan antara muka Senarai dan lapisan bawah ialah senarai terpaut dua hala

Timbunan: bahagian bawah lapisan ialah tindanan, iaitu senarai jujukan khas

Baris gilir: Lapisan bawah ialah baris gilir, iaitu jadual jujukan khas

Deque: Ia adalah antara muka

Set: Set, ia ialah antara muka dan model K diletakkan di dalamnya

• HashSet: Lapisan bawah ialah baldi cincang, dan kerumitan masa pertanyaan ialah O(1 )

• TreeSet: Lapisan bawah ialah pokok merah-hitam, Kerumitan masa pertanyaan ialah O(), berkenaan urutan kunci

Peta: pemetaan, yang menyimpan pasangan nilai kunci model K-V

• HashMap: Lapisan bawah ialah baldi cincang dan kerumitan masa pertanyaan ialah O(1)

• TreeMap: Lapisan bawah ialah pokok merah-hitam, dan kerumitan masa pertanyaan ialah O(), Perihal susunan kunci

2 Algoritma

2.1 Konsep Algoritma

Algoritma: Ia adalah proses pengiraan yang jelas Ia memerlukan satu atau satu Kumpulan nilai dimasukkan dan menghasilkan nilai atau kumpulan nilai sebagai keluaran. Algoritma ialah satu siri langkah pengiraan yang direka untuk mengubah data input kepada hasil output.

2.2 Kecekapan algoritma

Analisis kecekapan algoritma dibahagikan kepada dua jenis: yang pertama ialah kecekapan masa, dan yang kedua ialah kecekapan ruang. Kecekapan masa dipanggil kerumitan masa, manakala kecekapan ruang dipanggil kerumitan ruang. Kerumitan masa terutamanya mengukur kelajuan berjalan algoritma, manakala kerumitan ruang terutamanya mengukur ruang tambahan yang diperlukan oleh algoritma Pada hari-hari awal pembangunan komputer, kapasiti penyimpanan komputer adalah sangat kecil. Jadi kami sangat mengambil berat tentang kerumitan ruang. Dengan perkembangan pesat industri komputer, kapasiti penyimpanan komputer telah mencapai tahap yang sangat tinggi. Jadi kita tidak perlu lagi memberi perhatian khusus kepada kerumitan ruang sesuatu algoritma.

3 Kerumitan Masa

3.1 Konsep Kerumitan Masa

Kerumitan masa ialah fungsi matematik dalam sains komputer yang mewakili masa berjalan sesuatu algoritma dan secara kuantitatif menerangkan kecekapan masa algoritma . Adalah mustahil untuk mengira masa pelaksanaan algoritma secara teori Masa yang memakan masa hanya boleh diketahui selepas program benar-benar dijalankan pada komputer. Walaupun setiap algoritma boleh diuji pada komputer, ini sangat menyusahkan, jadi ada cara untuk menganalisisnya melalui kerumitan masa. Kerumitan masa bagi sesuatu algoritma adalah berkadar dengan masa yang diperlukan untuk melaksanakan pernyataan, dan kerumitan masa bergantung pada bilangan pelaksanaan operasi asas dalam algoritma.

3.2 Notasi asimptotik O Big

// 请计算一下func1基本操作执行了多少次？
void func1(int N){
	int count = 0;
	for (int i = 0; i < N ; i++) {
		for (int j = 0; j < N ; j++) {
			count++;
		}
	}
	for (int k = 0; k < 2 * N ; k++) {
		count++;
	} 
	int M = 10;
	while ((M--) > 0) {
		count++;
	} 
	System.out.println(count);
}

Bilangan operasi asas yang dilakukan oleh Func1: F(N)=N^2+2*N+10

• N = 10 F(N) = 130

• N = 100 F(N) = 10210

• N = 1000 F( N) = 1002010

Malah, apabila kita mengira kerumitan masa, kita sebenarnya tidak perlu mengira bilangan eksekusi yang tepat, tetapi hanya anggaran bilangan pelaksanaan, jadi di sini kami menggunakan Big O perwakilan progresif .

Notasi O Besar: Ia ialah tatatanda matematik yang digunakan untuk menerangkan kelakuan asimptotik bagi suatu fungsi

3.3 Terbitan kaedah tertib O Besar

• Digunakan Pemalar 1 menggantikan semua pemalar aditif dalam masa jalan.

• Dalam bilangan fungsi larian yang diubah suai, hanya istilah tertib tertinggi dikekalkan.

• Jika sebutan tertib tertinggi hadir dan bukan 1, keluarkan pemalar yang didarab dengan sebutan ini. Hasilnya ialah pesanan Big O.

Selepas menggunakan perwakilan asimptotik O besar, kerumitan masa Func1 ialah: O(n^2)

• N = 10 F (N) = 100

• N = 100 F(N) = 10000

• N = 1000 F(N) = 1000000

Melalui kandungan di atas, kita dapat melihat bahawa notasi asimptotik Big O mengecualikan item yang mempunyai sedikit impak pada hasilnya, sekali gus menyatakan bilangan pelaksanaan secara ringkas dan jelas. Selain itu, kerumitan masa beberapa algoritma mempunyai kes terbaik, purata dan terburuk:

Kes terburuk: bilangan maksimum larian (batas atas) untuk sebarang saiz input

Kes purata: sebarang input saiz Jumlah jangkaan larian

Kes terbaik: bilangan minimum larian (batas bawah) untuk sebarang saiz input

Contohnya: mencari data x

dalam susunan panjang N Kes yang baik: 1 kali ditemui

Kes terburuk: N kali ditemui

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

4 空间复杂度

对于一个算法而言，空间复杂度表示它在执行期间所需的临时存储空间大小。空间复杂度的计算方式并非程序所占用的字节数量，因为这并没有太大的意义；实际上，空间复杂度的计算基于变量的数量。大O渐进表示法通常用来计算空间复杂度，其计算规则类似于实践复杂度的计算规则。

实例1:

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {
	for (int end = array.length; end > 0; end--) {
		boolean sorted = true;
		for (int i = 1; i < end; i++) {
			if (array[i - 1] > array[i]) {
				Swap(array, i - 1, i);
				sorted = false;
			}
		} 
		if(sorted == true) {
		break;
		}
	}
}

实例2:

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {
	long[] fibArray = new long[n + 1];
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; i++) {
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
	} 
	return fibArray;
}

实例3:

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
	return N < 2 ? N : factorial(N-1)*N;
}

• 实例1使用了常数个额外空间，所以空间复杂度为 O(1)

• 实例2动态开辟了N个空间，空间复杂度为 O(N)

• 实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

Atas ialah kandungan terperinci Apakah rangka kerja pengumpulan dan algoritma biasa struktur data Java?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!