Cara menggunakan operasi bitwise untuk melaksanakan pendaraban dalam Java

Pendaraban perpuluhan

Sebagai contoh, 26 * 15, apabila melakukan operasi pendaraban, biasanya kita mengiranya seperti ini, mula-mula darab 5 dengan 6 untuk mendapatkan 30, tulis 0 Letakkan 3 ketepikan, kemudian darab 5 dengan 2 untuk mendapatkan 10, tambahkan 3 sebelumnya dan tulis di bawah untuk mendapatkan 130; selepas mengira 5, kira 1 masing-masing Darab 6 dan 2 dan rekodkan keputusan 26 di bawah, kemudian tambah 130 dan 26 (dengan terkehel) untuk mendapatkan 390.

Pendaraban binari

Selepas membaca pendaraban perpuluhan, mari kita lihat pendaraban binari Prinsip asasnya adalah sama, dan ia juga didarab dengan a silang. Contohnya, hitung 5 * 7. Sistem perduaan bagi

5 ialah 101, dan sistem perduaan bagi 7 ialah 111 Mari kita lihat kaedah pendaraban silang binari.

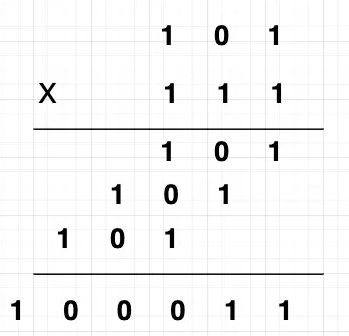
Anda boleh melihat bahawa binari adalah 101 dan binari 111 dikira dengan cara tradisional, dan hasilnya adalah 100011, manakala binari 100011 sepadan kepada Perpuluhan ialah 35.
Jadi, dalam proses pengiraan, kaedah pengiraan perpuluhan dan binari adalah sama, contoh dan bukti tidak akan diberikan di sini.

Analisis Idea

Sekarang proses pengiraan sudah ada, bagaimana untuk melaksanakannya dengan kod?

Mari kita lihat proses pengiraan binari dalam gambar di atas:

• Darab pertama digit terakhir 111 perduaan 1 dengan 101 untuk mendapatkan101.

• kemudian didarab dengan digit terakhir kedua 111 perduaan 1 dengan 101 untuk mendapatkan 101.

• kemudian didarab dengan digit terakhir ketiga 111 perduaan 1 dengan 101 untuk mendapatkan 101. Tiga

  s yang diperolehi oleh

• 101 ditambah dalam binari untuk mendapatkan 100011.

Perhatikan bahawa keputusan 2 yang diperoleh dalam langkah 3 dan langkah 101 kedua-duanya digerakkan ke hadapan satu tempat, yang bersamaan dengan 1010 dan 10100, juga Pengiraan akhir ialah: 10100 + 1010 + 101 = 100011.

Mari kita lihat pengiraan penambahan akhir10100 + 1010 + 101 = 100011, iaitu, selagi kita mencari cara untuk menukar data kepada penambahan beberapa digit, kerana kita telah pun menyedari cara menggunakan operasi bit untuk melaksanakan operasi tambah.

Nombor ketiga-tiga nombor ini 101, 1010 dan 10100 adalah betul-betul sama dengan nombor perduaan 111, iaitu berapa banyak nombor perduaan (pengganda 111 di bahagian bawah gambar di atas) ialah Bit akan menghasilkan penambahan beberapa nombor Jika didarab dengan 11111, penambahan 5 nombor akan dihasilkan.

Mari kita lihat hubungan sebelum data:

• Hasil pendaraban pertama: 101 = 101 + 0

• Kali kedua Hasil pendaraban: 1111 = 101

• Hasil pendaraban ketiga: 100011 = 101

Dari sini kita dapat melihat bahawa setiap pengiraan Sekali, 101 hanya perlu beralih ke kiri sekali dan menambah hasil pengiraan terakhir.

Jadi, bagaimana anda tahu berapa kali beralih ke kiri? Daripada contoh di sini, selepas setiap pengiraan, 111 bergerak ke kanan sekali, dan 101 juga bergerak ke kiri sekali Sehingga 111 hanya tinggal digit terakhir, kemudian berhenti mengira.

Pelaksanaan kod

Mengikut idea di atas, laksanakan kod:

// 用位运算实现加法
public static int add(int a, int b) {
    int sum = 0;
    while (b != 0) {
        sum = a ^ b;
        b = (a & b) << 1;
        a = sum;
    }
    return sum;
}

// 用位运算实现减法
public static int multi(int a, int b) {
    int res = 0;
    while (b != 0) {
        if ((b & 1) != 0) {
            res = add(res, a);
        }
        a <<= 1;
        b >>>= 1;
    }
    return res;
}

Jalankan kod dan lihat hasilnya:

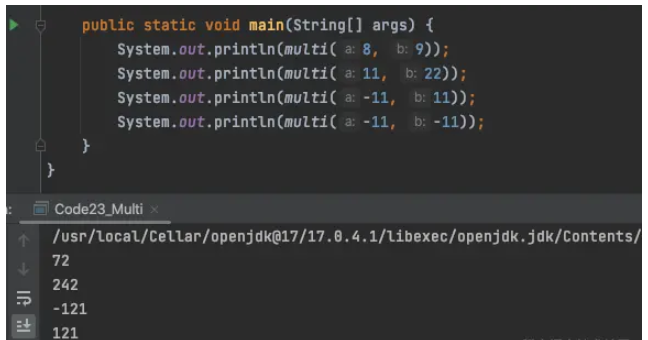
Anda dapat melihat bahawa pengiraan adalah betul dan nombor negatif juga disokong.

Atas ialah kandungan terperinci Cara menggunakan operasi bitwise untuk melaksanakan pendaraban dalam Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!