Rumah >pembangunan bahagian belakang >Tutorial Python >Strategi perdagangan dan analisis portfolio menggunakan Python
Strategi perdagangan dan analisis portfolio menggunakan Python
- 王林ke hadapan
- 2023-05-18 13:13:061926semak imbas
Kami akan mengukur prestasi strategi perdagangan dalam artikel ini. Dan akan membangunkan strategi dagangan momentum mudah yang akan menggunakan empat kelas aset: bon, saham dan hartanah. Kelas aset ini mempunyai korelasi yang rendah, yang menjadikannya pilihan pengimbangan risiko yang sangat baik.

Strategi Perdagangan Momentum
Strategi ini berdasarkan momentum kerana peniaga dan pelabur telah lama menyedari kesan momentum, yang boleh dilihat dalam pelbagai pasaran dan jangka masa seperti yang dilihat. Jadi kami memanggilnya sebagai strategi momentum. Mengikut aliran atau momentum siri masa (TSM) ialah nama lain untuk menggunakan strategi ini pada satu instrumen. Kami akan mencipta strategi momentum asas dan mengujinya pada TCS untuk melihat prestasinya.
Analisis Strategi TSM
Pertama, kami akan mengimport beberapa perpustakaan
import numpy as np import pandas as pd import matplotlib.pyplot as plt import yfinance as yf import ffn %matplotlib inline
Kami membina fungsi strategi momentum asas TSMStrategy. Fungsi ini akan mengembalikan prestasi yang dijangkakan melalui pulangan logaritma siri masa, tempoh masa minat dan pembolehubah Boolean untuk sama ada pintasan dibenarkan. Output fungsi
def TSMStrategy(returns, period=1, shorts=False):
if shorts:
position = returns.rolling(period).mean().map(
lambda x: -1 if x <= 0 else 1)
else:
position = returns.rolling(period).mean().map(
lambda x: 0 if x <= 0 else 1)
performance = position.shift(1) * returns
return performance
ticker = 'TCS'
yftcs = yf.Ticker(ticker)
data = yftcs.history(start='2005-01-01', end='2021-12-31')
returns = np.log(data['Close'] / data['Close'].shift(1)).dropna()
performance = TSMStrategy(returns, period=1, shorts=False).dropna()
years = (performance.index.max() - performance.index.min()).days / 365
perf_cum = np.exp(performance.cumsum())
tot = perf_cum[-1] - 1
ann = perf_cum[-1] ** (1 / years) - 1
vol = performance.std() * np.sqrt(252)
rfr = 0.02
sharpe = (ann - rfr) / vol
print(f"1-day TSM Strategy yields:" +
f"nt{tot*100:.2f}% total returns" +
f"nt{ann*100:.2f}% annual returns" +
f"nt{sharpe:.2f} Sharpe Ratio")
tcs_ret = np.exp(returns.cumsum())
b_tot = tcs_ret[-1] - 1
b_ann = tcs_ret[-1] ** (1 / years) - 1
b_vol = returns.std() * np.sqrt(252)
b_sharpe = (b_ann - rfr) / b_vol
print(f"Baseline Buy-and-Hold Strategy yields:" +
f"nt{b_tot*100:.2f}% total returns" +
f"nt{b_ann*100:.2f}% annual returns" +
f"nt{b_sharpe:.2f} Sharpe Ratio")adalah seperti berikut:
1-day TSM Strategy yields: -45.15% total returns -7.10% annual returns -0.17 Sharpe Ratio Baseline Buy-and-Hold Strategy yields: -70.15% total returns -13.78% annual returns -0.22 Sharpe Ratio
Dari segi pulangan tahunan yang munasabah, strategi TSM 1 hari adalah lebih baik daripada strategi beli dan tahan. Oleh kerana tinjauan balik 1 hari boleh mengandungi banyak aliran palsu, kami mencuba tempoh masa yang berbeza untuk melihat perbandingannya. Di sini model akan dijalankan dalam gelung selama 3, 5, 15, 30 dan 90 hari.
import matplotlib.gridspec as gridspec
periods = [3, 5, 15, 30, 90]
fig = plt.figure(figsize=(12, 10))
gs = fig.add_gridspec(4, 4)
ax0 = fig.add_subplot(gs[:2, :4])
ax1 = fig.add_subplot(gs[2:, :2])
ax2 = fig.add_subplot(gs[2:, 2:])
ax0.plot((np.exp(returns.cumsum()) - 1) * 100, label=ticker, linestyle='-')
perf_dict = {'tot_ret': {'buy_and_hold': (np.exp(returns.sum()) - 1)}}
perf_dict['ann_ret'] = {'buy_and_hold': b_ann}
perf_dict['sharpe'] = {'buy_and_hold': b_sharpe}
for p in periods:
log_perf = TSMStrategy(returns, period=p, shorts=False)
perf = np.exp(log_perf.cumsum())
perf_dict['tot_ret'][p] = (perf[-1] - 1)
ann = (perf[-1] ** (1/years) - 1)
perf_dict['ann_ret'][p] = ann
vol = log_perf.std() * np.sqrt(252)
perf_dict['sharpe'][p] = (ann - rfr) / vol
ax0.plot((perf - 1) * 100, label=f'{p}-Day Mean')
ax0.set_ylabel('Returns (%)')
ax0.set_xlabel('Date')
ax0.set_title('Cumulative Returns')
ax0.grid()
ax0.legend()
_ = [ax1.bar(i, v * 100) for i, v in enumerate(perf_dict['ann_ret'].values())]
ax1.set_xticks([i for i, k in enumerate(perf_dict['ann_ret'])])
ax1.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['ann_ret'].keys()],
rotation=45)
ax1.grid()
ax1.set_ylabel('Returns (%)')
ax1.set_xlabel('Strategy')
ax1.set_title('Annual Returns')
_ = [ax2.bar(i, v) for i, v in enumerate(perf_dict['sharpe'].values())]
ax2.set_xticks([i for i, k in enumerate(perf_dict['sharpe'])])
ax2.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['sharpe'].keys()],
rotation=45)
ax2.grid()
ax2.set_ylabel('Sharpe Ratio')
ax2.set_xlabel('Strategy')
ax2.set_title('Sharpe Ratio')
plt.tight_layout()
plt.show()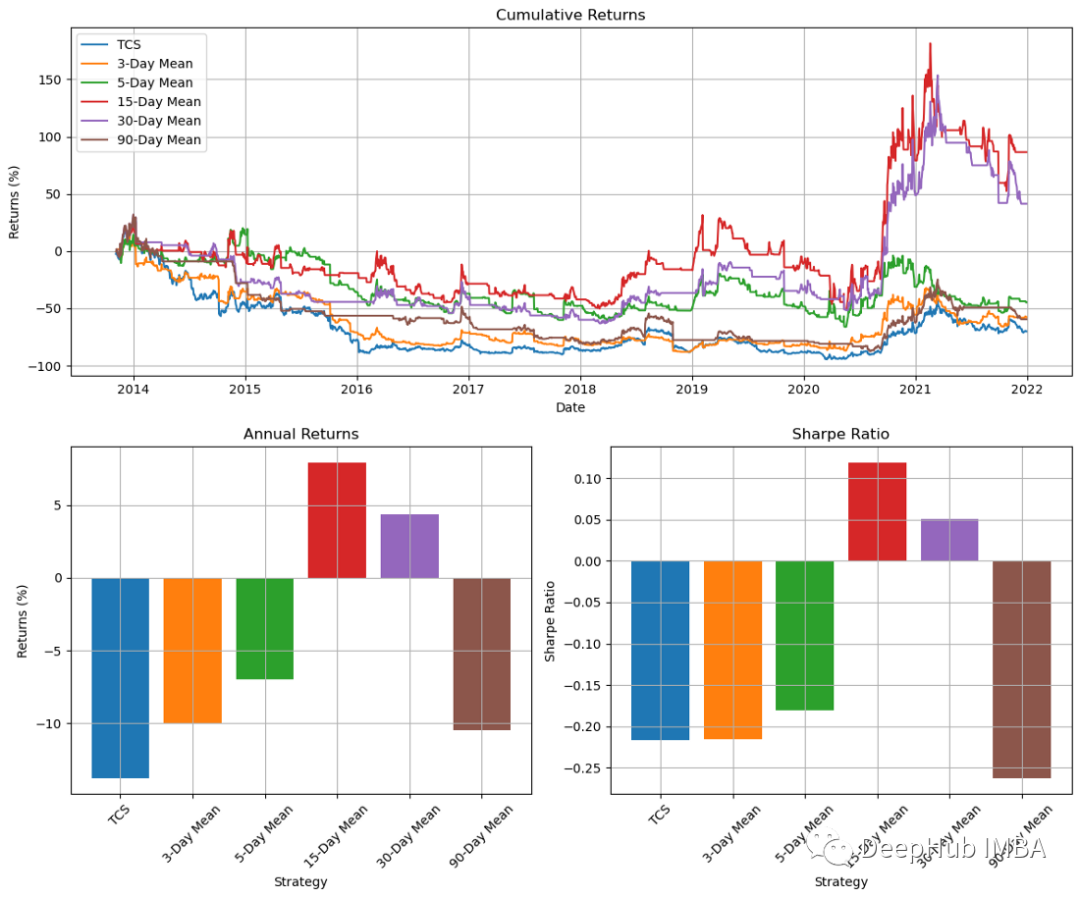
Melihat kepada keputusan pada carta, kita dapat melihat bahawa penunjuk momentum 15 hari memberikan hasil yang terbaik. Walau bagaimanapun, keputusan untuk tempoh masa lain adalah bercampur-campur. Ini menunjukkan bahawa strategi kami tidak boleh dipercayai. Jadi kita juga boleh keluar dari dagangan dengan menggunakan hentian atau trailing stop berhampiran bahagian atas, dan bukannya melakukannya apabila carta 15 hari turun atau mendatar.
Analisis Portfolio
Setakat ini kami telah mencipta strategi dagangan dalam Python. Di bawah ini kami akan mengukur dan memplotkan ciri portfolio biasa untuk memudahkan pemerhatian dan analisis kami.
Analisis Portfolio
Pertama, kami akan mengimport beberapa perpustakaan penting dan memerhatikan pelaksanaan data.
import pandas_datareader.data as web stocks = ['SPY','GLD','TLT','HYG'] data = web.DataReader(stocks,data_source='yahoo',start='01/01/2019')['Adj Close'] data.sort_index(ascending=True,inplace=True) perf = data.calc_stats() perf.plot()
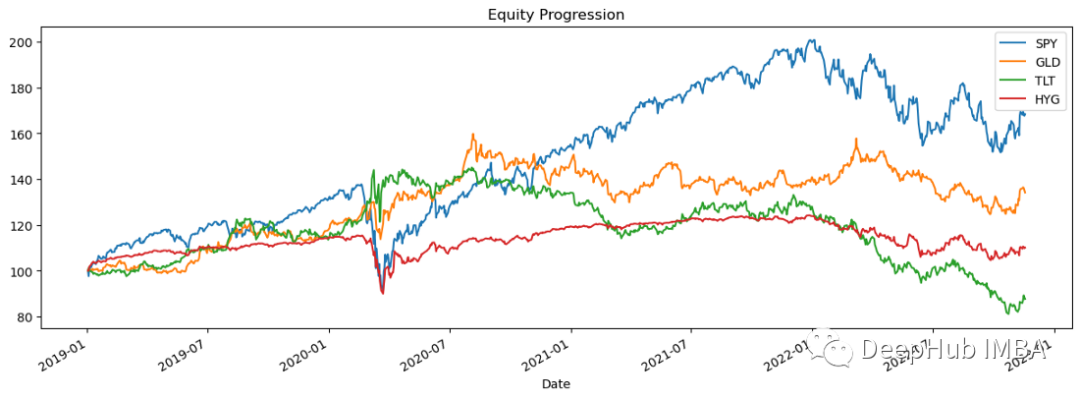
Pulangan log
Pulangan log digunakan untuk mengira kadar pertumbuhan eksponen. Daripada mengira peratusan perubahan harga untuk setiap sub-tempoh, kami mengira indeks pertumbuhan organik untuk tempoh tersebut. Mula-mula buat df yang mengandungi pulangan log setiap harga saham dalam data, kemudian kami cipta histogram untuk setiap pulangan log.
returns = data.to_log_returns().dropna() print(returns.head()) Symbols SPY GLD TLT HYG Date 2019-01-03 -0.024152 0.009025 0.011315 0.000494 2019-01-04 0.032947 -0.008119 -0.011642 0.016644 2019-01-07 0.007854 0.003453 -0.002953 0.009663 2019-01-08 0.009351 -0.002712 -0.002631 0.006470 2019-01-09 0.004663 0.006398 -0.001566 0.001193
Histogram adalah seperti berikut:
ax = returns.hist(figsize=(20, 10),bins=30)
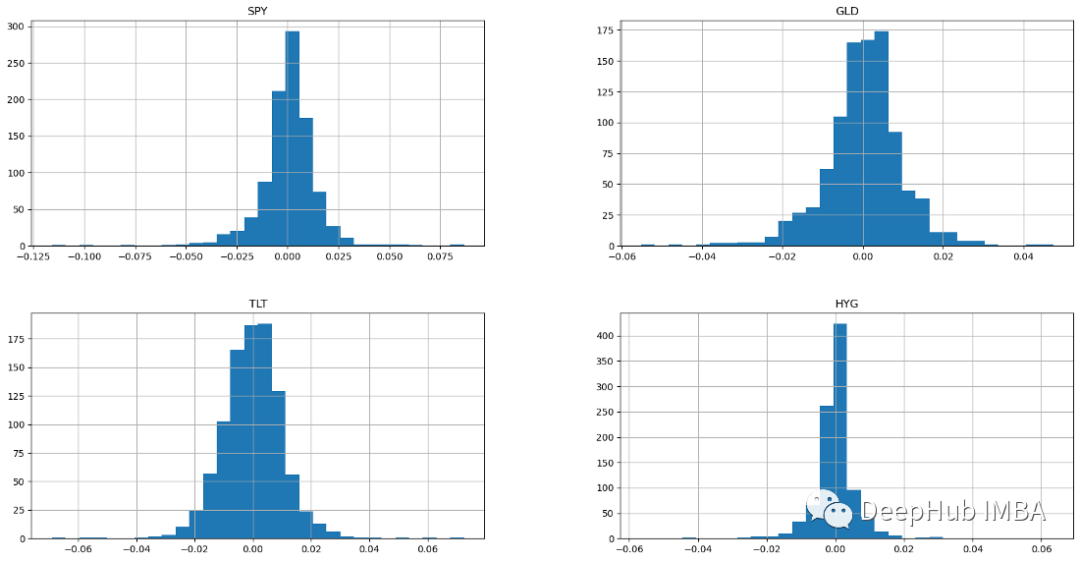
Keempat-empat kelas aset menunjukkan histogram taburan normal. Sampel dengan taburan normal mempunyai min aritmetik dan taburan yang sama di atas dan di bawah min (taburan normal yang juga dikenali sebagai taburan Gaussian adalah simetri). Jika pulangan diagihkan secara normal, lebih daripada 99% pulangan dijangka jatuh dalam tiga sisihan piawai min. Ciri-ciri taburan normal berbentuk loceng ini membolehkan penganalisis dan pelabur membuat inferens statistik yang lebih baik tentang jangkaan pulangan dan risiko saham. Saham dengan keluk loceng lazimnya adalah saham mewah dengan turun naik yang rendah dan boleh diramal.
Kadar anjakan maksima PENARIKAN
PENARISAN merujuk kepada nilai yang jatuh kepada relatif rendah. Ini adalah faktor risiko penting untuk dipertimbangkan oleh pelabur. Mari kita lukis perwakilan visual strategi menurun.
ffn.to_drawdown_series(data).plot(figsize=(15,10))
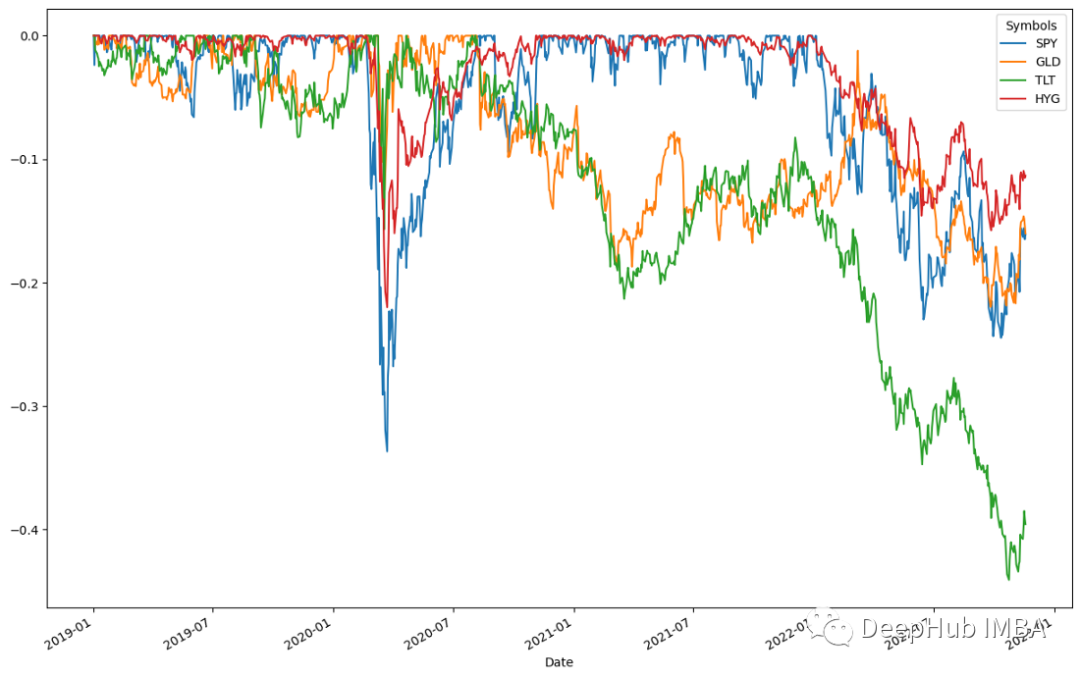
Keempat-empat aset merosot pada separuh pertama 2020, dengan SPY merekodkan penurunan terbesar sebanyak 0.5%. Kemudian, pada separuh pertama 2020, semua aset pulih serta-merta. Ini menunjukkan kadar pemulihan aset yang tinggi. Aset ini memuncak sekitar Julai 2020. Berikutan arah aliran ini, semua kelas aset menyaksikan penurunan yang sederhana sebaik sahaja pemulihan memuncak. Menurut keputusan, TLT akan mengalami penurunan terbesar sebanyak 0.5% pada separuh kedua 2022 sebelum pulih menjelang awal 2023.
MARKOWITZ Pengoptimuman min-varian
Pada tahun 1952, Markowitz mencadangkan teori portfolio min-varian, juga dikenali sebagai teori portfolio moden. Pelabur boleh menggunakan konsep ini untuk membina portfolio yang memaksimumkan pulangan yang dijangkakan berdasarkan tahap risiko tertentu. Berdasarkan kaedah Markowitz, kita boleh menjana "portfolio optimum".
returns.calc_mean_var_weights().as_format('.2%')
#结果
SPY 46.60%
GLD 53.40%
TLT 0.00%
HYG 0.00%
dtype: objectStatistik Korelasi
Korelasi ialah kaedah statistik yang digunakan untuk mengukur hubungan antara sekuriti. Maklumat ini terbaik dilihat menggunakan peta haba. Peta haba membolehkan kita melihat korelasi antara sekuriti.
returns.plot_corr_heatmap()
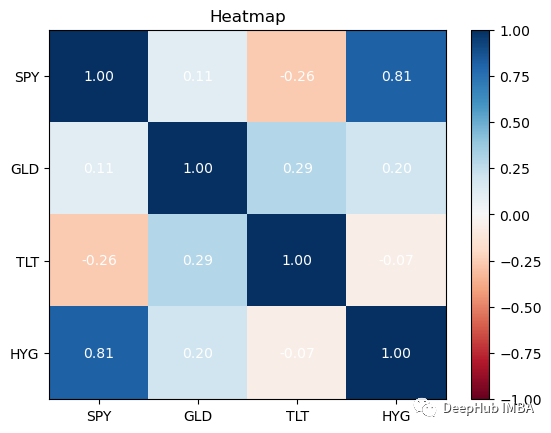
最好在你的投资组合中拥有相关性较低的资产。除了SPY与HYG,这四个资产类别的相关性都很低,这对我们的投资组合是不利的:因为如果拥有高度相关的不同资产组,即使你将风险分散在它们之间,从投资组合构建的角度来看,收益也会很少。
总结
通过分析和绘制的所有数据进行资产配置,可以建立一个投资组合,极大地改变基础投资的风险特征。还有很多我没有提到的,但可以帮助我们确定交易策略价值的起点。我们将在后续文章中添加更多的技术性能指标。
Atas ialah kandungan terperinci Strategi perdagangan dan analisis portfolio menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

