Menetapkan ambang terbaik untuk model pembelajaran mesin: Adakah 0.5 ambang terbaik untuk klasifikasi binari?

Untuk pengelasan binari, pengelas mengeluarkan skor nilai sebenar, dan kemudian ambang nilai untuk menghasilkan tindak balas binari. Sebagai contoh, regresi logistik mengeluarkan kebarangkalian (nilai antara 0.0 dan 1.0 dengan markah yang sama atau melebihi 0.5 menghasilkan output positif (banyak model lain menggunakan ambang 0.5 secara lalai).

Tetapi menggunakan ambang lalai 0.5 adalah tidak sesuai. Dalam artikel ini saya akan menunjukkan cara memilih ambang terbaik daripada pengelas binari. Artikel ini akan menggunakan Plomber untuk melaksanakan eksperimen kami secara selari dan menggunakan penilaian-sklearn untuk menjana graf.

Di sini kami mengambil latihan regresi logistik sebagai contoh. Katakan kita sedang membangunkan sistem penyederhanaan kandungan, di mana model membenderakan siaran yang mengandungi kandungan berbahaya (imej, video, dsb.); kemudian seseorang melihatnya dan memutuskan sama ada kandungan itu perlu dialih keluar.

Bina pengelas binari mudah

Coretan kod berikut melatih pengelas kami:

import matplotlib.pyplot as plt
 import matplotlib as mpl
 from sklearn import datasets
 from sklearn.linear_model import LogisticRegression
 from sklearn.model_selection import train_test_split
 from sklearn_evaluation.plot import ConfusionMatrix
 
 # matplotlib settings
 mpl.rcParams['figure.figsize'] = (4, 4)
 mpl.rcParams['figure.dpi'] = 150
 
 # create sample dataset
 X, y = datasets.make_classification(1000, 10, n_informative=5, class_sep=0.4)
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
 
 # fit model
 clf = LogisticRegression()
 _ = clf.fit(X_train, y_train)

Sekarang mari kita membuat ramalan pada set ujian dan menilainya melalui Prestasi matriks kekeliruan:

# predict on the test set
 y_pred = clf.predict(X_test)
 
 # plot confusion matrix
 cm_dot_five = ConfusionMatrix(y_test, y_pred)
 cm_dot_five

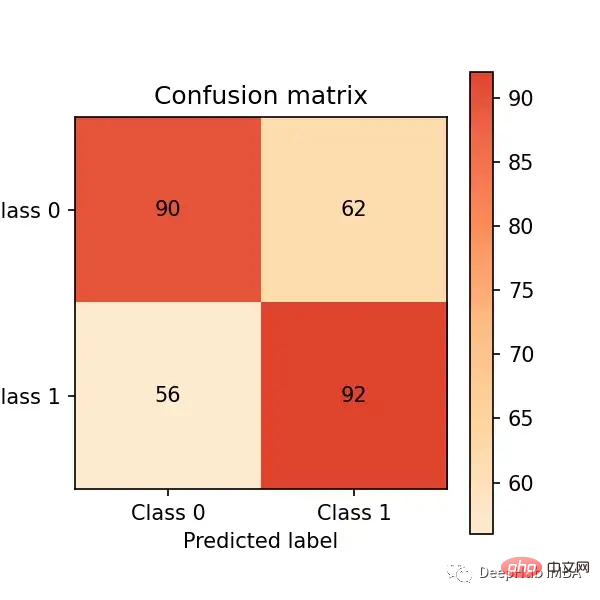
Matriks kekeliruan meringkaskan prestasi model dalam empat bidang:

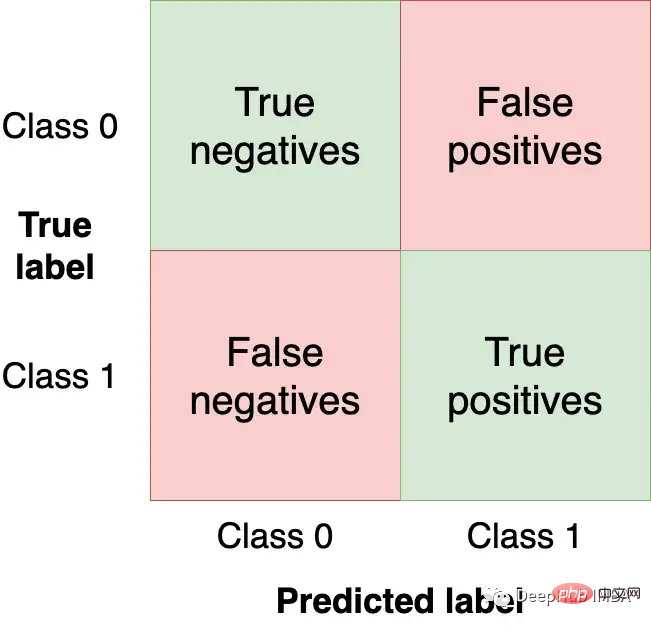
Kami ingin mendapatkan Dapatkan sebagai banyak pemerhatian (dari set ujian) di kuadran kanan bawah kerana ini adalah pemerhatian yang betul untuk model kami dapatkan. Kuadran lain adalah ralat model.

Menukar ambang model akan menukar nilai dalam matriks kekeliruan. Dalam contoh sebelumnya, menggunakan clf.predict, respons binari telah dikembalikan (iaitu menggunakan 0.5 sebagai ambang); tetapi kita boleh menggunakan fungsi clf.predict_proba untuk mendapatkan kebarangkalian mentah dan menggunakan ambang tersuai:

y_score = clf.predict_proba(X_test)

Kami boleh Menjadikan pengelas kami lebih agresif dengan menetapkan ambang yang lebih rendah (iaitu menandai lebih banyak siaran sebagai berbahaya) dan mencipta matriks kekeliruan baharu:

cm_dot_four = ConfusionMatrix(y_score[:, 1] >= 0.4, y_pred)

Pustaka penilaian sklearn memudahkan ini Membandingkan dua matriks:

cm_dot_five + cm_dot_four

Bahagian atas segitiga datang dari ambang 0.5 dan bahagian bawah datang dari ambang 0.4:

• Kedua-dua model meramalkan 0 untuk bilangan cerapan yang sama (ini kebetulan). 0.5 ambang: (90 + 56 = 146). 0.4 ambang: (78 + 68 = 146)
• Menurunkan ambang akan menghasilkan lebih banyak negatif palsu (dari 56 kepada 68)
• Menurunkan ambang akan meningkatkan positif sebenar (daripada 92 Contoh meningkat sebanyak 154 kes)

Perubahan ambang kecil sangat mempengaruhi matriks kekeliruan. Kami hanya menganalisis dua ambang. Kemudian jika kita boleh menganalisis prestasi model merentas semua nilai, kita boleh memahami dinamik ambang dengan lebih baik. Tetapi sebelum itu boleh berlaku, metrik baharu untuk penilaian model perlu ditakrifkan.

Setakat ini kami telah menilai model kami menggunakan nombor mutlak. Untuk memudahkan perbandingan dan penilaian, kami kini akan mentakrifkan dua metrik ternormal (nilainya antara 0.0 dan 1.0).

Ketepatan ialah perkadaran peristiwa yang diperhatikan yang dilabelkan (cth. siaran yang model kami anggap berbahaya, ia berbahaya). Ingat semula ialah perkadaran peristiwa sebenar yang diambil oleh model kami (iaitu, daripada semua siaran berbahaya, bahagian mana daripadanya dapat kami kesan).

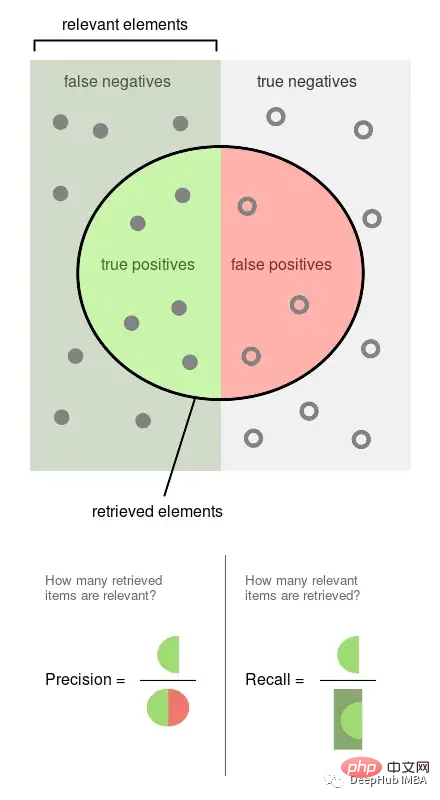
Gambar di atas adalah daripada Wikipedia, yang boleh menggambarkan dengan baik bagaimana kedua-dua penunjuk ini dikira Ketepatan dan ingatan kedua-duanya berkadar, jadi kedua-duanya adalah nisbah 0 daripada 1.

Jalankan percubaan

Kami akan mendapat ketepatan, ingat semula dan statistik lain berdasarkan beberapa ambang untuk lebih memahami cara ambang itu mempengaruhinya. Kami juga akan mengulangi percubaan ini beberapa kali untuk mengukur kebolehubahan.

Arahan dalam bahagian ini adalah semua arahan bash. Mereka perlu dilaksanakan dalam terminal Jika menggunakan Jupyter anda boleh menggunakan perintah ajaib %%sh.

Di sini kami menggunakan Plomber Cloud untuk menjalankan percubaan kami. Kerana ia membolehkan kami menjalankan eksperimen secara selari dan mendapatkan keputusan dengan cepat.

Mencipta buku nota yang sesuai dengan model dan mengira statistik untuk beberapa ambang, melaksanakan buku nota yang sama 20 kali secara selari.

curl -O https://raw.githubusercontent.com/ploomber/posts/master/threshold/fit.ipynb?utm_source=medium&utm_medium=blog&utm_campaign=threshold

Mari kita laksanakan buku nota ini (konfigurasi dalam fail akan memberitahu Plomber Cloud untuk menjalankannya 20 kali selari):

ploomber cloud nb fit.ipynb

Selepas beberapa minit, kita akan melihat 20 percubaan selesai :

ploomber cloud status @latest --summary
 
 status count
 -------- -------
 finished 20
 
 Pipeline finished. Check outputs:
 $ ploomber cloud products

Mari muat turun hasil percubaan yang disimpan dalam fail .csv:

ploomber cloud download 'threshold-selection/*.csv' --summary

Memvisualisasikan keputusan percubaan

akan memuatkan keputusan semua eksperimen dan memplotkannya sekali gus .

 from glob import glob
 
 import pandas as pd
 import numpy as np
 paths = glob('threshold-selection/**/*.csv')
 metrics = [pd.read_csv(path) for path in paths]
 
 for idx, df in enumerate(metrics):
plt.plot(df.threshold, df.precision, color='blue', alpha=0.2,
label='precision' if idx == 0 else None)
plt.plot(df.threshold, df.recall, color='green', alpha=0.2,
label='recall' if idx == 0 else None)
plt.plot(df.threshold, df.f1, color='orange', alpha=0.2,
label='f1' if idx == 0 else None)
 
 
 plt.grid()
 plt.legend()
 plt.xlabel('Threshold')
 plt.ylabel('Metric value')
 
 for handle in plt.legend().legendHandles:
handle.set_alpha(1)
 
 ax = plt.twinx()
 
 for idx, df in enumerate(metrics):
ax.plot(df.threshold, df.n_flagged,
label='flagged' if idx == 0 else None,
color='red', alpha=0.2)
 
 plt.ylabel('Flagged')
 ax.legend(loc=0)
 ax.legend().legendHandles[0].set_alpha(1)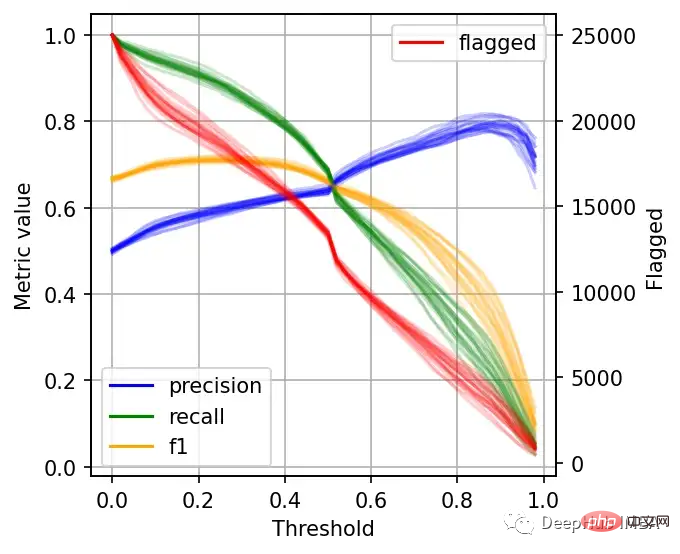

左边的刻度(从0到1)是我们的三个指标:精度、召回率和F1。F1分为精度与查全率的调和平均值，F1分的最佳值为1.0，最差值为0.0;F1对精度和召回率都是相同对待的，所以你可以看到它在两者之间保持平衡。如果你正在处理一个精确度和召回率都很重要的用例，那么最大化F1是一种可以帮助你优化分类器阈值的方法。

这里还包括一条红色曲线(右侧的比例)，显示我们的模型标记为有害内容的案例数量。

在这个的内容审核示例中，可能有X个的工作人员来人工审核模型标记的有害帖子，但是他们人数是有限的，因此考虑标记帖子的总数可以帮助我们更好地选择阈值:例如每天只能检查5000个帖子，那么模型找到10,000帖并不会带来任何的提高。如果我人工每天可以处理10000贴，但是模型只标记了100贴，那么显然也是浪费的。

当设置较低的阈值时，有较高的召回率(我们检索了大部分实际上有害的帖子)，但精度较低(包含了许多无害的帖子)。如果我们提高阈值，情况就会反转:召回率下降(错过了许多有害的帖子)，但精确度很高(大多数标记的帖子都是有害的)。

所以在为我们的二元分类器选择阈值时，我们必须在精度或召回率上妥协，因为没有一个分类器是完美的。我们来讨论一下如何推理选择合适的阈值。

选择最佳阈值

右边的数据会产生噪声(较大的阈值)。需要稍微清理一下，我们将重新创建这个图，我们将绘制2.5%、50%和97.5%的百分位数，而不是绘制所有值。

shape = (df.shape[0], len(metrics))
 precision = np.zeros(shape)
 recall = np.zeros(shape)
 f1 = np.zeros(shape)
 n_flagged = np.zeros(shape)
 for i, df in enumerate(metrics):
precision[:, i] = df.precision.values
recall[:, i] = df.recall.values
f1[:, i] = df.f1.values
n_flagged[:, i] = df.n_flagged.values
 precision_ = np.quantile(precision, q=0.5, axis=1)
 recall_ = np.quantile(recall, q=0.5, axis=1)
 f1_ = np.quantile(f1, q=0.5, axis=1)
 n_flagged_ = np.quantile(n_flagged, q=0.5, axis=1)
 plt.plot(df.threshold, precision_, color='blue', label='precision')
 plt.plot(df.threshold, recall_, color='green', label='recall')
 plt.plot(df.threshold, f1_, color='orange', label='f1')
 
 plt.fill_between(df.threshold, precision_interval[0],
precision_interval[1], color='blue',
alpha=0.2)
 
 plt.fill_between(df.threshold, recall_interval[0],
recall_interval[1], color='green',
alpha=0.2)
 
 
 plt.fill_between(df.threshold, f1_interval[0],
f1_interval[1], color='orange',
alpha=0.2)
 plt.xlabel('Threshold')
 plt.ylabel('Metric value')
 plt.legend()
 
 ax = plt.twinx()
 ax.plot(df.threshold, n_flagged_, color='red', label='flagged')
 ax.fill_between(df.threshold, n_flagged_interval[0],
n_flagged_interval[1], color='red',
alpha=0.2)
 
 ax.legend(loc=3)
 
 plt.ylabel('Flagged')
 plt.grid()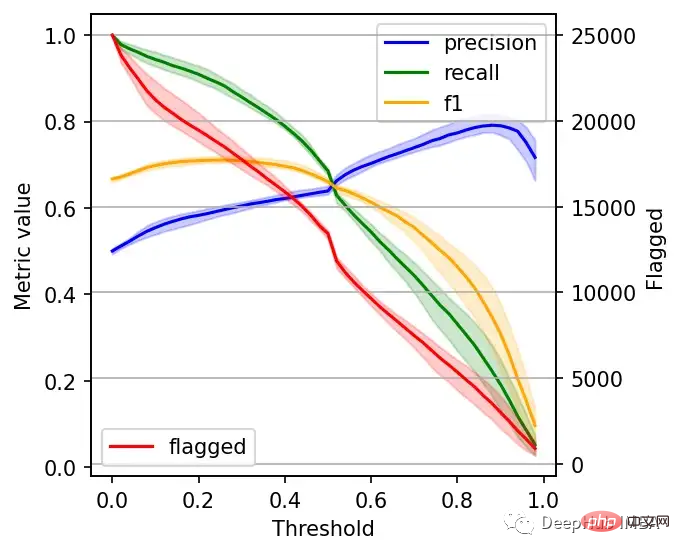

我们可以根据自己的需求选择阈值，例如检索尽可能多的有害帖子(高召回率)是否更重要?还是要有更高的确定性，我们标记的必须是有害的(高精度)?

如果两者都同等重要，那么在这些条件下优化的常用方法就是最大化F-1分数:

idx = np.argmax(f1_)
 prec_lower, prec_upper = precision_interval[0][idx], precision_interval[1][idx]
 rec_lower, rec_upper = recall_interval[0][idx], recall_interval[1][idx]
 threshold = df.threshold[idx]
 
 print(f'Max F1 score: {f1_[idx]:.2f}')
 print('Metrics when maximizing F1 score:')
 print(f' - Threshold: {threshold:.2f}')
 print(f' - Precision range: ({prec_lower:.2f}, {prec_upper:.2f})')
 print(f' - Recall range: ({rec_lower:.2f}, {rec_upper:.2f})')
 
 #结果
 Max F1 score: 0.71
 Metrics when maximizing F1 score:
- Threshold: 0.26
- Precision range: (0.58, 0.61)
- Recall range: (0.86, 0.90)

在很多情况下很难决定这个折中，所以加入一些约束条件会有一些帮助。

假设我们有10个人审查有害的帖子，他们可以一起检查5000个。那么让我们看看指标，如果我们修改了阈值，让它标记了大约5000个帖子:

idx = np.argmax(n_flagged_ <= 5000)
 
 prec_lower, prec_upper = precision_interval[0][idx], precision_interval[1][idx]
 rec_lower, rec_upper = recall_interval[0][idx], recall_interval[1][idx]
 threshold = df.threshold[idx]
 
 print('Metrics when limiting to a maximum of 5,000 flagged events:')
 print(f' - Threshold: {threshold:.2f}')
 print(f' - Precision range: ({prec_lower:.2f}, {prec_upper:.2f})')
 print(f' - Recall range: ({rec_lower:.2f}, {rec_upper:.2f})')
 
 # 结果
 Metrics when limiting to a maximum of 5,000 flagged events:
- Threshold: 0.82
- Precision range: (0.77, 0.81)
- Recall range: (0.25, 0.36)

如果需要进行汇报，我们可以在在展示结果时展示一些替代方案:比如在当前约束条件下(5000个帖子)的模型性能，以及如果我们增加团队(比如通过增加一倍的规模)，我们可以做得更好。

总结

二元分类器的最佳阈值是针对业务结果进行优化并考虑到流程限制的阈值。通过本文中描述的过程，你可以更好地为用例决定最佳阈值。

另外，Ploomber Cloud!提供一些免费的算力!如果你需要一些免费的服务可以试试它。

Atas ialah kandungan terperinci Menetapkan ambang terbaik untuk model pembelajaran mesin: Adakah 0.5 ambang terbaik untuk klasifikasi binari?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!