Bagaimana untuk melaksanakan keturunan kecerunan untuk menyelesaikan regresi logistik dalam python

Regression Linear

1. Fungsi regresi linear

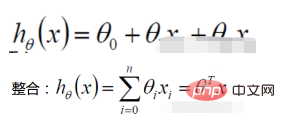
Definisi fungsi kemungkinan: nilai sampel bersama X Fungsi berikut

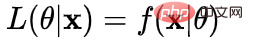
fungsi kemungkinan : Apakah jenis parameter sebenarnya nilai sebenar apabila digabungkan dengan data kami?

2. Fungsi kemungkinan regresi linear

Kemungkinan log:

3. Fungsi objektif regresi linear

(ungkapan ralat, tujuan kami adalah untuk membuat nilai sebenar sebelum nilai ramalan Ralat adalah yang terkecil)

(derivatif ialah 0 untuk mendapatkan nilai ekstrem, dan parameter fungsi diperoleh)

Regression logistik

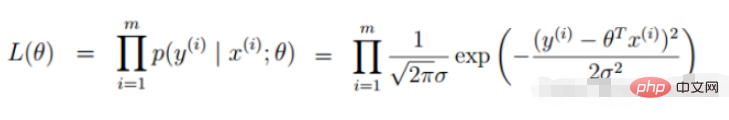
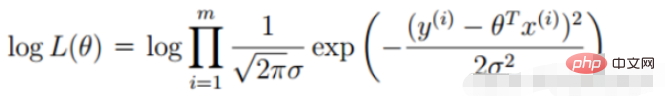
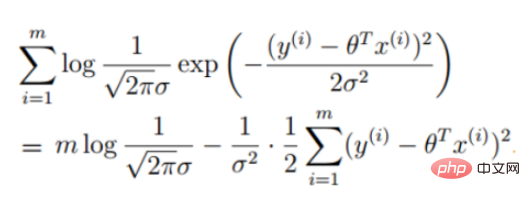
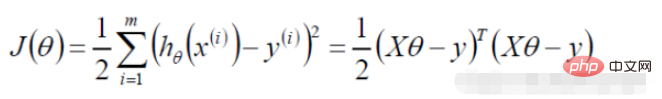
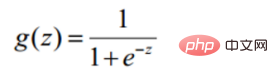
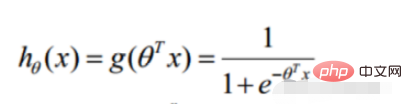
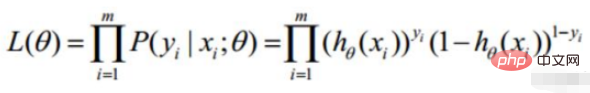
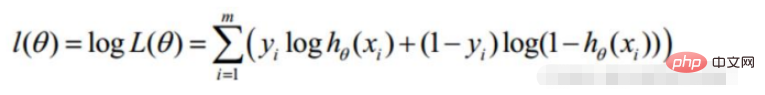
Regression logistik adalah dalam talian Hasilnya regresi linear ditambah lapisan fungsi Sigmoid

1. Fungsi regresi logistik

2. Fungsi kemungkinan regresi logistik

menganggap bahawa data mematuhi pengedaran Bernoulli

Kemungkinan log:

diperkenalkan

Diubah menjadi tugas penurunan kecerunan, fungsi objektif regresi logistik

Diselesaikan dengan kaedah keturunan kecerunan

Pemahaman saya adalah untuk mendapatkan dan mengemas kini parameter, berhenti selepas mencapai keadaan tertentu, dan mendapatkan anggaran optimum penyelesaian

Pelaksanaan kod

Fungsi sigmoid

def sigmoid(z):    
   return 1 / (1 + np.exp(-z))

Fungsi ramalan

def model(X, theta):    
    return sigmoid(np.dot(X, theta.T))

Fungsi objektif

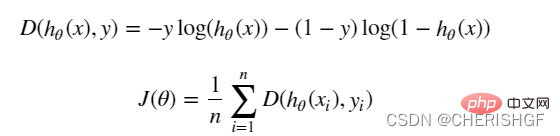
def cost(X, y, theta):    
     left = np.multiply(-y, np.log(model(X, theta)))    
     right = np.multiply(1 - y, np.log(1 - model(X, theta)))    
     return np.sum(left - right) / (len(X))

def gradient(X, y, theta):    
  grad = np.zeros(theta.shape)    
  error = (model(X, theta)- y).ravel()    
  for j in range(len(theta.ravel())): #for each parmeter        
     term = np.multiply(error, X[:,j])        
     grad[0, j] = np.sum(term) / len(X)    
   return grad

Kecerunan

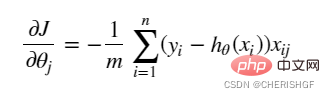
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
 
def stopCriterion(type, value, threshold):
    # 设定三种不同的停止策略
    if type == STOP_ITER:  # 设定迭代次数
        return value > threshold
    elif type == STOP_COST:  # 根据损失值停止
        return abs(value[-1] - value[-2]) < threshold
    elif type == STOP_GRAD:  # 根据梯度变化停止
        return np.linalg.norm(value) < threshold

Strategi berhenti keturunan kecerunan

import numpy.random
#洗牌
def shuffleData(data):
    np.random.shuffle(data)
    cols = data.shape[1]
    X = data[:, 0:cols-1]
    y = data[:, cols-1:]
    return X, y

Sampel rombakan

def descent(data, theta, batchSize, stopType, thresh, alpha):
    # 梯度下降求解
 
    init_time = time.time()
    i = 0  # 迭代次数
    k = 0  # batch
    X, y = shuffleData(data)
    grad = np.zeros(theta.shape)  # 计算的梯度
    costs = [cost(X, y, theta)]  # 损失值
 
    while True:
        grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
        k += batchSize  # 取batch数量个数据
        if k >= n:
            k = 0
            X, y = shuffleData(data)  # 重新洗牌
        theta = theta - alpha * grad  # 参数更新
        costs.append(cost(X, y, theta))  # 计算新的损失
        i += 1
 
        if stopType == STOP_ITER:
            value = i
        elif stopType == STOP_COST:
            value = costs
        elif stopType == STOP_GRAD:
            value = grad
        if stopCriterion(stopType, value, thresh): break
 
    return theta, i - 1, costs, grad, time.time() - init_time

Penyelesaian keturunan kecerunan

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import numpy.random
import time
 
 
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
 
def model(X, theta):
    return sigmoid(np.dot(X, theta.T))
 
 
def cost(X, y, theta):
    left = np.multiply(-y, np.log(model(X, theta)))
    right = np.multiply(1 - y, np.log(1 - model(X, theta)))
    return np.sum(left - right) / (len(X))
 
 
def gradient(X, y, theta):
    grad = np.zeros(theta.shape)
    error = (model(X, theta) - y).ravel()
    for j in range(len(theta.ravel())):  # for each parmeter
        term = np.multiply(error, X[:, j])
        grad[0, j] = np.sum(term) / len(X)
    return grad
 
 
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
 
 
def stopCriterion(type, value, threshold):
    # 设定三种不同的停止策略
    if type == STOP_ITER:  # 设定迭代次数
        return value > threshold
    elif type == STOP_COST:  # 根据损失值停止
        return abs(value[-1] - value[-2]) < threshold
    elif type == STOP_GRAD:  # 根据梯度变化停止
        return np.linalg.norm(value) < threshold
 
 
# 洗牌
def shuffleData(data):
    np.random.shuffle(data)
    cols = data.shape[1]
    X = data[:, 0:cols - 1]
    y = data[:, cols - 1:]
    return X, y
 
 
def descent(data, theta, batchSize, stopType, thresh, alpha):
    # 梯度下降求解
 
    init_time = time.time()
    i = 0  # 迭代次数
    k = 0  # batch
    X, y = shuffleData(data)
    grad = np.zeros(theta.shape)  # 计算的梯度
    costs = [cost(X, y, theta)]  # 损失值
 
    while True:
        grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
        k += batchSize  # 取batch数量个数据
        if k >= n:
            k = 0
            X, y = shuffleData(data)  # 重新洗牌
        theta = theta - alpha * grad  # 参数更新
        costs.append(cost(X, y, theta))  # 计算新的损失
        i += 1
 
        if stopType == STOP_ITER:
            value = i
        elif stopType == STOP_COST:
            value = costs
        elif stopType == STOP_GRAD:
            value = grad
        if stopCriterion(stopType, value, thresh): break
 
    return theta, i - 1, costs, grad, time.time() - init_time
 
 
def runExpe(data, theta, batchSize, stopType, thresh, alpha):
    # import pdb
    # pdb.set_trace()
    theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)
    name = "Original" if (data[:, 1] > 2).sum() > 1 else "Scaled"
    name += " data - learning rate: {} - ".format(alpha)
    if batchSize == n:
        strDescType = "Gradient"  # 批量梯度下降
    elif batchSize == 1:
        strDescType = "Stochastic"  # 随机梯度下降
    else:
        strDescType = "Mini-batch ({})".format(batchSize)  # 小批量梯度下降
    name += strDescType + " descent - Stop: "
    if stopType == STOP_ITER:
        strStop = "{} iterations".format(thresh)
    elif stopType == STOP_COST:
        strStop = "costs change < {}".format(thresh)
    else:
        strStop = "gradient norm < {}".format(thresh)
    name += strStop
    print("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(
        name, theta, iter, costs[-1], dur))
    fig, ax = plt.subplots(figsize=(12, 4))
    ax.plot(np.arange(len(costs)), costs, 'r')
    ax.set_xlabel('Iterations')
    ax.set_ylabel('Cost')
    ax.set_title(name.upper() + ' - Error vs. Iteration')
    return theta
 
 
path = 'data' + os.sep + 'LogiReg_data.txt'
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
positive = pdData[pdData['Admitted'] == 1]
negative = pdData[pdData['Admitted'] == 0]
 
# 画图观察样本情况
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
 
pdData.insert(0, 'Ones', 1)
 
# 划分训练数据与标签
orig_data = pdData.values
cols = orig_data.shape[1]
X = orig_data[:, 0:cols - 1]
y = orig_data[:, cols - 1:cols]
# 设置初始参数0
theta = np.zeros([1, 3])
 
# 选择的梯度下降方法是基于所有样本的
n = 100
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)
runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)
runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)
runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)
runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)
runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)
 
from sklearn import preprocessing as pp
 
# 数据预处理
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
 
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)
runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001)
theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002 / 5, alpha=0.001)
runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002 * 2, alpha=0.001)
 
 
# 设定阈值
def predict(X, theta):
    return [1 if x >= 0.5 else 0 for x in model(X, theta)]
 
 
# 计算精度
scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))

Contoh rombakan

rrreee

Penyelesaian keturunan kecerunan

rrreeerrreeeKebaikan dan keburukan regresi logistik

• Kelebihan

• Borangnya mudah dan kebolehtafsiran model sangat baik. Daripada berat ciri, kita boleh melihat kesan ciri yang berbeza pada hasil akhir Jika nilai berat ciri tertentu agak tinggi, maka ciri ini akan memberi kesan yang lebih besar pada hasil akhir.

• Model berfungsi dengan baik. Ia boleh diterima dalam kejuruteraan (sebagai garis asas jika kejuruteraan ciri dilakukan dengan baik, kesannya tidak akan terlalu buruk, dan kejuruteraan ciri boleh dibangunkan secara selari, sangat mempercepatkan pembangunan.

• Kelajuan latihan lebih pantas. Apabila mengklasifikasikan, jumlah pengiraan hanya berkaitan dengan bilangan ciri. Selain itu, sgd pengoptimuman yang diedarkan bagi regresi logistik adalah agak matang, dan kelajuan latihan boleh dipertingkatkan lagi melalui mesin timbunan, supaya kami boleh mengulang beberapa versi model dalam tempoh yang singkat.

• Ia mengambil sedikit sumber, terutamanya ingatan. Kerana hanya nilai ciri setiap dimensi perlu disimpan.

Selesaikan hasil output dengan mudah. Regresi logistik dengan mudah boleh mendapatkan hasil klasifikasi akhir, kerana output ialah skor kebarangkalian setiap sampel, dan kita boleh memotong skor kebarangkalian ini dengan mudah, iaitu, membahagikan ambang (yang lebih besar daripada ambang tertentu diklasifikasikan ke dalam satu kategori, dan yang kurang daripada ambang tertentu dikelaskan kepada satu kategori).

• Kelemahan
  Ketepatannya tidak begitu tinggi. Oleh kerana bentuknya sangat mudah (sangat serupa dengan model linear), adalah sukar untuk menyesuaikan pengedaran data sebenar.

• Sukar untuk menangani masalah ketidakseimbangan data. Sebagai contoh: Jika kita menghadapi masalah di mana sampel positif dan negatif adalah sangat tidak seimbang, seperti nisbah sampel positif dan negatif ialah 10000:1 Jika kita meramalkan semua sampel sebagai positif, kita juga boleh membuat nilai fungsi kehilangan lebih kecil. Tetapi sebagai pengelas, keupayaannya untuk membezakan sampel positif dan negatif tidak akan menjadi sangat baik.

• Memproses data tak linear lebih menyusahkan. Regresi logistik, tanpa memperkenalkan kaedah lain, hanya boleh mengendalikan data boleh dipisahkan secara linear, atau selanjutnya, mengendalikan masalah klasifikasi binari.

• Regression logistik itu sendiri tidak boleh menapis ciri. Kadangkala, kami menggunakan gbdt untuk menapis ciri dan kemudian menggunakan regresi logistik.

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan keturunan kecerunan untuk menyelesaikan regresi logistik dalam python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!