Rumah >Java >javaTutorial >Bagaimana untuk melaksanakan algoritma Kruskal di Jawa
Bagaimana untuk melaksanakan algoritma Kruskal di Jawa
- 王林ke hadapan
- 2023-05-11 22:19:04908semak imbas
Pengenalan
Terdapat satu lagi algoritma untuk membina pokok rentang minimum, algoritma Kruskal: Biarkan graf G = (V, E) ialah graf wajaran bersambung tidak berarah, V = {1, 2,. .. n}; Katakan pokok rentang minimum T = (V, TE Keadaan awal pokok itu hanya mempunyai n nod dan graf tidak bersambung tanpa tepi T = (V, {}). n nod sebagai n dahan bersambung terpencil. Ia mula-mula mengisih semua tepi mengikut beratnya dari kecil ke besar, dan kemudian jika bilangan tepi untuk dipilih dalam T kurang daripada n-1, ia membuat pemilihan tamak seperti ini: pilih tepi (i, j) dengan berat terkecil dalam set tepi E ), jika menambah tepi (i, j) pada set TE tidak menghasilkan kitaran, maka tambah tepi (i, j) pada set tepi TE, iaitu, gunakan tepi (i , j) untuk menggabungkan dua cawangan ke dalam cawangan yang disambungkan ; Padamkan tepi (i, j) daripada set E dan teruskan pemilihan tamak di atas sehingga semua nod dalam T berada pada cawangan bersambung yang sama. Pada masa ini, tepi n-1 yang dipilih betul-betul membentuk pokok rentang minimum T graf G.
Algoritma Kruskal menggunakan kaedah yang sangat pintar, iaitu menggunakan set untuk mengelakkan bulatan jika titik permulaan dan titik akhir tepi yang dipilih adalah kedua-duanya dalam set T, boleh disimpulkan bahawa gelung; akan terbentuk, dan kedua-dua nod yang ditukar tidak boleh dimiliki oleh koleksi yang sama.
Langkah algoritma
1 Permulaan. Isih semua tepi dalam tertib menaik berat, dan mulakan setiap nombor set nod kepada nombornya sendiri.
2 Pilih tepi (u, v) dengan berat terkecil dalam susunan yang disusun.
3 Jika nod u dan v tergolong dalam dua cabang bersambung yang berbeza, tambahkan tepi (u, v) pada set tepi TE dan cantumkan dua cabang yang bersambung.
4 Jika bilangan tepi yang dipilih kurang daripada n-1, pergi ke langkah 2, jika tidak, algoritma akan tamat.
1. Gambar rajah yang dibina
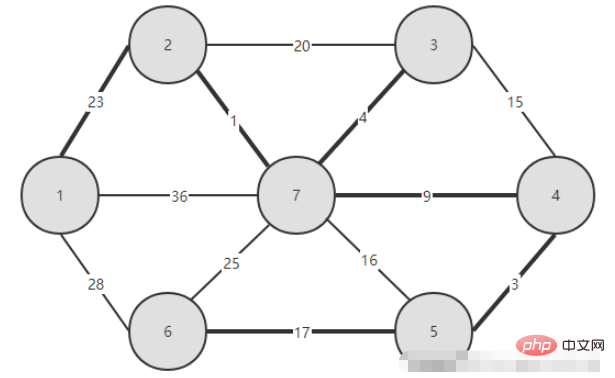
2. Kod
package graph.kruskal;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
public class Kruskal {
static final int N = 100;
static int fa[] = new int[N];
static int n;
static int m;
static Edge e[] = new Edge[N * N];
static List<Edge> edgeList = new ArrayList();
static {
for (int i = 0; i < e.length; i++) {
e[i] = new Edge();
}
}
// 初始化集合号为自身
static void Init(int n) {
for (int i = 1; i <= n; i++)
fa[i] = i;
}
// 合并
static int Merge(int a, int b) {
int p = fa[a];
int q = fa[b];
if (p == q) return 0;
for (int i = 1; i <= n; i++) { // 检查所有结点,把集合号是 q 的改为 p
if (fa[i] == q)
fa[i] = p; // a 的集合号赋值给 b 集合号
}
return 1;
}
// 求最小生成树
static int Kruskal(int n) {
int ans = 0;
Collections.sort(edgeList);
for (int i = 0; i < m; i++)
if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
ans += edgeList.get(i).w;
n--;
if (n == 1)//n-1次合并算法结束
return ans;
}
return 0;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
Init(n);
for (int i = 1; i <= m; i++) {
e[i].u = scanner.nextInt();
e[i].v = scanner.nextInt();
e[i].w = scanner.nextInt();
edgeList.add(e[i]);
}
System.out.println("最小的花费是:" + Kruskal(n));
}
}
class Edge implements Comparable {
int u;
int w;
int v;
@Override
public int compareTo(Object o) {
if (this.w > ((Edge) o).w) {
return 1;
} else if (this.w == ((Edge) o).w) {
return 0;
} else {
return -1;
}
}
}3. Putih adalah output.
Atas ialah kandungan terperinci Bagaimana untuk melaksanakan algoritma Kruskal di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

