Jangan mengejar model besar secara membabi buta dan mengumpul kuasa pengkomputeran! Shen Xiangyang, Cao Ying dan Ma Yi mencadangkan dua prinsip asas untuk memahami AI: parsimoni dan konsistensi diri

Dalam dua tahun kebelakangan ini, model besar yang "berusaha hebat (kuasa pengkomputeran) boleh menghasilkan keajaiban" telah menjadi trend yang diikuti oleh kebanyakan penyelidik dalam bidang kecerdasan buatan. Walau bagaimanapun, masalah kos pengiraan dan penggunaan sumber yang besar di belakangnya telah beransur-ansur menjadi jelas Sesetengah saintis telah mula melihat dengan serius pada model besar dan secara aktif mencari penyelesaian. Penyelidikan baharu menunjukkan bahawa mencapai prestasi cemerlang model AI tidak semestinya bergantung pada kuasa pengkomputeran timbunan dan saiz timbunan.

Pembelajaran mendalam telah berkembang pesat selama sepuluh tahun Harus dikatakan bahawa peluang dan kesesakan telah menarik perhatian dan perbincangan selama sepuluh tahun penyelidikan dan amalan ini.

Antaranya, dimensi kesesakan, yang paling menarik perhatian ialah ciri kotak hitam pembelajaran mendalam (kekurangan tafsiran) dan "hasil ajaib dengan usaha yang hebat" (parameter model adalah semakin besar dan lebih besar, Permintaan untuk kuasa pengkomputeran semakin besar dan semakin besar, dan kos pengkomputeran semakin tinggi dan lebih tinggi). Selain itu, terdapat juga isu seperti kestabilan model yang tidak mencukupi dan kelemahan keselamatan.

Pada asasnya, masalah ini sebahagiannya disebabkan oleh sifat sistem "gelung terbuka" rangkaian saraf dalam. Untuk memecahkan "kutukan" bahagian B dalam pembelajaran mendalam, mungkin tidak cukup dengan hanya mengembangkan skala model dan kuasa pengkomputeran Sebaliknya, kita perlu mengesan sumber, dari prinsip asas sistem kecerdasan buatan, dan dari perspektif baharu (seperti gelung tertutup) Fahami "kepintaran".

Pada 12 Julai, tiga saintis China terkenal dalam bidang kecerdasan buatan, Ma Yi, Cao Ying dan Shun Xiangyang, bersama-sama menerbitkan artikel mengenai arXiv, "On the Principles of Parsimony and Self-Consistency for the Emergence of Intelligence", yang mencadangkan rangka kerja baharu untuk memahami rangkaian dalam: transkripsi gelung tertutup mampatan.

Rangka kerja ini mengandungi dua prinsip: parsimoni dan ketekalan diri, yang masing-masing sepadan dengan "apa yang perlu dipelajari" dalam proses pembelajaran model AI dan "cara belajar" dipertimbangkan menjadi dua asas kecerdasan buatan/semula jadi, dan telah menarik perhatian meluas dalam bidang penyelidikan kecerdasan buatan di dalam dan luar negara.

Pautan kertas:

https://arxiv.org/pdf/2207.04630.pdf

Tiga saintis percaya bahawa kecerdasan sebenar mesti mempunyai dua ciri, satu kebolehjelasan dan satu lagi kebolehhitungan.

Walau bagaimanapun, sepanjang dekad yang lalu, kemajuan dalam kecerdasan buatan adalah berdasarkan kaedah pembelajaran mendalam yang menggunakan latihan "brute force" model, dalam hal ini walaupun model AI juga boleh memperoleh kefungsian Modul digunakan untuk persepsi dan membuat keputusan, tetapi perwakilan ciri yang dipelajari selalunya tersirat dan sukar untuk ditafsir.

Selain itu, bergantung semata-mata pada timbunan kuasa pengkomputeran untuk melatih model juga menyebabkan skala model AI terus meningkat, kos pengkomputeran terus meningkat, dan banyak masalah telah timbul dalam aplikasi pendaratan, seperti Neural Collapse membawa kepada kekurangan kepelbagaian dalam perwakilan yang dipelajari, keruntuhan corak membawa kepada kekurangan kestabilan dalam latihan, model mempunyai kepekaan yang lemah terhadap kebolehsuaian dan melupakan bencana, dan sebagainya.

Tiga saintis percaya bahawa masalah di atas berlaku kerana dalam rangkaian dalam semasa, latihan model diskriminatif untuk klasifikasi dan model generatif untuk pensampelan atau main semula Kebanyakannya berasingan. Model sedemikian biasanya sistem gelung terbuka yang memerlukan latihan hujung ke hujung melalui penyeliaan atau penyeliaan diri. Wiener dan lain-lain telah lama mendapati bahawa sistem gelung terbuka sedemikian tidak dapat membetulkan ralat dalam ramalan secara automatik, dan juga tidak dapat menyesuaikan diri dengan perubahan dalam persekitaran.

Oleh itu, mereka menganjurkan untuk memperkenalkan "maklum balas gelung tertutup" ke dalam sistem kawalan supaya sistem boleh belajar membetulkan ralat sendiri. Dalam kajian ini, mereka juga mendapati bahawa dengan menggunakan model diskriminatif dan model generatif untuk membentuk sistem gelung tertutup yang lengkap, sistem boleh belajar secara bebas (tanpa penyeliaan luar), dan lebih cekap, stabil dan boleh disesuaikan.

Nota gambar: Dari kiri ke kanan ialah Shun Xiangyang (Kerusi Presiden Profesor Hong Kong, China dan Shenzhen, ahli akademik asing Akademi Kejuruteraan Kebangsaan, bekas naib presiden eksekutif global Microsoft), Cao Ying (Akademik Akademi Sains Kebangsaan, Profesor di University of California, Berkeley) dan Ma Yi (Profesor di University of California, Berkeley).

Dua prinsip kecerdasan: parsimoni dan konsistensi diri

Dalam karya ini, tiga saintis mencadangkan penjelasan Dua prinsip asas kecerdasan buatan adalah parsimoni dan konsistensi diri (juga dikenali sebagai "konsistensi diri").

Kesederhanaan

Apa yang dipanggil kesederhanaan ialah "apa yang perlu dipelajari". Prinsip parsimoni pintar memerlukan sistem untuk mendapatkan perwakilan yang padat dan berstruktur dengan cara yang cekap dari segi pengiraan. Iaitu, sistem pintar boleh menggunakan mana-mana model berstruktur yang menerangkan dunia, selagi mereka boleh mensimulasikan struktur berguna secara ringkas dan cekap dalam data deria kehidupan sebenar. Sistem harus dapat menilai kualiti model pembelajaran dengan tepat dan cekap menggunakan metrik yang asas, universal, mudah dikira dan dioptimumkan.

Mengambil pemodelan data visual sebagai contoh, prinsip parsimoni cuba mencari transformasi (tidak linear) f untuk mencapai matlamat berikut:

Mampatan: deria berdimensi tinggi data x Petakan kepada perwakilan berdimensi rendah z;

Linearisasi: memetakan setiap jenis objek yang diedarkan pada sub-manifold bukan linear kepada subruang linear: menukarkan kelas yang berbeza kepada subruang dengan asas bebas atau tidak koheren maksimum.

Iaitu, data dunia sebenar yang mungkin terletak pada satu siri submanifold dimensi rendah dalam ruang dimensi tinggi ditukarkan kepada siri subruang linear dimensi rendah bebas. Model ini dipanggil "perwakilan diskriminatif linear" (LDR) Proses pemampatan ditunjukkan dalam Rajah 2:

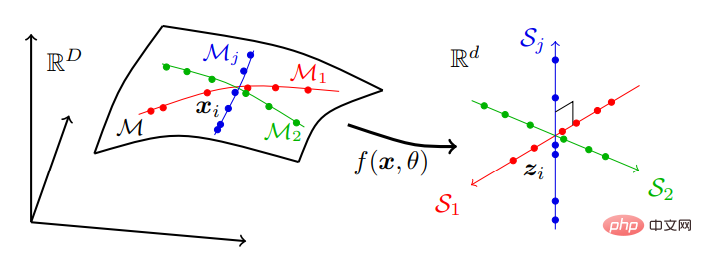Rajah 2: Mencari perwakilan diskriminatif jumlah linear, Pemetaan dimensi tinggi data deria, biasanya diedarkan pada banyak submanifold berdimensi rendah bukan linear, kepada set subruang linear bebas dengan dimensi yang sama dengan submanifold.

Dalam keluarga model LDR, terdapat ukuran intrinsik parsimoni. Iaitu, memandangkan LDR, kita boleh mengira jumlah "isipadu" yang direntangi oleh semua ciri ke atas semua subruang dan jumlah "isipadu" yang dibentangkan oleh ciri setiap kategori. Nisbah antara dua jilid ini kemudiannya memberikan ukuran semula jadi tentang betapa baiknya model LDR (lebih besar selalunya lebih baik).

Menurut teori maklumat, volum taburan boleh diukur dengan herotan kadarnya.

Karya oleh pasukan Ma Yi pada 2022 "ReduNet: Rangkaian Dalam Kotak Putih daripada Prinsip Memaksimumkan Pengurangan Kadar" menunjukkan bahawa jika anda menggunakan fungsi herotan kadar Gaussian dan memilih Rangkaian dalam tujuan umum (seperti ResNet) memodelkan pemetaan f(x, θ) dengan meminimumkan kadar pengekodan.

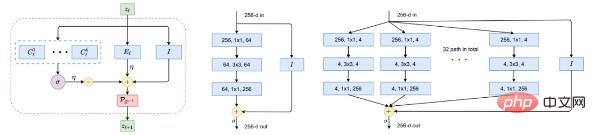Rajah 5: Blok binaan pemetaan tak linear f. Kiri: Lapisan ReduNet, sebagai lelaran pendakian kecerunan yang diunjurkan, yang terdiri daripada operator linear yang mengembang atau memampatkan, softmax tak linear, sambungan langkau dan normalisasi. Tengah dan kanan gambar: satu lapisan ResNet dan ResNeXt masing-masing.

Pembaca yang cerdik mungkin telah menyedari bahawa gambarajah sebegitu sangat serupa dengan rangkaian dalam yang popular "dicuba dan diuji" seperti ResNet (Rajah 5 tengah), termasuk lajur selari dalam ResNeXt (Rajah 5 kanan) dan Campuran Pakar (KPM).

Dari perspektif skema pengoptimuman yang terungkap, ini memberikan penjelasan yang kuat untuk kelas rangkaian saraf dalam. Malah sebelum kebangkitan rangkaian dalam moden, skim pengoptimuman berulang untuk mencari kesederhanaan seperti ISTA atau FISTA telah ditafsirkan sebagai rangkaian dalam yang boleh dipelajari.

Melalui eksperimen, mereka menunjukkan bahawa pemampatan boleh melahirkan cara yang membina untuk memperoleh rangkaian saraf dalam, termasuk seni bina dan parameternya, sebagai kotak putih yang boleh ditafsir sepenuhnya: Lapisannya melakukan berulang dan pengoptimuman tambahan ke arah matlamat berprinsip untuk menggalakkan kesederhanaan. Oleh itu, untuk rangkaian dalam yang diperolehi itu, ReduNets, bermula dari data X sebagai input, operator dan parameter setiap lapisan dibina dan dimulakan dengan cara terbentang ke hadapan sepenuhnya.

Ini sangat berbeza daripada amalan popular dalam pembelajaran mendalam: bermula dengan rangkaian yang dibina dan dimulakan secara rawak dan kemudian membuat pelarasan global melalui perambatan belakang. Secara amnya dipercayai bahawa otak tidak mungkin menggunakan perambatan balik sebagai mekanisme pembelajarannya kerana keperluan untuk sinaps simetri dan bentuk maklum balas yang kompleks. Di sini, pengoptimuman buka gulungan ke hadapan hanya bergantung pada operasi antara lapisan bersebelahan yang boleh dirangkai dan oleh itu lebih mudah untuk dilaksanakan dan dieksploitasi.

"Evolusi" rangkaian saraf tiruan sepanjang dekad yang lalu mudah difahami dan amat membantu apabila kita menyedari bahawa peranan rangkaian dalam itu sendiri adalah untuk melaksanakan pengoptimuman berulang (berasaskan kecerunan) untuk memampatkan, menlinearkan dan mengecilkan data. Yu menerangkan sebab hanya beberapa sistem AI yang menonjol melalui proses pemilihan manusia: daripada MLP ke CNN ke ResNet ke Transformer.

Sebaliknya, carian rawak untuk struktur rangkaian, seperti carian seni bina saraf, tidak menghasilkan seni bina rangkaian yang boleh melaksanakan tugas umum dengan berkesan. Mereka membuat hipotesis bahawa seni bina yang berjaya menjadi semakin berkesan dan fleksibel dalam mensimulasikan skim pengoptimuman berulang untuk pemampatan data. Ini boleh dicontohkan oleh persamaan yang dinyatakan sebelum ini antara ReduNet dan ResNet/ResNeXt. Sudah tentu, terdapat banyak contoh lain.

Ketekalan kendiri

Ketekalan diri adalah mengenai "cara belajar", iaitu sistem pintar autonomi belajar dengan meminimumkan yang diperhatikan dan pengeluar semula untuk mencari model yang paling konsisten diri untuk memerhati dunia luar.

Prinsip parsimoni sahaja tidak memastikan model pembelajaran dapat menangkap semua maklumat penting dalam data dunia luaran persepsi.

Sebagai contoh, memetakan setiap kelas kepada vektor "satu-panas" satu dimensi dengan meminimumkan entropi silang boleh dilihat sebagai bentuk parsimoni. Ia mungkin mempelajari pengelas yang baik, tetapi ciri yang dipelajari runtuh menjadi tunggal, yang dikenali sebagai "runtuh saraf." Ciri yang dipelajari tidak mengandungi maklumat yang mencukupi untuk menjana semula data asal. Walaupun kita menganggap kelas model LDR yang lebih umum, objektif pengurangan kelajuan sahaja tidak secara automatik menentukan dimensi yang betul bagi ruang ciri persekitaran. Jika dimensi ruang ciri terlalu rendah, model yang dipelajari akan kurang sesuai dengan data jika terlalu tinggi, model mungkin terlalu muat.

Pada pandangan mereka, matlamat persepsi adalah untuk mempelajari semua kandungan persepsi yang boleh diramal. Sistem pintar seharusnya dapat menjana semula pengedaran data yang diperhatikan daripada perwakilan termampat yang, setelah dijana, ia sendiri tidak dapat membezakan, tidak kira betapa sukarnya ia cuba. | Ketekalan diri sahaja tidak memastikan keuntungan dalam pemampatan atau kecekapan.

Secara matematik dan pengiraan, muatkan mana-mana data latihan menggunakan model terparameter berlebihan atau pastikan konsistensi dengan mewujudkan pemetaan satu sama satu antara domain dengan dimensi yang sama, sementara Ia mudah tanpa mempelajari struktur intrinsik dalam pengagihan data. Hanya melalui pemampatan sistem pintar boleh dipaksa untuk menemui struktur dimensi rendah intrinsik dalam data deria dimensi tinggi dan mengubah serta mewakili struktur ini dalam ruang ciri dengan cara yang paling padat untuk kegunaan masa hadapan.

Selain itu, hanya melalui pemampatan kita boleh memahami dengan mudah sebab penparameteran berlebihan, contohnya, seperti DNN biasanya melakukan peningkatan ciri melalui ratusan saluran, jika tujuan murninya adalah untuk melakukan pada Mampatan tinggi dalam ruang ciri dimensi tidak membawa kepada pemampatan berlebihan: rangsangan membantu mengurangkan ketaklinearan dalam data, menjadikannya lebih mudah untuk dimampatkan dan dilinearkan. Peranan lapisan seterusnya adalah untuk melakukan pemampatan (dan linearisasi), dan secara amnya lebih banyak lapisan, lebih baik pemampatan.

Dalam kes khas memampatkan kepada perwakilan berstruktur seperti LDR, kertas itu memanggil sejenis pengekodan automatik (lihat kertas asal untuk butiran) "transkripsi". Kesukaran di sini ialah menjadikan matlamat boleh dikendalikan secara pengiraan dan dengan itu boleh dicapai secara fizikal.

Pengurangan kadar ΔR memberikan ukuran jarak utama yang tidak jelas antara taburan yang merosot. Tetapi ia hanya berfungsi untuk subruang atau campuran Gaussians, bukan untuk pengedaran umum! Dan kita hanya boleh mengharapkan taburan perwakilan berstruktur dalaman z sebagai campuran subruang atau Gaussians, bukan data asal x.

Ini membawa kepada persoalan yang agak mendalam tentang mempelajari perwakilan "konsisten diri": untuk mengesahkan bahawa model dalaman dunia luaran adalah betul, sistem autonomi benar-benar perlu mengukur perbezaan dalam ruang data ?

Jawapannya tidak.

Kuncinya ialah menyedari bahawa untuk membandingkan x dan x^, ejen hanya perlu membandingkan ciri dalaman masing-masing z = f(x) dan z^ = melalui pemetaan yang sama f f (x^), untuk menjadikan z padat dan berstruktur.

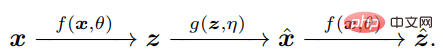
Mengukur perbezaan taburan dalam ruang-z sebenarnya ditakrifkan dengan baik dan cekap: boleh dikatakan bahawa dalam kecerdasan semula jadi, mempelajari perbezaan ukuran dalaman adalah autonomi bebas. sistem Satu-satunya perkara yang boleh dilakukan oleh otak.

Ini secara berkesan menjana sistem maklum balas "gelung tertutup", dengan keseluruhan proses ditunjukkan dalam Rajah 6.

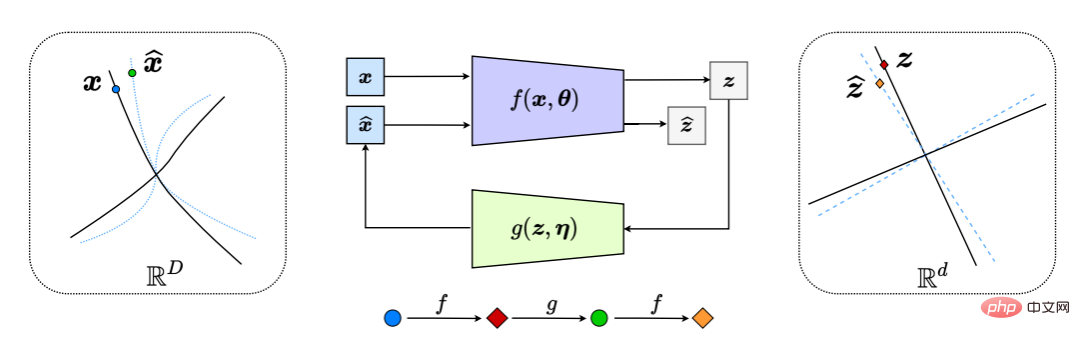
Rajah 6: Transkripsi gelung tertutup mampat submanifold data tak linear kepada LDR (dengan membandingkan dan meminimumkan perbezaan antara z dan z^ secara dalaman). Ini menghasilkan permainan kejar-mengejar semula jadi antara pengekod/sensor f dan penyahkod/pengawal g, supaya taburan x^ (garis putus-putus biru) yang dinyahkodkan mengejar dan sepadan dengan pengedaran data yang diperhatikan x (hitam garis pepejal).

Seseorang boleh mentafsir amalan popular mempelajari pengelas DNN f atau generator g secara berasingan sebagai mempelajari bahagian terbuka sistem gelung tertutup (Rajah 6). Pendekatan yang popular pada masa ini sangat serupa dengan kawalan gelung terbuka, yang telah lama diketahui oleh medan kawalan sebagai bermasalah dan mahal: latihan bahagian sedemikian memerlukan penyeliaan output yang diingini (seperti label kelas jika pengedaran data, sistem); parameter, atau tugas berlaku perubahan, penggunaan sistem gelung terbuka tersebut sememangnya tidak mempunyai kestabilan, keteguhan atau kebolehsuaian. Sebagai contoh, rangkaian pengelasan mendalam yang dilatih dalam persekitaran yang diselia sering mengalami pelupaan bencana jika dilatih semula untuk mengendalikan tugas baharu dengan kategori data baharu.

Sebaliknya, sistem gelung tertutup sememangnya lebih stabil dan adaptif. Malah, Hinton et al telah mencadangkan ini pada tahun 1995. Bahagian diskriminatif dan generatif perlu digabungkan masing-masing sebagai fasa "bangun" dan "tidur" proses pembelajaran yang lengkap.

Walau bagaimanapun, menutup gelung sahaja tidak mencukupi.

Makalah ini menyokong bahawa mana-mana ejen pintar memerlukan mekanisme permainan dalaman agar dapat belajar sendiri melalui kritikan diri! Apa yang berikut di sini ialah konsep permainan sebagai cara pembelajaran yang berkesan secara universal: berulang kali menggunakan model atau strategi semasa terhadap kritikan lawan, dengan itu terus menambah baik model atau strategi berdasarkan maklum balas yang diterima melalui gelung tertutup!

Dalam rangka kerja sedemikian, pengekod f memainkan peranan dwi: selain mempelajari perwakilan z data x dengan memaksimumkan pengurangan kadar ΔR(Z) (seperti yang dilakukan dalam Bahagian 2.1 itu), ia juga harus bertindak sebagai "sensor" maklum balas, secara aktif mengesan perbezaan antara data x dan x^ yang dijana. Penyahkod g juga memainkan peranan dwi: ia adalah pengawal, dikaitkan dengan perbezaan antara x dan ketepatan tertentu).

Oleh itu, tuple perwakilan "parsimonious" dan "konsisten diri" optimum (z, f, g) boleh ditafsirkan sebagai antara f(θ) dan g(η) Keseimbangan titik permainan jumlah sifar, dan bukannya utiliti berdasarkan pengurangan kadar gabungan:

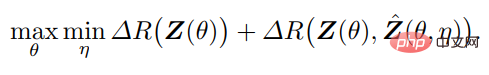
Perbincangan di atas ialah prestasi kedua-dua prinsip dalam keadaan yang diawasi.

Tetapi kertas kerja itu menekankan bahawa rangka kerja transkripsi gelung tertutup termampat yang mereka cadangkan mampu belajar sendiri melalui pemantauan kendiri dan kritikan kendiri!

Tambahan pula, memandangkan pengurangan kadar telah menemui perwakilan (jenis subruang) eksplisit untuk struktur pembelajaran, menjadikan pengetahuan lepas lebih mudah untuk dikekalkan apabila mempelajari tugasan/data baharu, ia boleh digunakan sebagai yang memelihara diri (ingatan) yang konsisten.

Karya empirikal terkini menunjukkan bahawa ini boleh menghasilkan sistem saraf serba lengkap pertama dengan ingatan tetap yang secara berperingkat boleh mempelajari perwakilan LDR yang baik tanpa mengalami pelupaan yang teruk. Untuk sistem gelung tertutup sedemikian, melupakan (jika ada) adalah agak elegan.

Selain itu, perwakilan yang dipelajari boleh disatukan lagi apabila imej kategori lama disalurkan kepada sistem sekali lagi untuk semakan—ciri yang hampir serupa dengan ingatan manusia. Dari satu segi, formulasi gelung tertutup yang terhad ini pada asasnya memastikan pembentukan memori visual boleh menjadi Bayesian dan adaptif-dengan mengandaikan ciri-ciri ini sesuai untuk otak.

Seperti yang ditunjukkan dalam Rajah 8, pengekodan automatik yang dipelajari bukan sahaja menunjukkan ketekalan sampel yang baik, tetapi ciri yang dipelajari juga mempamerkan struktur dimensi rendah (nipis ) tempatan yang jelas dan bermakna.

Rajah 8: Kiri: x lwn. Perbandingan antara x^ yang dinyahkod. Kanan: t-SNE ciri dipelajari tanpa pengawasan untuk 10 kelas, dan visualisasi beberapa kejiranan dan imej yang berkaitan dengannya. Perhatikan struktur nipis setempat (hampir satu dimensi) dalam ciri yang divisualisasikan, diunjurkan daripada ruang ciri ratusan dimensi.

Apa yang lebih mengejutkan ialah walaupun tiada maklumat kelas disediakan semasa latihan, subruang atau struktur pepenjuru blok berkaitan ciri mula muncul dalam ciri yang dipelajari untuk kelas ( Rajah 9 )! Oleh itu, struktur ciri yang dipelajari adalah serupa dengan kawasan selektif kategori yang diperhatikan dalam otak primata.

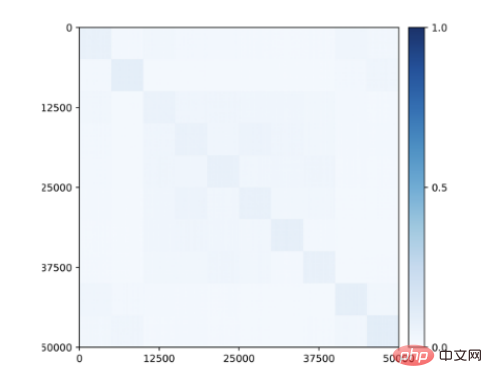
Rajah 9: Korelasi antara ciri dipelajari tanpa pengawasan untuk 50,000 imej yang tergolong dalam 10 kategori (CIFAR-10) melalui transkripsi gelung tertutup. Struktur pepenjuru blok konsisten kelas muncul tanpa sebarang pengawasan.

Enjin Pembelajaran Universal: Menggabungkan Penglihatan 3D dan Grafik

Ringkasan kertas, kesederhanaan dan ketekalan diri mendedahkan bahawa peranan rangkaian dalam adalah untuk menjadi gabungan pemerhatian luaran dan model pemetaan tak linear.

Di samping itu, kertas kerja menekankan bahawa struktur mampatan gelung tertutup ada di mana-mana dan boleh digunakan untuk semua makhluk pintar Ini boleh dilihat dalam otak (mampatan maklumat deria). litar saraf tunjang (mampatan pergerakan otot ), DNA (maklumat fungsi mampat protein), dan contoh biologi yang lain. Oleh itu, mereka percaya bahawa transkripsi gelung tertutup termampat mungkin merupakan enjin pembelajaran universal di sebalik semua tingkah laku pintar. Ia membolehkan organisma dan sistem pintar untuk menemui dan memperhalusi struktur berdimensi rendah daripada input yang kelihatan kompleks dan tidak teratur, dan menukarnya kepada struktur dalaman yang padat dan teratur yang boleh diingati dan digunakan.

Untuk menggambarkan keluasan rangka kerja ini, kertas kerja mengkaji dua tugas lain: persepsi 3D dan membuat keputusan (LeCun menganggap dua modul utama sistem pintar autonomi ini). Artikel ini disusun dan hanya memperkenalkan gelung tertutup penglihatan komputer dan grafik komputer dalam persepsi 3D.

Paradigma klasik visi 3D yang dicadangkan oleh David Marr dalam bukunya yang berpengaruh "Vision" menyokong pendekatan "pecah dan takluk", membahagikan tugas persepsi 3D kepada beberapa modul Proses: Dari rendah -pemprosesan 2D peringkat (cth. pengesanan tepi, lakaran kontur), penghuraian 2.5D peringkat pertengahan (cth. pengelompokan, pembahagian, bentuk dan tanah), kepada pembinaan semula 3D peringkat tinggi (cth. pose, bentuk) dan pengecaman (cth. objek), dan sebaliknya, Rangka kerja transkripsi gelung tertutup termampat menggalakkan idea "pembinaan bersama".

Persepsi ialah transkripsi gelung tertutup yang dimampatkan? Lebih tepat lagi, perwakilan 3D bagi bentuk, rupa dan juga dinamik objek di dunia seharusnya merupakan perwakilan paling padat dan tersusun yang dibangunkan secara dalaman oleh otak kita untuk mentafsir semua pemerhatian visual yang dirasakan dengan sewajarnya. Jika ya, maka kedua-dua prinsip ini mencadangkan bahawa perwakilan 3D yang padat dan berstruktur ialah model dalaman yang perlu dicari. Ini bermakna kita boleh dan harus menyatukan penglihatan komputer dan grafik komputer dalam rangka kerja pengkomputeran gelung tertutup, seperti yang ditunjukkan di bawah:

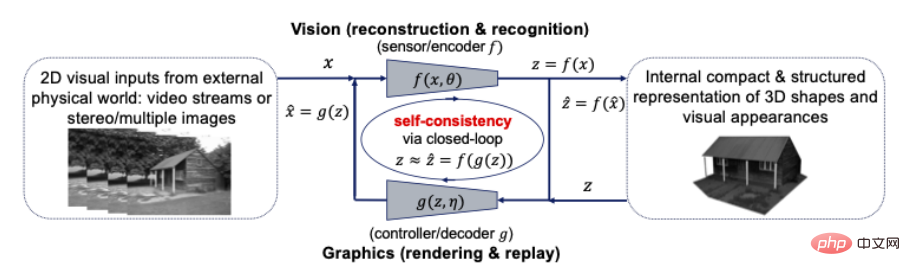
Rajah 10: Hubungan antara penglihatan komputer dan grafik Hubungan gelung tertutup untuk model 3D padat dan berstruktur untuk input visual

Penglihatan komputer sering diterangkan sebagai proses ke hadapan untuk membina semula dan mengenal pasti model 3D dalaman untuk semua input visual 2D, manakala grafik komputer mewakili proses songsang pemaparan dan menganimasikan model 3D dalaman. Menggabungkan kedua-dua proses ini secara terus ke dalam sistem gelung tertutup boleh membawa faedah pengiraan dan praktikal yang besar: semua struktur yang kaya dalam geometri, rupa visual dan dinamik (seperti kesederhanaan dan kelancaran) boleh digunakan bersama dalam model 3D bersatu, yang paling padat dan konsisten dengan semua input visual.

Teknik pengecaman dalam penglihatan komputer boleh membantu grafik komputer membina model padat dalam bentuk dan ruang rupa serta menyediakan cara baharu untuk mencipta kandungan 3D yang realistik. Sebaliknya, pemodelan 3D dan teknik simulasi dalam grafik komputer boleh meramal, mempelajari dan mengesahkan sifat dan tingkah laku objek dan pemandangan sebenar yang dianalisis oleh algoritma penglihatan komputer. Komuniti visual dan grafik telah lama mengamalkan pendekatan "analisis sintetik".

Perwakilan seragam rupa dan bentuk? Penyajian berasaskan imej, di mana pandangan baharu dijana dengan belajar daripada set imej yang diberikan, boleh dilihat sebagai percubaan awal untuk merapatkan jurang antara penglihatan dan grafik dengan prinsip perit dan konsisten diri. Khususnya, pensampelan plenoptik menunjukkan bahawa imej anti-alias (konsistensi diri) boleh dicapai dengan bilangan minimum imej yang diperlukan (parsimony).

Kecerdasan Yang Lebih Luas

Sains Neurosains Kecerdasan

Seseorang akan mengharapkan prinsip kecerdasan asas untuk memaklumkan reka bentuk otak telah impak yang ketara. Prinsip parsimoni dan ketekalan diri memberi penerangan baharu pada beberapa pemerhatian eksperimen sistem visual primata. Lebih penting lagi, mereka mendedahkan perkara yang perlu dicari dalam percubaan masa depan.

Pasukan pengarang telah menunjukkan bahawa hanya mencari perwakilan dalaman yang parsimoni dan ramalan sudah memadai untuk mencapai "penyeliaan diri", membolehkan struktur muncul secara automatik dalam perwakilan akhir yang dipelajari melalui gelung tertutup yang dimampatkan transkripsi.

Sebagai contoh, Rajah 9 menunjukkan bahawa pembelajaran transkripsi data tanpa pengawasan secara automatik membezakan ciri-ciri kategori yang berbeza, memberikan penjelasan untuk perwakilan selektif kategori yang diperhatikan dalam otak. Ciri-ciri ini juga memberikan penjelasan yang munasabah untuk pemerhatian meluas pengekodan jarang dan pengekodan subruang dalam otak primata. Tambahan pula, sebagai tambahan kepada pemodelan data visual, penyelidikan neurosains baru-baru ini mencadangkan bahawa perwakilan berstruktur lain yang timbul dalam otak (seperti "sel tempat") mungkin juga hasil pengekodan maklumat spatial dengan cara yang paling termampat.

Boleh dikatakan bahawa prinsip pengurangan kadar pengekodan maksimum (MCR2) adalah serupa dengan semangat "prinsip pengurangan tenaga bebas" dalam sains kognitif, yang cuba Menyediakan rangka kerja untuk Bayesian inferens melalui pengurangan tenaga. Tetapi tidak seperti konsep umum tenaga bebas, pengurangan kadar boleh dikendalikan secara pengiraan dan boleh dioptimumkan secara langsung kerana ia boleh dinyatakan dalam bentuk tertutup. Tambahan pula, interaksi kedua-dua prinsip ini menunjukkan bahawa pembelajaran autonomi model (kelas) yang betul harus dicapai melalui permainan memaksimumkan gelung tertutup utiliti ini, dan bukannya meminimumkan sahaja. Oleh itu, mereka percaya bahawa rangka kerja transkripsi gelung tertutup termampat memberikan perspektif baharu tentang cara inferens Bayesian boleh dilaksanakan secara praktikal.

Rangka kerja ini juga dipercayai oleh mereka untuk menjelaskan keseluruhan seni bina pembelajaran yang digunakan oleh otak, yang boleh membina segmen suapan ke hadapan dengan membuka skema pengoptimuman tanpa perlu belajar daripada rangkaian rawak melalui perambatan balik . Di samping itu, terdapat bahagian generatif pelengkap bagi rangka kerja yang boleh membentuk sistem maklum balas gelung tertutup untuk membimbing pembelajaran.

Akhir sekali, rangka kerja mendedahkan isyarat "ralat ramalan" yang sukar difahami yang dicari oleh ramai saintis saraf yang berminat dengan mekanisme otak "pengekodan ramalan", sejenis transkripsi gelung tertutup yang berkaitan dengan mampatan Pengiraan skema untuk menjana resonans: Untuk memudahkan pengiraan, perbezaan antara pemerhatian masuk dan pemerhatian yang dijana hendaklah diukur pada peringkat akhir perwakilan.

Ke arah tahap kecerdasan yang lebih tinggi

Karya Ma Yi et al percaya bahawa transkripsi gelung tertutup mampat adalah serupa dengan yang dicadangkan oleh Hinton et al pada tahun 1995 Berbanding dengan rangka kerja lain, ia adalah lebih mudah untuk diproses dan berskala. Selain itu, pembelajaran berulang pemetaan pengekodan/penyahkodan tak linear (selalunya dimanifestasikan sebagai rangkaian dalam) pada asasnya menyediakan jambatan penting antara data deria mentah luaran yang tidak teratur (seperti penglihatan, pendengaran, dll.) dan "antara muka" dalaman.

Walau bagaimanapun, mereka juga menegaskan bahawa kedua-dua prinsip ini tidak semestinya menjelaskan semua aspek kecerdasan. Mekanisme pengiraan yang mendasari kemunculan dan perkembangan penaakulan semantik, simbolik atau logik peringkat tinggi kekal sukar difahami. Sehingga hari ini, terdapat perdebatan sama ada kecerdasan simbolik lanjutan ini boleh timbul daripada pembelajaran berterusan atau mesti dikodkan secara keras.

Pada pandangan ketiga-tiga saintis, perwakilan dalaman berstruktur seperti subruang adalah langkah perantaraan yang diperlukan untuk kemunculan konsep semantik atau simbolik peringkat tinggi - setiap subruang sepadan dengan diskret ( objek) kategori. Perhubungan statistik, sebab atau logik lain antara konsep diskret abstrak tersebut boleh dipermudahkan dan dimodelkan sebagai graf padat dan berstruktur (mis. jarang), dengan setiap nod mewakili subruang/kategori. Graf boleh dipelajari melalui pengekodan automatik untuk memastikan ketekalan diri.

Mereka membuat spekulasi bahawa kemunculan dan perkembangan kecerdasan lanjutan (dengan pengetahuan simbolik yang boleh dikongsi) hanya mungkin di atas perwakilan yang padat dan berstruktur yang dipelajari oleh ejen individu. Oleh itu, mereka mencadangkan bahawa prinsip baru untuk kemunculan kecerdasan maju (jika kecerdasan maju wujud) harus diterokai melalui pertukaran maklumat atau pemindahan pengetahuan yang berkesan antara sistem pintar.

Tambahan pula, kecerdasan peringkat tinggi harus mempunyai dua persamaan dengan dua prinsip yang kami cadangkan dalam artikel ini:

• Kebolehtafsiran: Semua Prinsip harus semuanya membantu untuk mendedahkan mekanisme pengiraan pintar sebagai kotak putih, termasuk matlamat yang boleh diukur, seni bina pengiraan yang berkaitan dan struktur untuk perwakilan pembelajaran.
• Kebolehkiraan: Mana-mana prinsip kecerdasan baharu mestilah boleh dikendalikan dan berskala secara pengiraan, boleh dicapai oleh komputer atau fizik semula jadi, dan akhirnya disahkan oleh bukti saintifik.

Hanya dengan kebolehtafsiran dan kebolehkiraan kita boleh memajukan kemajuan kecerdasan buatan tanpa bergantung pada kaedah "percubaan dan kesilapan" semasa yang mahal dan memakan masa serta dapat menerangkan dan lengkapkan ini Data minimum dan sumber pengkomputeran yang diperlukan untuk tugas itu, dan bukannya hanya menyokong pendekatan kekerasan "lebih besar adalah lebih baik". Kebijaksanaan tidak seharusnya menjadi hak prerogatif orang yang paling bijak Dengan set prinsip yang betul, sesiapa sahaja harus dapat mereka bentuk dan membina sistem pintar generasi akan datang, besar atau kecil, yang autonomi, keupayaan, dan kecekapannya akhirnya boleh meniru atau bahkan. mengatasi haiwan dan manusia.

Pautan kertas:

​https://arxiv.org/pdf/2207.04630.pdf​

Atas ialah kandungan terperinci Jangan mengejar model besar secara membabi buta dan mengumpul kuasa pengkomputeran! Shen Xiangyang, Cao Ying dan Ma Yi mencadangkan dua prinsip asas untuk memahami AI: parsimoni dan konsistensi diri. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!