Bagaimana untuk mengisih 100 juta nombor rawak di Jawa?

1. Isih sisipan langsung

1. Isih sisipan bergambar

Idea: Secara harfiah, sisipan ialah meletakkan elemen ke tempat tertentu mengikut peraturan tertentu. dalam set, jadi kita perlu membahagikan urutan itu kepada dua bahagian, satu bahagian ialah set tersusun, dan bahagian lain ialah set yang hendak diisih

Ilustrasi:

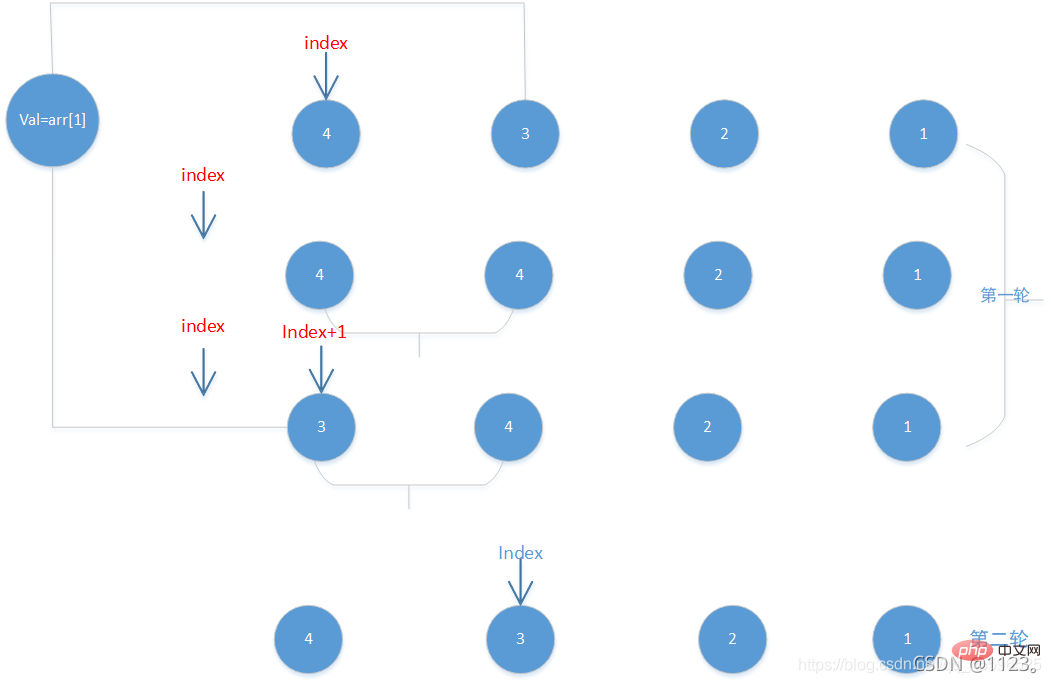
Untuk memudahkan pemahaman, kami akan mengambil urutan 4321 yang paling istimewa sebagai contoh

Mengikut idea di atas, kita perlu membahagikan urutan tersebut kepada dua bahagian. . Untuk kemudahan pengekodan, kami akan membahagikan yang pertama kepada dua bahagian dengan mengandaikan bahawa elemen adalah set tersusun, maka gelung kami harus bermula dari elemen kedua , iaitu 3

Untuk mengelak daripada menulis ganti 3 dalam operasi seterusnya, kami memilih Pembolehubah sementara untuk menyimpan 3. Iaitu, val=arr[1] di atas,

Memandangkan kami beroperasi pada tatasusunan, kami juga perlu mendapatkan indeks elemen terakhir yang dipesan ditetapkan sebagai kursor

Apabila kursor tidak melintasi sempadan dan nilai yang hendak disisipkan adalah kurang daripada kedudukan yang ditunjukkan oleh kursor (4 dalam gambar di atas), kita gerakkan elemen 4 ke belakang, gerakkan kursor ke hadapan, dan terus semak koleksi Adakah elemen lain dalam set lebih kecil daripada elemen yang akan dimasukkan, sehingga kursor melintasi sempadan

Dalam angka di atas, kerana terdapat hanya satu 4 dalam set, kursor bergerak ke hadapan dan melintasi sempadan, jadi gelung itu berakhir

public static void insertSort(int[]arr){
        for(int i = 1 ; i < arr.length; i++){
            int val = arr[i];
            int valIndex = i - 1; //游标
            while(valIndex >= 0 && val < arr[valIndex]){ //插入的值比游标指示的值小
                arr[valIndex + 1] = arr[valIndex];
                valIndex--; //游标前移
            }
            arr[valIndex+1] = val;
        }
    }
1234567891011

3. Ujian prestasi dan kerumitan ruang masa

Ia sebenarnya mengambil masa 1 minit dan 4 saat untuk menjalankan 800,000 keping data (bukan nilai yang tepat, setiap mesin mungkin berbeza) )Bilangan perbandingan kata kunci:

Jumlah bilangan pergerakan:

Jadi kerumitan masa adalah kira-kira

2. Isih bukit ( kaedah pertukaran)

1. Ilustrasi idea

KCN=(n^2)/2RMN= (n^2)/22. Pelaksanaan kod

public static void shellSort(int[] arr){ //交换法
        int tmp = 0;
        for(int gap = arr.length / 2 ; gap > 0 ; gap /= 2){
            for(int i = gap ; i < arr.length ; i++){ //先遍历所有数组
                for(int j  = i - gap ; j >= 0 ; j -= gap){//开启插入排序
                    if(arr[ j ] > arr[ gap + j ]){ //可以根据升降序修改大于或小于
                        tmp = arr[gap + j];
                        arr[j+gap] = arr[j];
                        arr[j] = tmp;
                    }
                }
            }
            System.out.println(gap);
            System.out.println(Arrays.toString(arr));
        }
    }
12345678910111213141516

Perkara yang paling sukar untuk difahami di sini ialah yang ketiga untuk Gelung, O(N^2), mewakili elemen pertama dalam kumpulan, iaitu,

,

apabila elemen pertama dalam kumpulan lebih besar daripada elemen kedua (

ialah klasifikasi logik , indeks bagi elemen kedua hendaklah semua nilai elemen pertama + jurang tambahan

), tukar dua, jika tidak

, teruskan membandingkan atau melompat keluar dari gelung,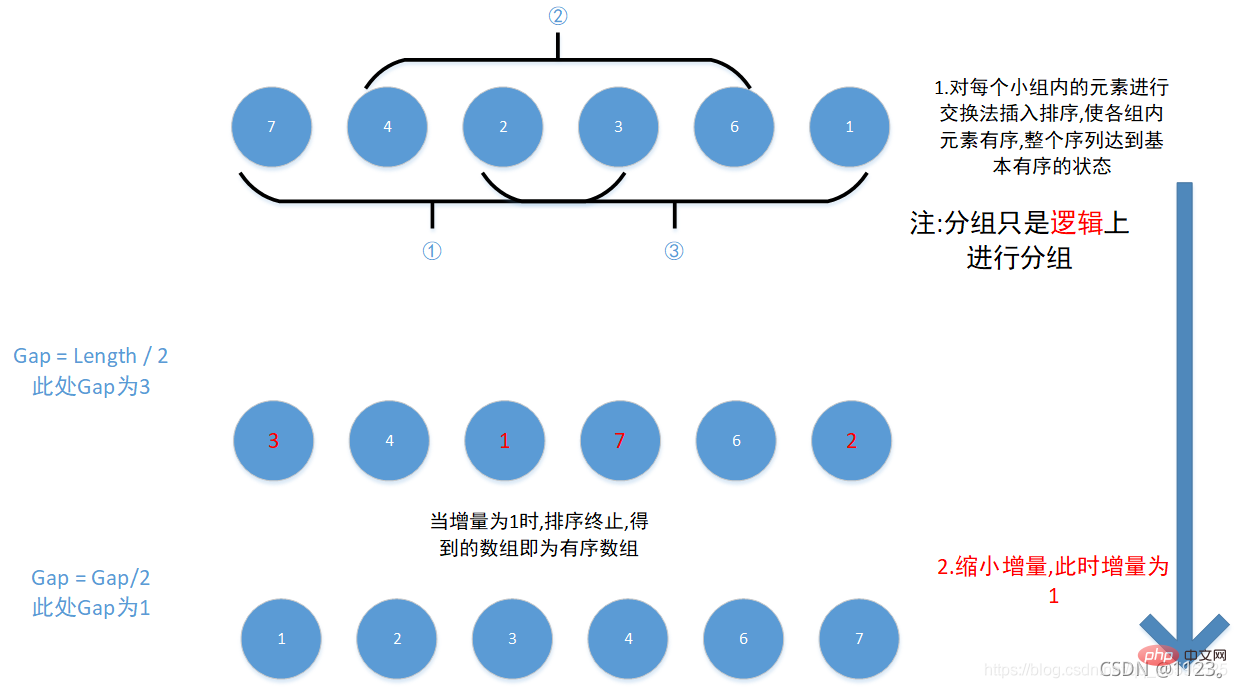

dan sebagainya hidup, semua Selepas semua kumpulan telah merentasi, kurangkan kenaikan (iaitu

), dan kemudian teruskan langkah di atas sehingga jurang kenaikan ialah 1, pengisihan jujukan tamat

3 Kerumitan masa j = i - gapj=0H Kerumitan masa pengisihan Er bergantung pada fungsi

jujukan tambahan

, yang memerlukan analisis khusus masalah khusus dan bukan nilai yang pasti Ini juga merupakan perkara keempat yang perlu dibincangkan 4 pemilihan kenaikan, Ia adalah masalah yang tidak dapat diselesaikan dalam matematik j-=gap

, tetapi apa yang pasti ialah melalui sejumlah besar eksperimen, telah terbukti bahawa apabila

, kerumitan masa boleh dikurangkan kepada: gap/=2

Dalam perkara seterusnya, dalam kaedah anjakan, kami juga telah melakukan beberapa eksperimen Kami boleh memastikan bahawa untuk pengiraan dalam skala tertentu (. seperti 800w~100 juta),

Bukit Kelajuan pengisihan jauh lebih cepat daripada pengisihan timbunan

, sekurang-kurangnya pada komputer saya

3. Pengisihan bukit (kaedah anjakan) Kaedah pertukaran lebih cepat daripada kaedah anjakan Kaedah bit adalah jauh lebih perlahan, jadi kaedah anjakan gap/=2 lebih biasa digunakan, dan kaedah anjakan lebih "seperti" jenis sisipan

1. Berbanding dengan kaedah swap, kaedah anjakan n->无穷大

Idea sebenarnya adalah gabungan dua pengisihan di atas menggabungkan kelebihan

pengumpulan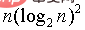 dan

menyisipkan

. . Kecekapan adalah sangat tinggi. merangkumi mata. >2. Pelaksanaan kod

public static void shellSort02(int[] arr){ //移位法
        for(int gap = arr.length/2 ; gap > 0 ; gap /= 2){ //分组
            for(int i = gap ; i < arr.length ; i++){ //遍历
                int valIndex = i;
                int val = arr[valIndex];
                if(val < arr[valIndex-gap]){ //插入的值小于组内另一个值
                   while(valIndex - gap >=0 && val < arr[valIndex-gap]){ //开始插排
                       // 插入
                       arr[valIndex] = arr[valIndex-gap];
                       valIndex -= gap; //让valIndex = valIndex-gap (游标前移)
                   }
                }
                arr[valIndex] = val;
            }
        }
    }
12345678910111213141516

3.

Atas ialah kandungan terperinci Bagaimana untuk mengisih 100 juta nombor rawak di Jawa?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!