Bagaimana untuk menggunakan Python untuk melaksanakan algoritma genetik untuk menyelesaikan Masalah Jurujual Perjalanan (TSP)?

Masalah TSP

Jadi sebelum kita mulakan, mari kita huraikan masalah TSP ini secara terperinci. Rakan-rakan yang telah melakukan pemodelan digital, atau telah didedahkan kepada pengoptimuman pintar atau pembelajaran mesin semua harus mengetahui perkara ini. Sudah tentu, demi khalayak sejagat artikel ini, kami akan cuba yang terbaik untuk menjadikannya sesempurna dan sejelas mungkin. di sini, supaya kita dapat menyelesaikan masalah tersebut.

Maka masalahnya sebenarnya mudah, ia kelihatan seperti ini:

Dalam satah N-dimensi kami, hari ini kami menggunakan satah dua dimensi ini Ayuh , terdapat banyak bandar dalam pesawat ini, dan bandar-bandar itu bersambung antara satu sama lain Sekarang kita perlu mencari jalan terpendek untuk melawat semua bandar. Sebagai contoh kita mempunyai bandar A, B, C, D, E. Sekarang setelah kita mengetahui koordinat antara bandar, yang bersamaan dengan mengetahui jarak antara bandar, kita kini boleh mencari jujukan yang boleh membuat laluan terpendek ke semua bandar A, B, C, D dan E. Sebagai contoh, selepas pengiraan, ia mungkin B-->A-->C-->E-->D. Dengan kata lain, cari pesanan ini.

Enumeration

Kalau kita nak selesaikan dulu masalah ni, sebenarnya banyak penyelesaiannya, kita cuma perlu cari order yang boleh minimize the sum of paths, so the yang paling mudah untuk difikirkan ialah Sememangnya, ia adalah penghitungan Sebagai contoh, biarkan A pergi dahulu dan kemudian lihat jika yang terdekat dengan A ialah B, kemudian pergi ke B, dan kemudian pergi dari B. Sudah tentu, ini adalah strategi tamak tempatan, dan ia mudah untuk mencapai optimum tempatan Kemudian kita boleh mempertimbangkan DP pada masa ini, iaitu, kita masih menganggap bahawa kita bermula dari A, dan kemudian memastikan bahawa 2 bandar adalah. yang terpendek, 3 bandar adalah yang terpendek, dan 4 dan 5 adalah yang terpendek. Akhirnya, anggap perkara yang sama dari B. Atau hitung terus semua situasi dan hitung jaraknya. Tetapi tidak kira apa, apabila bilangan bandar bertambah, kerumitannya akan meningkat, jadi pada masa ini kita perlu mencari cara untuk menjadikan pengkomputeran menggunakan kepakaran manusia kita. Saya memanggilnya "buta".

Algoritma Pintar

Sekarang mari kita bincangkan tentang algoritma pintar ini dan mengapa ia digunakan tidak semestinya begitu. Jadi pada masa ini, pertama sekali, untuk masalah TSP sahaja, apa yang kita mahu adalah urutan, urutan yang tidak akan berulang. Jadi pada masa ini, adakah terdapat penyelesaian yang lebih mudah Dan apabila data cukup besar, kita tidak semestinya memerlukan penyelesaian yang tepat dan minima sepenuhnya, selagi ia hampir. Jadi pada masa ini, jika kita menggunakan algoritma tradisional, satu adalah satu Ia hanya akan mengira mengikut peraturan kita, dan kita benar-benar tidak tahu apa jawapan standard Ia juga sukar untuk menetapkan ambang untuk menghentikan pengiraan algoritma tradisional. Tapi bagi kita orang, ada yang namanya "tuah". Jadi algoritma pintar kami sebenarnya agak serupa dengan "Monyet". Tetapi orang memberi perhatian kepada kemahiran Sebagai contoh, pengalaman memberitahu kita bahawa tiga panjang dan satu pendek Anda boleh menggunakan teknik ini untuk meneka jawapannya. anda hanya memerlukan sekeping 40 siri (30 juga okey) Kad grafik boleh diambil dengan mudah. Meng perlukan kemahiran, kami panggil strategi ini.

Strategi

Jadi teknik yang kita cakap tadi, helah ini. Dalam algoritma pintar, topeng ini adalah salah satu strategi kami. Bagaimanakah kita boleh menyingkirkannya supaya penyelesaian kita boleh menjadi lebih munasabah? Kemudian pada masa ini, seratus bunga akan mekar saya tidak akan melaungkan sutra di sini Mari kita ambil dua algoritma yang paling klasik sebagai contoh, satu adalah algoritma genetik dan satu lagi algoritma kumpulan zarah (PSO). Sebagai contoh, mereka menggunakan strategi untuk menyahsulit, seperti algoritma genetik Dengan mensimulasikan pemilihan semula jadi, mereka mula-mula menghasilkan sekumpulan penyelesaian dan sekumpulan jujukan, dan kemudian berdasarkan strategi pemilihan semula jadi kami, dan kemudian gunakan penyelesaian ini untuk mencari penyelesaian baharu dan lebih baik. Selepas berulang alik begini, akhirnya saya mendapat penyelesaian yang baik. Kumpulan zarah adalah serupa Kami akan menerangkan bahagian ini secara terperinci apabila kami menggunakannya.

Algoritma

Sekarang kita tahu strategi ini, apakah algoritma ini sebenarnya adalah langkah untuk melaksanakan strategi ini, iaitu kod kita, gelung dan struktur data. Kita perlu sedar apa yang baru kita nyatakan, seperti pemilihan semula jadi, seperti TSP kita, cara menjana sekumpulan penyelesaian secara rawak.

Sampel Data

ok, kita telah selesai bercakap tentang beberapa konsep asas di sini, jadi pada masa ini, mari kita lihat bagaimana kita mewakili masalah TSP ini sebenarnya sangat mudah. bagi kami di sini kami hanya menyediakan data ujian. Kami menganggap terdapat 14 bandar di sini, maka data kami untuk bandar-bandar ini adalah seperti berikut:

    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))

Kami akan menggunakan set data ini untuk ujian kemudian, sekarang di atas Terdapat sudah 14 bandar.

Kemudian mari kita mulakan penyelesaian kami

Algoritma Genetik

ok, kemudian mari kita bincangkan tentang algoritma genetik kita, kita gunakan ini untuk menyelesaikan masalah TSP ini.

Jadi sekarang, mari kita lihat bagaimana algoritma genetik kita ditipu.

算法流程

遗传算法其实是在用计算机模拟我们的物种进化。其实更加通俗的说法是筛选，这个就和我们袁老爷爷种植水稻一样。有些个体发育良好，有些个体发育不好，那么我就先筛选出发育好的，然后让他们去繁衍后代，然后再筛选，最后得到高产水稻。其实也和我们社会一样，不努力就木有女朋友就不能保留自己的基因，然后剩下的人就是那些优秀的人和富二代的基因，这就是现实呀。所以得好好学习，天天向上！

那么回到主题，我们的遗传算法就是在模拟这一个过程，模拟一个物竞天择的过程。

所以在我们的算法里面也是分为几大块

繁殖

首先我们的种群需要先繁殖。这样才能不断产生优良基于，那么对应我们的算法，假设我们需要求取

Y = np.sin(10 * x) * x + np.cos(2 * x) * x

的最大值（在一个范围内）那么我们的个体就是一组（X1）的解。好的个体就会被保留，不好的就会被pass，选择标准就是我们的函数 Y 。那么问题来了如何模拟这个过程？我们都知道在繁殖后代的时候我们是通过DNA来保留我们的基因信息，在这个过程当中，父母的DNA交互，并且在这个过程当中会产生变异，这样一来，父母双方的优秀基于会被保存，并且产生的变异有可能诞生更加优秀的后代。

所以接下来我们需要模拟我们的ＤＮＡ，进行交叉和变异。

交叉

这个交叉过程和我们的生物其实很像，当然我们在我们的计算机里面对于数字我们可以将其转化为二进制，当做我们的DNA

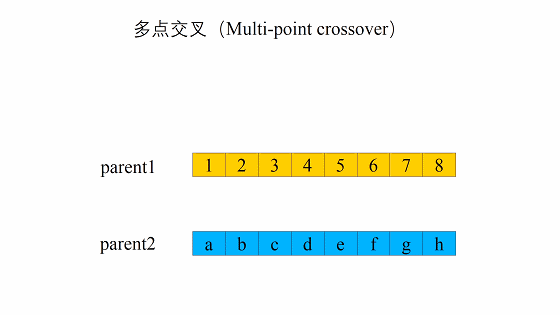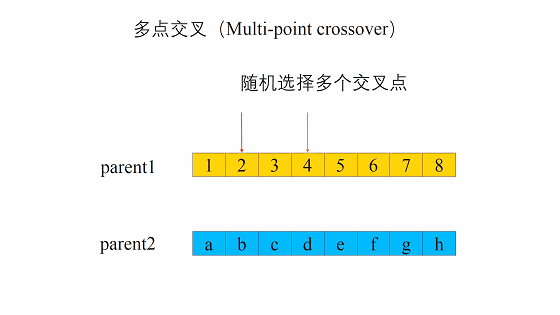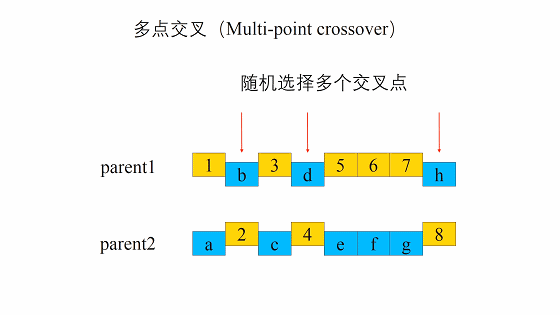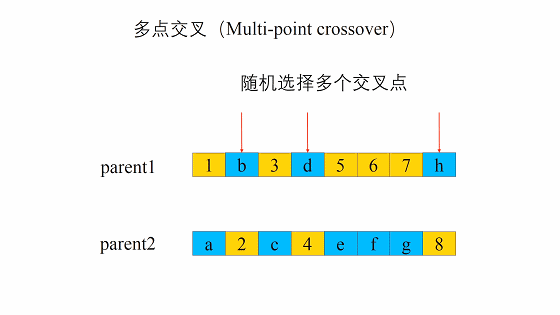
交叉的方式有很多，我们这边选择这一个，进行交叉。

变异

那这个在我们这里就更加简单了

我们只需要在交叉之后，再随机选择几个位置进行改变值就可以了。当然变异的概率是很小的，并且是随机的，这一点要注意。并且由于变异是随机的，所以不排除生成比原来还更加糟糕的个体。

选择

最后我们按照一定的规则去筛选这个些个体就可以了，然后淘汰原来的个体。那么在我们的计算机里面是使用了两个东西，首先我们要把原来二进制的玩意，给转化为我们原来的十进制然后带入我们的函数运算，然后保存起来，之后再每一轮统一筛选一下就好了。

逆转

这个咋说呢，说好听点叫逆转，难听点就算，对于一些新的生成的不好的解，我们是要舍弃的。

代码

那么这部分用代码描述的话就是这样的：

import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
    '''
    目标函数，需要被优化的函数
    :param x:
    :return:
    '''
    return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
    '''
    交叉DNA，我们直接在种群里面选择一个交配
    然后就生出孩子了
    :param parent:
    :param PopSpace:
    :return:
    '''
    if(np.random.rand()) < Cross_Rate:
        cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
        cross_one = np.random.randint(0, Population_Size, size=1) #选择一位男/女士交配
        Parent[cross_place] = PopSpace[cross_one,cross_place]
    return Parent
def Mutate(Child):
    &#39;&#39;&#39;
    变异
    :param Child:
    :return:
    &#39;&#39;&#39;
    for point in range(Dna_Size):
        if np.random.rand() < Mutation_Rate:
            Child[point] = 1 if Child[point] == 0 else 0
    return Child
def TranslateDNA(PopSpace):
    &#39;&#39;&#39;
    把二进制转化为十进制方便计算
    :param PopSpace:
    :return:
    &#39;&#39;&#39;
    return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
    &#39;&#39;&#39;
    这个其实是对我们得到的F(x)进行换算，其实就是选择的时候
    的概率，我们需要处理负数，因为概率不能为负数呀
    pred 这是一个二维矩阵
    :param pred:
    :return:
    &#39;&#39;&#39;
    return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
    &#39;&#39;&#39;
    选择
    :param PopSpace:
    :param Fitness:
    :return:
    &#39;&#39;&#39;
    &#39;&#39;&#39;
    这里注意的是，我们先按照权重去选择我们的优良个体，所以我们这里选择的时候允许重复的元素出现
    之后我们就可以去掉这些重复的元素，这样才能实现保留良种去除劣种。100--》70（假设有30个重复）
    如果不允许重复的话，那你相当于没有筛选
    &#39;&#39;&#39;
    Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
                           p=Fitness / Fitness.sum())
    # np.unique(Better_Ones) #这个是我后面加的
    return PopSpace[Better_Ones]
if __name__ == &#39;__main__&#39;:
    PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size))  # initialize the PopSpace DNA
    plt.ion() 
    x = np.linspace(X_Range, 200)
    # plt.plot(x, F(x))
    plt.xticks([0,10])
    plt.yticks([0,10])
    for _ in range(Iteration_Number):
        F_values = F(TranslateDNA(PopSpace))  
        # something about plotting
        if &#39;sca&#39; in globals():
            sca.remove()
        sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c=&#39;red&#39;, alpha=0.5)
        plt.pause(0.05)
        # GA part (evolution)
        fitness = Fitness(F_values)
        print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
        PopSpace = Select(PopSpace, fitness)
        PopSpace_copy = PopSpace.copy()
        for parent in PopSpace:
            child = CrossOver(parent, PopSpace_copy)
            child = Mutate(child)
            parent[:] = child
    plt.ioff()
    plt.show()

这个代码是以前写的，逆转没有写上（下面的有）

TSP遗传算法

ok,刚刚的例子是拿的解方程，也就是说是一个连续问题吧，当然那个连续处理的话并不是很好，只是一个演示。那么我们这个的话其实类似的。首先我们的ＤＮＡ，是城市的路径，也就是A-B-C-D等等，当然我们用下标表示城市。

种群表示

首先我们确定了使用城市的序号作为我们的个体DNA，例如咱们种群大小为100，有ＡＢＣＤ四个城市，那么他就是这样的，我们先随机生成种群，长这个样：

1 2 3 4
2 3 4 5
3 2 1 4
...

那个1,2,3,4是ABCD的序号。

交叉与变异

这里面的话，值得一提的就是，由于暂定城市需要是不能重复的，且必须是完整的，所以如果像刚刚那样进行交叉或者变异的话，那么实际上会出点问题，我们不允许出现重复，且必须完整，对于我们的DNA，也就是咱们瞎蒙的个体。

代码

由于咱们每一步在代码里面都有注释，所以的话咱们在这里就不再进行复述了。

from math import floor
import numpy as np
import matplotlib.pyplot as plt
class Gena_TSP(object):
    """
    使用遗传算法解决TSP问题
    """
    def __init__(self, data, maxgen=200,
                 size_pop=200, cross_prob=0.9,
                 pmuta_prob=0.01, select_prob=0.8
                 ):
        self.maxgen = maxgen            # 最大迭代次数
        self.size_pop = size_pop        # 群体个数，（一次性瞎蒙多少个解）
        self.cross_prob = cross_prob    # 交叉概率
        self.pmuta_prob = pmuta_prob    # 变异概率
        self.select_prob = select_prob  # 选择概率
        self.data = data        # 城市的坐标数据
        self.num = len(data)    # 有多少个城市，对应多少个坐标，对应染色体的长度（我们的解叫做染色体）
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()
        self.select_num = int(self.size_pop * self.select_prob)
        # 通过选择概率确定子代的选择个数
        """
        初始化子代和父代种群，两者相互交替
        """
        self.parent = np.array([0] * self.size_pop * self.num).reshape(self.size_pop, self.num)
        self.child = np.array([0] * self.select_num * self.num).reshape(self.select_num, self.num)
        """
        负责计算每一个个体的（瞎蒙的解）最后需要多少距离
        """
        self.fitness = np.zeros(self.size_pop)
        self.best_fit = []
        self.best_path = []
        # 保存每一步的群体的最优路径和距离
    def __matrix_dis(self):
        """
        计算14个城市的距离，将这些距离用矩阵存起来
        :return: 
        """
        res = np.zeros((self.num, self.num))
        for i in range(self.num):
            for j in range(i + 1, self.num):
                res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
                res[j, i] = res[i, j]
        return res
    def rand_parent(self):
        """
        初始化种群
        :return:
        """
        rand_ch = np.array(range(self.num))
        for i in range(self.size_pop):
            np.random.shuffle(rand_ch)
            self.parent[i, :] = rand_ch
            self.fitness[i] = self.comp_fit(rand_ch)
    def comp_fit(self, one_path):
        """
        计算，咱们这个路径的长度，例如A-B-C-D
        :param one_path:
        :return:
        """
        res = 0
        for i in range(self.num - 1):
            res += self.__matrix_distance[one_path[i], one_path[i + 1]]
        res += self.__matrix_distance[one_path[-1], one_path[0]]
        return res
    def out_path(self, one_path):
        """
        输出我们的路径顺序
        :param one_path:
        :return:
        """
        res = str(one_path[0] + 1) + '-->'
        for i in range(1, self.num):
            res += str(one_path[i] + 1) + '-->'
        res += str(one_path[0] + 1) + '\n'
        print(res)
    def Select(self):
        """
        通过我们的这个计算的距离来计算出概率，也就是当前这些个体DNA也就瞎蒙的解
        之后我们在通过概率去选择个体，放到child里面
        :return:
        """
        fit = 1. / (self.fitness)  # 适应度函数
        cumsum_fit = np.cumsum(fit)
        pick = cumsum_fit[-1] / self.select_num * (np.random.rand() + np.array(range(self.select_num)))
        i, j = 0, 0
        index = []
        while i < self.size_pop and j < self.select_num:
            if cumsum_fit[i] >= pick[j]:
                index.append(i)
                j += 1
            else:
                i += 1
        self.child = self.parent[index, :]
    def Cross(self):
        """
        模仿DNA交叉嘛，就是交换两个瞎蒙的解的部分的解例如
        A-B-C-D
        C-D-A-B
        我们选几个交叉例如这样
        A-D-C-B
        1,3号交换了位置，当然这里注意可不能重复啊
        :return:
        """
        if self.select_num % 2 == 0:
            num = range(0, self.select_num, 2)
        else:
            num = range(0, self.select_num - 1, 2)
        for i in num:
            if self.cross_prob >= np.random.rand():
                self.child[i, :], self.child[i + 1, :] = self.intercross(self.child[i, :],
                                                                             self.child[i + 1, :])
    def intercross(self, ind_a, ind_b):
        """
        这个是我们两两交叉的具体实现
        :param ind_a:
        :param ind_b:
        :return:
        """
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        ind_a1 = ind_a.copy()
        ind_b1 = ind_b.copy()
        for i in range(left, right + 1):
            ind_a2 = ind_a.copy()
            ind_b2 = ind_b.copy()
            ind_a[i] = ind_b1[i]
            ind_b[i] = ind_a1[i]
            x = np.argwhere(ind_a == ind_a[i])
            y = np.argwhere(ind_b == ind_b[i])
            if len(x) == 2:
                ind_a[x[x != i]] = ind_a2[i]
            if len(y) == 2:
                ind_b[y[y != i]] = ind_b2[i]
        return ind_a, ind_b
    def Mutation(self):
        """
        之后是变异模块，这个就是按照某个概率，去替换瞎蒙的解里面的其中几个元素。
        :return:
        """
        for i in range(self.select_num):
            if np.random.rand() <= self.cross_prob:
                r1 = np.random.randint(self.num)
                r2 = np.random.randint(self.num)
                while r2 == r1:
                    r2 = np.random.randint(self.num)
                self.child[i, [r1, r2]] = self.child[i, [r2, r1]]
    def Reverse(self):
        """
        近化逆转，就是说下一次瞎蒙的解如果没有更好的话就不进入下一代，同时也是随机选择一个部分的
        我们不是一次性全部替换
        :return: 
        """
        for i in range(self.select_num):
            r1 = np.random.randint(self.num)
            r2 = np.random.randint(self.num)
            while r2 == r1:
                r2 = np.random.randint(self.num)
            left, right = min(r1, r2), max(r1, r2)
            sel = self.child[i, :].copy()
            sel[left:right + 1] = self.child[i, left:right + 1][::-1]
            if self.comp_fit(sel) < self.comp_fit(self.child[i, :]):
                self.child[i, :] = sel
    def Born(self):
        """
        替换，子代变成新的父代
        :return:
        """
        index = np.argsort(self.fitness)[::-1]
        self.parent[index[:self.select_num], :] = self.child
def main(data):
    Path_short = Gena_TSP(data)     # 根据位置坐标，生成一个遗传算法类
    Path_short.rand_parent()        # 初始化父类
    ## 绘制初始化的路径图
    fig, ax = plt.subplots()
    x = data[:, 0]
    y = data[:, 1]
    ax.scatter(x, y, linewidths=0.1)
    for i, txt in enumerate(range(1, len(data) + 1)):
        ax.annotate(txt, (x[i], y[i]))
    res0 = Path_short.parent[0]
    x0 = x[res0]
    y0 = y[res0]
    for i in range(len(data) - 1):
        plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color=&#39;r&#39;, width=0.005, angles=&#39;xy&#39;, scale=1,
                   scale_units=&#39;xy&#39;)
    plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color=&#39;r&#39;, width=0.005, angles=&#39;xy&#39;, scale=1,
               scale_units=&#39;xy&#39;)
    plt.show()
    print(&#39;初始染色体的路程: &#39; + str(Path_short.fitness[0]))
    # 循环迭代遗传过程
    for i in range(Path_short.maxgen):
        Path_short.Select()     # 选择子代
        Path_short.Cross()      # 交叉
        Path_short.Mutation()   # 变异
        Path_short.Reverse()    # 进化逆转
        Path_short.Born()      # 子代插入
        # 重新计算新群体的距离值
        for j in range(Path_short.size_pop):
            Path_short.fitness[j] = Path_short.comp_fit(Path_short.parent[j, :])
        index = Path_short.fitness.argmin()
        if (i + 1) % 50 == 0:
            print(&#39;第&#39; + str(i + 1) + &#39;步后的最短的路程: &#39; + str(Path_short.fitness[index]))
            print(&#39;第&#39; + str(i + 1) + &#39;步后的最优路径:&#39;)
            Path_short.out_path(Path_short.parent[index, :])  # 显示每一步的最优路径
        # 存储每一步的最优路径及距离
        Path_short.best_fit.append(Path_short.fitness[index])
        Path_short.best_path.append(Path_short.parent[index, :])
    return Path_short  # 返回遗传算法结果类
if __name__ == &#39;__main__&#39;:
    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
    main(data)

运行结果

ok,我们来看看运行的结果：

Atas ialah kandungan terperinci Bagaimana untuk menggunakan Python untuk melaksanakan algoritma genetik untuk menyelesaikan Masalah Jurujual Perjalanan (TSP)?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!