Rumah >pembangunan bahagian belakang >Tutorial Python >Kaedah dan langkah untuk melaksanakan simulasi Monte Carlo dalam Python
Kaedah dan langkah untuk melaksanakan simulasi Monte Carlo dalam Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-05-08 11:37:083725semak imbas
Apakah simulasi Monte Carlo
Simulasi Monte Carlo ialah kaedah berdasarkan statistik kebarangkalian, yang menggunakan simulasi rawak untuk mengira kebarangkalian sesuatu peristiwa berlaku. Dalam pengurusan projek, simulasi Monte Carlo digunakan terutamanya untuk mengira taburan kebarangkalian penunjuk utama seperti tempoh projek dan kos, membantu pengurus projek mengurus risiko dan membuat keputusan dengan lebih baik.
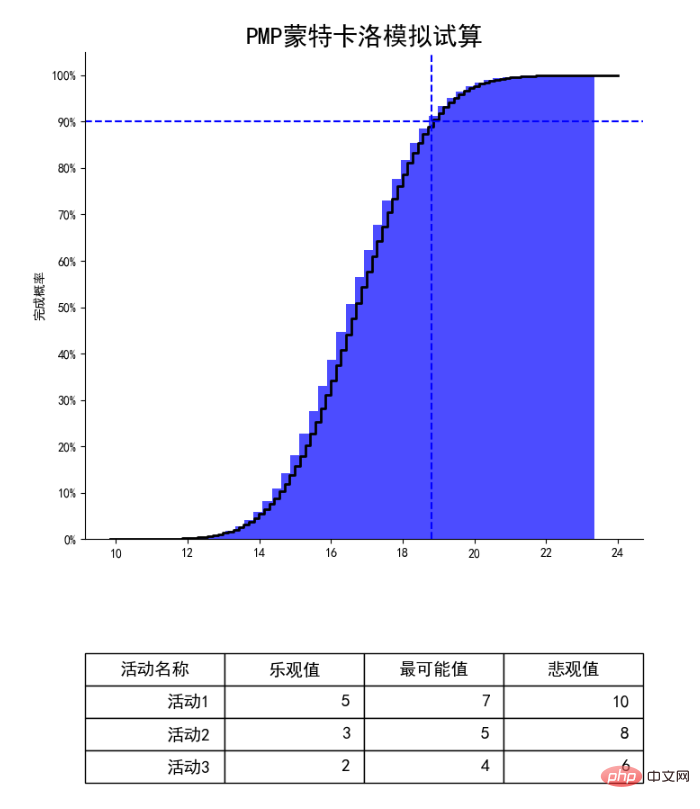
Mari kita lihat gambar di atas Gambar ini adalah simulasi Monte Carlo untuk tiga aktiviti projek: Aktiviti 1, Aktiviti 2 dan Aktiviti 3. Simulasi adalah berdasarkan anggaran tiga mata bagi tiga aktiviti. Kemudian komputer diminta untuk melakukan belanjawan rawak 1,000,000 kali, dan gambar di atas diperolehi.
Mari kita ambil persilangan garis putus-putus biru dalam gambar di atas sebagai contoh. Mari kita lihat paksi-Y 90% di sini merujuk kepada 90% kebarangkalian siap. Paksi mendatar yang sepadan dengan titik ini adalah hampir 19 hari. Dengan kata lain, melalui simulasi komputer 1 juta kali. Kebarangkalian untuk menyiapkan projek dalam masa kurang daripada 19 hari ialah 90%.
Pelajar yang telah membuat projek semua tahu bahawa pelanggan atau pemimpin sentiasa mahu kami pergi lebih cepat, lebih pantas dan lebih pantas. Pemimpin itu berkata bahawa tidak ada 19 hari, hanya 16 hari. Pada masa ini, sebagai pengurus projek, melalui carta di atas, saya mendapati bahawa nilai paksi-X yang sepadan dengan paksi-Y selama 16 hari adalah kira-kira 30%. Tanya sahaja kepada ketua: Kadar kejayaan hanya 30%. Adakah anda mahu bertaruh atau tidak? Kuncinya ialah kesederhanaan, dan teori kebarangkalian untuk menyokong anda.
Pelaksanaan Python
Bagaimana untuk mengira simulasi Monte Carlo pengurusan projek dalam Python? Ia sebenarnya sangat mudah. Kita boleh menggunakan perpustakaan numpy dan matplotlib dalam Python untuk melakukan pengiraan dan lukisan. Cikgu Tian di bawah memberikan kod lengkap:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
"""
#-----------------------------------------------------------------------------
# --- TDOUYA STUDIOS ---
#-----------------------------------------------------------------------------
#
# @Project : di08-tdd-cdg-python-learning
# @File : monte_carlo.py
# @Author : tianxin.xp@gmail.com
# @Date : 2023/3/12 18:22
#
# 用Python实现蒙特卡洛模拟
#
#--------------------------------------------------------------------------"""
from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter, MultipleLocator
from scipy.stats import norm
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def to_percent(y, position):
# 将纵轴用百分数表示
return '{:.0f}%'.format(100 * y)
class Activity:
""" 活动类,用于表示一个项目中的活动
Attributes:
name (str): 活动名称
optimistic (float): 乐观时间
pessimistic (float): 悲观时间
most_likely (float): 最可能时间
"""
def __init__(self, name, optimistic, pessimistic, most_likely):
"""
初始化活动类
Args:
name (str): 活动名称
optimistic (float): 乐观时间
pessimistic (float): 悲观时间
most_likely (float): 最可能时间
"""
self.name = name
self.optimistic = optimistic
self.pessimistic = pessimistic
self.most_likely = most_likely
class PMP:
"""
PMP类用于进行项目管理中的相关计算:
方法:
monte_carlo_simulation : 蒙特卡洛模拟试算,包括计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等功能。
"""
def __init__(self, activities):
"""
初始化PMP类,传入活动列表。
:param activities: 活动列表,包括活动名称、乐观值、最可能值和悲观值。
"""
self.activities = activities
def monte_carlo_simulation(self, n):
"""
进行蒙特卡洛模拟试算,计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等。
:param n: 模拟次数。
"""
# 模拟参数和变量
t = []
for activity in self.activities:
t.append(np.random.triangular(activity.optimistic, activity.most_likely, activity.pessimistic, n))
# 计算项目工期
project_duration = sum(t)
# 计算平均值和标准差
mean_duration = np.mean(project_duration)
std_duration = np.std(project_duration)
# 绘制积累图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 10), gridspec_kw={'height_ratios': [3, 1]})
ax1.hist(project_duration, bins=50, density=True, alpha=0.7, color='blue', cumulative=True)
ax1.yaxis.set_major_locator(MultipleLocator(0.1))
ax1.yaxis.set_major_formatter(FuncFormatter(to_percent))
ax1.set_ylabel('完成概率')
ax1.set_title('PMP蒙特卡洛模拟试算', fontsize=20)
# 绘制概率密度曲线
xmin, xmax = ax1.get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.cdf(x, mean_duration, std_duration)
ax1.plot(x, p, 'k', linewidth=2, drawstyle='steps-post')
# 找到完成概率90%的点
x_90 = norm.ppf(0.9, mean_duration, std_duration)
# 绘制垂线
ax1.axvline(x_90, linestyle='--', color='blue')
ax1.axhline(0.9, linestyle='--', color='blue')
# 隐藏右边和上方的坐标轴线
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
# 添加表格
col_labels = ['活动名称', '乐观值', '最可能值', '悲观值']
cell_text = [[activity.name, activity.optimistic, activity.most_likely, activity.pessimistic] for activity in
self.activities]
table = ax2.table(cellText=cell_text, colLabels=col_labels, loc='center')
# 设置表格的字体大小和行高
table.auto_set_font_size(False)
table.set_fontsize(14)
# # 设置表格的行高为1.5倍原来的高度
for i in range(len(self.activities) + 1):
table._cells[(i, 0)].set_height(0.2)
table._cells[(i, 1)].set_height(0.2)
table._cells[(i, 2)].set_height(0.2)
table._cells[(i, 3)].set_height(0.2)
ax2.axis('off')
# 调整子图之间的间距和边距
plt.subplots_adjust(hspace=0.3, bottom=0.05)
# 保存图表
now = datetime.now().strftime('%Y%m%d%H%M%S')
plt.savefig('monte_carlo_simulation_{}.png'.format(now))
# 显示图形
plt.show()
if __name__ == '__main__':
# 模拟参数和变量
n = 1000000 # 模拟次数
# 活动的工期分布
activities = [
Activity('活动1', 5, 10, 7),
Activity('活动2', 3, 8, 5),
Activity('活动3', 2, 6, 4)
]
# 进行蒙特卡洛模拟
pmp = PMP(activities)
pmp.monte_carlo_simulation(n)Atas ialah kandungan terperinci Kaedah dan langkah untuk melaksanakan simulasi Monte Carlo dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

