Bagaimana untuk menggunakan Python untuk melaksanakan algoritma PSO untuk menyelesaikan masalah TSP?

Algoritma PSO

Jadi sebelum kita mula, mari kita bincangkan tentang algoritma PSO asas. Intinya hanyalah satu:

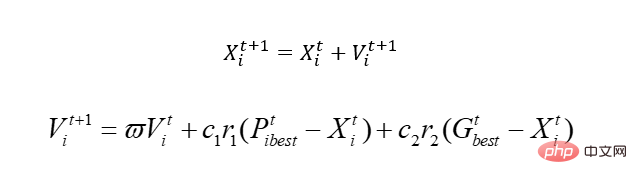
Biar kami terangkan formula ini dan anda akan faham.

Peraturan lama ialah kita menganggap terdapat persamaan y=sin(x1)+cos(x2)

Algoritma PSO mencapai pengoptimuman kami dengan mensimulasikan migrasi burung ? Setelah berkata demikian, mari kita bercakap tentang teras ini.

Dalam persamaan yang baru kita ada, terdapat dua pembolehubah, x1, x2. Kerana ia adalah burung simulasi, untuk merealisasikan kaedah buta, konsep kelajuan diperkenalkan di sini, dan x secara semula jadi adalah domain yang boleh dilaksanakan kami, iaitu ruang penyelesaian. Dengan menukar kelajuan, x digerakkan, iaitu nilai x diubah. Antaranya, Pbest mewakili penyelesaian optimum dalam kedudukan di mana burung telah berjalan, dan Gbest mewakili penyelesaian optimum bagi seluruh populasi. Apa yang anda maksudkan, iaitu, apabila ia bergerak, burung ini mungkin bergerak ke kedudukan yang lebih teruk, kerana tidak seperti genetik, ia akan dibunuh jika ia buruk, tetapi yang ini tidak. Sudah tentu, terdapat banyak isu tempatan yang terlibat, yang tidak akan kami bincangkan di sini Tiada algoritma yang sempurna, dan yang ini betul.

Proses algoritma

Proses utama algoritma:

Langkah pertama: Mulakan kedudukan rawak dan kelajuan kawanan zarah, dan tetapkan bilangan lelaran.

Langkah 2: Kira nilai kecergasan setiap zarah.

Langkah 3: Bagi setiap zarah, bandingkan nilai kecergasannya dengan nilai kesesuaian kedudukan terbaik yang saya alami. Jika lebih baik, gunakannya sebagai kedudukan optimum individu semasa.

Langkah 4: Untuk setiap zarah, bandingkan nilai kecergasannya dengan nilai kecergasan kedudukan terbaik global yang dialami jika ia lebih baik, gunakan ia sebagai kedudukan optimum global semasa.

Langkah 5: Optimumkan kelajuan dan kedudukan zarah mengikut formula kelajuan dan kedudukan untuk mengemas kini kedudukan zarah.

Langkah 6: Jika syarat akhir tidak dipenuhi (biasanya bilangan maksimum kitaran atau keperluan ralat minimum), kembali ke langkah kedua

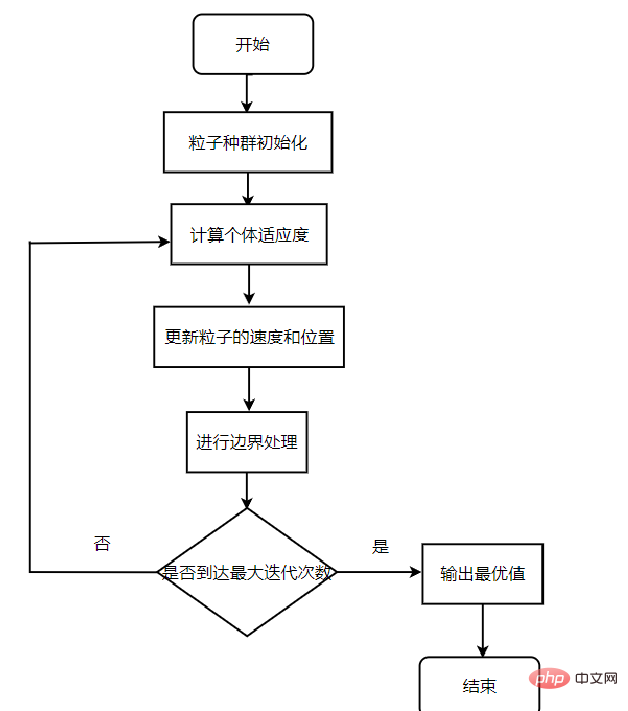
Kelebihan:

Algoritma PSO tidak mempunyai operasi silang dan mutasi, dan bergantung pada kelajuan zarah untuk melengkapkan carian Dalam evolusi berulang, hanya zarah optimum menghantar maklumat kepada zarah lain, dan kelajuan carian adalah pantas .

Algoritma PSO mempunyai ingatan, dan kedudukan terbaik sejarah kumpulan zarah boleh dihafal dan dihantar ke zarah lain.

Terdapat lebih sedikit parameter yang perlu dilaraskan, strukturnya ringkas dan mudah dilaksanakan dalam kejuruteraan.

Menggunakan pengekodan nombor sebenar, yang ditentukan secara langsung oleh penyelesaian masalah Bilangan pembolehubah dalam penyelesaian masalah digunakan secara langsung sebagai dimensi zarah.

Kelemahan:

Kekurangan pelarasan dinamik kelajuan dan mudah jatuh ke dalam optimum tempatan, mengakibatkan ketepatan penumpuan yang rendah dan kesukaran dalam penumpuan.

Tidak dapat menyelesaikan masalah pengoptimuman diskret dan kombinatorial dengan berkesan.

Kawalan parameter, untuk masalah yang berbeza, cara memilih parameter yang sesuai untuk mencapai hasil yang optimum.

tidak dapat menyelesaikan beberapa masalah penerangan sistem koordinat bukan kartesian dengan berkesan,

pelaksanaan mudah

ok, mari kita lihat pelaksanaan paling mudah:

import numpy as np
import random
class PSO_model:
    def __init__(self,w,c1,c2,r1,r2,N,D,M):
        self.w = w # 惯性权值
        self.c1=c1
        self.c2=c2
        self.r1=r1
        self.r2=r2
        self.N=N # 初始化种群数量个数
        self.D=D # 搜索空间维度
        self.M=M # 迭代的最大次数
        self.x=np.zeros((self.N,self.D))  #粒子的初始位置
        self.v=np.zeros((self.N,self.D))  #粒子的初始速度
        self.pbest=np.zeros((self.N,self.D))  #个体最优值初始化
        self.gbest=np.zeros((1,self.D))  #种群最优值
        self.p_fit=np.zeros(self.N)
        self.fit=1e8 #初始化全局最优适应度
# 目标函数，也是适应度函数（求最小化问题）
    def function(self,x):
        A = 10
        x1=x[0]
        x2=x[1]
        Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
        return Z
     # 初始化种群
    def init_pop(self):
        for i in range(self.N):
            for j in range(self.D):
                self.x[i][j] = random.random()
                self.v[i][j] = random.random()
            self.pbest[i] = self.x[i] # 初始化个体的最优值
            aim=self.function(self.x[i]) # 计算个体的适应度值
            self.p_fit[i]=aim # 初始化个体的最优位置
            if aim < self.fit:  # 对个体适应度进行比较，计算出最优的种群适应度
                self.fit = aim
                self.gbest = self.x[i]
    # 更新粒子的位置与速度
    def update(self):
        for t in range(self.M): # 在迭代次数M内进行循环
            for i in range(self.N): # 对所有种群进行一次循环
                aim=self.function(self.x[i]) # 计算一次目标函数的适应度
                if aim<self.p_fit[i]: # 比较适应度大小，将小的负值给个体最优
                    self.p_fit[i]=aim
                    self.pbest[i]=self.x[i]
                    if self.p_fit[i]<self.fit: # 如果是个体最优再将和全体最优进行对比
                        self.gbest=self.x[i]
                        self.fit = self.p_fit[i]
            for i in range(self.N): # 更新粒子的速度和位置
                self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
                self.x[i]=self.x[i]+self.v[i]
        print("最优值：",self.fit,"位置为：",self.gbest)
if __name__ == &#39;__main__&#39;:
    # w,c1,c2,r1,r2,N,D,M参数初始化
    w=random.random()
    c1=c2=2#一般设置为2
    r1=0.7
    r2=0.5
    N=30
    D=2
    M=200
    pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#设置初始权值
    pso_object.init_pop()
    pso_object.update()

TSP yang diselesaikan

Perwakilan Data

Pertama sekali, menggunakan PSO sebenarnya serupa dengan penggunaan genetik kami sebelum ini. Kami masih menggunakan matriks untuk mewakili populasi, dan matriks untuk mewakili jarak antara bandar-bandar.

      # 群体的初始化和路径的初始化
        self.population = np.array([0] * self.num_pop * self.num).reshape(
            self.num_pop, self.num)
        self.fitness = [0] * self.num_pop
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()

Perbezaan

Apakah perbezaan terbesar antara ia dengan PSO asal kami Ia sebenarnya mudah dan pantas, dan ia berkaitan dengan kelajuan kami mengemas kini. Apabila kita berhadapan dengan masalah berterusan, ia sebenarnya seperti ini:

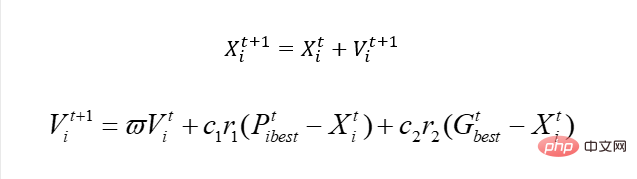
Begitu juga, kita boleh menggunakan X untuk mewakili nombor bandar, tetapi jelas kita tidak boleh menggunakan penyelesaian ini untuk mengemas kini kelajuan.

Pada masa ini, apabila kita mengemas kini kelajuan, kita perlu menggunakan penyelesaian baru Jadi penyelesaian ini sebenarnya kemas kini X menggunakan algoritma genetik. Secara terang-terangan, sebab mengapa kita memerlukan kelajuan adalah untuk mengemas kini X dan membuat X bergerak ke arah yang baik. Kini tidak lagi boleh menggunakan kemas kini kelajuan, jadi kami mengemas kini X pula, jadi mengapa tidak pilih sahaja penyelesaian yang boleh mengemas kini X ini dengan baik? Oleh itu, genetik boleh digunakan secara langsung di sini, kemas kini kelajuan kami adalah berdasarkan Pbest dan Gbest, dan kemudian "dipelajari" mengikut berat tertentu Dengan cara ini, V ini mempunyai "ciri" Pbest dan Gbest. Jadi jika itu yang berlaku, maka apabila saya secara langsung meniru silang genetik dan menyeberanginya dengan Best, tidakkah saya boleh mempelajari beberapa "ciri" yang sepadan?

    def cross_1(self, path, best_path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        cross = best_path[left:right + 1]
        for i in range(right - left + 1):
            for k in range(self.num):
                if path[k] == cross[i]:
                    path[k:self.num - 1] = path[k + 1:self.num]
                    path[-1] = 0
        path[self.num - right + left - 1:self.num] = cross
        return path

Pada masa yang sama kita masih boleh memperkenalkan mutasi.

    def mutation(self,path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        path[r1],path[r2] = path[r2],path[r1]
        return path

Kod penuh

ok, sekarang mari lihat kod lengkap:

import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
    def __init__(self ,data ,num_pop=200):
        self.num_pop = num_pop  # 群体个数
        self.data = data        # 城市坐标
        self.num =len(data)     # 城市个数
        # 群体的初始化和路径的初始化
        self.population = np.array([0] * self.num_pop * self.num).reshape(
            self.num_pop, self.num)
        self.fitness = [0] * self.num_pop
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()
    def __matrix_dis(self):
        """
        计算14个城市的距离，将这些距离用矩阵存起来
        :return:
        """
        res = np.zeros((self.num, self.num))
        for i in range(self.num):
            for j in range(i + 1, self.num):
                res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
                res[j, i] = res[i, j]
        return res
    def cross_1(self, path, best_path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        cross = best_path[left:right + 1]
        for i in range(right - left + 1):
            for k in range(self.num):
                if path[k] == cross[i]:
                    path[k:self.num - 1] = path[k + 1:self.num]
                    path[-1] = 0
        path[self.num - right + left - 1:self.num] = cross
        return path
    def mutation(self,path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        path[r1],path[r2] = path[r2],path[r1]
        return path
    def comp_fit(self, one_path):
        """
        计算，咱们这个路径的长度，例如A-B-C-D
        :param one_path:
        :return:
        """
        res = 0
        for i in range(self.num - 1):
            res += self.__matrix_distance[one_path[i], one_path[i + 1]]
        res += self.__matrix_distance[one_path[-1], one_path[0]]
        return res
    def out_path(self, one_path):
        """
        输出我们的路径顺序
        :param one_path:
        :return:
        """
        res = str(one_path[0] + 1) + '-->'
        for i in range(1, self.num):
            res += str(one_path[i] + 1) + '-->'
        res += str(one_path[0] + 1) + '\n'
        print(res)
    def init_population(self):
        """
        初始化种群
        :return:
        """
        rand_ch = np.array(range(self.num))
        for i in range(self.num_pop):
            np.random.shuffle(rand_ch)
            self.population[i, :] = rand_ch
            self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
    Path_short = HybridPsoTSP(data, num_pop=num_pop)  # 混合粒子群算法类
    Path_short.init_population()  # 初始化种群
    # 初始化路径绘图
    fig, ax = plt.subplots()
    x = data[:, 0]
    y = data[:, 1]
    ax.scatter(x, y, linewidths=0.1)
    for i, txt in enumerate(range(1, len(data) + 1)):
        ax.annotate(txt, (x[i], y[i]))
    res0 = Path_short.population[0]
    x0 = x[res0]
    y0 = y[res0]
    for i in range(len(data) - 1):
        plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
                   scale_units='xy')
    plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
               scale_units='xy')
    plt.show()
    print('初始染色体的路程: ' + str(Path_short.fitness[0]))
    # 存储个体极值的路径和距离
    best_P_population = Path_short.population.copy()
    best_P_fit = Path_short.fitness.copy()
    min_index = np.argmin(Path_short.fitness)
    # 存储当前种群极值的路径和距离
    best_G_population = Path_short.population[min_index, :]
    best_G_fit = Path_short.fitness[min_index]
    # 存储每一步迭代后的最优路径和距离
    best_population = [best_G_population]
    best_fit = [best_G_fit]
    # 复制当前群体进行交叉变异
    x_new = Path_short.population.copy()
    for i in range(max_n):
        # 更新当前的个体极值
        for j in range(num_pop):
            if Path_short.fitness[j] < best_P_fit[j]:
                best_P_fit[j] = Path_short.fitness[j]
                best_P_population[j, :] = Path_short.population[j, :]
        # 更新当前种群的群体极值
        min_index = np.argmin(Path_short.fitness)
        best_G_population = Path_short.population[min_index, :]
        best_G_fit = Path_short.fitness[min_index]
        # 更新每一步迭代后的全局最优路径和解
        if best_G_fit < best_fit[-1]:
            best_fit.append(best_G_fit)
            best_population.append(best_G_population)
        else:
            best_fit.append(best_fit[-1])
            best_population.append(best_population[-1])
        # 将每个个体与个体极值和当前的群体极值进行交叉
        for j in range(num_pop):
            # 与个体极值交叉
            x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
            fit = Path_short.comp_fit(x_new[j, :])
            # 判断是否保留
            if fit < Path_short.fitness[j]:
                Path_short.population[j, :] = x_new[j, :]
                Path_short.fitness[j] = fit
            # 与当前极值交叉
            x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
            fit = Path_short.comp_fit(x_new[j, :])
            if fit < Path_short.fitness[j]:
                Path_short.population[j, :] = x_new[j, :]
                Path_short.fitness[j] = fit
            # 变异
            x_new[j, :] = Path_short.mutation(x_new[j, :])
            fit = Path_short.comp_fit(x_new[j, :])
            if fit <= Path_short.fitness[j]:
                Path_short.population[j] = x_new[j, :]
                Path_short.fitness[j] = fit
        if (i + 1) % 20 == 0:
            print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
            print('第' + str(i + 1) + '步后的最优路径:')
            Path_short.out_path(Path_short.population[min_index, :])  # 显示每一步的最优路径
    Path_short.best_population = best_population
    Path_short.best_fit = best_fit
    return Path_short  # 返回结果类
if __name__ == '__main__':
    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
    main(data)

初始染色体的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9

可以看到收敛速度还是很快的。

特点分析

ok,到目前为止的话，我们介绍了两个算法去解决TSP或者是优化问题。我们来分析一下，这些算法有什么特点，为啥可以达到我们需要的优化效果。其实不管是遗传还是PSO，你其实都可以发现，有一个东西，我们可以暂且叫它环境压力。我们通过物竞天择，或者鸟类迁移，进行模拟寻优。而之所以需要这样做，是因为我们指定了一个规则，在我们的规则之下。我们让模拟的种群有一种压力去靠拢，其中物竞天择和鸟类迁移只是我们的一种手段，去应对这样的“压力”。所以的对于这种算法而言，最核心的点就两个：

设计环境压力

我们需要做优化问题，所以我们必须要能够让我们的解往那个方向走，需要一个驱动，需要一个压力。因此我们需要设计这样的一个环境，在遗传算法，粒子群算法是通过种群当中的生存，来进行设计的它的压力是我们的目标函数。由种群和目标函数（目标指标）构成了一个环境和压力。

设计压力策略

之后的话，我们设计好了一个环境和压力，那么未来应对这种压力，我们需要去设计一种策略，来应付这种压力。遗传算法是通过PUA自己，也就是种群的优胜略汰。PSO是通过学习，学习种群的优秀粒子和过去自己家的优秀“祖先”来应对这种压力的。

强化学习

所以的话，我们是否可以使用别的方案来实现这种优化效果。，在强化学习的算法框架里面的话，我们明确的知道了为什么他们可以实现优化，是环境压力+压力策略。恰好咱们强化学习是有环境的，适应函数和环境恰好可以组成环境+压力。本身的算法收敛过程就是我们的压力策略。所以我们完全是可以直接使用强化学习进行这个处理的。那么在这里咱们就来使用强化学习在下一篇文章当中。

Atas ialah kandungan terperinci Bagaimana untuk menggunakan Python untuk melaksanakan algoritma PSO untuk menyelesaikan masalah TSP?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!