Rumah >pembangunan bahagian belakang >Tutorial Python >Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS)
Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS)
- PHPzke hadapan
- 2023-04-30 12:22:061630semak imbas
POCS: Unjuran ke Set Cembung. Dalam matematik, set cembung ialah set di mana mana-mana ruas garis antara mana-mana dua titik berada dalam set. Unjuran ialah operasi memetakan titik ke subruang dalam ruang lain. Memandangkan set cembung dan titik, anda boleh beroperasi dengan mencari unjuran titik ke set cembung. Unjuran ialah titik dalam set cembung yang paling hampir dengan titik dan boleh dikira dengan meminimumkan jarak antara titik ini dan mana-mana titik lain dalam set cembung. Memandangkan ia adalah unjuran, kita boleh memetakan ciri kepada set cembung dalam ruang lain, supaya operasi seperti pengelompokan atau pengurangan dimensi boleh dilakukan.
Artikel ini menyemak algoritma pengelompokan berdasarkan kaedah unjuran set cembung, iaitu algoritma pengelompokan berdasarkan POCS. Kertas asal diterbitkan di IWIS2022.
Set cembung
Set cembung ditakrifkan sebagai satu set titik data, di mana segmen garisan yang menghubungkan mana-mana dua titik x1 dan x2 dalam set disertakan sepenuhnya dalam set ini. Mengikut definisi set cembung, set kosong ∅, set unitari, segmen garis, hyperplane, dan sfera Euclidean semuanya dianggap sebagai set cembung. Titik data juga dianggap sebagai set cembung kerana ia adalah set tunggal (set dengan hanya satu elemen). Ini membuka laluan baharu untuk menggunakan konsep POCS pada titik data berkelompok.
Projection of Convex Sets (POCS)
Kaedah POCS secara kasar boleh dibahagikan kepada dua jenis: berselang-seli dan selari.
1. Poc berselang seli
Bermula dari mana-mana titik dalam ruang data, unjuran berselang-seli dari titik ini kepada dua (atau lebih) set cembung bersilang akan menumpu ke titik persilangan yang ditetapkan Satu titik, contohnya rajah berikut:
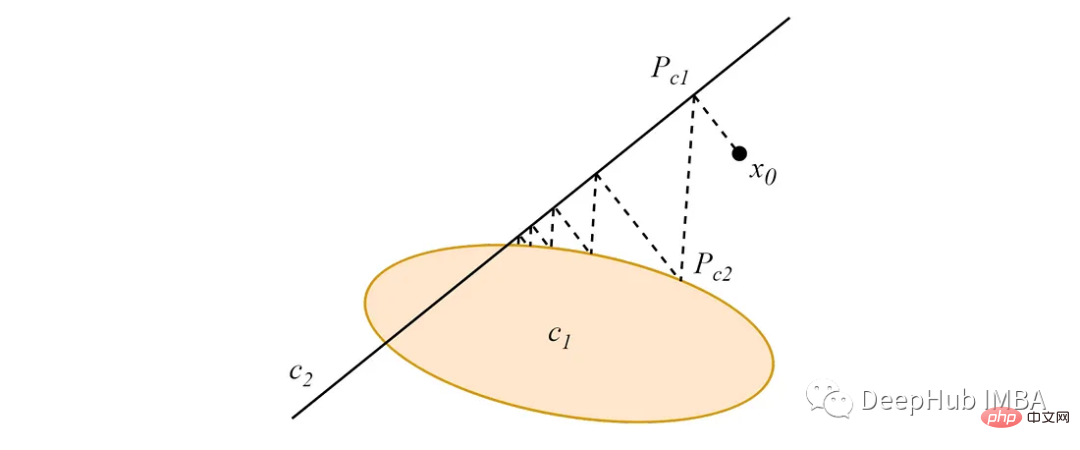
Apabila set cembung tidak bersilang, unjuran berselang-seli akan menumpu kepada kitaran had tamak yang bergantung pada susunan unjuran.
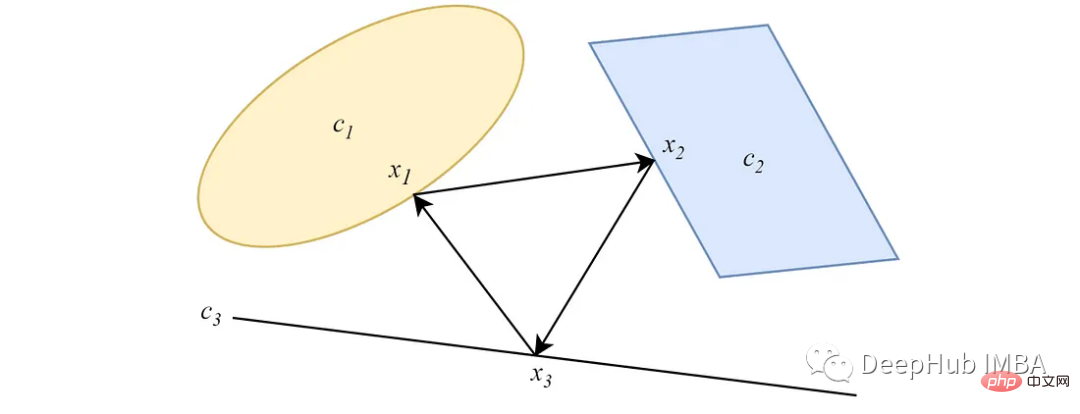
2. POCS Selari
Berbeza daripada bentuk berselang-seli, projek POCS selari dari titik data ke semua set cembung secara serentak, dan setiap unjuran Semua mempunyai kepentingan berat badan. Untuk dua set cembung bersilang yang tidak kosong, serupa dengan versi berselang-seli, unjuran selari menumpu ke satu titik di persimpangan set.
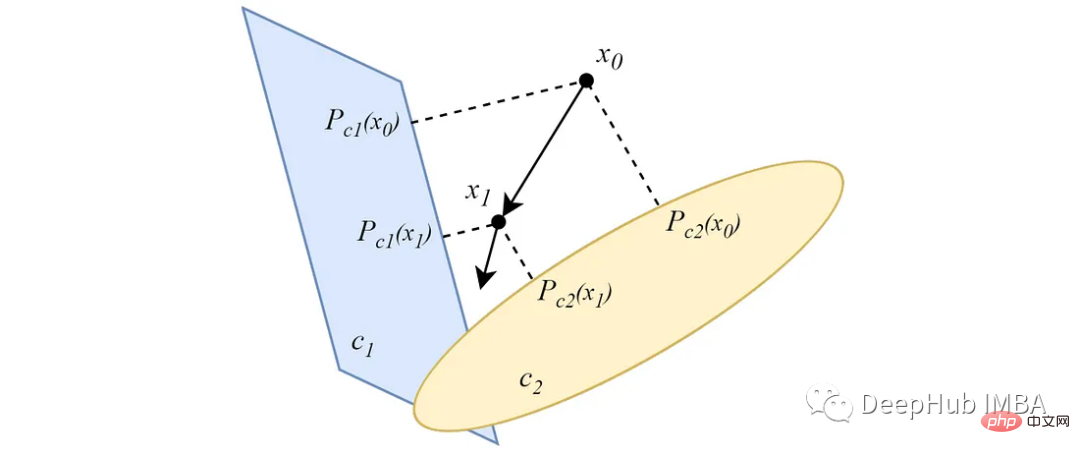
Dalam kes di mana set cembung tidak bersilang, unjuran akan menumpu kepada penyelesaian minimum. Idea utama algoritma pengelompokan berasaskan POC datang daripada ciri ini.
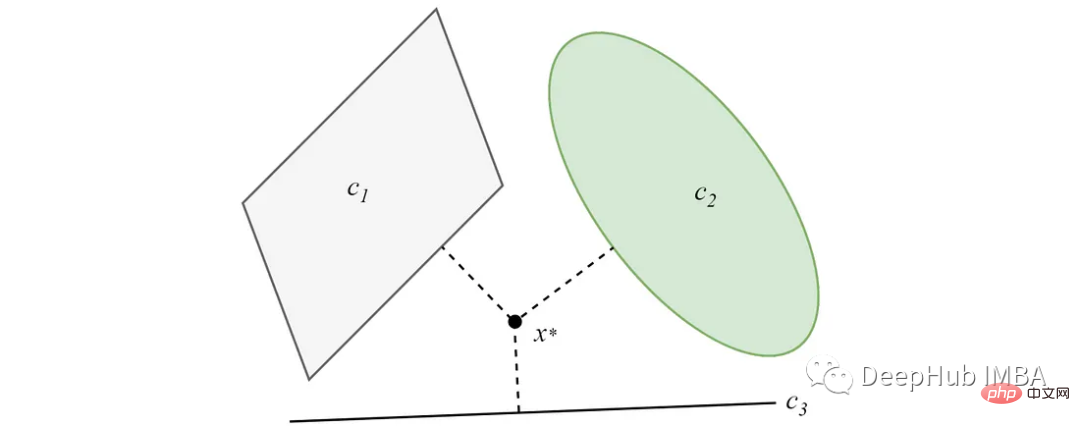
Untuk butiran lanjut tentang POCS, anda boleh melihat kertas asal
Algoritma pengelompokan berasaskan POCS
Menggunakan penumpuan selari Harta kaedah POCS, pengarang kertas itu mencadangkan algoritma pengelompokan yang sangat mudah tetapi berkesan pada tahap tertentu. Algoritma ini berfungsi sama dengan algoritma K-Means klasik, tetapi terdapat perbezaan dalam cara setiap titik data diproses: algoritma K-Means menimbang kepentingan setiap titik data yang sama, tetapi algoritma pengelompokan berasaskan POC Setiap titik data ditimbang secara berbeza dalam kepentingan, yang berkadar dengan jarak titik data daripada prototaip kelompok.
Pseudokod algoritma adalah seperti berikut:

Hasil eksperimen
Pengarang menguji algoritma berasaskan POC pada beberapa penanda aras awam set data Prestasi algoritma pengelompokan. Jadual di bawah meringkaskan perihalan set data ini.
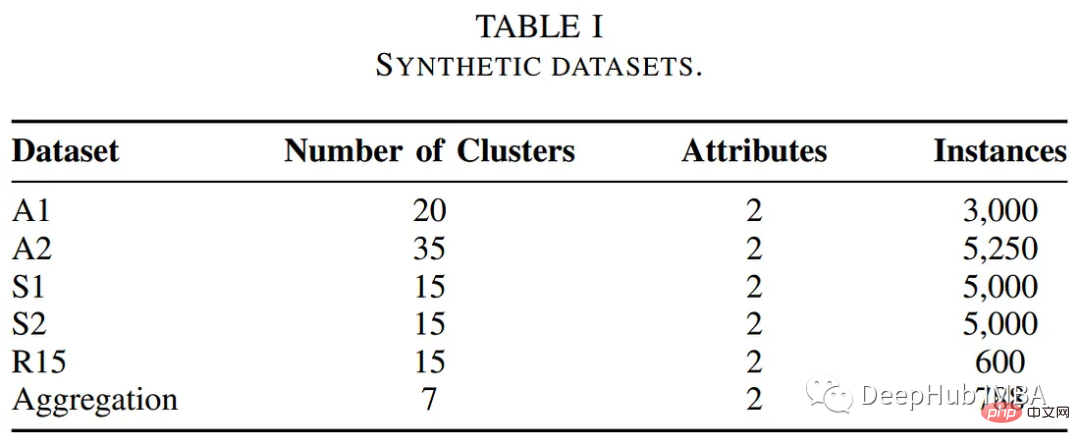
Pengarang membandingkan prestasi algoritma pengelompokan berasaskan POC dengan kaedah pengelompokan tradisional lain, termasuk algoritma k-means dan fuzzy c-means. Jadual berikut meringkaskan penilaian dari segi masa pelaksanaan dan ralat pengelompokan.
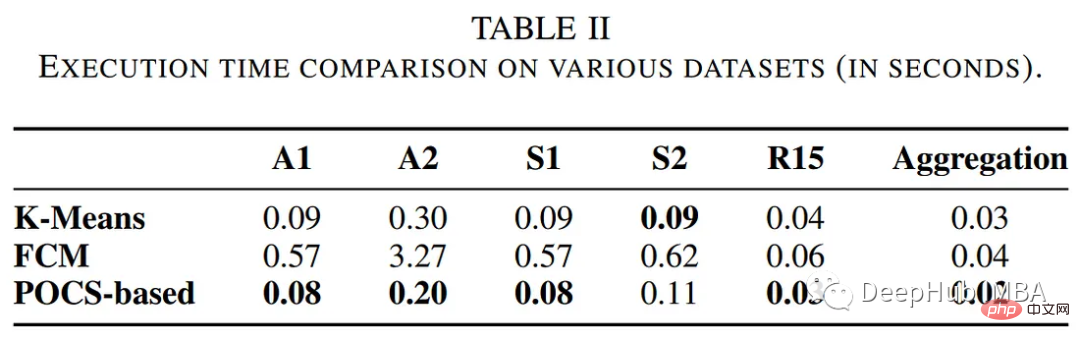
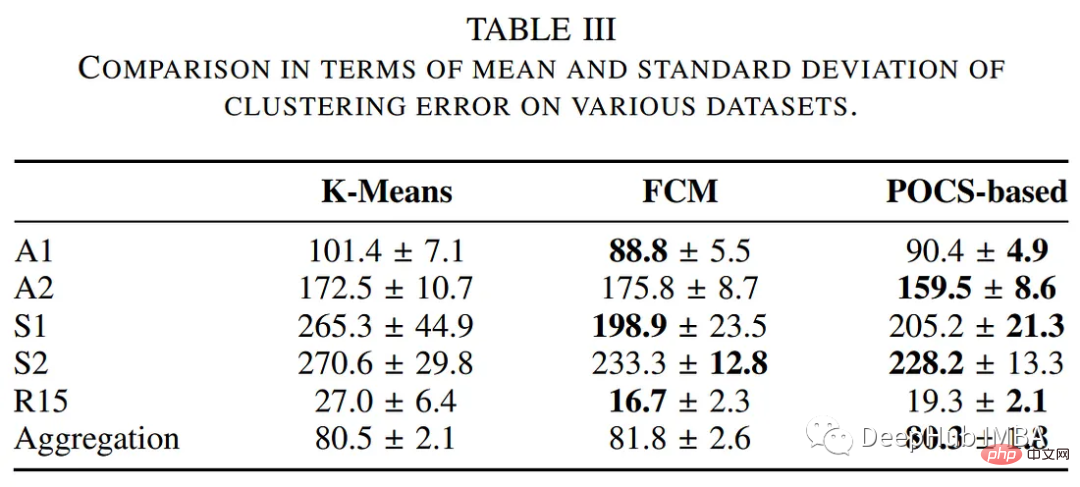
Hasil pengelompokan ditunjukkan di bawah:

Kod sampel
Kami menggunakan algoritma ini pada set data yang sangat mudah. Pengarang telah mengeluarkan pakej untuk kegunaan langsung, yang boleh kita gunakan terus untuk aplikasi:
pip install pocs-based-clustering
Buat set data ringkas 5000 titik data berpusat pada 10 gugusan:
# Import packages import time import matplotlib.pyplot as plt from sklearn.datasets import make_blobs from pocs_based_clustering.tools import clustering # Generate a simple dataset num_clusters = 10 X, y = make_blobs(n_samples=5000, centers=num_clusters, cluster_std=0.5, random_state=0) plt.figure(figsize=(8,8)) plt.scatter(X[:, 0], X[:, 1], s=50) plt.show()

Lakukan pengelompokan dan paparkan hasilnya:
# POSC-based Clustering Algorithm centroids, labels = clustering(X, num_clusters, 100) # Display results plt.figure(figsize=(8,8)) plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis') plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red') plt.show()

总结
我们简要回顾了一种简单而有效的基于投影到凸集(POCS)方法的聚类技术,称为基于POCS的聚类算法。该算法利用POCS的收敛特性应用于聚类任务,并在一定程度上实现了可行的改进。在一些基准数据集上验证了该算法的有效性。
论文的地址如下:https://arxiv.org/abs/2208.08888
作者发布的源代码在这里:https://github.com/tranleanh/pocs-based-clustering
Atas ialah kandungan terperinci Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

