Rumah >Java >javaTutorial >Apakah teknik untuk operasi bit java?
Apakah teknik untuk operasi bit java?
- PHPzke hadapan
- 2023-04-29 10:34:061633semak imbas
Apakah itu operasi bit
Kita semua tahu bahawa bentuk data yang disimpan dalam komputer ialah data binari operasi bit adalah kaedah pengendalian data pada peringkat binari. Operasi bit Secara langsung beroperasi pada data binari yang terdiri daripada 0 dan 1.
Operasi bit asas
Terdapat enam operasi bit asas, iaitu** DAN atau TIDAK XOR anjakan kiri anjakan kanan**
| 符号 | 描述 | 运算规则 |
|---|---|---|
| & | 与 | 两个位都为1时,结果才为1 |
| 或 | 两个位都为0时,结果才为0 | |
| ^ | 异或 | 两个位相同时,结果为1,不相同为0 |
| ~ | 取反 | 0变1,1变0 |
| 左移 | 各二进位全部左移若干位,高位丢弃,低位补0 | |
| >> | 右移 | 各二进位全部左移若干位,高位丢弃,高位补符号位,或者补零,根据不同编译器 |
** Pertama sekali, mesti jelas bahawa operasi bit hanya boleh beroperasi pada integer**
Dalam jdk, java right shift ialah aritmetik operasi anjakan kanan
** Operasi bitwise mempunyai keutamaan yang sangat rendah, jadi sebaiknya gunakan kurungan**
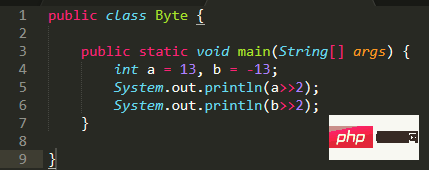
Hasil keluaran kod di atas:
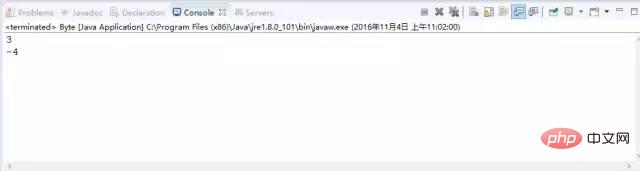
Mari kita analisa mengapa keputusan ini dikeluarkan:
Pertama daripada semua, untuk 13 , kami menulis perduaannya: 0000 1101
anjakan ke kanan dengan dua tempat: 0000 0011. Memandangkan anjakan kanan dalam jdk ialah anjakan kanan aritmetik, bit tinggi ialah diisi dengan 00, dan hasilnya ialah 3
Untuk -13, kod binari: 1111 0011
Anjak ke kanan sebanyak dua bit, tinggi- bit tanda pelengkap pesanan, 1111 1100, hasilnya ialah -4
Teknik yang biasa digunakan untuk operasi bit
Bit operasi sering digunakan untuk operasi kecil kerana ia hanya boleh beroperasi pada nombor bulat, jadi penggunaannya adalah terhad, tetapi beberapa petua yang biasa digunakan patut dikuasai, seperti menilai ganjil dan genap, menukar dua nombor, bertukar tanda, mencari nilai mutlak, dll. Kami akan memperkenalkan mereka satu persatu di bawah.
Pariti Hakim
Perbezaan antara pariti dan kesamarataan dicerminkan dalam binari, iaitu, penghujungnya ialah 0, 1. Jelas sekali, apabila penghujungnya 0, ia ialah nombor genap, dan apabila penghujungnya ialah 1, ia adalah nombor ganjil Satu yang terakhir. Jadi cara untuk menentukan pariti ialah:
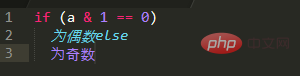
Atur cara ujian kecil:
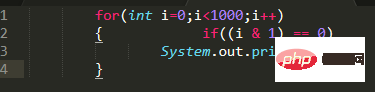
Program di atas akan mengeluarkan semua Even nombor dalam lingkungan 1000
Menukar dua nombor
Kelebihan menggunakan operasi bit untuk menukar dua nombor ialah tidak perlu pembolehubah temp ketiga (hadnya ialah hanya pembolehubah integer boleh ditukar)

Analisis bagaimana pertukaran berlaku:
Pertama a^=b, iaitu, a=(a^b);
b^=a, iaitu b= b(ab), kerana operasi memenuhi undang-undang komutatif, b(ab)=b b^a. Nombor yang di-XOR dengan dirinya mestilah 0, kerana ia mesti sama dengan dirinya Jadi jika nombor di-XOR dengan 0, 1 dan 0 akan tetap 1, dan 0 dan 0 akan tetap 0, jadi jelas nombor dan. 0 Selepas XOR, sudah tentu ia masih sendiri. Jadi pada masa ini, b diberikan nilai a.
Langkah terakhir, a^=b ialah a=ab Memandangkan dua langkah sebelumnya menunjukkan bahawa a=(ab), b=a, jadi a=ab ialah. a=( ab)^a. Oleh itu, a akan diberikan nilai b.
Menukar tanda
Menukar tanda jelas sangat mudah Menurut kod pelengkap yang serupa, cuma ambil songsang dan tambah satu.

Mencari nilai mutlak
Mencari nilai mutlak dicapai berdasarkan perubahan tanda tentukan sama ada ia adalah nombor negatif, jika ia adalah nombor negatif, tukar tanda itu, jika tidak, kembalikan terus.
Untuk menentukan positif atau negatif, anda boleh terus tentukan bit tanda, alihkan 31 bit ke kanan, dapatkan bit tanda, dan tentukan positif atau negatif
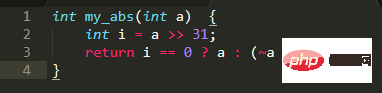
Untuk sebarang nombor, XOR dengan 0 akan Kekal tidak berubah, XOR dengan -1, iaitu 0xFFFFFFFF, adalah bersamaan dengan penolakan. Oleh itu, nilai mutlak juga boleh diperolehi dengan XORing a dengan i dan kemudian tolak i (kerana i ialah 0 atau -1, jadi tolak i bermakna sama ada menambah 0 atau menambah 1). Oleh itu, kod di atas boleh dioptimumkan:
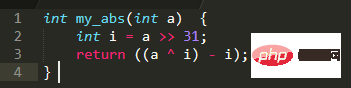
Aplikasi operasi bit
Masalah algoritma biasa, pelaksanaan bit operasi Operasi A+B ialah masalah algoritma biasa.
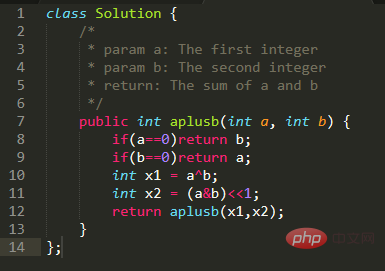
Kod di atas merealisasikan penambahan dua nombor menggunakan operasi bit tanpa menggunakan operator +.
Sekarang mari kita terangkan prinsip operasi bit untuk menambah dua nombor
Pertama sekali, dalam sistem perpuluhan, kita tahu bahawa, 7+8, jumlah tanpa bawa ialah 5, dan bawa ialah 1, maka kita boleh jumlah mengikut jumlah tanpa bawa Bawa 5+1*10 untuk mengira keputusan akhir 15.
Kaedah ini juga boleh diguna pakai untuk sistem binari
Contohnya
a = 3, b = 6
a : 0011
b : 0110
Jumlah tanpa bawa: 0101 iaitu 5
Bawa: 0010 iaitu 2
Jadi a+b menjadi 5 + (25 0101
2Tiada bawa dan 0001 = 1
Bawa 0100 = 4
Jadi a + b menjadi 1 + 4 Kemudian ada
1 0001
4 tanpa bawa dan 10 9
Bawa 0000 = 0
Apabila pembawa ialah 0, jumlah tanpa bawa ialah 9, iaitu jumlah a + b.
Anda boleh mendapati bahawa perkara di atas adalah proses rekursif, jadi tidak sukar untuk menulis kod. Mencari jumlah bebas bawa bagi dua nombor sebenarnya hanyalah operasi XOR bagi dua nombor itu.
Atas ialah kandungan terperinci Apakah teknik untuk operasi bit java?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

