Apakah kaedah pelaksanaan algoritma KMP di Jawa?

Ilustrasi

Algoritma kmp mempunyai persamaan tertentu dengan idea algoritma bm yang dinyatakan sebelum ini. Seperti yang dinyatakan sebelum ini, terdapat konsep akhiran yang baik dalam algoritma bm, dan terdapat konsep awalan yang baik dalam kmp Apakah awalan yang baik Mari kita lihat contoh berikut.

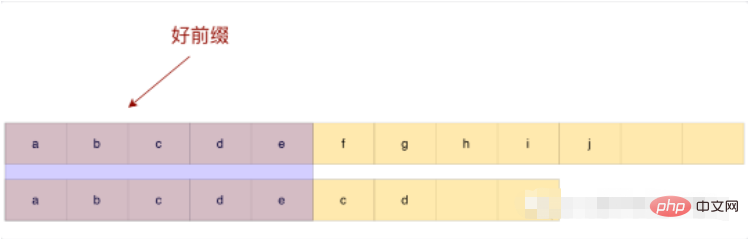
Perhatikan contoh di atas, abcde yang telah dipadankan dipanggil awalan yang baik, a tidak sepadan dengan bcde berikut, jadi tidak perlu membandingkan lagi, slaid terus selepas e Itu sahaja.

Bagaimana jika terdapat aksara yang sepadan dalam awalan yang baik?

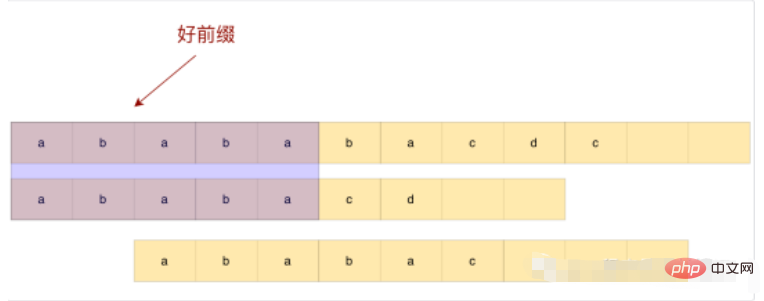
Perhatikan contoh di atas Jika kita meluncur terus selepas awalan, kita akan meluncur terlalu banyak dan terlepas subrentetan yang sepadan. Jadi bagaimana kita melakukan gelongsor yang munasabah berdasarkan awalan yang baik?

Malah, ia adalah untuk menyemak sama ada awalan dan akhiran awalan baik semasa padan, mencari panjang padanan terpanjang dan slaid terus. Memandangkan untuk mencari panjang padanan terpanjang lebih daripada sekali, kami boleh memulakan tatasusunan dahulu dan menyimpan panjang padanan terpanjang di bawah awalan yang baik semasa pada masa ini, tatasusunan kami yang seterusnya akan keluar.

Kami menentukan tatasusunan seterusnya, yang mewakili panjang subrentetan padanan terpanjang bagi awalan dan akhiran awalan baik di bawah awalan baik semasa ini bermakna subrentetan ini telah dipadankan sebelum ini, bukan Ia perlu untuk memadankan semula dan mula memadankan terus dari aksara seterusnya subrentetan.

Adakah kita perlu memadankan setiap watak setiap kali kita mengira seterusnya[i]? Bolehkah kita membuat kesimpulan berdasarkan seterusnya[i - 1] untuk mengurangkan perbandingan yang tidak perlu?

Dengan idea ini, mari kita lihat langkah berikut:

Anggap seterusnya[i - 1] = k - 1;

Jika modelStr[k] = modelStr [ i] kemudian seterusnya[i]=k

Jika modelStr[k] != modelStr[i], bolehkah kita terus menentukan seterusnya[i] = seterusnya[i - 1]?

Melalui contoh di atas, kita dapat melihat dengan jelas bahawa seterusnya[i]!=next[i-1], kemudian apabila modelStr[k]!=modelStr At [i ], kita sudah tahu seterusnya[0], seterusnya[1]...seterusnya[i-1], bagaimana hendak terbalik seterusnya[i]?

Andaikan modelStr[x…i] ialah subrentetan akhiran terpanjang yang boleh dipadankan oleh awalan dan akhiran, maka subrentetan awalan yang paling lama sepadan ialah modelStr[0…i-x]

Apabila kita menemui rentetan padanan terpanjang, rentetan padanan kedua terpanjang sebelumnya (tidak termasuk semasa i), iaitu modelStr[x…i-1] sepatutnya telah diselesaikan sebelum ini, jadi kita hanya perlu mencari rentetan padanan tertentu ini yang telah diselesaikan Anggapkan bahawa subrentetan awalan ialah modelStr[0…i-x-1], subrentetan akhiran ialah modelStr[x…i-1] dan modelStr[i-x] == modelStr [i], ini. subrentetan awalan dan akhiran ialah subrentetan awalan sekunder, ditambah dengan aksara semasa ialah subrentetan awalan dan akhiran yang paling lama padan.

Pelaksanaan kod

Pertama sekali, tatasusunan seterusnya yang paling penting dalam algoritma kmp ini menandakan bilangan aksara subrentetan awalan dan akhiran terpanjang sehingga subskrip semasa algoritma, jika Jika awalan tertentu adalah awalan yang baik, iaitu, ia sepadan dengan awalan rentetan corak, kita boleh menggunakan teknik tertentu untuk meluncur lebih daripada satu aksara ke hadapan. Lihat penjelasan sebelumnya untuk butiran. Kami tidak tahu terlebih dahulu yang merupakan awalan yang baik, dan proses pemadanan adalah lebih daripada sekali, jadi kami memanggil kaedah permulaan pada permulaan untuk memulakan tatasusunan seterusnya.

1 Jika aksara seterusnya bagi subrentetan awalan terpanjang bagi aksara sebelumnya == aksara semasa, subrentetan awalan terpanjang bagi aksara sebelumnya boleh ditambah terus kepada aksara semasa

2. .Jika tidak sama, anda perlu mencari aksara seterusnya bagi subrentetan awalan terpanjang sedia ada sebelum ini yang sama dengan subrentetan semasa, kemudian tetapkan subrentetan akhiran awalan terpanjang bagi subrentetan aksara semasa

int[] next ;
    /**
     * 初始化next数组
     * @param modelStr
     */
    public void init(char[] modelStr) {
        //首先计算next数组
        //遍历modelStr，遍历到的字符与之前字符组成一个串
        next = new int[modelStr.length];
        int start = 0;
        while (start < modelStr.length) {
            next[start] = this.recursion(start, modelStr);
            ++ start;
        }
    }

    /**
     *
     * @param i 当前遍历到的字符
     * @return
     */
    private int recursion(int i, char[] modelStr) {
        //next记录的是个数，不是下标
        if (0 == i) {
            return 0;
        }
        int last = next[i -1];
        //没有匹配的,直接判断第一个是否匹配
        if (0 == last) {
            if (modelStr[last] == modelStr[i]) {
                return 1;
            }
            return 0;
        }
        //如果last不为0，有值，可以作为最长匹配的前缀
        if (modelStr[last] == modelStr[i]) {
            return next[i - 1] + 1;
        }
        //当next[i-1]对应的子串的下一个值与modelStr不匹配时，需要找到当前要找的最长匹配子串的次长子串
        //依据就是次长子串对应的子串的下一个字符==modelStr[i];
        int tempIndex = i;
        while (tempIndex > 0) {
            last = next[tempIndex - 1];
            //找到第一个下一个字符是当前字符的匹配子串
            if (modelStr[last] == modelStr[i]) {
                return last + 1;
            }
            -- tempIndex;
        }
        return 0;
    }

dan kemudian mula menggunakannya. Tatasusunan seterusnya digunakan untuk memadankan bermula dari aksara pertama dan mencari aksara pertama yang tidak dipadankan ia adalah, ia dikembalikan terus Jika tidak, hakim Jika yang pertama tidak sepadan, ia akan dipadankan terus dengan yang kemudian. Jika terdapat awalan yang baik, tatasusunan seterusnya digunakan pada masa ini Melalui tatasusunan seterusnya, kita tahu di mana padanan semasa boleh bermula, dan tidak perlu memadankan yang sebelumnya.

public int kmp(char[] mainStr, char[] modelStr) {
        //开始进行匹配
        int i = 0, j = 0;
        while (i + modelStr.length <= mainStr.length) {
            while (j < modelStr.length) {
                //找到第一个不匹配的位置
                if (modelStr[j] != mainStr[i]) {
                    break;
                }
                ++ i;
                ++ j;
            }
            if (j == modelStr.length) {
                //证明完全匹配
                return i - j;
            }
            //走到这里找到的是第一个不匹配的位置
            if (j == 0) {
                ++ i;
                continue;
            }
            //从好前缀后一个匹配
            j = next[j - 1];
        }
        return -1;
    }

Atas ialah kandungan terperinci Apakah kaedah pelaksanaan algoritma KMP di Jawa?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!