Python melaksanakan lapan formula pengedaran kebarangkalian dan tutorial visualisasi data

Pengetahuan tentang kebarangkalian dan statistik adalah teras sains data dan pembelajaran mesin; kami memerlukan pengetahuan tentang statistik dan kebarangkalian untuk mengumpul, menyemak dan menganalisis data dengan berkesan.

Terdapat beberapa contoh fenomena dalam dunia nyata yang dianggap bersifat statistik (iaitu data cuaca, data jualan, data kewangan, dll.). Ini bermakna dalam beberapa kes kami telah dapat membangunkan kaedah yang membantu kami mensimulasikan alam semula jadi melalui fungsi matematik yang boleh menerangkan ciri-ciri data. "Taburan kebarangkalian ialah fungsi matematik yang memberikan kebarangkalian berlakunya hasil yang berbeza yang mungkin dalam eksperimen." Memahami pengedaran data membantu memodelkan dunia di sekeliling kita dengan lebih baik. Ia boleh membantu kami menentukan kemungkinan pelbagai hasil, atau menganggarkan kebolehubahan peristiwa. Semua ini menjadikan pemahaman taburan kebarangkalian berbeza sangat berharga dalam sains data dan pembelajaran mesin. Pengagihan seragamPengagihan yang paling langsung ialah pengedaran seragam. Taburan seragam ialah taburan kebarangkalian di mana semua hasil berkemungkinan sama. Sebagai contoh, jika kita melancarkan dadu yang adil, kebarangkalian untuk mendarat pada sebarang nombor ialah 1/6. Ini adalah pengagihan seragam diskret. Tetapi tidak semua pengagihan seragam adalah diskret - ia juga boleh berterusan. Mereka boleh mengambil sebarang nilai sebenar dalam julat yang ditentukan. Fungsi ketumpatan kebarangkalian (PDF) bagi taburan seragam berterusan antara a dan b adalah seperti berikut: Mari lihat cara mengekodnya dalam Python:

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()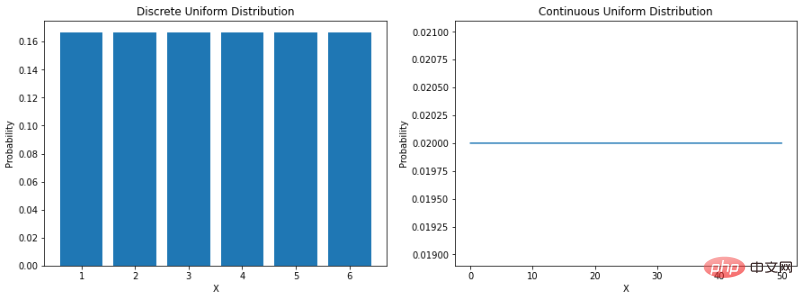

Taburan Gaussian

Pengedaran Gaussian mungkin merupakan pengedaran yang paling biasa didengar dan biasa. Ia mempunyai beberapa nama: ada yang memanggilnya keluk loceng kerana plot kebarangkaliannya kelihatan seperti loceng, ada yang memanggilnya taburan Gauss kerana ahli matematik Jerman Karl Gauss yang mula-mula menyifatkannya, dan yang lain lagi Ia diedarkan secara normal kerana ahli statistik awal menyedarinya. berlaku berulang kali. Fungsi ketumpatan kebarangkalian bagi taburan normal adalah seperti berikut: σ ialah sisihan piawai dan μ ialah min bagi taburan. Ambil perhatian bahawa dalam taburan normal, min, mod dan median semuanya sama. Apabila kita memplot pembolehubah rawak taburan normal, lengkung adalah simetri tentang min-separuh nilai berada di sebelah kiri pusat dan separuh di sebelah kanan pusat. Dan, jumlah kawasan di bawah lengkung ialah 1.

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()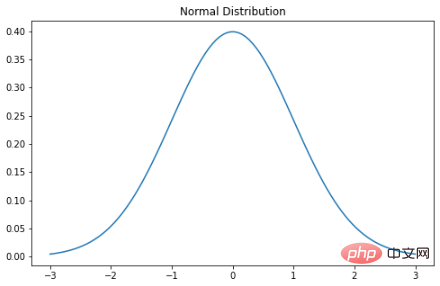

Untuk taburan normal. Peraturan praktikal memberitahu kami berapa peratusan data yang berada dalam bilangan sisihan piawai tertentu daripada min. Peratusannya ialah:

• 68% daripada data berada dalam satu sisihan piawai min.
• 95% daripada data termasuk dalam dua sisihan piawai min.
• 99.7% daripada data berada dalam tiga sisihan piawai min. ​

Taburan lognormal

Taburan lognormal ialah pembolehubah rawak berterusan dengan taburan kebarangkalian taburan lognormal. Oleh itu, jika pembolehubah rawak X diagihkan secara logik, maka Y = ln(X) mempunyai taburan normal. Berikut ialah PDF taburan lognormal: Pembolehubah rawak teragih lognormal hanya mengambil nilai nyata positif. Oleh itu, taburan lognormal mencipta lengkung condong ke kanan. Mari kita plot dalam Python:

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()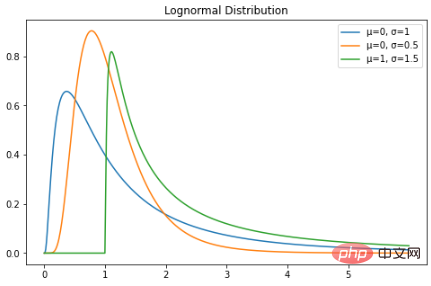

Taburan Poisson

Taburan Poisson dinamakan sempena nama ahli matematik Perancis Simon Denis Poisson. Ini ialah taburan kebarangkalian diskret, yang bermaksud bahawa ia mengira peristiwa dengan hasil terhingga - dengan kata lain, ia adalah taburan pengiraan. Oleh itu, taburan Poisson digunakan untuk menunjukkan bilangan kali peristiwa boleh berlaku dalam tempoh tertentu. Jika sesuatu peristiwa berlaku pada kadar tetap dalam masa, maka kebarangkalian untuk memerhati bilangan (n) peristiwa dalam masa boleh diterangkan dengan taburan Poisson. Sebagai contoh, pelanggan boleh tiba di kedai kopi pada kadar purata 3 kali seminit. Kita boleh menggunakan taburan Poisson untuk mengira kebarangkalian bahawa 9 pelanggan akan tiba dalam masa 2 minit. Berikut ialah formula fungsi jisim kebarangkalian: λ ialah kadar peristiwa dalam satu unit masa – dalam kes kami, ia ialah 3. k ialah bilangan kejadian - dalam kes kami, ia adalah 9. Scipy boleh digunakan di sini untuk melengkapkan pengiraan kebarangkalian.

from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3))

0.002700503931560479

Lengkung taburan Poisson adalah serupa dengan taburan normal, dan λ mewakili nilai puncak.

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()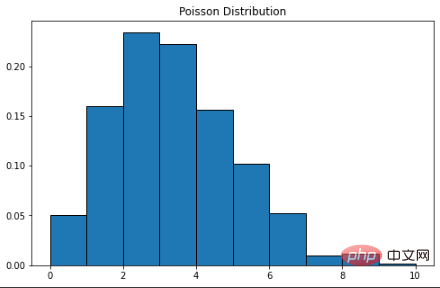

Taburan eksponen

指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下：λ 是速率参数，x 是随机变量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()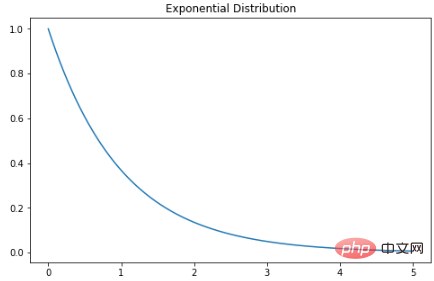

二项分布

可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布，每个实验都问一个是 - 否问题，每个实验都有自己的布尔值结果：成功或失败。本质上，二项分布测量两个事件的概率。一个事件发生的概率为 p，另一事件发生的概率为 1-p。这是二项分布的公式：

• P = 二项分布概率
• = 组合数
• x = n次试验中特定结果的次数
• p = 单次实验中，成功的概率
• q = 单次实验中，失败的概率
• n = 实验的次数

可视化代码如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()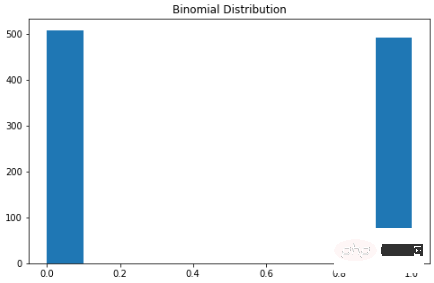

学生 t 分布

学生 t 分布（或简称 t 分布）是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特（William Sealy Gosset）以笔名“student”开发的。PDF如下：n 是称为“自由度”的参数，有时可以看到它被称为“d.o.f.” 对于较高的 n 值，t 分布更接近正态分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()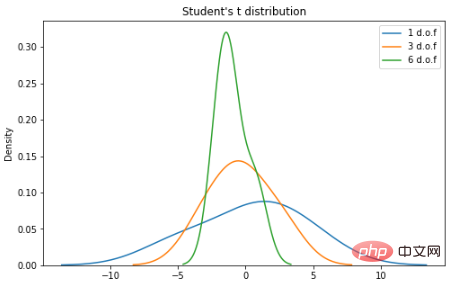

卡方分布

卡方分布是伽马分布的一个特例；对于 k 个自由度，卡方分布是一些独立的标准正态随机变量的 k 的平方和。PDF如下：这是一种流行的概率分布，常用于假设检验和置信区间的构建。在 Python 中绘制一些示例图：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()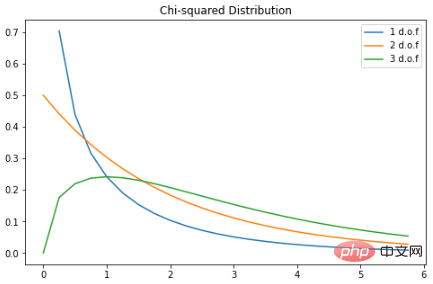

掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布，希望对你有所帮助。

Atas ialah kandungan terperinci Python melaksanakan lapan formula pengedaran kebarangkalian dan tutorial visualisasi data. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!