Rumah >Peranti teknologi >AI >Mesin Turing ialah rangkaian saraf berulang paling hangat RNN dalam pembelajaran mendalam? Kertas 1996 membuktikannya!
Mesin Turing ialah rangkaian saraf berulang paling hangat RNN dalam pembelajaran mendalam? Kertas 1996 membuktikannya!
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-25 21:25:06815semak imbas
Dari 19 hingga 23 Ogos 1996, Persidangan Kepintaran Buatan Finland yang dianjurkan oleh Persatuan Kepintaran Buatan Finland dan Universiti Vaasa telah diadakan di Vaasa, Finland.
Sebuah kertas kerja yang diterbitkan pada persidangan itu membuktikan bahawa mesin Turing adalah rangkaian saraf berulang.
Ya, ini 26 tahun yang lalu!
Mari kita lihat kertas kerja yang diterbitkan pada tahun 1996 ini.
1 Pengenalan
1.1 Klasifikasi Rangkaian Neural
Rangkaian saraf boleh digunakan untuk tugas pengelasan untuk menentukan sama ada corak input tergolong dalam kategori tertentu.
Telah lama diketahui bahawa rangkaian suapan hadapan satu lapisan hanya boleh digunakan untuk mengklasifikasikan corak boleh dipisahkan secara linear, iaitu, semakin banyak lapisan yang berturutan, semakin kompleks pengedaran kelas.
Apabila maklum balas diperkenalkan dalam struktur rangkaian, nilai output perceptron dikitar semula dan bilangan lapisan berturut-turut menjadi tidak terhingga pada dasarnya.
Adakah kuasa pengkomputeran telah dipertingkatkan secara kualitatif? Jawapannya ya.
Sebagai contoh, pengelas boleh dibina untuk menentukan sama ada integer input adalah perdana.
Ternyata saiz rangkaian yang digunakan untuk tujuan ini boleh terhad, dan walaupun saiz integer input tidak terhad, bilangan prima yang boleh dikelaskan dengan betul ialah tak terhingga.
Dalam artikel ini, "struktur rangkaian kitaran yang terdiri daripada elemen pengiraan yang sama" boleh digunakan untuk melengkapkan sebarang fungsi boleh dikira (secara algoritma).
1.2 Mengenai kebolehkiraan
Menurut aksiom asas teori kebolehkiraan, fungsi boleh dikira boleh dilaksanakan menggunakan mesin Turing.
Tentukan bahasa pengaturcaraan  . Bahasa ini mempunyai empat operasi asas:
. Bahasa ini mempunyai empat operasi asas:

Di sini, V mewakili sebarang pembolehubah dengan nilai integer positif, j mewakili sebarang nombor baris.
Ia boleh ditunjukkan bahawa jika fungsi Turing boleh dikira, ia boleh dikodkan menggunakan bahasa mudah ini (lihat [1] untuk butiran) .
2 Turing Network
2.1 Struktur Rangkaian Neural Rekursif
Rangkaian saraf yang dikaji dalam artikel ini terdiri daripada perceptron, dan kesemuanya mempunyai sama Struktur 🎜> perwakilan) dikira menggunakan input n
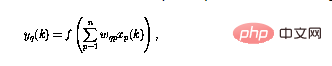
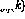 Fungsi tak linear f kini boleh ditakrifkan sebagai
Fungsi tak linear f kini boleh ditakrifkan sebagai 
supaya fungsinya adalah Nilai negatif hanya boleh "dipotong", dan gelung dalam rangkaian perceptron bermakna bahawa perceptron boleh digabungkan dengan cara yang kompleks.
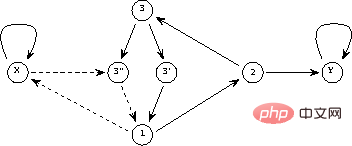
Rajah 1 Rangka kerja keseluruhan rangkaian saraf berulang, struktur adalah autonomi tanpa input luaran, dan tingkah laku rangkaian ditentukan sepenuhnya oleh keadaan awal
Dalam Rajah 1, struktur rekursif ditunjukkan dalam rangka kerja umum: sekarang 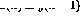 dan n ialah bilangan perceptron, dan sambungan dari perceptron p ke perceptron q diberikan oleh
dan n ialah bilangan perceptron, dan sambungan dari perceptron p ke perceptron q diberikan oleh 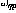 Perwakilan berat skalar.
Perwakilan berat skalar.
Iaitu, diberi keadaan awal, keadaan rangkaian akan berulang sehingga ia tidak lagi berubah, dan hasilnya boleh dibaca pada keadaan stabil ini atau pada "titik tetap" rangkaian.
2.2 Pembinaan Rangkaian Neural
Seterusnya, kami akan menerangkan bagaimana program 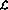 dilaksanakan dalam rangkaian perceptron. Rangkaian terdiri daripada nod (atau perceptron berikut):
dilaksanakan dalam rangkaian perceptron. Rangkaian terdiri daripada nod (atau perceptron berikut):
-
Untuk setiap pembolehubah V dalam atur cara, terdapat nod pembolehubah
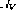 .
. -
Untuk setiap baris program i, terdapat nod arahan
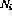 .
. -
Untuk setiap arahan cawangan bersyarat dalam talian i, terdapat dua nod cawangan tambahan
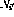 dan
dan 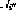 .
.
Bahasa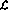 Pelaksanaan program termasuk perubahan berikut pada rangkaian perceptron:
Pelaksanaan program termasuk perubahan berikut pada rangkaian perceptron:
- Untuk program Bagi setiap pembolehubah dalam V, gunakan pautan berikut untuk mengembangkan rangkaian:

-
Jika kod program Jika tiada operasi dalam talian i (
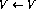 ), pautan berikut digunakan untuk mengembangkan rangkaian (dengan mengandaikan bahawa nod
), pautan berikut digunakan untuk mengembangkan rangkaian (dengan mengandaikan bahawa nod  wujud:
wujud:

-
Jika terdapat operasi tambahan () pada baris i
 , kembangkan rangkaian sebagai berikut:
, kembangkan rangkaian sebagai berikut:

-
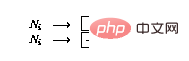
Jika terdapat operasi pengurangan () dalam baris i
 , kembangkan rangkaian seperti berikut:
, kembangkan rangkaian seperti berikut:
-
Jika talian i mempunyai cawangan bersyarat (
 ), kembangkan rangkaian seperti berikut:
), kembangkan rangkaian seperti berikut:
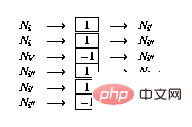
2.3 Equivalence Proof
Apa yang perlu dibuktikan sekarang ialah "keadaan dalaman rangkaian atau kandungan nod rangkaian" boleh dikenal pasti oleh program keadaan, dan rangkaian Kesinambungan keadaan sepadan dengan aliran program.
mentakrifkan "keadaan undang-undang" rangkaian seperti berikut:
-
kepada semua nod peralihan
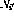 dan Keluaran
dan Keluaran 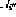 (seperti yang ditakrifkan dalam 2.2) ialah sifar (
(seperti yang ditakrifkan dalam 2.2) ialah sifar ( paling banyak); satu nod arahan
paling banyak); satu nod arahan
- mempunyai output unit (
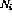 ), semua nod arahan lain mempunyai output sifar, dan
), semua nod arahan lain mempunyai output sifar, dan 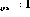 nod pembolehubah mempunyai nilai keluaran integer bukan negatif.
nod pembolehubah mempunyai nilai keluaran integer bukan negatif.
- Jika output semua nod arahan adalah sifar, maka nyatakan keadaan akhir
, kaunter atur cara berada pada baris i dan nilai pembolehubah yang sepadan ialah disimpan dalam nod pembolehubah. Perubahan dalam status rangkaian diaktifkan oleh nod bukan sifar.
Mula-mula, memfokuskan pada nod pembolehubah, ternyata mereka berkelakuan seperti penyepadu, dengan kandungan nod sebelumnya digelung kembali ke nod yang sama.
Satu-satunya sambungan daripada nod boleh ubah ke nod lain mempunyai pemberat negatif - itulah sebabnya nod yang mengandungi sifar tidak berubah, disebabkan oleh bukan lineariti (2).
Seterusnya, nod arahan diterangkan secara terperinci. Andaikan bahawa satu-satunya nod arahan bukan sifar
adalah pada masa k---ini sepadan dengan pembilang atur cara pada baris i dalam kod program. Jika baris i
dalam program ialah, maka tingkah laku hadapan rangkaian boleh dinyatakan sebagai ( Sahaja nod terjejas ditunjukkan)
Ternyata status rangkaian baharu itu sah semula. Berbanding dengan kod atur cara, ini sepadan dengan kaunter atur cara yang dialihkan ke baris 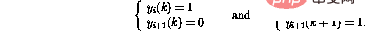 i+1
i+1
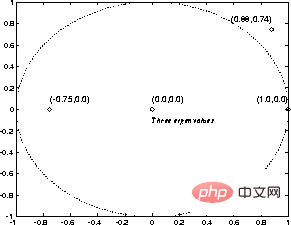
Sebaliknya, jika baris i dalam program adalah Dengan cara ini, selain mengalihkan pembilang program ke baris seterusnya, nilai pembolehubah V juga akan dikurangkan. Jika baris i ialah Operasi cawangan bersyarat (JIKA GOTO Akhir sekali, Ternyata dalam Selepas langkah ini, keadaan rangkaian sekali lagi boleh ditafsirkan sebagai petikan atur cara yang lain. Nilai pembolehubah telah ditukar dan token telah dialihkan ke lokasi baharu seolah-olah baris program yang sepadan telah dilaksanakan. Jika token hilang, keadaan rangkaian tidak lagi berubah - ini hanya boleh berlaku jika pembilang program "melebihi" kod program, yang bermaksud program ditamatkan. Pengendalian rangkaian juga serupa dengan pengendalian program yang sepadan, dan buktinya telah selesai. Adalah mudah untuk menentukan arahan diperkemas tambahan yang menjadikan pengaturcaraan lebih mudah, Dan yang dihasilkan program lebih mudah dibaca dan dilaksanakan dengan lebih pantas. Sebagai contoh, cawangan tanpa syarat (GOTO j) pada baris i Kaedah di atas sama sekali tidak bermakna pelaksanaan mesin Turing satu-satunya cara. Ini adalah pelaksanaan yang mudah dan mungkin tidak semestinya optimum dalam aplikasi. Pembinaan di atas juga boleh dilaksanakan dalam bentuk matriks. Idea asas adalah untuk menyimpan nilai pembolehubah dan "pembilang program" dalam keadaan proses s, dan biarkan matriks peralihan keadaan A mewakili pautan nod antara. Kendalian struktur matriks boleh ditakrifkan sebagai proses dinamik masa diskret di mana fungsi bernilai vektor tak linear Kandungan matriks peralihan keadaan A mudah dinyahkod daripada formula rangkaian - elemen matriks ialah pemberat antara nod. Formula matriks ini serupa dengan rangka kerja "matriks konsep" yang dicadangkan dalam [3]. Andaikan anda ingin melaksanakan fungsi mudah y=x, iaitu pembolehubah input x Nilai hendaklah dihantar kepada pembolehubah output y. Menggunakan bahasa ditunjukkan dalam Rajah 2. Garis pepejal mewakili sambungan positif (berat 1), dan garis putus-putus mewakili sambungan negatif (berat -1 ). Berbanding dengan Rajah 1, struktur rangkaian dilukis semula dan dipermudahkan dengan menyepadukan elemen kelewatan dalam nod. Rajah 2 Pelaksanaan rangkaian program ringkas dalam bentuk matriks , program di atas kelihatan seperti Dua baris/lajur pertama dalam matriks A sepadan dengan sambungan untuk mewakili kedua-dua Pautan kepada nod pembolehubah Y dan X, tiga baris seterusnya mewakili tiga baris program (1, 2 dan 3), dua baris terakhir mewakili nod tambahan yang diperlukan untuk arahan cawangan (3' dan 3''). Kemudian awal (sebelum lelaran) dan akhir (selepas lelaran, apabila titik tetap ditemui) menyatakan Jika nilai nod pembolehubah akan dikekalkan dengan ketat antara 0 dan 1, operasi sistem dinamik (3) akan menjadi linear dan fungsi akan mempunyai tiada kesan langsung. Pada dasarnya, teori sistem linear kemudiannya boleh digunakan dalam analisis. Contohnya, dalam Rajah 3, nilai eigen bagi matriks peralihan keadaan A ditunjukkan. Walaupun terdapat nilai eigen di luar bulatan unit dalam contoh di atas, ketaklinearan menjadikan lelaran sentiasa stabil. Ternyata lelaran sentiasa menumpu selepas langkah Rajah 3 "Nilai eigen" program ringkas Hasilnya menunjukkan bahawa mesin Turing boleh dikodkan sebagai rangkaian perceptron. Secara takrifan, semua fungsi boleh dikira boleh dikira Turing - dalam rangka kerja teori kebolehkiraan, tiada sistem pengiraan yang lebih berkuasa wujud. Itulah sebabnya, boleh disimpulkan - Rangkaian perceptron berulang (ditunjukkan di atas) ialah mesin Turing (satu lagi ) bentuk. Kelebihan kesetaraan ini ialah hasil teori kebolehkiraan mudah diperoleh - contohnya, memandangkan rangkaian dan keadaan awal, adalah mustahil untuk menilai proses Adakah ia akhirnya akan berhenti. Persamaan teori di atas tidak menyatakan apa-apa tentang kecekapan pengiraan. Mekanisme berbeza yang berlaku dalam rangkaian boleh menjadikan beberapa fungsi dilaksanakan dengan lebih baik dalam rangka kerja ini berbanding dengan pelaksanaan mesin Turing tradisional (yang sebenarnya adalah komputer hari ini). Sekurang-kurangnya dalam beberapa kes, contohnya, pelaksanaan rangkaian bagi algoritma boleh disejajarkan dengan membenarkan berbilang "pembilang program" dalam vektor syot kilat. Pengendalian rangkaian adalah setempat, bukan global. Timbul persoalan menarik, contohnya, sama ada masalah NP-lengkap boleh diserang dengan lebih berkesan dalam persekitaran rangkaian! Berbanding dengan bahasa Berbanding dengan kod program asal, formula matriks jelas merupakan perwakilan maklumat yang lebih "berterusan" daripada kod program - parameter boleh diubah suai (selalunya), tetapi keputusan lelaran tidak akan berubah secara tiba-tiba. "Lebihan" ini mungkin berguna dalam sesetengah aplikasi. Sebagai contoh, apabila menggunakan algoritma genetik (GA) untuk pengoptimuman struktur, strategi carian rawak yang digunakan dalam algoritma genetik boleh dibuat lebih cekap: selepas struktur sistem berubah, berterusan kos boleh dicari Minima tempatan fungsi menggunakan beberapa teknik tradisional (lihat [4]). Mempelajari struktur mesin keadaan terhingga melalui contoh, seperti yang diterangkan dalam [5], boleh diketahui bahawa kaedah meningkatkan struktur rangkaian secara berulang juga digunakan dalam situasi yang lebih kompleks ini. Bukan sahaja teori rangkaian saraf boleh mendapat manfaat daripada keputusan di atas - hanya melihat formula sistem dinamik (3), jelas sekali semua fenomena yang terdapat dalam bidang teori kebolehkiraan juga diwakili oleh wujud mudah Borang - mencari proses dinamik bukan linear. Sebagai contoh, ketidakpastian masalah terhenti adalah sumbangan yang menarik kepada bidang teori sistem: untuk sebarang proses keputusan yang diwakili sebagai mesin Turing, terdapat sistem dinamik dalam bentuk (3) yang melanggar proses ini - Tidak mungkin untuk membina algoritma analisis kestabilan am untuk cth. Terdapat beberapa persamaan antara struktur rangkaian yang dibentangkan dan paradigma rangkaian neural Hopfield rekursif (lihat, cth. [2] ). Dalam kedua-dua kes, "input" dikodkan sebagai keadaan awal dalam rangkaian, dan "output" dibaca daripada keadaan akhir rangkaian selepas lelaran. Titik tetap rangkaian Hopfield ialah model corak yang telah diprogramkan dan inputnya ialah corak "bunyi" - rangkaian boleh digunakan untuk meningkatkan corak yang rosak. Pandangan (2) bagi fungsi tak linear dalam Berbanding dengan rangkaian Hopfield di mana output unit sentiasa -1 atau 1, dapat dilihat bahawa, secara teori, struktur rangkaian ini sangat berbeza. Sebagai contoh, walaupun set titik stabil dalam rangkaian Hopfield adalah terhad, program yang diwakili oleh rangkaian Turing selalunya mempunyai bilangan hasil yang mungkin tidak terhingga. Keupayaan pengiraan rangkaian Hopfield dibincangkan dalam [6]. Petri net ialah alat yang berkuasa untuk pemodelan sistem berasaskan peristiwa dan serentak [7]. Jaring Petri terdiri daripada bit dan peralihan serta lengkok yang menghubungkannya. Setiap tempat mungkin mengandungi sebarang bilangan token, dan pengedaran token dipanggil tanda jaring Petri. Jika semua kedudukan input transformasi diduduki oleh penanda, transformasi mungkin mencetuskan, mengalih keluar penanda daripada setiap lokasi inputnya dan menambah penanda pada setiap lokasi outputnya. Boleh dibuktikan bahawa jaring Petri yang dilanjutkan dengan arka penekan tambahan juga mempunyai keupayaan mesin Turing (lihat [7]). Perbezaan utama antara jaring Turing yang disebutkan di atas dan jaring Petri ialah rangka kerja jaring Petri adalah lebih kompleks dan mempunyai struktur yang disesuaikan khas, yang tidak boleh dinyatakan dengan bentuk am yang mudah (3). Rujukan 1 Davis, M. and Weyuker, E.: Computability, Kerumitan, dan Bahasa---Fundamentals of Theoretical Computer Press, New York, 1983. 2 Haykin, S.: A Comprehensive College Publishing. New York, 1994. 3 Hyötyniemi, H.: Correlations---Building Blocks of Intelligence? 1995, ms. 199--226. 4 Hyötyniemi, H. dan Koivo, H.: Gen, Kod, dan Sistem Dinamik Dalam Prosiding Bengkel Nordic Kedua tentang Algoritma Genetik (NWGA'96), Vaasa, Finland, 19--23 Ogos 1996. 5 Manolios, P. dan Fanelli, R.: Rangkaian Neural Berulang Urutan Pertama dan Terhad Deterministik State Automata. 6, 1994, ms. 1155--1173. 6 Orponen, P.: Kuasa Pengiraan Jaring Hopfield Diskret dengan Unit Tersembunyi 8. 1996 , ms 403--415. 7 Peterson, J.L.: Petri Net Theory and the Modelling of Systems Prentice--Hall, Englewood Cliffs, New Jersey, 1981. Rujukan: https://www.php.cn/link/ 0465a1824942fac18343451281834512834345 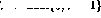 , maka tingkah laku satu langkah ke hadapan ialah
, maka tingkah laku satu langkah ke hadapan ialah 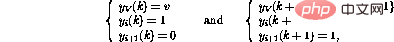
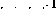 , operasi rangkaian akan sama kecuali nilai pembolehubah V dinaikkan .
, operasi rangkaian akan sama kecuali nilai pembolehubah V dinaikkan . 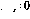 j) dalam talian i mengaktifkan Urutan operasi yang lebih kompleks :
j) dalam talian i mengaktifkan Urutan operasi yang lebih kompleks : 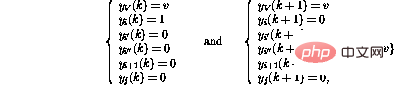
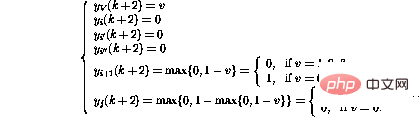
3 Pengubahsuaian
3.1 Sambungan
3.2 Rumusan matriks
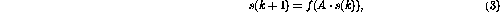
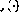 kini ditakrifkan mengikut unsur seperti dalam (2).
kini ditakrifkan mengikut unsur seperti dalam (2). 4 Contoh
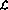 ini boleh dikodkan sebagai (supaya "titik masuk" kini bukan baris pertama tetapi baris ketiga):
ini boleh dikodkan sebagai (supaya "titik masuk" kini bukan baris pertama tetapi baris ketiga): 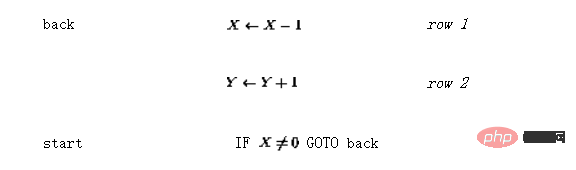
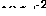 , di mana
, di mana 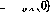 .
. 
5 Perbincangan
5.1 Aspek Teori
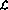 , pelaksanaan rangkaian mempunyai "sambungan" berikut:
, pelaksanaan rangkaian mempunyai "sambungan" berikut:
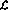 , di mana semua nombor yang diwakili adalah nombor rasional.
, di mana semua nombor yang diwakili adalah nombor rasional.
5.2 Kerja Berkaitan
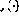 menjadikan bilangan keadaan yang mungkin dalam "Rangkaian Turing" di atas tidak terhingga.
menjadikan bilangan keadaan yang mungkin dalam "Rangkaian Turing" di atas tidak terhingga.
Atas ialah kandungan terperinci Mesin Turing ialah rangkaian saraf berulang paling hangat RNN dalam pembelajaran mendalam? Kertas 1996 membuktikannya!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

