Bagaimana untuk melaksanakan penapis Bloom di Java

BitMap

Komputer moden menggunakan binari (bit, bit) sebagai unit asas maklumat 1 bait adalah bersamaan dengan 8 bit Contohnya, bigSebuah rentetan terdiri daripada 3 bait, tetapi dalam realiti Apabila komputer menyimpannya, ia dinyatakan dalam perduaan Kod ASCII yang sepadan bagi big masing-masing ialah 98, 105, dan 103, dan nombor perduaan yang sepadan ialah 01100010, 01101001 dan 01100111.

Banyak bahasa pembangunan menyediakan fungsi bit operasi Penggunaan bit yang betul boleh meningkatkan penggunaan memori dan kecekapan pembangunan.

Idea asas Bit-map ialah menggunakan bit untuk menandakan nilai yang sepadan dengan elemen, dan kuncinya ialah elemen. Memandangkan data disimpan dalam unit bit, ruang storan boleh disimpan dengan banyak.

Di Java, int menduduki 4 bait, 1 bait = 8 bit (1 bait = 8 bit), jika kita menggunakan nilai setiap 32 bit ini untuk mewakili nombor, ia adalah Jika tidak, ia boleh mewakili 32 nombor Dalam erti kata lain, 32 nombor hanya memerlukan ruang yang diduduki oleh int, yang boleh mengurangkan ruang sebanyak 32 kali.

1 Byte = 8 Bit, 1 KB = 1024 Byte, 1 MB = 1024 KB, 1GB = 1024 MB

Anggapkan bahawa tapak web itu mempunyai 100 juta pengguna yang melawat secara bebas setiap hari Terdapat 50 juta pengguna Jika jenis koleksi dan BitMap digunakan untuk menyimpan pengguna aktif setiap hari:

1 Jika id pengguna adalah jenis int, 4 bait, 32 bit, jenis koleksi menduduki 50,000 ruang. 000 * 4/1024/1024 = 200M;

Jadi bagaimana untuk menggunakan BitMap untuk mewakili nombor?

Seperti yang dinyatakan di atas, bit bit digunakan untuk menandakan nilai yang sepadan dengan elemen, dan kuncinya ialah elemen Kita boleh bayangkan BitMap sebagai

array

dengan bit sebagai unit unit hanya boleh menyimpan 0 dan 1 (0 bermakna nombor tidak wujud, 1 bermakna ia wujud), dan subskrip tatasusunan dipanggil offset dalam BitMap. Sebagai contoh, kita perlu mewakili empat nombor seperti berikut: {1,3,5,7}

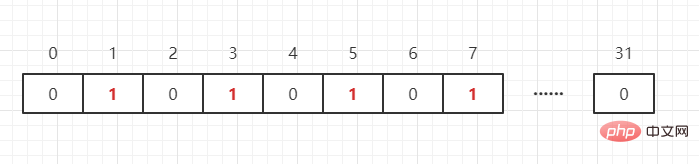Bagaimana jika ada nombor 65 lagi? Anda hanya perlu membuka

tatasusunan int untuk menyimpan data ini (di mana N mewakili nilai maksimum dalam kumpulan data ini), iaitu:

int[N/32+1]

: boleh mewakili 0~31

int[0]

: boleh mewakili 32~63

int[1]

: boleh mewakili 64~95

int[2]

Katakan kita ingin menentukan sama ada sebarang integer adalah dalam senarai , kemudian

akan mendapat subskrip dan

akan mengetahui di mana ia berada dalam subskrip, seperti: M/32M%32

,

, iaitu, 65 ialah yang pertama kedudukan dalam 65/32 = 2 . 65%32=1int[2]Penapis Bloom

Pada asasnya, penapis Bloom ialah struktur data, struktur data kebarangkalian yang agak bijak, dicirikan oleh sisipan dan pertanyaan yang cekap, yang boleh digunakan untuk memberitahu anda " Sesuatu mesti tidak wujud atau mungkin wujud”.

Berbanding dengan struktur data tradisional seperti Senarai, Set, Peta, dll., ia lebih cekap dan mengambil sedikit ruang, tetapi kelemahannya ialah hasil yang dipulangkan adalah kebarangkalian, tidak tepat.

Malah, penapis Bloom digunakan secara meluas dalam

sistem senarai hitam laman web

, sistem penapisan spam, sistem penentuan berat URL perayap, dsb. Pangkalan data teragih terkenal Google Bigtable menggunakan penapis Bloom untuk mencari baris atau lajur yang tidak wujud untuk mengurangkan bilangan carian cakera IO pelayar Google Chrome menggunakan penapis Bloom untuk mempercepatkan perkhidmatan penyemakan imbas yang selamat. Penapis Bloom juga digunakan dalam banyak sistem Nilai-Kekunci untuk mempercepatkan proses pertanyaan, seperti Hbase, Accumulo, Leveldb Secara umumnya, Nilai disimpan dalam cakera dan mengakses cakera memerlukan banyak masa Walau bagaimanapun, penapis Bloom boleh digunakan untuk menentukan dengan cepat sama ada Nilai yang sepadan dengan Kunci wujud, begitu banyak operasi IO cakera yang tidak perlu boleh dielakkan.

Petakan elemen menjadi titik dalam tatasusunan bit (Bit Array) melalui fungsi Hash. Dengan cara ini, kita hanya perlu melihat sama ada titik adalah 1 untuk mengetahui sama ada ia berada dalam set. Ini adalah idea asas penapis Bloom.

Senario Aplikasi

1 Pada masa ini terdapat 1 bilion nombor asli, disusun dalam keadaan tidak teratur, dan ia perlu diisih. Sekatan dilaksanakan pada mesin 32-bit, dan had memori ialah 2G. Bagaimana ia dilakukan?

2. Bagaimana untuk mencari dengan cepat sama ada alamat URL berada dalam senarai hitam? (Setiap URL purata 64 bait)

3. Adakah anda perlu menganalisis tingkah laku log masuk pengguna untuk menentukan aktiviti pengguna?

4. Perangkak web-bagaimana untuk menentukan sama ada URL telah dirangkak?

5. Cari atribut pengguna (senarai hitam, senarai putih, dll.) dengan cepat?

6. Data disimpan pada cakera, bagaimana untuk mengelakkan sejumlah besar IO tidak sah?

7. Tentukan sama ada unsur wujud dalam berbilion data?

8.

Kelemahan struktur data tradisional

Secara umumnya, adalah OK untuk menyimpan URL halaman web dalam pangkalan data untuk carian atau membuat jadual cincang untuk carian.

Apabila jumlah data adalah kecil, adalah wajar untuk berfikir seperti ini Nilai itu sememangnya boleh dipetakan ke Kunci HashMap, dan kemudian hasilnya boleh dikembalikan dalam kerumitan masa O(1), yang mana. adalah amat cekap. Walau bagaimanapun, pelaksanaan HashMap juga mempunyai kekurangan, seperti bahagian kapasiti storan yang tinggi Memandangkan kewujudan faktor beban, biasanya ruang tidak boleh digunakan sepenuhnya Sebagai contoh, jika 10 juta HashMap, Key=String (panjang tidak melebihi 16 aksara, dan Sangat sedikit kebolehulangan), Value=Integer, berapa banyak ruang yang akan diduduki? 1.2G.

Malah, menggunakan bitmap, 10 juta jenis int hanya memerlukan kira-kira 40M (10 000 000 * 4/1024/1024 =40M) ruang, menyumbang 3%. , menyumbang 13.3%.

Ia boleh dilihat bahawa apabila anda mempunyai banyak nilai, seperti ratusan juta, saiz memori yang diduduki oleh HashMap boleh dibayangkan.

Tetapi jika keseluruhan sistem senarai hitam halaman web mengandungi 10 bilion URL halaman web, carian dalam pangkalan data adalah sangat memakan masa, dan jika setiap ruang URL adalah 64B, maka memori 640GB diperlukan untuk umum pelayan untuk mencapai keperluan ini.

Prinsip Pelaksanaan

Andaikan kita mempunyai set A, dan terdapat n elemen dalam A. Menggunakan fungsi k pencincangan , setiap elemen dalam A dipetakan ke kedudukan berbeza dalam tatasusunan B dengan panjang bit, dan nombor perduaan pada kedudukan ini Kedua-duanya ditetapkan kepada 1 . Jika elemen yang hendak disemak dipetakan oleh fungsi cincang k ini dan didapati bahawa nombor perduaan dalam kedudukan knya semuanya 1, elemen ini berkemungkinan tergolong dalam set A. Jika tidak, Mesti tidak tergolong dalam set A.

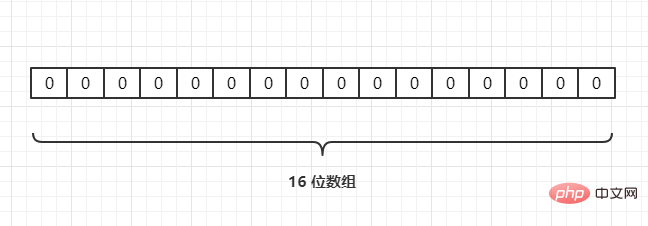
Sebagai contoh, kami mempunyai 3 URL {URL1,URL2,URL3}, dan petakannya kepada tatasusunan panjang 16 melalui fungsi cincang, seperti berikut:

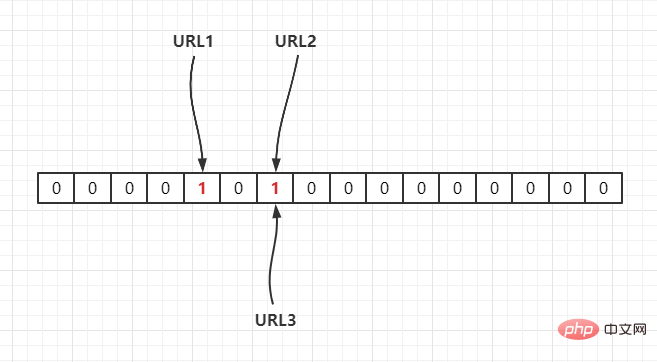
Jika Fungsi cincang semasa ialah Hash2(), yang dipetakan ke tatasusunan melalui operasi cincangan Andaikan Hash2(URL1) = 3, Hash2(URL2) = 6, Hash2(URL3) = 6, seperti berikut:

. Oleh itu, Jika kita perlu menentukan sama ada URL1 berada dalam set ini, kemudian hitung subskripnya melalui Hash(1), dan dapatkan nilainya Jika ia adalah 1, ia bermakna ia wujud.

Disebabkan konflik cincang dalam Hash, seperti yang ditunjukkan di atas, URL2,URL3 terletak pada satu kedudukan dengan mengandaikan bahawa fungsi Hash adalah baik, jika panjang tatasusunan kami ialah m mata, maka jika kami ingin mengurangkan kadar konflik Contohnya, 1%, jadual cincang ini hanya boleh memuatkan elemen m/100 Jelas sekali, kadar penggunaan ruang menjadi rendah, iaitu mustahil untuk mencapai cekap ruang . (cekap ruang).

Penyelesaiannya juga mudah, iaitu menggunakan berbilang algoritma Hash Jika salah seorang daripada mereka mengatakan bahawa elemen itu tiada dalam set, ia pasti tiada, seperti berikut:

Hash2(URL1) = 3,Hash3(URL1) = 5,Hash4(URL1) = 6
Hash2(URL2) = 5,Hash3(URL2) = 8,Hash4(URL2) = 14
Hash2(URL3) = 4,Hash3(URL3) = 7,Hash4(URL3) = 10

<.>

Fenomena salah sangka

Pendekatan di atas juga mempunyai masalah, kerana semakin banyak nilai ditambah, semakin banyak bit akan ditetapkan kepada 1, jadi walaupun jika nilai tertentu tidak disimpan, tetapi jika tiga bit yang dikembalikan oleh fungsi cincang semuanya ditetapkan kepada 1 oleh nilai lain, program akan tetap menentukan bahawa nilai ini wujud. Sebagai contoh, jika terdapat

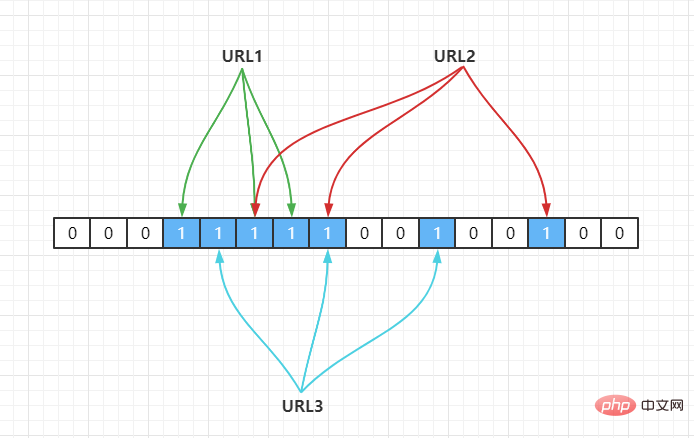
yang tidak wujud pada masa ini, selepas pengiraan hash, didapati bit bit adalah seperti berikut: URL1000

Hash2(URL1000) = 7,Hash3(URL1000) = 8,Hash4(URL1000) = 14

Tetapi bit bit di atas telah

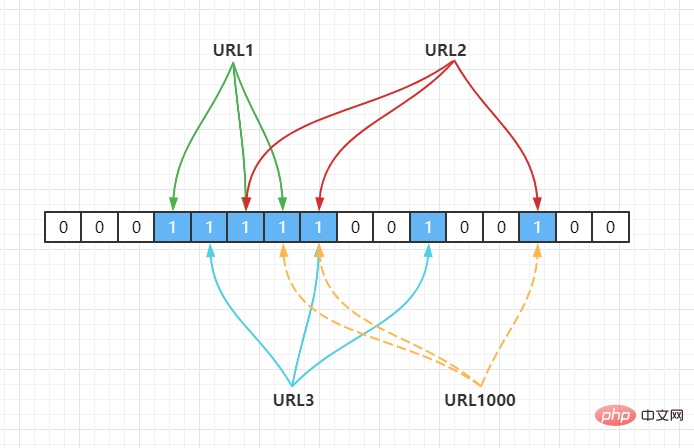
ditetapkan kepada 1, dan atur cara akan menentukan bahawa nilai URL1,URL2,URL3 wujud. URL1000

Ini adalah fenomena salah penilaian penapis Bloom Oleh itu,

Apa yang dinilai oleh penapis Bloom mungkin tidak wujud, tetapi apa yang dinilainya tidak wujud mestilah tidak wujud.

Penapis Bloom boleh mewakili set dengan tepat dan menentukan dengan tepat sama ada sesuatu elemen berada dalam set ini Ketepatannya ditentukan oleh reka bentuk khusus pengguna. Tetapi kelebihan penapis Bloom ialah

ia boleh mencapai kadar ketepatan yang lebih tinggi menggunakan ruang yang sangat sedikit.

Laksanakan

Peta bit Redis

dan laksanakannya berdasarkan arahan berkaitan struktur data peta bit redis.

RedisBloom

Penapis Bloom boleh dilaksanakan menggunakan operasi bitmap dalam Redis sehingga versi Redis 4.0 menyediakan fungsi pemalam yang penapis Bloom yang disediakan secara rasmi oleh Redis secara rasmi. , penapis Bloom dimuatkan ke dalam Pelayan Redis sebagai pemalam Laman web rasmi mengesyorkan RedisBloom sebagai Modul penapis Redis Bloom.

Guava’s BloomFilter

Apabila projek Guava mengeluarkan versi 11.0, salah satu ciri yang baru ditambah ialah kelas BloomFilter.

Redisson

Lapisan asas Redisson melaksanakan penapis bloom berdasarkan peta bit.

public static void main(String[] args) {
    Config config = new Config();
    // 单机环境
    config.useSingleServer().setAddress("redis://192.168.153.128:6379");
    //构造Redisson
    RedissonClient redisson = Redisson.create(config);
    RBloomFilter<String> bloomFilter = redisson.getBloomFilter("nameList");
    //初始化布隆过滤器：预计元素为100000000L,误差率为3%,根据这两个参数会计算出底层的 bit 数组大小
    bloomFilter.tryInit(100000L, 0.03);
    //将 10086 插入到布隆过滤器中
    bloomFilter.add("10086");
    //判断下面号码是否在布隆过滤器中
    System.out.println(bloomFilter.contains("10086"));//true
    System.out.println(bloomFilter.contains("10010"));//false
    System.out.println(bloomFilter.contains("10000"));//false
}

解决缓存穿透

缓存穿透是指查询一个根本不存在的数据，缓存层和存储层都不会命中，如果从存储层查不到数据则不写入缓存层。

缓存穿透将导致不存在的数据每次请求都要到存储层去查询，失去了缓存保护后端存储的意义。缓存穿透问题可能会使后端存储负载加大，由于很多后端存储不具备高并发性，甚至可能造成后端存储宕掉。

因此我们可以用布隆过滤器来解决，在访问缓存层和存储层之前，将存在的 key 用布隆过滤器提前保存起来，做第一层拦截。

例如：一个推荐系统有 4 亿个用户 id，每个小时算法工程师会根据每个用户之前历史行为计算出推荐数据放到存储层中，但是最新的用户由于没有历史行为，就会发生缓存穿透的行为，为此可以将所有推荐数据的用户做成布隆过滤器。如果布隆过滤器认为该用户 id 不存在，那么就不会访问存储层，在一定程度保护了存储层。

注：布隆过滤器可能会误判，放过部分请求，当不影响整体，所以目前该方案是处理此类问题最佳方案

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan penapis Bloom di Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!