Bagaimana untuk melaksanakan graf tidak terarah di Jawa?

Konsep asas

Takrifan graf

Sesuatu graf terdiri daripada set titik V={v_i} dan satu set pasangan unsur tidak tertib dalam VV E={e_k} membentuk kumpulan binari, direkodkan sebagai G=(V,E), unsur v_{i dipanggil bucu, dan unsur e}k _{dalam E dipanggil tepi.}

Untuk dua titik u, v dalam V, jika tepi (u, v) milik E, maka dua titik u dan v dikatakan bersebelahan, dan u dan v dipanggil titik akhir bagi tepi (u, v) .

Kita boleh menggunakan m(G)=|E| untuk mewakili bilangan tepi dalam graf G, dan n(G)=|V|.

Takrif graf tidak berarah

Untuk mana-mana tepi (vi, vj) dalam E, jika titik akhir tepi (vi, vj) tidak tertib, ia adalah tepi tidak berarah Pada masa ini Graf G dipanggil graf tidak berarah. Graf tidak berarah ialah model graf yang paling ringkas Rajah berikut menunjukkan graf tidak berarah yang sama Bucu diwakili oleh bulatan, dan tepi ialah sambungan antara bucu tanpa anak panah (gambar daripada "Algoritma Edisi Ke-4"):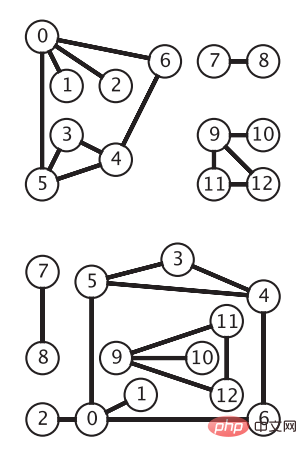

API Graf Tidak Berhala

Untuk graf tidak berarah, kami mengambil berat tentang bilangan bucu, bilangan tepi, jumlah bucu bersebelahan bagi setiap bucu tepi, jadi antara muka adalah seperti berikut:

package com.zhiyiyo.graph;

/**
 * 无向图
 */
public interface Graph {
    /**
     * 返回图中的顶点数
     */
    int V();

    /**
     * 返回图中的边数
     */
    int E();

    /**
     * 向图中添加一条边
     * @param v 顶点 v
     * @param w 顶点 w
     */
    void addEdge(int v, int w);

    /**
     * 返回所有相邻顶点
     * @param v 顶点 v
     * @return 所有相邻顶点
     */
    Iterable<Integer> adj(int v);
}

Pelaksanaan graf tidak berarah

Matriks bersebelahan

Gunakan matriks untuk mewakili pasangan graf untuk mengkaji sifat graf dan Aplikasi ini selalunya lebih mudah. ​​Terdapat pelbagai perwakilan matriks untuk pelbagai graf, seperti matriks berat dan matriks bersebelahan. Ia ditakrifkan sebagai:

Untuk graf G=(V,E), |V|=n, bina matriks A=(a

ij₎n×n_{, di mana:}

maka matriks A dipanggil matriks bersebelahan graf G.

Ia boleh dilihat daripada definisi bahawa kita boleh menggunakan tatasusunan Boolean dua dimensi

untuk melaksanakan matriks bersebelahan Apabila A ia bermakna bucu A[i][j] = true dan i adalah bersebelahan. . j

Untuk graf G dengan n bucu, ruang yang digunakan oleh matriks bersebelahan ialah n

2 ^{nilai Boolean, yang akan menyebabkan banyak pembaziran untuk graf jarang apabila bilangan bucu Apabila ia sangat besar, ruang yang digunakan akan menjadi angka astronomi. Pada masa yang sama, apabila graf adalah istimewa dan mempunyai gelung diri dan tepi selari, perwakilan matriks bersebelahan tidak berkuasa. "Algoritma" memberikan graf dengan dua situasi ini:}

Susun tepi

Untuk graf tidak terarah, kita boleh melaksanakan kelas

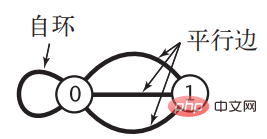
, hanya dua contoh pembolehubah digunakan untuk menyimpan dua bucu u dan v, dan kemudian semua Edge boleh disimpan dalam tatasusunan. Terdapat masalah besar dengan ini, iaitu, apabila mendapatkan semua bucu bersebelahan bucu v, anda mesti merentasi keseluruhan tatasusunan untuk mendapatkannya Kerumitan masa ialah O(|E|) Memandangkan mendapatkan bucu bersebelahan adalah operasi yang sangat biasa , Cara menyatakannya ini juga tidak berkesan. Edge

Susun atur senarai bersebelahan

Jika kita mewakili bucu sebagai integer dengan julat nilai 0∼|V|&tolak;1, maka kita boleh menggunakan tatasusunan panjang |V| Indeks mewakili setiap bucu, dan setiap elemen tatasusunan kemudiannya ditetapkan kepada senarai terpaut yang mana bucu lain yang bersebelahan dengan bucu yang diwakili oleh indeks dipasang. Graf tidak berarah yang ditunjukkan dalam Rajah 1 boleh diwakili oleh tatasusunan senarai bersebelahan yang ditunjukkan dalam rajah di bawah:

Kod untuk menggunakan senarai bersebelahan untuk melaksanakan graf tidak terarah adalah seperti berikut, memandangkan Setiap senarai terpaut dalam tatasusunan senarai bersebelahan akan menyimpan bucu bersebelahan dengan bucu, jadi apabila menambah tepi pada graf, anda perlu menambah nod pada dua senarai terpaut dalam tatasusunan:

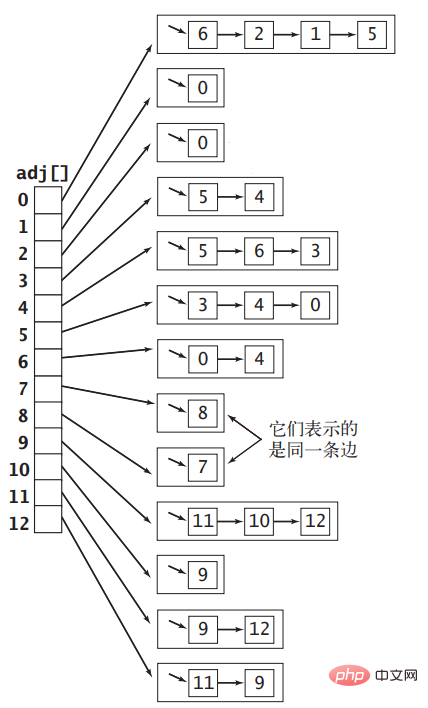
package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;

/**
 * 使用邻接表实现的无向图
 */
public class LinkGraph implements Graph {
    private final int V;
    private int E;
    private LinkStack<Integer>[] adj;

    public LinkGraph(int V) {
        this.V = V;
        adj = (LinkStack<Integer>[]) new LinkStack[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new LinkStack<>();
        }
    }

    @Override
    public int V() {
        return V;
    }

    @Override
    public int E() {
        return E;
    }

    @Override
    public void addEdge(int v, int w) {
        adj[v].push(w);
        adj[w].push(v);
        E++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

Gunakan di sini Kod tindanan adalah seperti berikut Pelaksanaan tindanan bukanlah fokus blog ini, jadi saya tidak akan menerangkan terlalu banyak di sini:

package com.zhiyiyo.collection.stack;

import java.util.EmptyStackException;
import java.util.Iterator;

/**
 * 使用链表实现的堆栈
 */
public class LinkStack<T> {
    private int N;
    private Node first;

    public void push(T item) {
        first = new Node(item, first);
        N++;
    }

    public T pop() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        N--;
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    public Iterator<T> iterator() {
        return new ReverseIterator();
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }


    private class ReverseIterator implements Iterator<T> {
        private Node node = first;

        @Override
        public boolean hasNext() {
            return node != null;
        }

        @Override
        public T next() {
            T item = node.item;
            node = node.next;
            return item;
        }

        @Override
        public void remove() {
        }
    }
}

Perjalanan graf tidak terarah

<.>Memandangkan graf berikut A kini diperlukan untuk mencari laluan dari setiap bucu ke bucu 0. Bagaimana untuk mencapai ini? Atau secara mudahnya, diberi bucu 0 dan 4, ia diperlukan untuk menentukan sama ada bermula dari bucu 0 boleh mencapai bucu 4. Bagaimana untuk mencapai ini? Ini memerlukan penggunaan dua kaedah traversal graf: carian mendalam-dahulu dan carian luas-dahulu.

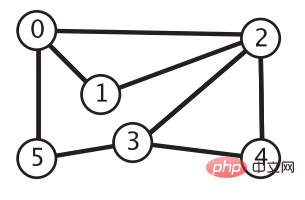Sebelum memperkenalkan dua kaedah traversal ini, mari kita berikan API yang perlu dilaksanakan untuk menyelesaikan masalah di atas:

package com.zhiyiyo.graph;

public interface Search {
    /**
     * 起点 s 和 顶点 v 之间是否连通
     * @param v 顶点 v
     * @return 是否连通
     */
    boolean connected(int v);

    /**
     * 返回与顶点 s 相连通的顶点个数（包括 s）
     */
    int count();

    /**
     * 是否存在从起点 s 到顶点 v 的路径
     * @param v 顶点 v
     * @return 是否存在路径
     */
    boolean hasPathTo(int v);

    /**
     * 从起点 s 到顶点 v 的路径，不存在则返回 null
     * @param v 顶点 v
     * @return 路径
     */
    Iterable<Integer> pathTo(int v);
}

深度优先搜索

深度优先搜索的思想类似树的先序遍历。我们从顶点 0 开始，将它的相邻顶点 2、1、5 加到栈中。接着弹出栈顶的顶点 2，将它相邻的顶点 0、1、3、4 添加到栈中，但是写到这你就会发现一个问题：顶点 0 和 1明明已经在栈中了，如果还把他们加到栈中，那这个栈岂不是永远不会变回空。所以还需要维护一个数组 boolean[] marked，当我们将一个顶点 i 添加到栈中时，就将 marked[i] 置为 true，这样下次要想将顶点 i 加入栈中时，就得先检查一个 marked[i] 是否为 true，如果为 true 就不用再添加了。重复栈顶节点的弹出和节点相邻节点的入栈操作，直到栈为空，我们就完成了顶点 0 可达的所有顶点的遍历。

为了记录每个顶点到顶点 0 的路径，我们还需要一个数组 int[] edgeTo。每当我们访问到顶点 u 并将其一个相邻顶点 i 压入栈中时，就将 edgeTo[i] 设置为 u，说明要想从顶点i 到达顶点 0，需要先回退顶点 u，接着再从顶点 edgeTo[u] 处获取下一步要回退的顶点直至找到顶点 0。

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;


public class DepthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public DepthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        dfs();
    }

    /**
     * 递归实现的深度优先搜索
     *
     * @param v 顶点 v
     */
    private void dfs(int v) {
        marked[v] = true;
        N++;
        for (int i : graph.adj(v)) {
            if (!marked[i]) {
                edgeTo[i] = v;
                dfs(i);
            }
        }
    }

    /**
     * 堆栈实现的深度优先搜索
     */
    private void dfs() {
        Stack<Integer> vertexes = new LinkStack<>();
        vertexes.push(s);
        marked[s] = true;

        while (!vertexes.isEmpty()) {
            Integer v = vertexes.pop();
            N++;

            // 将所有相邻顶点加到堆栈中
            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    vertexes.push(i);
                }
            }
        }
    }

    @Override
    public boolean connected(int v) {
        return marked[v];
    }

    @Override
    public int count() {
        return N;
    }

    @Override
    public boolean hasPathTo(int v) {
        return connected(v);
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new LinkStack<>();

        int vertex = v;
        while (vertex != s) {
            path.push(vertex);
            vertex = edgeTo[vertex];
        }

        path.push(s);
        return path;
    }
}

广度优先搜索

广度优先搜索的思想类似树的层序遍历。与深度优先搜索不同，从顶点 0 出发，广度优先搜索会先处理完所有与顶点 0 相邻的顶点 2、1、5 后，才会接着处理顶点 2、1、5 的相邻顶点。这个搜索过程就是一圈一圈往外扩展、越走越远的过程，所以可以用来获取顶点 0 到其他节点的最短路径。只要将深度优先搜索中的堆换成队列，就能实现广度优先搜索：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;

public class BreadthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public BreadthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        bfs();
    }

    private void bfs() {
        LinkQueue<Integer> queue = new LinkQueue<>();
        marked[s] = true;
        queue.enqueue(s);

        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            N++;

            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    queue.enqueue(i);
                }
            }
        }
    }
}

队列的实现代码如下：

package com.zhiyiyo.collection.queue;


import java.util.EmptyStackException;


public class LinkQueue<T> {
    private int N;
    private Node first;
    private Node last;

    public void enqueue(T item) {
        Node node = new Node(item, null);
        if (++N == 1) {
            first = node;
        } else {
            last.next = node;
        }
        last = node;
    }

    public T dequeue() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        if (--N == 0) {
            last = null;
        }
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan graf tidak terarah di Jawa?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!