Apakah kaedah traversal rekursif dan bukan rekursif bagi pokok binari Java?

Kata Pengantar

Kaedah traversal pokok binari dibahagikan kepada traversal pra-tertib, traversal tertib, traversal seterusnya dan traversal aras.

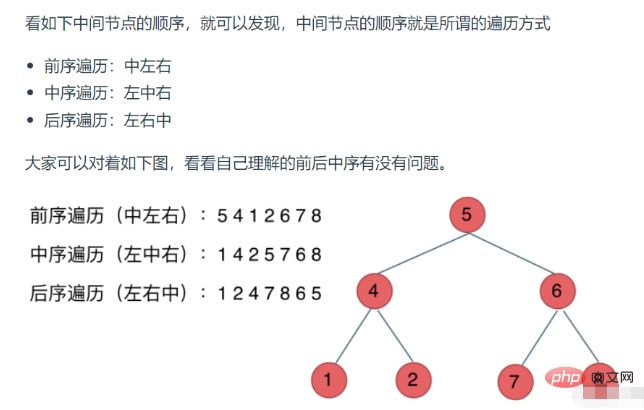
1. Rekursif traversal

Untuk rekursi, kita perlu bercakap tentang tiga elemen rekursi: foreorder traversal sebagai contoh

Masukan parameter rekursif Parameter dan nilai pulangan

Kerana anda ingin mencetak nilai nod yang dilalui dalam prapesanan, anda perlu memasukkan nilai nod dalam Senarai dalam parameter Selain daripada ini , tidak perlu memproses sebarang data dan tidak perlu mempunyai nilai pulangan , jadi jenis pemulangan fungsi rekursif adalah tidak sah, kodnya adalah seperti berikut:

public void preorder(TreeNode root, List<Integer> result)

Tentukan penamatan. keadaan

Dalam proses rekursi, bagaimana untuk mengira penghujung rekursi Sudah tentu, nod yang dilalui pada masa ini adalah Jika ia kosong, maka tahap rekursi ini akan berakhir, jadi jika yang dilalui pada masa ini? nod kosong, hanya kembalikan

if (root == null) return;

Logik gelung lapisan tunggal

Preorder traversal ialah tertib kiri dan kanan sederhana, jadi logik rekursi peringkat tunggal adalah mengambil nilai terlebih dahulu nod tengah. Kodnya adalah seperti berikut:

result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);

// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
    public List preorderTraversal(TreeNode root) {
        List result = new ArrayList();
        preorder(root, result);
        return result;
    }
    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);//先保存中间节点
        preorder(root.left, result); //处理左边节点
        preorder(root.right, result); //处理右边节点
    }
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
    public List inorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        inorder(root, res);
        return res;
    }
    void inorder(TreeNode root, List list) {
        if (root == null) {
            return;
        }
        inorder(root.left, list); //先处理左边节点
        list.add(root.val);       //保存中间当前的节点
        inorder(root.right, list);//先处理右边节点
    }
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
    public List postorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        postorder(root, res);
        return res;
    }
    void postorder(TreeNode root, List list) {
        if (root == null) {
            return;
        }
        postorder(root.left, list);  //先处理左边节点
        postorder(root.right, list); //再处理右边节点
        list.add(root.val);          //保存最后  
    }
}

2. Bukan lelaran

//前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack();
        if (root == null) return res;
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            res.add(node.val);
            if (node.right != null) { //先将右孩子入栈，因为它在最后
                stack.push(node.right);
            }
            if (node.left != null) { //左孩子入栈再出栈
                stack.push(node.left);
            }
        }
        return res;
    }
}
//中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;
        Stack<TreeNode> stack = new Stack();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            //如果可以，一直往左下探
            if (cur != null) {
                stack.push(cur);
                cur = cur.left;
            } else {
                cur = stack.pop(); //弹出来的肯定是叶子节点或中间节点
                res.add(cur.val); //将这个节点加入list
                cur = cur.right; //查看当前节点是否有右节点，如果右，肯定是中间节点，如果没有，就是叶子节点，继续弹出就可以
            }
        }
        return res;
    }
}
//后序遍历
//再来看后序遍历，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;
        Stack<TreeNode> stack = new Stack();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            res.add(node.val);
            if (node.left != null) stack.push(node.left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node.right != null) stack.push(node.right);// 空节点不入栈 
        }
        Collections.reverse(res); // 将结果反转之后就是左右中的顺序了
        return res;
    }
}

3 .Kaedah lelaran seragam untuk pokok binari

//前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null) st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}
//中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null) st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}
//后序遍历
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null) st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）         
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}

Atas ialah kandungan terperinci Apakah kaedah traversal rekursif dan bukan rekursif bagi pokok binari Java?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!