Rumah >Peranti teknologi >AI >Perbandingan teknologi pengurangan dimensi biasa: analisis kebolehlaksanaan untuk mengurangkan dimensi data sambil mengekalkan integriti maklumat
Perbandingan teknologi pengurangan dimensi biasa: analisis kebolehlaksanaan untuk mengurangkan dimensi data sambil mengekalkan integriti maklumat
- 王林ke hadapan
- 2023-04-23 18:46:081380semak imbas
Artikel ini akan membandingkan keberkesanan pelbagai teknik pengurangan dimensi pada data jadual dalam tugasan pembelajaran mesin. Kami menggunakan kaedah pengurangan dimensi pada set data dan menilai keberkesanannya melalui analisis regresi dan klasifikasi. Kami menggunakan kaedah pengurangan dimensi pada pelbagai set data yang diperoleh daripada UCI yang berkaitan dengan domain yang berbeza. Sebanyak 15 set data telah dipilih, 7 daripadanya akan digunakan untuk regresi dan 8 untuk pengelasan.
Untuk menjadikan artikel ini mudah dibaca dan difahami, hanya prapemprosesan dan analisis satu set data ditunjukkan. Percubaan bermula dengan memuatkan set data. Set data dibahagikan kepada set latihan dan ujian dan kemudian dinormalkan untuk mempunyai min 0 dan sisihan piawai 1.
Teknik pengurangan dimensi kemudian digunakan pada data latihan dan set ujian diubah untuk pengurangan dimensi menggunakan parameter yang sama. Untuk regresi, analisis komponen utama (PCA) dan penguraian nilai tunggal (SVD) digunakan untuk pengurangan dimensi Sebaliknya, untuk klasifikasi, analisis diskriminasi linear (LDA) digunakan
Selepas pengurangan dimensi, mesin berbilang. model pembelajaran dilatih Ujian telah dijalankan dan prestasi model yang berbeza dibandingkan pada set data berbeza yang diperoleh melalui kaedah pengurangan dimensi yang berbeza.
Mari kita mulakan proses dengan memuatkan dataset pertama,
import pandas as pd ## for data manipulation df = pd.read_excel(r'RegressionAirQualityUCI.xlsx') print(df.shape) df.head()

Dataset mengandungi 15 lajur, satu daripadanya ialah label yang diramalkan. Sebelum meneruskan pengurangan dimensi, lajur tarikh dan masa juga dialih keluar.
X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1) y = df['CO(GT)'] X.shape, y.shape #Output: ((9357, 12), (9357,))
Untuk latihan, kita perlu membahagikan set data kepada set latihan dan set ujian, supaya keberkesanan kaedah pengurangan dimensi dan model pembelajaran mesin yang dilatih pada ruang ciri pengurangan dimensi dapat dinilai. Model akan dilatih menggunakan set latihan dan prestasi akan dinilai menggunakan set ujian.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) X_train.shape, X_test.shape, y_train.shape, y_test.shape #Output: ((7485, 12), (1872, 12), (7485,), (1872,))
Sebelum menggunakan teknik pengurangan dimensi pada set data, data input boleh diskalakan untuk memastikan semua ciri berada pada skala yang sama. Ini penting untuk model linear kerana beberapa kaedah pengurangan dimensi boleh mengubah outputnya bergantung pada sama ada data dinormalkan dan sensitif kepada saiz ciri.
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) X_train.shape, X_test.shape
Analisis Komponen Utama (PCA)
Kaedah PCA pengurangan dimensi linear mengurangkan dimensi data sambil mengekalkan varians data sebanyak mungkin.
Kaedah PCA modul Python sklearn.decomposition akan digunakan di sini. Bilangan komponen untuk dikekalkan ditentukan melalui parameter ini dan nombor ini mempengaruhi bilangan dimensi yang disertakan dalam ruang ciri yang lebih kecil. Sebagai alternatif, kami boleh menetapkan varians sasaran untuk dikekalkan, yang menetapkan bilangan komponen berdasarkan jumlah varians dalam data yang ditangkap, yang kami tetapkan di sini kepada 0.95
from sklearn.decomposition import PCA pca = PCA(n_compnotallow=0.95) X_train_pca = pca.fit_transform(X_train) X_test_pca = pca.transform(X_test) X_train_pca

Apakah yang diwakili oleh ciri-ciri di atas? Walaupun ini boleh membantu dengan operasi tertentu, ia juga boleh menjadikan data lebih sukar untuk difahami. , PCA boleh mengenal pasti paksi baharu dalam data yang merupakan gabungan linear bagi ciri awal.
Penguraian Nilai Tunggal (SVD)
SVD ialah teknik pengurangan dimensi linear yang menayangkan ciri dengan varians data yang kecil ke dalam ruang dimensi rendah. Kita perlu menetapkan bilangan komponen untuk dikekalkan selepas pengurangan dimensi. Di sini kita akan mengurangkan dimensi sebanyak 2/3.
from sklearn.decomposition import TruncatedSVD svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33)) X_train_svd = svd.fit_transform(X_train) X_test_svd = svd.transform(X_test) X_train_svd

Melatih model regresi
Sekarang, kami akan mula melatih model menggunakan tiga jenis data di atas (set data asal, PCA dan SVD ) dan ujian, dan kami menggunakan berbilang model untuk perbandingan.
import numpy as np from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import SVR from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor from sklearn.metrics import r2_score, mean_squared_error import time
train_test_ML: Fungsi ini akan menyelesaikan tugasan berulang yang berkaitan dengan latihan dan ujian model. Prestasi semua model dinilai dengan mengira rmse dan r2_score. dan mengembalikan set data dengan semua butiran dan nilai yang dikira. Ia juga akan mencatat masa yang diambil oleh setiap model untuk melatih dan menguji set data masing-masing.
def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken'])
for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
r2 = np.round(r2_score(y_test, y_pred), 2)
rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken]
return temp_dfData asal:
original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test)
original_df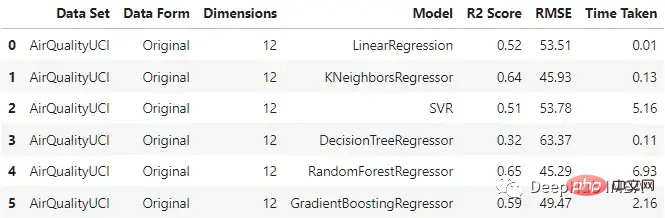
Dapat dilihat bahawa regressor KNN dan hutan rawak menunjukkan prestasi yang agak baik apabila memasukkan data asal, rawak The masa latihan di dalam hutan adalah yang paling lama.
PCA
pca_df = train_test_ML('AirQualityUCI', 'PCA Reduced', X_train_pca, y_train, X_test_pca, y_test)
pca_df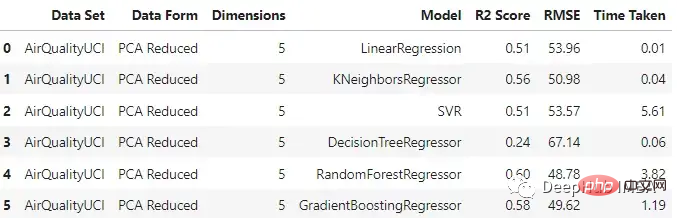
与原始数据集相比,不同模型的性能有不同程度的下降。梯度增强回归和支持向量回归在两种情况下保持了一致性。这里一个主要的差异也是预期的是模型训练所花费的时间。与其他模型不同的是,SVR在这两种情况下花费的时间差不多。
SVD
svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test)
svd_df
与PCA相比,SVD以更大的比例降低了维度,随机森林和梯度增强回归器的表现相对优于其他模型。
回归模型分析
对于这个数据集,使用主成分分析时,数据维数从12维降至5维,使用奇异值分析时,数据降至3维。
- 就机器学习性能而言,数据集的原始形式相对更好。造成这种情况的一个潜在原因可能是,当我们使用这种技术降低维数时,在这个过程中会发生信息损失。
- 但是线性回归、支持向量回归和梯度增强回归在原始和PCA案例中的表现是一致的。
- 在我们通过SVD得到的数据上,所有模型的性能都下降了。
- 在降维情况下,由于特征变量的维数较低,模型所花费的时间减少了。
将类似的过程应用于其他六个数据集进行测试,得到以下结果:
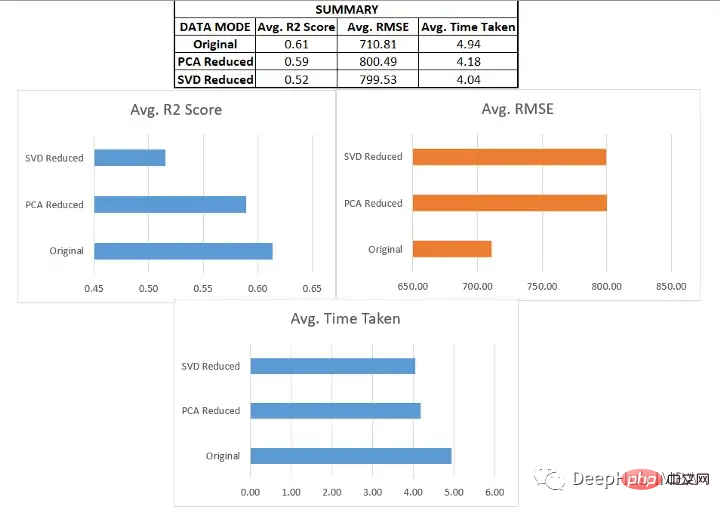
我们在各种数据集上使用了SVD和PCA,并对比了在原始高维特征空间上训练的回归模型与在约简特征空间上训练的模型的有效性
- 原始数据集始终优于由降维方法创建的低维数据。这说明在降维过程中可能丢失了一些信息。
- 当用于更大的数据集时,降维方法有助于显著减少数据集中的特征数量,从而提高机器学习模型的有效性。对于较小的数据集,改影响并不显著。
- 模型的性能在original和pca_reduced两种模式下保持一致。如果一个模型在原始数据集上表现得更好,那么它在PCA模式下也会表现得更好。同样,较差的模型也没有得到改进。
- 在SVD的情况下,模型的性能下降比较明显。这可能是n_components数量选择的问题,因为太小数量肯定会丢失数据。
- 决策树在SVD数据集时一直是非常差的,因为它本来就是一个弱学习器
训练分类模型
对于分类我们将使用另一种降维方法:LDA。机器学习和模式识别任务经常使用被称为线性判别分析(LDA)的降维方法。这种监督学习技术旨在最大化几个类或类别之间的距离,同时将数据投影到低维空间。由于它的作用是最大化类之间的差异,因此只能用于分类任务。
from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score
继续我们的训练方法
def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken'])
for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
accuracy = np.round(accuracy_score(y_test, y_pred), 2)
f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2)
recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2)
precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken]
return temp_df开始训练
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda = LinearDiscriminantAnalysis() X_train_lda = lda.fit_transform(X_train, y_train) X_test_lda = lda.transform(X_test)
预处理、分割和数据集的缩放,都与回归部分相同。在对8个不同的数据集进行新联后我们得到了下面结果:
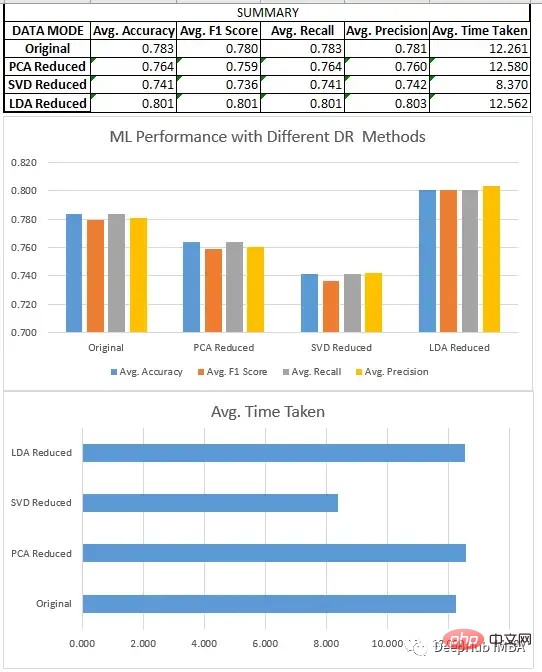
分类模型分析
我们比较了上面所有的三种方法SVD、LDA和PCA。
- LDA数据集通常优于原始形式的数据和由其他降维方法创建的低维数据,因为它旨在识别最有效区分类的特征的线性组合,而原始数据和其他无监督降维技术不关心数据集的标签。
- 降维技术在应用于更大的数据集时,可以极大地减少了数据集中的特征数量,这提高了机器学习模型的效率。在较小的数据集上,影响不是特别明显。除了LDA(它在这些情况下也很有效),因为它们在一些情况下,如二元分类,可以将数据集的维度减少到只有一个。
- 当我们在寻找一定的性能时,LDA可以是分类问题的一个非常好的起点。
- SVD与回归一样,模型的性能下降很明显。需要调整n_components的选择。
总结
我们比较了一些降维技术的性能,如奇异值分解(SVD)、主成分分析(PCA)和线性判别分析(LDA)。我们的研究结果表明,方法的选择取决于特定的数据集和手头的任务。
Untuk tugasan regresi, kami mendapati bahawa PCA umumnya berprestasi lebih baik daripada SVD. Dalam kes pengelasan, LDA mengatasi SVD dan PCA, serta set data asal. Adalah penting bahawa Analisis Diskriminasi Linear (LDA) secara konsisten mengalahkan Analisis Komponen Utama (PCA) dalam tugas pengelasan, tetapi ini tidak bermakna LDA ialah teknik yang lebih baik secara umum. Ini kerana LDA ialah algoritma pembelajaran terselia yang bergantung pada data berlabel untuk mencari ciri yang paling diskriminatif dalam data, manakala PCA ialah teknik tanpa seliaan yang tidak memerlukan data berlabel dan berusaha untuk mengekalkan sebanyak mungkin varians. Oleh itu, PCA mungkin lebih sesuai untuk tugasan yang tidak diselia atau situasi di mana kebolehtafsiran adalah kritikal, manakala LDA mungkin lebih sesuai untuk tugas yang melibatkan data berlabel.
Walaupun teknik pengurangan dimensi boleh membantu mengurangkan bilangan ciri dalam set data dan meningkatkan kecekapan model pembelajaran mesin, adalah penting untuk mempertimbangkan potensi kesan pada prestasi model dan kebolehtafsiran hasil.
Kod lengkap artikel ini:
https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb
Atas ialah kandungan terperinci Perbandingan teknologi pengurangan dimensi biasa: analisis kebolehlaksanaan untuk mengurangkan dimensi data sambil mengekalkan integriti maklumat. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

