Bagaimana untuk melaksanakan pilih atur penuh dalam algoritma Java

Algoritma 1

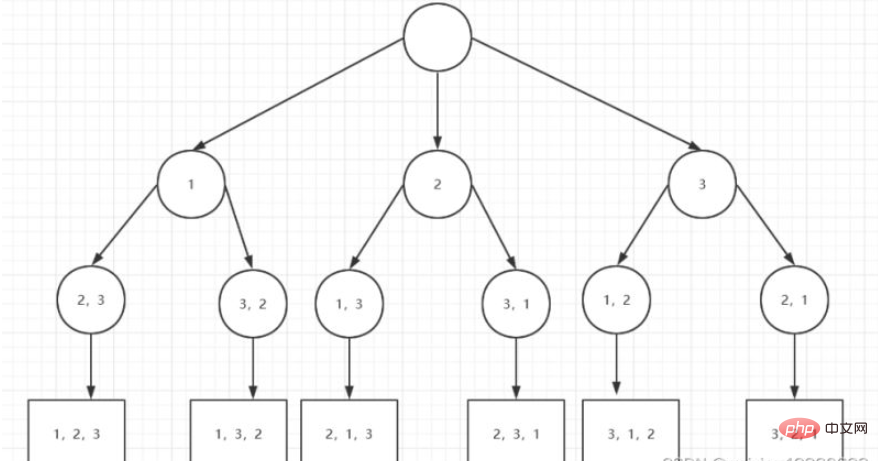
Dilaksanakan berdasarkan rekursi dan backtracking. Apabila menyusun 1, 2, dan 3, mula-mula kembali dari 3 kepada 2 dan mendapati bahawa tiada situasi lain yang mungkin, kemudian kembali ke 1, susun 1, 3, 2, dan kemudian naik semula apabila terdapat situasi lain. , iaitu, nod akar, dan kemudian Apabila menyusun 2 sebagai kedudukan pertama, ulangi proses di atas untuk meletakkan semua keputusan yang mungkin ke dalam res.

Kod:

import java.util.ArrayList;
import java.util.List;
 
public class h718_1 {
 
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
        int[] arr = {1,2,3};
 
        h718_1 h2 = new h718_1();
        h2.dfs(arr,new ArrayList<>());
        for (List<Integer> re : res) {
            System.out.println(re);
        }
 
    }
 
    public List<List<Integer>> dfs( int[] arr,List<Integer> list){
        List<Integer> temp = new ArrayList<>(list);
        if (arr.length == list.size()){
            res.add(temp);
        }
        for (int i=0;i<arr.length;i++){
            if (temp.contains(arr[i])){
                continue;
            }
            temp.add(arr[i]);
            dfs(arr,temp);
            temp.remove(temp.size()-1);
        }
        return res;
    }
 
}

Algoritma 2

Mencapai pilihatur penuh dengan menukar kedudukan: Andaikan set ialah {1, 2, 3 , 4};

Kedudukan swap gelung: swap 1 dan 2; swap 1 dan 3; 🎜>

Contohnya: pertukaran pertama 1 dan 1 menentukan bahawa 1 berada di tempat pertama, jadi ia boleh dianggap sebagai {1} + pertukaran rekursif {2,3,4};

Tempat pertama Pertukaran pertama 1 dan 2 menentukan bahawa 2 berada di tempat pertama, jadi ia boleh dianggap sebagai {2} + pertukaran rekursif {1,3,4};

Pertukaran pertama 1 dan 3 menentukan bahawa 3 berada di tempat pertama Jadi ia boleh dilihat sebagai {3} + pertukaran rekursif {1,2,4};

Pertukaran pertama 1 dan 4 menentukan bahawa 4 berada di yang pertama. tempat, jadi ia boleh dilihat sebagai {4} + pertukaran rekursif {1 ,2,3};

dan seterusnya.

Kod:

Algoritma 3

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
public class h718_2 {
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
 
        int[] arr = {1,2,3};
        h718_2 h3 = new h718_2();
        h3.pailie_swap(0,arr);
 
    }
    public void pailie_swap(int index, int[] arr){
        if (arr.length==index){
            System.out.println(Arrays.toString(arr));
            return;
        }
        for (int i = index;i<arr.length;i++){
            swap(i,index,arr);
            pailie_swap(index+1,arr);
            swap(i,index,arr);
        }
 
    }
 
    public void swap(int i,int j ,int[] arr){
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
 
    }
}

Anda boleh mencapai susunan penuh dengan menambahkan elemen:

Mula-mula tentukan senarai dan letakkan elemen pertama untuk ; dan kemudian masukkan elemen yang selebihnya ke dalam semua kemungkinan kedudukan elemen set sebelumnya untuk menjana senarai baharu; Mula-mula takrifkan senarai dan tambah elemen pertama sebagai {1}; kemudian elemen kedua 2 boleh dimasukkan ke dalam dua kedudukan sebelum dan selepas {1} untuk membentuk senarai baharu: {21, 12}, dan elemen ketiga 3 ialah dimasukkan ke dalam elemen senarai masing-masing Semua kedudukan ialah: {321, 231, 213, 312, 132, 123} dan seterusnya.

Kod:

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan pilih atur penuh dalam algoritma Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!