Pemodelan kembar digital berdasarkan pembelajaran mesin dan pengoptimuman terhad

Penterjemah |. Zhu Xianzhong

Penilai |. sistem atau proses fizikal dunia sebenar dan boleh digunakan untuk simulasi dan ramalan gelagat input, pemantauan, penyelenggaraan, perancangan, dsb. Walaupun kembar digital seperti bot perkhidmatan pelanggan kognitif adalah perkara biasa dalam aplikasi harian, dalam artikel ini saya akan membandingkan dua jenis berbeza untuk pemodelan dengan menggambarkan dua jenis kembar digital yang berbeza dalam teknik sains data Kembar industri.

Dua bidang sains data yang digunakan secara meluas bagi kembar digital yang dibincangkan dalam artikel ini adalah seperti berikut:

a) Analisis Diagnostik dan Ramalan:

Dalam kaedah analisis ini, diberikan siri A input yang digunakan oleh kembar digital untuk mendiagnosis punca atau meramalkan kelakuan masa depan sistem. Model pembelajaran mesin berasaskan IoT digunakan untuk mencipta mesin dan kilang pintar. Model ini membolehkan input sensor dianalisis dalam masa nyata untuk mendiagnosis, meramal dan mencegah masalah dan kegagalan masa hadapan sebelum ia berlaku.

b) Analitis Preskriptif: Kaedah analisis ini mensimulasikan keseluruhan rangkaian supaya, diberikan satu set pembolehubah dan kekangan yang perlu dipatuhi, daripada Tentukan penyelesaian terbaik atau boleh dilaksanakan di kalangan bilangan yang besar calon, biasanya dengan matlamat memaksimumkan matlamat perniagaan yang dinyatakan seperti daya pengeluaran, penggunaan, output, dsb. Masalah pengoptimuman ini digunakan secara meluas dalam bidang perancangan dan penjadualan rantaian bekalan, seperti apabila pembekal logistik mencipta jadual untuk sumbernya (kenderaan, kakitangan) untuk memaksimumkan penghantaran tepat pada masanya juga apabila pengilang membuat jadual; yang Optimumkan penggunaan mesin dan operator untuk mencapai penghantaran OTIF (On Time In Full) maksimum. Teknik sains data yang digunakan di sini ialah pengoptimuman matematik terhad, algoritma yang menggunakan penyelesai yang berkuasa untuk menyelesaikan masalah yang didorong oleh keputusan yang kompleks.

Ringkasnya, model ML meramalkan hasil yang mungkin untuk set ciri input tertentu berdasarkan data sejarah dan model pengoptimuman membantu anda membuat keputusan, jika hasil yang diramalkan berlaku, cara anda harus merancang untuk menyelesaikan/mengurangkan/mengeksploitasinya , kerana Perniagaan anda mempunyai beberapa matlamat yang berpotensi bersaing yang mungkin anda pilih untuk diteruskan dengan sumber yang terhad. Kedua-dua bidang sains data ini, sambil berkongsi beberapa alatan (seperti perpustakaan Python), menggerakkan saintis data dengan set kemahiran yang berbeza sama sekali - mereka sering memerlukan cara berfikir dan memodelkan masalah perniagaan yang berbeza. Jadi, mari kita cuba memahami dan membandingkan kaedah yang terlibat supaya saintis data yang berpengalaman dalam satu domain boleh memahami dan memanfaatkan kemahiran dan teknik silang yang mungkin boleh digunakan dalam domain lain.

Kes Aplikasi Berkembar Digital

Sebagai perbandingan, mari kita pertimbangkan model berkembar bagi proses analisis punca pengeluaran berasaskan ML (RCA: Analisis Punca Akar), yang tujuannya adalah untuk mendiagnosis produk siap atau Punca utama kecacatan atau anomali yang ditemui semasa pembuatan. Ini akan membantu pengurus jabatan menghapuskan punca yang paling berkemungkinan berdasarkan ramalan alat, akhirnya mengenal pasti isu dan melaksanakan CAPA (Tindakan Pembetulan & Pencegahan: tindakan pembetulan dan pencegahan), dan menyemak imbas semua rekod penyelenggaraan mesin dengan cepat dan tanpa menghabiskan banyak tenaga kerja , operator rekod sejarah, proses SOP (Standard Operating Procedure: Standard Operating Procedure), input sensor IoT, dsb. Matlamatnya adalah untuk meminimumkan masa henti mesin, kehilangan pengeluaran dan meningkatkan penggunaan sumber.

Secara teknikal, ini boleh dianggap sebagai masalah klasifikasi pelbagai kelas. Dalam masalah ini, dengan mengandaikan kecacatan tertentu wujud, model cuba meramalkan kebarangkalian setiap satu set kemungkinan label punca, seperti berkaitan mesin, berkaitan pengendali, berkaitan arahan proses, berkaitan bahan mentah, atau sesuatu yang lain , serta sebab terperinci seperti penentukuran mesin, penyelenggaraan mesin, kemahiran pengendali, latihan pengendali, dll. di bawah label pengelasan peringkat pertama ini. Walaupun penyelesaian optimum untuk situasi ini memerlukan penilaian beberapa model ML yang kompleks, untuk menekankan tujuan artikel ini, mari kita permudahkan sedikit - anggap ini adalah masalah regresi logistik multinomial (atas sebab yang akan menjadi jelas dalam bahagian seterusnya).

Sebagai perbandingan, mari kita pertimbangkan kembar yang dioptimumkan dalam proses perancangan pengeluaran, yang menjana jadual berdasarkan mesin, pengendali, langkah proses, tempoh, jadual ketibaan bahan mentah, tarikh akhir, dll. , percubaan untuk memaksimumkan objektif seperti output atau hasil. Garis masa automatik sedemikian membantu organisasi melaraskan sumber mereka dengan cepat untuk bertindak balas terhadap peluang baharu daripada pasaran (seperti permintaan terhadap ubat akibat COVID-19) atau untuk memaksimumkan kesan bahan mentah, pembekal, penyedia logistik dan campuran pelanggan/pasaran mereka. Kurangkan kesan peristiwa yang tidak dijangka, seperti kesesakan rantaian bekalan baru-baru ini.

Pada peringkat asas untuk memodelkan sebarang masalah perniagaan, membangunkan kembar digital sedemikian memerlukan pertimbangan yang berikut:

A ciri atau dimensi input

B. — Nilai dimensi ini

C, peraturan transformasi input kepada output

D, output atau sasaran

Seterusnya, mari analisa dan bandingkan pembelajaran mesin dengan lebih mendalam ( ML ) dan optimumkan faktor ini dalam model di bawah kekangan:

A. Ciri input: Ini adalah dimensi data dalam sistem, sesuai untuk ML dan pengoptimuman. Untuk model ML yang cuba mendiagnosis masalah dalam proses pengeluaran, ciri yang perlu dipertimbangkan mungkin termasuk: input IoT, data penyelenggaraan mesin sejarah, kemahiran operator dan maklumat latihan, maklumat kualiti bahan mentah, SOP yang diikuti (Prosedur Operasi Standard) dan kandungan lain .

Begitu juga, dalam persekitaran pengoptimuman yang terhad, ciri yang perlu dipertimbangkan termasuk: ketersediaan peralatan, ketersediaan operator, ketersediaan bahan mentah, waktu bekerja, produktiviti, kemahiran, dsb. yang biasanya diperlukan untuk membangunkan yang optimum ciri rancangan pengeluaran.

B. Data input: Di sinilah kedua-dua kaedah di atas menggunakan nilai eigen dalam cara yang berbeza. Antaranya, model ML memerlukan sejumlah besar data sejarah untuk latihan. Walau bagaimanapun, kerja penting yang berkaitan dengan penyediaan, pengurusan dan penormalan data sering diperlukan sebelum data boleh dimasukkan ke dalam model. Adalah penting untuk ambil perhatian bahawa sejarah ialah rekod peristiwa yang sebenarnya berlaku (seperti kegagalan mesin atau isu kemahiran pengendali yang mengakibatkan output tidak mencukupi), tetapi biasanya bukan gabungan mudah semua nilai yang mungkin ciri-ciri boleh diperolehi. Dalam erti kata lain, sejarah transaksi akan mengandungi lebih banyak rekod untuk senario yang kerap berlaku, manakala rekod yang agak sedikit untuk beberapa senario lain—mungkin kurang untuk senario yang jarang berlaku. Matlamat melatih model adalah untuk mempelajari hubungan antara ciri dan label output dan untuk meramalkan label yang tepat—walaupun terdapat sedikit atau tiada nilai ciri atau gabungan nilai ciri dalam data latihan.

Sebaliknya, untuk kaedah pengoptimuman, nilai ciri biasanya disimpan pada data sebenar mereka, cth., hari, kelompok, tarikh akhir, ketersediaan bahan mentah mengikut tarikh, jadual penyelenggaraan, masa pertukaran mesin, langkah proses , kemahiran pengendali, dsb. Perbezaan utama daripada model ML ialah pemprosesan data input memerlukan penjanaan jadual indeks untuk setiap kemungkinan gabungan yang sah bagi nilai ciri data induk (cth., hari, kemahiran, mesin, pengendali, jenis proses, dll.) untuk membentuk senarai bahagian penyelesaian yang boleh dilaksanakan. Sebagai contoh, pengendali A menggunakan mesin M1 pada hari pertama dalam minggu, melakukan langkah 1 proses pada tahap kemahiran S1, atau operator B menggunakan mesin M1 pada hari kedua, melaksanakan langkah 1 pada tahap kemahiran S2; walaupun untuk Setiap kemungkinan gabungan pengendali, mesin, tahap kemahiran, tarikh, dsb., tidak kira sama ada kombinasi tersebut benar-benar berlaku pada masa lalu. Ini menghasilkan set rekod data input yang sangat besar yang diberikan kepada enjin pengoptimuman. Matlamat model pengoptimuman adalah untuk memilih gabungan nilai eigen tertentu yang mematuhi kekangan yang diberikan sambil memaksimumkan (atau meminimumkan) persamaan objektif.

C. Peraturan penukaran input kepada output: Ini juga merupakan perbezaan ketara antara kedua-dua kaedah. Walaupun kedua-dua model ML dan pengoptimuman adalah berdasarkan teori matematik lanjutan, pemodelan matematik dan pengaturcaraan masalah perniagaan yang kompleks dalam kaedah pengoptimuman biasanya memerlukan lebih banyak usaha berbanding dengan ML, yang akan ditunjukkan dalam pengenalan berikut.

Alasannya ialah dalam ML, dengan bantuan perpustakaan sumber terbuka seperti scikit-learn, rangka kerja seperti Pytorch atau Tensorflow, dan juga model ML/pembelajaran mendalam daripada pembekal perkhidmatan awan, peraturan untuk menukar input kepada output boleh ditukar ganti sepenuhnya. Terpulang kepada model untuk mencari, yang juga termasuk tugas membetulkan kehilangan untuk memperoleh peraturan yang optimum (berat, berat sebelah, fungsi pengaktifan, dll.). Tanggungjawab utama seorang saintis data adalah untuk memastikan kualiti dan kesempurnaan ciri input dan nilainya.

Untuk kaedah pengoptimuman, ini tidak berlaku, kerana peraturan bagaimana input berinteraksi dan ditukar kepada output mesti ditulis dengan menggunakan persamaan terperinci dan kemudian disuapkan kepada penyelesai seperti Gurobi, CPLEX, dll. untuk mencari penyelesaian yang optimum atau mungkin. Tambahan pula, merumuskan masalah perniagaan sebagai persamaan matematik memerlukan pemahaman yang mendalam tentang saling hubungan dalam proses pemodelan dan memerlukan saintis data untuk bekerjasama rapat dengan penganalisis perniagaan.

Di bawah, mari kita gambarkan ini dengan gambar rajah skema model regresi logistik untuk aplikasi RCA (Analisis Punca Punca) masalah:

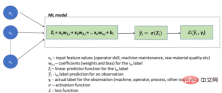
Logistik Regresi ML Model

Perhatikan bahawa dalam kes ini, tugas mengira peraturan (Zᵢ) untuk menjana hasil berdasarkan data input diserahkan kepada model untuk membuat kesimpulan, manakala saintis data biasanya sibuk menggunakan matriks kekeliruan yang jelas. , RMSE dan teknik pengukuran lain kepada pendekatan Visual untuk mencapai ramalan yang tepat.

Kita boleh membandingkannya dengan cara rancangan pengeluaran dijana melalui kaedah pengoptimuman:

(I) Langkah pertama ialah menentukan peraturan perniagaan (kekangan) yang merangkumi proses perancangan .

Berikut ialah contoh rancangan pengeluaran:

Pertama, kami mentakrifkan beberapa pembolehubah input (sesetengahnya boleh menjadi pembolehubah keputusan, digunakan untuk memacu matlamat):

• Bᵦ,_p,ᵢ——Pembolehubah binari, menunjukkan sama ada kelompok β (dalam jadual kelompok) produk p (dalam jadual produk) dijadualkan pada hari ke-i .
• Oₒ,_p,ᵢ – Pembolehubah binari yang menunjukkan sama ada operator pada indeks o (dalam jadual operator) dijadualkan untuk memproses kumpulan produk p pada hari i.
• M_m,_p,ᵢ - Pembolehubah binari yang menunjukkan sama ada mesin dengan indeks m (dalam jadual mesin) dijadualkan untuk memproses kumpulan pada hari i Produk hlm.

dan beberapa pekali:

• TOₒ,_p – masa yang diambil oleh operator o untuk memproses sekumpulan produk p.
• TM_m,_p——Masa yang diambil untuk mesin m memproses sekumpulan produk p.
• OAvₒ,ᵢ – Bilangan jam tersedia untuk indeks operator o pada hari i.
• MAv_m,ᵢ——Bilangan jam tersedia untuk mesin dengan indeks m pada hari i.

Dalam kes ini, beberapa kekangan (peraturan) boleh dilaksanakan menggunakan perkara berikut:

a) Dalam rancangan, kumpulan tertentu hanya boleh dimulakan sekali.

Di mana, untuk setiap kumpulan produk, Bt ialah jumlah bilangan kumpulan, Pr ialah jumlah bilangan produk, dan D ialah bilangan hari dalam pelan:

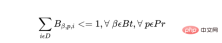
b) Satu produk hanya boleh dimulakan sekali sehari pada operator atau mesin.

Untuk setiap hari bagi setiap produk, di mana Op ialah set semua operator dan Mc ialah set semua mesin:

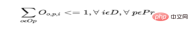
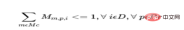
c) Jumlah masa yang dibelanjakan untuk satu kelompok (semua produk) tidak boleh melebihi waktu yang tersedia bagi operator dan mesin untuk hari tersebut.

Bagi setiap pengendali, terdapat kekangan berikut:

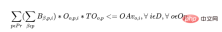
Untuk setiap mesin, untuk setiap hari, terdapat kekangan berikut:

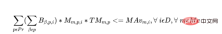
d) Jika pengendali memproses kumpulan produk dalam tempoh 5 hari pertama jadual, semua kumpulan lain produk yang sama mesti diperuntukkan kepada operator yang sama. Ini mengekalkan kesinambungan dan produktiviti pengendali.

Bagi setiap pengendali dan setiap produk, kekangan berikut wujud untuk setiap hari d (dari hari ke-6 dan seterusnya):

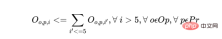
Perkara di atas diperlukan dalam program Beberapa daripada ratusan kekangan yang ditulis untuk membentuk peraturan perniagaan bagi senario penjadualan pengeluaran sebenar ke dalam persamaan matematik. Ambil perhatian bahawa kekangan ini ialah persamaan linear (atau, lebih khusus, persamaan integer bercampur). Walau bagaimanapun, perbezaan kerumitan antara mereka dan model ML regresi logistik masih sangat jelas.

(II) Setelah kekangan ditentukan, sasaran output perlu ditakrifkan. Ini adalah langkah kritikal dan boleh menjadi proses yang kompleks, seperti yang dijelaskan dalam bahagian seterusnya.

(III) Akhir sekali, pembolehubah keputusan input, kekangan dan objektif dihantar kepada penyelesai untuk mendapatkan penyelesaian (jadual).

Rajah skematik yang menerangkan kembar digital berdasarkan kaedah pengoptimuman adalah seperti berikut:

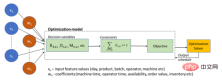
Model pengoptimuman

D, output atau Matlamat: Untuk model ML, bergantung pada jenis masalah (pengkelasan, regresi, pengelompokan), output dan metrik untuk mengukur ketepatannya boleh ditetapkan dengan baik. Walaupun saya tidak akan menyelidiki isu-isu ini dalam artikel ini, memandangkan banyak maklumat yang tersedia, perlu diperhatikan bahawa output pelbagai model boleh dinilai dengan tahap automasi yang tinggi, seperti CSP terkemuka (AWS Sagemaker, Azure ML, dsb.).

Menilai sama ada model yang dioptimumkan menjana output yang betul adalah lebih mencabar. Model pengoptimuman berfungsi dengan cuba memaksimumkan atau meminimumkan ungkapan pengiraan yang dipanggil "objektif." Seperti kekangan, bahagian matlamat direka oleh saintis data berdasarkan perkara yang cuba dicapai oleh perniagaan. Lebih khusus lagi, ini dicapai dengan melampirkan syarat ganjaran dan syarat penalti pada pembolehubah keputusan, jumlah yang cuba dimaksimumkan oleh pengoptimum. Untuk masalah dunia sebenar, ia memerlukan banyak lelaran untuk mencari pemberat yang betul untuk matlamat yang berbeza untuk mencari keseimbangan yang baik antara matlamat yang kadangkala bercanggah.

Untuk menggambarkan lebih lanjut contoh penjadualan pengeluaran di atas, kami juga boleh mereka bentuk dua matlamat berikut:

a) Jadual harus dimuatkan lebih awal; mungkin, dan baki kapasiti dalam pelan hendaklah berada di penghujung rancangan. Kita boleh melakukan ini dengan melampirkan penalti sehari pada kumpulan, yang akan meningkat secara beransur-ansur setiap hari dalam jadual.

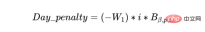
b) Sebaliknya, kami juga ingin mengelompokkan kumpulan produk yang sama supaya sumber (pengendali dan mesin) sebahagiannya digunakan secara optimum, dengan syarat kumpulan itu memenuhi tarikh akhir penghantaran dan kumpulan berada dalam satu operasi. tidak melebihi kapasiti mesin. Oleh itu, kami mentakrifkan Batch_group_bonus yang memberikan bonus yang lebih tinggi (oleh itu eksponen dalam ungkapan di bawah) jika kelompok disusun dalam kumpulan yang lebih besar dan bukannya dalam kumpulan yang lebih kecil. Adalah penting untuk ambil perhatian bahawa ini kadangkala boleh bersilang dengan sasaran sebelumnya, kerana beberapa kelompok yang mungkin bermula hari ini akan dimulakan dengan lebih banyak kelompok yang tersedia dalam beberapa hari, yang berpotensi meninggalkan beberapa sumber yang tidak dipenuhi pada awal jadual.

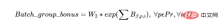
Bergantung pada cara penyelesai berfungsi, pelaksanaan sebenar selalunya memerlukan pembolehubah keputusan kumpulan kelompok. Walau bagaimanapun, ini menyatakan konsep berikut:

Penyelesai akan memaksimumkan objektif, iaitu:

objective=Batch_group_bonus+Day_penalty

Daripada dua komponen objektif di atas , yang manakah mempunyai kesan yang lebih besar pada hari tertentu jadual bergantung pada pemberat W₁, W₂ dan tarikh jadual, kerana pada peringkat akhir jadual, nilai penalti hari secara beransur-ansur akan menjadi lebih besar (semakin tinggi nilai i ). Jika nilai penalti hari lebih besar daripada bonus_kumpulan_Batch pada satu ketika, penyelesai perancangan akan mendapati adalah bijak untuk tidak menjadualkan kumpulan oleh itu, walaupun terdapat kapasiti sumber dalam pelan, penalti sifar akan dikenakan, dengan itu menjadualkan dan menanggung; penalti negatif bersih, dengan itu memaksimumkan matlamat. Isu ini perlu diselesaikan dan diselesaikan oleh saintis data.

Perbandingan beban kerja relatif antara kaedah ML dan kaedah pengoptimuman

Berdasarkan perbincangan di atas, boleh disimpulkan bahawa, secara amnya, projek pengoptimuman memerlukan lebih banyak usaha daripada projek ML. Pengoptimuman memerlukan kerja sains data yang meluas pada hampir setiap peringkat proses pembangunan. Ringkasan khusus adalah seperti berikut:

a) Pemprosesan data input : Dalam ML dan pengoptimuman, ini dilakukan oleh saintis data. Pemprosesan data ML memerlukan pemilihan ciri yang berkaitan, penyeragaman, pendiskretan, dsb. Untuk data tidak berstruktur seperti teks, ia boleh termasuk kaedah berasaskan NLP seperti pengekstrakan ciri, tokenisasi, dsb. Pada masa ini, perpustakaan berdasarkan pelbagai bahasa wujud untuk analisis statistik ciri serta kaedah pengurangan dimensi seperti PCA.

Dalam pengoptimuman, setiap perniagaan dan rancangan mempunyai nuansa yang perlu dimasukkan ke dalam model. Masalah pengoptimuman tidak berurusan dengan data sejarah, sebaliknya menggabungkan setiap perubahan data yang mungkin dan ciri yang dikenal pasti ke dalam indeks yang pembolehubah keputusan dan kekangan mesti bergantung. Walaupun tidak seperti ML, pemprosesan data memerlukan banyak kerja pembangunan.

b) Pembangunan model : Seperti yang dinyatakan di atas, perumusan model penyelesaian pengoptimuman memerlukan banyak usaha daripada saintis data dan penganalisis perniagaan untuk merumuskan kekangan dan matlamat. Penyelesai menjalankan algoritma matematik, dan walaupun ia ditugaskan untuk menyelesaikan ratusan atau bahkan ribuan persamaan serentak untuk mencari penyelesaian, ia tidak mempunyai latar belakang perniagaan.

Dalam ML, latihan model sangat automatik dan algoritma dibungkus sebagai API perpustakaan sumber terbuka atau dibungkus oleh penyedia perkhidmatan awan. Model rangkaian saraf pra-latihan yang sangat kompleks berdasarkan data khusus perniagaan memudahkan tugas latihan sehingga beberapa lapisan terakhir. Alat seperti AWS Sagemaker Autopilot atau Azure AutoML malah boleh mengautomasikan keseluruhan proses pemprosesan data input, pemilihan ciri, latihan dan penilaian model dan penjanaan output yang berbeza.

c) Pengujian dan pemprosesan output : Dalam ML, output model boleh dimanfaatkan dengan pemprosesan yang minimum. Ia umumnya mudah difahami (cth., kebarangkalian label yang berbeza), walaupun beberapa usaha mungkin diperlukan untuk memperkenalkan aspek lain, seperti kebolehtafsiran keputusan. Visualisasi output dan ralat juga mungkin memerlukan sedikit usaha, tetapi ia tidak banyak berbanding dengan pemprosesan input.

Di sini juga, masalah pengoptimuman memerlukan ujian dan pengesahan manual berulang dengan mata terlatih pakar perancangan untuk menilai kemajuan. Walaupun penyelesai cuba untuk memaksimumkan objektif, ini dengan sendirinya sering tidak masuk akal dari perspektif kualiti jadual. Tidak seperti ML, seseorang tidak boleh mengatakan bahawa nilai sasaran di atas atau di bawah ambang mengandungi pelan yang betul atau salah. Apabila jadual didapati tidak konsisten dengan objektif perniagaan, masalah mungkin berkaitan dengan kekangan, pembolehubah keputusan atau fungsi objektif dan memerlukan analisis yang teliti untuk mencari punca anomali dalam jadual yang besar dan kompleks.

Selain itu, sesuatu yang perlu dipertimbangkan ialah pembangunan yang diperlukan untuk mentafsir output penyelesai ke dalam format yang boleh dibaca manusia. Penyelesai mengambil pembolehubah keputusan input, iaitu nilai indeks entiti fizikal sebenar dalam pelan, seperti indeks kumpulan kelompok, indeks keutamaan kelompok, indeks pengendali dan mesin, dan mengembalikan nilai yang dipilih. Pemprosesan terbalik diperlukan untuk menukar nilai indeks ini daripada bingkai data masing-masing kepada garis masa yang koheren yang boleh dipersembahkan dan dianalisis secara visual oleh pakar.

d) Akhirnya, walaupun dalam fasa operasi, model ML memerlukan lebih sedikit pengiraan dan masa untuk menjana ramalan pemerhatian berbanding fasa latihan. Walau bagaimanapun, jadual dibina dari awal setiap kali dan memerlukan sumber yang sama untuk setiap larian.

Angka berikut ialah ilustrasi kasar beban kerja relatif bagi setiap peringkat ML dan projek pengoptimuman:

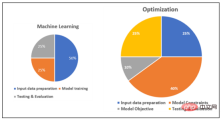
Gambarajah skematik membandingkan beban kerja relatif ML dan pengoptimuman

Bolehkah ML dan pengoptimuman berfungsi bersama?

Pembelajaran dan pengoptimuman mesin menyelesaikan masalah pelengkap untuk perusahaan, oleh itu, output model ML dan pengoptimuman menguatkan satu sama lain, dan sebaliknya. Aplikasi AI/ML seperti penyelenggaraan ramalan IoT dan pengesanan kerosakan, penyelenggaraan jauh AR/VR dan proses pengeluaran RCA yang dinyatakan di atas merupakan sebahagian daripada strategi kilang yang disambungkan oleh pengeluar.

Aplikasi pengoptimuman membentuk asas perancangan rantaian bekalan dan boleh dianggap sebagai menghubungkan strategi perniagaan kepada operasi. Mereka membantu organisasi bertindak balas dan merancang untuk kejadian yang tidak dijangka. Contohnya, jika masalah dikesan dalam barisan pengeluaran, alat RCA (Analisis Punca Akar) akan membantu pengurus barisan pengeluaran dengan cepat mengecilkan kemungkinan punca dan mengambil tindakan yang perlu. Walau bagaimanapun, ini kadangkala boleh menyebabkan penutupan mesin yang tidak dijangka atau penugasan semula arahan pengendalian. Oleh itu, rancangan pengeluaran mungkin perlu dijana semula menggunakan kapasiti berkurangan yang tersedia.

Sesetengah teknik ML boleh digunakan untuk pengoptimuman, dan begitu juga sebaliknya?

Pengalaman daripada projek ML boleh digunakan untuk projek pengoptimuman dan sebaliknya. Sebagai contoh, untuk fungsi objektif yang penting untuk mengoptimumkan output, kadangkala unit perniagaan tidak ditakrifkan dengan baik dari segi pemodelan matematik seperti kekangan, yang merupakan peraturan yang mesti dipatuhi dan oleh itu biasanya terkenal. Sebagai contoh, objektif perniagaan adalah seperti berikut:

a) Kelompok harus diutamakan seawal mungkin sambil mematuhi tarikh akhir penghantaran.

b) Jadual hendaklah dimuatkan terlebih dahulu; hendaklah dijadualkan dengan selang sekecil mungkin dan dengan penggunaan sumber yang rendah.

c) Kelompok hendaklah dikumpulkan untuk menggunakan kapasiti dengan cekap.

d) Operator yang mempunyai tahap kemahiran yang lebih tinggi untuk produk bernilai tinggi adalah yang terbaik diberikan kumpulan sedemikian.

Sesetengah daripada matlamat ini mungkin mempunyai keutamaan bersaing yang perlu diseimbangkan dengan betul, yang menyebabkan saintis data apabila menulis kombinasi kompleks faktor yang mempengaruhi (seperti bonus dan denda) sering mengikut perkara yang paling sesuai senario perancangan biasa dicapai melalui percubaan dan kesilapan; tetapi kadangkala apabila kelemahan timbul, logiknya sukar untuk difahami dan dikekalkan. Oleh kerana penyelesai pengoptimuman sering menggunakan produk pihak ketiga, kod mereka selalunya tidak tersedia kepada saintis data yang membina model yang mereka mahu nyahpepijat. Ini menjadikannya mustahil untuk melihat nilai bonus dan penalti tertentu yang diambil pada mana-mana titik tertentu dalam proses penjanaan jadual, dan nilai inilah yang menjadikannya berkelakuan dengan betul, yang menjadikan penulisan ungkapan sasaran yang meyakinkan sangat penting.

Oleh itu, pendekatan di atas membantu untuk menerima pakai penyeragaman bonus dan penalti, yang merupakan amalan ML yang digunakan secara meluas. Nilai yang dinormalkan kemudiannya boleh diskalakan secara terkawal menggunakan parameter konfigurasi atau cara lain untuk mengawal kesan setiap faktor, hubungannya antara satu sama lain, dan nilai faktor sebelumnya dan berikut dalam setiap faktor tersebut.

Kesimpulan

Ringkasnya, pembelajaran mesin dan pengoptimuman terhad adalah kedua-dua kaedah matematik lanjutan untuk menyelesaikan masalah yang berbeza dalam organisasi dan kehidupan harian. Kesemuanya boleh digunakan untuk menggunakan kembar digital peralatan fizikal, proses atau sumber rangkaian. Walaupun kedua-dua jenis aplikasi mengikuti proses pembangunan peringkat tinggi yang serupa, projek ML boleh memanfaatkan tahap automasi tinggi yang tersedia dalam perpustakaan dan algoritma asli awan, manakala pengoptimuman memerlukan kerjasama rapat antara ahli perniagaan dan saintis data untuk melaksanakan sepenuhnya proses perancangan yang kompleks pemodelan. Secara umumnya, projek pengoptimuman memerlukan lebih banyak kerja pembangunan dan intensif sumber. Dalam pembangunan sebenar, ML dan alat pengoptimuman selalunya perlu bekerjasama dalam perusahaan, dan kedua-dua teknologi berguna untuk saintis data.

Pengenalan penterjemah

Zhu Xianzhong, editor komuniti 51CTO, blogger pakar 51CTO, pensyarah, guru komputer di sebuah universiti di Weifang dan seorang veteran dalam industri pengaturcaraan bebas.

Tajuk asal: ​​Pemodelan Berkembar Digital Menggunakan Pembelajaran Mesin dan Pengoptimuman Terkandas​​, pengarang: Partha Sarkar

Atas ialah kandungan terperinci Pemodelan kembar digital berdasarkan pembelajaran mesin dan pengoptimuman terhad. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!