Bagaimana untuk melaksanakan pengisihan mudah di Jawa

Pengisihan adalah operasi yang sangat biasa dan teras dalam pemprosesan data Walaupun dalam pembangunan projek sebenar, terdapat kemungkinan kecil bahawa kami perlu melaksanakannya secara manual. terdapat perpustakaan kelas dalam setiap bahasa Terdapat banyak pelaksanaan algoritma pengisihan. Tetapi ia masih memberi manfaat besar kepada kita untuk memahami idea-idea halus ini. Artikel ini mengkaji secara ringkas tiga jenis algoritma yang paling asas: pemilihan, menggelegak dan sisipan.

Mula-mula tentukan fungsi untuk menukar elemen tatasusunan, yang boleh dipanggil semasa mengisih

/**
     * 交换数组元素
     * @param arr
     * @param a
     * @param b
     */
    public static void swap(int []arr,int a,int b){
        arr[a] = arr[a]+arr[b];
        arr[b] = arr[a]-arr[b];
        arr[a] = arr[a]-arr[b];
    }

Isih pemilihan mudah

Isih pemilihan mudah ialah algoritma yang paling mudah dan intuitif. Ideanya adalah untuk memilih elemen terkecil (atau terbesar) daripada elemen data untuk diisih sebagai elemen pertama untuk setiap laluan sehingga semua elemen diisih Pengisihan pemilihan mudah ialah pengisihan yang tidak stabil.

Apabila algoritma dilaksanakan, setiap kali elemen minimum ditentukan, kedudukan pertama akan menjadi minimum semasa melalui perbandingan berterusan dan pertukaran adalah operasi yang agak memakan masa. Malah, kita boleh dengan mudah mendapati bahawa pertukaran ini tidak bermakna sebelum elemen minimum semasa ditentukan sepenuhnya. Kita boleh menetapkan min pembolehubah untuk menyimpan hanya subskrip tatasusunan elemen yang lebih kecil untuk setiap perbandingan Apabila gelung berakhir, pembolehubah ini menyimpan subskrip elemen terkecil semasa, dan kemudian melaksanakan operasi pertukaran. Pelaksanaan kod adalah sangat mudah, mari kita lihat.

Pelaksanaan kod

/**
     * 简单选择排序
     *
     * @param arr
     */
    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int min = i;//每一趟循环比较时，min用于存放较小元素的数组下标，这样当前批次比较完毕最终存放的就是此趟内最小的元素的下标，避免每次遇到较小元素都要进行交换。
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    min = j;
                }
            }
            //进行交换，如果min发生变化，则进行交换
            if (min != i) {
                swap(arr,min,i);
            }
        }
    }

Selepas pengisihan pemilihan mudah dioptimumkan di atas, bilangan perbandingan kekal tidak berubah tanpa mengira susunan asal tatasusunan untuk operasi pertukaran, dalam kes terbaik, ia ialah tatasusunan Apabila ia dipesan sepenuhnya, tiada pertukaran pertukaran diperlukan Dalam kes yang paling teruk, iaitu, apabila tatasusunan dalam susunan terbalik, bilangan pertukaran ialah n-1. Secara keseluruhannya, kerumitan masa ialah O(n2)

Isih gelembung

Idea asas isihan gelembung ialah membandingkan unsur-unsur bersebelahan secara berpasangan, dan menukarnya jika susunannya diterbalikkan dengan cara ini, setiap pas akan "mengapungkan" elemen terkecil atau terbesar ke atas, dan akhirnya mencapai susunan lengkap

Pelaksanaan kod

dalam isihan gelembung Semasa proses, jika perjalanan tertentu selesai tanpa sebarang operasi pertukaran, sebagai contoh, tatasusunan [5,4,1,2,3] melakukan menggelegak dua kali, iaitu, selepas dua gelung luar, 5 dan 4 dilaraskan kepada akhir kedudukan [1,2,3,4,5]. Pada masa ini, selepas melaksanakan gelung ketiga, tiada satu pertukaran telah dilakukan, yang bermaksud bahawa urutan yang tinggal sudah teratur, dan operasi pengisihan boleh diselesaikan Mari kita lihat kod

/**
     * 冒泡排序
     *
     * @param arr
     */
    public static void bubbleSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            boolean flag = true;//设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已然完成。
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    swap(arr,j,j+1);
                    flag = false;
                }
            }
            if (flag) {
                break;
            }
        }
    }

Mengikut pelaksanaan gelembung di atas, jika tatasusunan asal itu sendiri dipesan (ini adalah kes terbaik), hanya perbandingan n-1 boleh diselesaikan jika ia dalam susunan terbalik, bilangan perbandingan ialah n-1+ n-2+ ..+1=n(n-1)/2, bilangan pertukaran dan bilangan perbandingan adalah sama. Oleh itu, kerumitan masanya masih O(n2). Secara keseluruhannya, prestasi isihan gelembung masih lebih buruk sedikit daripada jenis pemilihan di atas.

Isih sisipan langsung

Idea asas isihan sisipan langsung ialah memasukkan rekod untuk diisih ke dalam urutan yang telah diisih sebelum ini pada setiap langkah sehingga semua elemen telah dimasukkan.

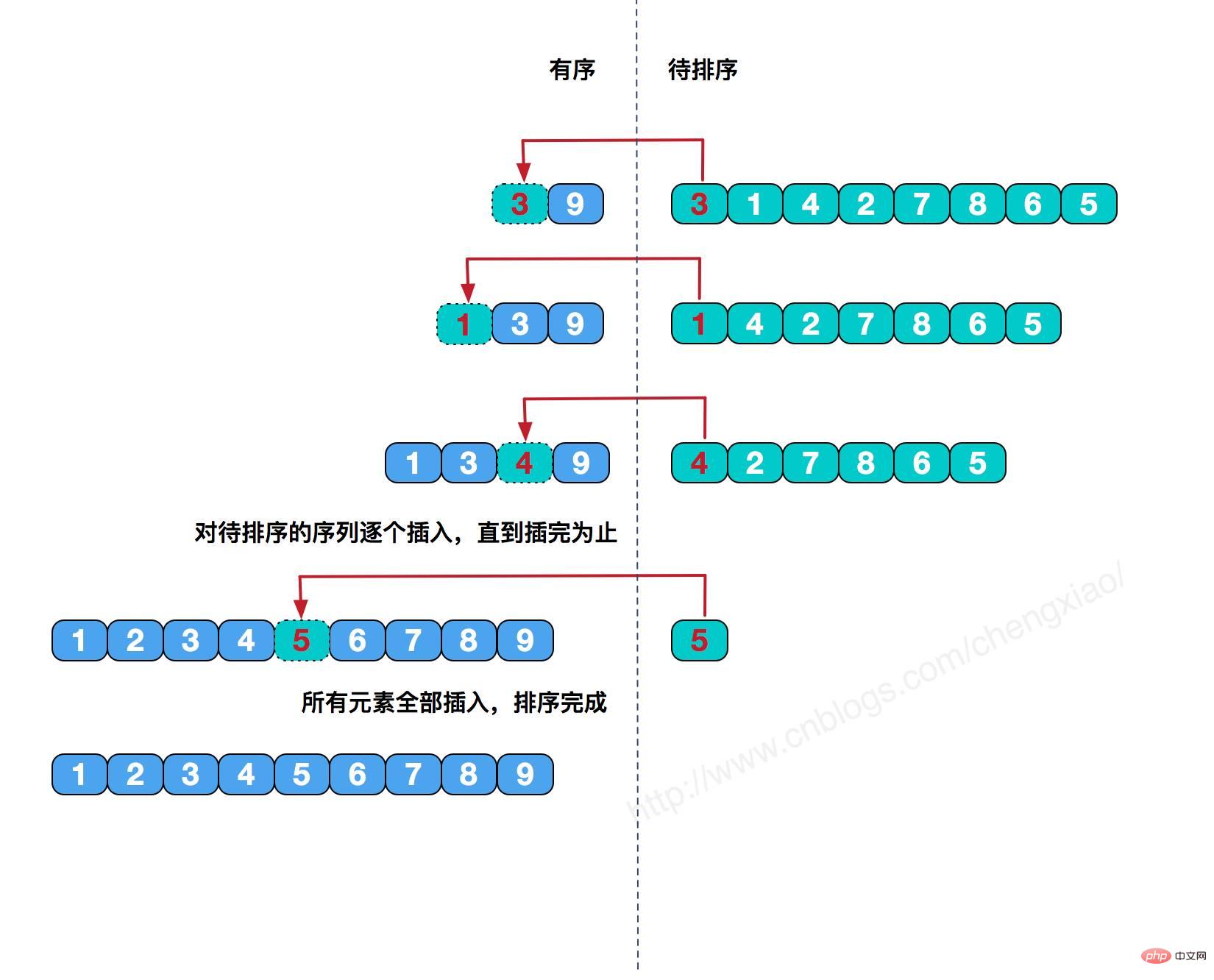
Pelaksanaan kod

/**
     * 插入排序
     *
     * @param arr
     */
    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int j = i;
            while (j > 0 && arr[j] < arr[j - 1]) {
                swap(arr,j,j-1);
                j--;
            }
        }
    }

Isihan sisipan mudah Dalam kes terbaik, ia perlu dibandingkan n-1 kali tanpa bertukar elemen dan masa kerumitan ialah O(n); dalam kes yang paling teruk, kerumitan masa masih O(n2). Tetapi apabila elemen tatasusunan disusun secara rawak, isihan sisipan masih lebih baik daripada dua jenis di atas.

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan pengisihan mudah di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!