Rumah >Peranti teknologi >AI >Mesin Turing: Bagaimanakah kita boleh bercakap tentang pengkomputeran tanpa ketiadaan komputer?
Mesin Turing: Bagaimanakah kita boleh bercakap tentang pengkomputeran tanpa ketiadaan komputer?
- PHPzke hadapan
- 2023-04-16 14:34:031549semak imbas
Pada Oktober 1950, kertas kerja bertajuk "Can Machines Think" telah diterbitkan. Makalah ini mencadangkan ujian yang mengerikan, di mana penguji dipisahkan daripada orang yang diuji (orang sebenar dan mesin) dengan bertanya soalan secara rawak kepada orang yang diuji melalui peranti komunikasi, dan meminta mereka kepada Penguji meneka sama ada orang yang mereka yang bercakap dengannya ialah orang sebenar atau mesin.
Selepas beberapa ujian, jika mesin boleh membuat setiap peserta membuat lebih daripada 30% salah penilaian secara purata, maka mesin itu telah lulus ujian dan dianggap seperti manusia.
Ini adalah ketika orang mula-mula menyedari bahawa robot mungkin memiliki kecerdasan manusia. Ujian ini ialah ujian Turing yang diperkatakan oleh jutaan peminat fiksyen sains. Artikel ini juga memenangi gelaran pengarang Alan Turing sebagai "Bapa Kepintaran Buatan".
Jalan menuju kecerdasan buatan, atau asal usul sejarah pembangunan komputer, ialah kertas kerja yang diterbitkan oleh Turing ketika berusia 24 tahun. Dalam makalah ini, beliau memberikan definisi matematik yang ketat kepada "kebolehhitungan" dan mencadangkan idea "Mesin Turing" yang terkenal. Mesin Turing bukanlah mesin khusus, tetapi model mental yang boleh mencipta peranti pengkomputeran yang sangat mudah tetapi sangat berkuasa yang boleh digunakan untuk mengira semua fungsi boleh dibayangkan.
Oleh kerana Turing mencipta mesin Turing, dari semasa ke semasa seseorang melompat keluar dan mendakwa bahawa Turing sebenarnya "mencipta komputer." Walau bagaimanapun, mesin Turing tidak direka bentuk dengan cara yang sama seperti mesin pengkomputeran sebenar. Mesin Turing bukanlah model abstrak mesin. Ternyata (seperti yang dibuktikan oleh kenyataan Turing) bahawa mesin Turing adalah model seseorang yang menulis di atas kertas di atas meja. Jadi, kenapa Turing mencipta mesin Turing, dan ke manakah mesin Turing akan membawa kita?
1 Kertas Turing “On Computable Numbers”
Cara terbaik untuk menjawab soalan ini ialah meletakkan buku teks di tepi dan membukanya. Hari ini, meminjam majalah 1936 tidak memerlukan mengisi kad pinjaman atau menunggu sejam untuk pustakawan mengambilnya dari perpustakaan Apa yang kami perlukan hanyalah segelas wiski malt di tangan dan akses mudah kepada Google di rumah. Kertas Turing yang kami cari adalah seperti berikut:

Alamat kertas: https://www.cs.virginia.edu/ ~robins/Turing_Paper_1936.pdf
Terdapat beberapa ralat dalam kertas tersebut, tetapi kelemahannya tidak diatasi. Seperti kata Joel David Hamkins, Turing mentakrifkan nombor nyata boleh dikira sebagai nombor dengan pengembangan perpuluhan boleh dikira, yang sebenarnya tidak berfungsi, tetapi ia tidak sukar untuk dibetulkan.
Turing menjelaskan niat menulis kertas ini dalam tajuk: "Mengenai nombor yang boleh dikira dan aplikasinya dalam "masalah keputusan". Antaranya, "Entscheidungsproblem (masalah keputusan) )" bertanya sama ada terdapat teknik yang cekap untuk memutuskan bahawa formula logik peringkat pertama adalah sah, iaitu, benar pada semua tafsiran
Turing membentangkan ideanya seperti berikut:.
Kita boleh membandingkan seseorang yang mengira nombor nyata dengan mesin yang hanya boleh memenuhi bilangan syarat yang terhad q1, q2,... qR... Terdapat satu dalam mesin ini "pita kertas" panjang melaluinya, dan pita kertas dibahagikan kepada banyak bahagian Kami memanggil kepingan ini segi empat sama, dan setiap segi empat sama boleh membawa "simbol"... ada yang menuliskan Simbol-simbol itu membentuk urutan digit perpuluhan yang sebenar. nombor sedang dikira, manakala simbol lain hanyalah nota kasar yang boleh dipadamkan pada pita Kaedah operasi meleret ke belakang dan ke belakang ke simbol tertentu dan memproses simbol dengan sewajarnya, termasuk semua operasi yang digunakan untuk pengiraan berangka "nombor boleh dikira" hanya bermaksud nombor nyata yang ungkapan perpuluhannya boleh dikira dengan cara terhad Menurut definisi saya, jika ungkapan perpuluhan nombor boleh ditulis oleh mesin, maka Nombor ini boleh dikira
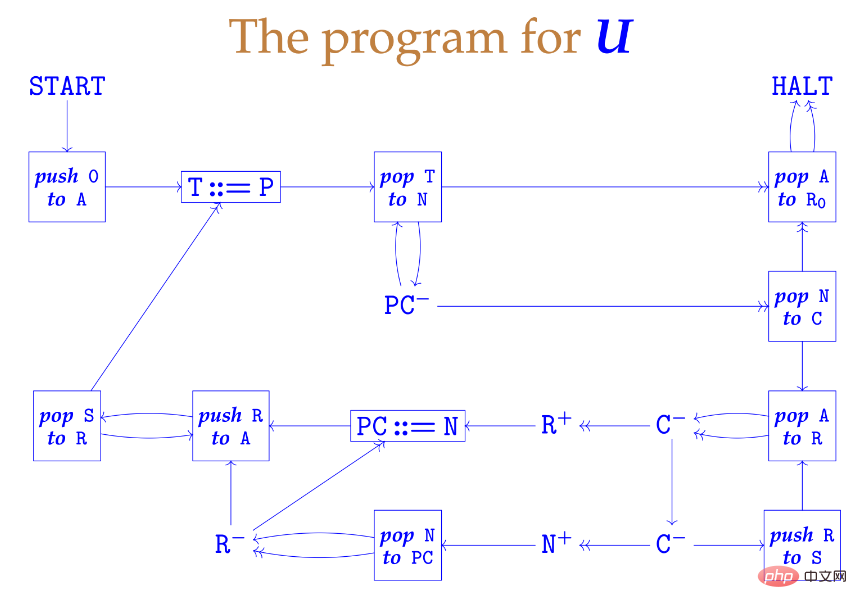
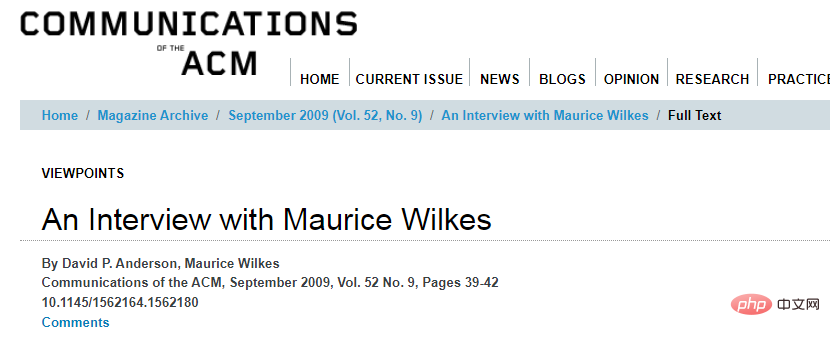
Turing kemudiannya mentakrifkan dan membuktikannya. Ini adalah kertas matematik biasa, bukan kertas kejuruteraan biasa Dalam artikel jenis ini, pembaca ingin mengetahui cara melaksanakan sesuatu Mekanisme yang diterangkan dalam artikel Dari tajuk dan artikel Turing kita dapat melihat bahawa Turing terutamanya berkaitan dengan pengiraan nombor nyata hingga tempat perpuluhan tak terhingga. Kertas kerja ini mempunyai banyak sumbangan penting lain: Selepas menulis kertas ini, Turing membuka sains pengkomputeran teori. pintu masuk ke padang. Kami tidak pasti apa yang memberi Turing idea tentang Mesin Turing Universal (UTM), tetapi sekali Jika difikirkan, dia mungkin berfikir bahawa kewujudan mesin Turing universal adalah jelas. Memandangkan tujuan mesin Turing adalah untuk mensimulasikan kerani yang bekerja di meja, dan pengendalian mesin Turing adalah sama seperti kerani—melakukan operasi ini atau itu mengikut senarai peraturan transformasi yang diberikan berdasarkan mesin simbol keadaan dan pita—sudah jelas mesin Turing diperlukan untuk melaksanakan tugas rutin tersebut. Kertas Turing adalah sedikit lakaran pada butiran pembinaan, tetapi tiada siapa yang peduli. Kini, kami mempunyai mesin Turing universal yang telah direka secara tajam dan jelas. Beberapa dekad yang lalu, di Universiti Cambridge, Dr. Ken Moody menulis keygen Minsky universal: Pautan: http: //www.igblan .free-online.co.uk/igblan/ca/minsky.html Mesin sedemikian mempunyai daftar terhad, setiap daftar boleh menyimpan sebarang integer bukan negatif Besar. Ia mempunyai program terhingga yang terdiri daripada tiga jenis arahan berlabel yang berbeza: Mesin sedemikian lebih mudah untuk diprogramkan berbanding mesin Turing, walaupun ia masih tidak kelihatan seperti komputer sebenar. Moody menggunakan bijection standard antara N dan N×N untuk mengemas senarai integer menjadi satu integer. Dia menulis perpustakaan kecil mesin daftar kecil yang melakukan operasi seperti menolak ke atas dan keluar dari timbunan, dan mencipta reka bentuk yang mengingatkan kitaran pengambilan-pelaksanaan pemproses sebenar. Keseluruhan proses boleh dilihat dalam slaid berikut. Gambar di bawah ialah mesin itu sendiri: Gambar di bawah ialah struktur keseluruhan mesin. (Pengarang kedua-dua gambar ini ialah Andrew Pitts, profesor sains pengkomputeran teori di Universiti Cambridge.) Anehnya, struktur ini mesin sangat mudah! Masalah terhenti jelas tidak dapat diputuskan. Jika tidak, banyak tekaan matematik sukar untuk diselesaikan, seperti Teorem Terakhir Fermat: Tulis sahaja atur cara yang mencari x, y, z, n>2, supaya Bertentangan dengan kepercayaan popular, kertas kerja Turing tidak membincangkan masalah terhenti, tetapi membincangkan ciri yang berkaitan dengan masalah terhenti, yang dipanggilnya "circularity". Mesin Turing adalah kitaran jika ia "menulis hanya bilangan terhad bagi simbol pertama" (iaitu 0s dan 1s). Saya fikir sebab kitaran penting ialah Turing sangat gemar menganggarkan nombor nyata sebagai rentetan binari tak terhingga. Ahli fizik Christopher Strachey mendakwa dalam surat 1965 kepada Jurnal Komputer bahawa Turing memberitahunya bukti ketidakpastian masalah terhenti. Pada September 2009, David P. Anderson menemu bual Maurice Wilkes, dan pandangannya tentang Turing adalah bertentangan dengan orang ramai: David P. Anderson: Pada pendapat anda, apakah kepentingan kertas kerja Turing 1936 mengenai masalah keputusan? Maurice Wilkes: Saya rasa seorang jurutera akan melihat idea program yang disimpan sebagai sejenis teori triniti yang penting dan berkata, "Ini benar-benar terkemuka. Ini adalah bagaimana ia harus dilakukan." Tiada perbezaan praktikal antara idea dalam kertas itu dan apa yang saya katakan. Dia bertuah kerana kertas itu diterbitkan, maksud saya Gereja Alonzo mendapat keputusan yang sama menggunakan kaedah lain. Alamat artikel: https://cacm.acm.org/magazines/2009/9/38898-an-interview-with -maurice-wilkes/fulltext Perlu diingatkan bahawa pada masa temu bual, Maurice Wilkes berumur 96 tahun Dia sendiri adalah perintis komputer terkenal, EDSAC (. Bapa Elektronik Kalkulator Automatik Storan Kelewatan, kalkulator automatik storan kelewatan elektronik. Dalam jawapannya yang pelik, seseorang dapat melihat rasa cemburunya terhadap status tinggi Turing. Mereka berdua jelas tidak serasi! Kami juga melihat penghinaan Maurice Wilkes terhadap teori: walaupun pengekodan mesin kepada nombor dijangka daripada komputer atur cara yang disimpan, kerja Turing adalah matematik tulen dan tidak mempunyai kepentingan kejuruteraan. Turing berminat dalam kejuruteraan komputer sebenar, tetapi banyak percubaannya untuk mengambil bahagian dalam projek sebenar telah dikecewakan. Dan apakah pendapat anda tentang komen tersebut tentang Gereja? Semasa Turing membuat penyelidikan, ramai penyelidik tertumpu pada idea "kebolehkiraan yang berkesan". Di sini saya mengesyorkan pembaca membaca "Masalah Tidak Boleh Selesaikan dalam Teori Nombor Asas" oleh Qiu Qi (lihat gambar di bawah). Pautan kertas: https://www.jstor.org/stable/2371045?origin=crossref Sejujurnya, kertas ini sukar dibaca, tetapi ia boleh membawa kita ke tempat kejadian. Artikel ini memberikan definisi λ-calculus, definisi fungsi rekursif (dalam pengertian Kleene/Gödel), dan beberapa soalan yang tidak dapat dipertikaikan tentang kewujudan dan kesetaraan paradigma dalam hasil Penghakiman. Church dan Craney telah membuktikan kesetaraan antara fungsi yang boleh ditentukan lambda dan fungsi rekursif dan semasa Turing berada di Princeton, kesetaraan antara fungsi boleh ditentukan lambda dan fungsi boleh dikira Turing juga telah dibuktikan , jadi kami mendapat tesis Church-Turing, yang mana merujuk kepada fakta bahawa fungsi boleh dikira secara berkesan adalah tepat fungsi tersebut dalam kelas kesetaraan matematik. Seperti yang sering orang katakan, kami tidak dapat membuktikan sama ada tesis ini betul atau tidak, kerana "boleh dikira secara berkesan" bukanlah konsep yang tepat. Kita boleh menganggap fungsi boleh dikira Turing sebagai kelas yang agak inklusif, kerana ia merangkumi banyak fungsi yang tidak boleh dikira dalam jangka hayat alam semesta. Dengan bantuan fungsi Ackermann, kita boleh mendapatkan contoh dengan mudah. Bentuk moden bagi fungsi Ackermann adalah seperti berikut: Pautan artikel: https:// lawrencecpaulson.github.io/2022/02/09/Ackermann-example.html Jika anda mentakrifkan f(n)=A(n,n) , anda tidak boleh mengharapkan Kira nombor genap f(4). g(n)=A(4,n), walaupun rekursi primitif, hampir mustahil untuk dikira. Walaupun tiada komputer digital sehingga tahun 1930-an, konsep kebolehkiraan yang cekap telah diketahui oleh ahli matematik. Konsep kesahan telah lama muncul dalam struktur garis lurus dan struktur kompas geometri Yunani Kesahan juga merupakan sebahagian daripada masalah keputusan dan masalah kesepuluh Hilbert. Kejeniusan konsep Turing, berbanding dengan fungsi rekursif Gödel dan kalkulus lambda Gereja, ialah ia jelas betul. Gödel sendiri tidak pasti sama ada fungsi rekursifnya menangkap idea pengiraan, dan kami tidak tahu sama ada idea Gereja itu betul. Hanya idea Turing yang mudah dan semula jadi. Idea Turing terbukti setara dengan model lain dan memberikan penjelasan yang munasabah untuk kesemuanya. Beliau menunjukkan fakta ini dalam kertas kerjanya pada tahun 1937 "Kebolehkomputasi dan Kebolehdefinan Lambda". Artikel ini bertujuan untuk membuktikan bahawa fungsi boleh dikira yang dicadangkan oleh pengarang adalah konsisten dengan fungsi λ-definable Gereja dan yang dicadangkan oleh Elbron and Co. fungsi rekursif am yang dicadangkan oleh Del dan dibangunkan oleh Kleiny adalah sama. Fungsi yang sama ini membuktikan bahawa setiap fungsi yang ditakrifkan X boleh dikira, dan setiap fungsi yang boleh dikira secara amnya adalah rekursif. Perhatikan bahawa Turing menulis "boleh dikira", tetapi kita perlu menulis "boleh dikira Turing".
2 Mesin Turing Universal


3 Masalah terhenti
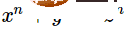 , dan tanya sama ada ia tamat. Walau bagaimanapun, ketidakpastian untuk berhenti mesti dinyatakan dan dibuktikan dengan teliti.
, dan tanya sama ada ia tamat. Walau bagaimanapun, ketidakpastian untuk berhenti mesti dinyatakan dan dibuktikan dengan teliti.
4 Turing dan Maurice Wilkes
5 Turing dan Gereja di Princeton

6 Adakah tesis Church-Turing betul?
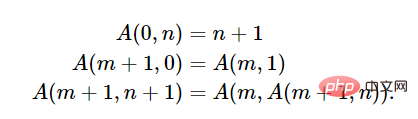
Atas ialah kandungan terperinci Mesin Turing: Bagaimanakah kita boleh bercakap tentang pengkomputeran tanpa ketiadaan komputer?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

