Lima fungsi kehilangan yang biasa digunakan untuk melatih rangkaian saraf pembelajaran mendalam

Pengoptimuman rangkaian saraf semasa latihan adalah untuk menganggarkan ralat keadaan semasa model dahulu, dan kemudian untuk mengurangkan ralat penilaian seterusnya, adalah perlu untuk mengemas kini pemberat menggunakan fungsi yang boleh mewakili ralat. Fungsi ini dipanggil fungsi kehilangan.

Pilihan fungsi kehilangan berkaitan dengan masalah pemodelan ramalan khusus (seperti pengelasan atau regresi) yang model rangkaian saraf belajar daripada contoh. Dalam artikel ini kami akan memperkenalkan beberapa fungsi kehilangan yang biasa digunakan, termasuk:

• Min kuadrat kehilangan ralat model regresi
• Entropi silang dan kehilangan engsel model klasifikasi binari

Fungsi kehilangan model regresi

Model ramalan regresi digunakan terutamanya untuk meramal nilai berterusan. Jadi kami akan menggunakan fungsi make_regression() scikit-learn untuk menjana beberapa data simulasi dan menggunakan data ini untuk membina model regresi.

Kami akan menjana 20 ciri input: 10 daripadanya akan bermakna, tetapi 10 akan tidak berkaitan dengan masalah itu.

Dan jana 1,000 contoh secara rawak. Dan tentukan benih rawak, jadi 1,000 contoh yang sama dijana setiap kali anda menjalankan kod.

Menskalakan pembolehubah input dan output bernilai sebenar kepada julat yang munasabah selalunya boleh meningkatkan prestasi rangkaian saraf. Jadi kita perlu menyeragamkan data.

StandardScaler juga boleh didapati dalam perpustakaan scikit-learn, untuk memudahkan masalah kami akan menskalakan semua data sebelum membahagikannya kepada set latihan dan ujian.

Kemudian bahagikan set latihan dan pengesahan sama rata

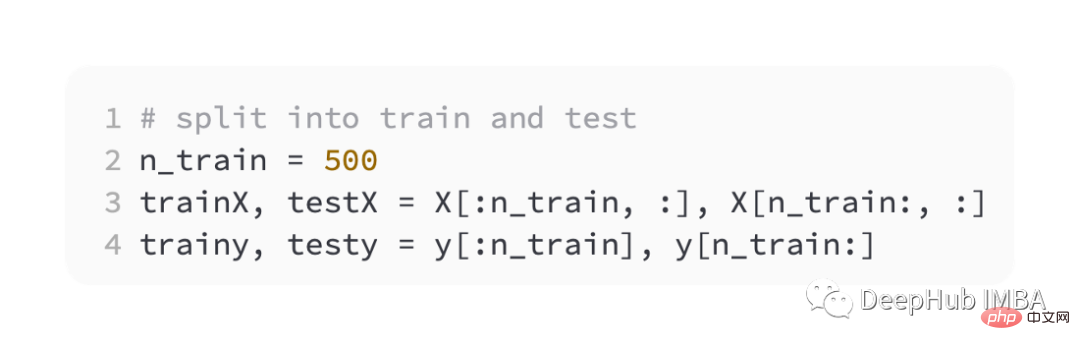
Untuk memperkenalkan fungsi kerugian yang berbeza, kami akan membangunkan berbilang kecil - Model Lapisan Perceptron (MLP).

Mengikut takrifan masalah, terdapat 20 ciri sebagai input, melalui model kami. Nilai sebenar diperlukan untuk meramalkan, jadi lapisan keluaran akan mempunyai nod.

Kami menggunakan SGD untuk pengoptimuman dan mempunyai kadar pembelajaran 0.01 dan momentum 0.9, kedua-duanya adalah nilai lalai yang munasabah. Latihan akan dijalankan selama 100 zaman, set ujian akan dinilai pada akhir setiap peringkat, dan keluk pembelajaran akan diplot.

Selepas model selesai, fungsi kehilangan boleh diperkenalkan:

MSE

Masalah regresi yang paling biasa digunakan ialah min kehilangan ralat kuasa dua (MSE). Ia adalah fungsi kehilangan pilihan di bawah inferens kemungkinan maksimum apabila taburan pembolehubah sasaran ialah Gaussian. Jadi anda hanya perlu menukar kepada fungsi kerugian lain jika anda mempunyai sebab yang lebih baik.

Jika "mse" atau "mean_squared_error" ditentukan sebagai fungsi kehilangan apabila menyusun model dalam Keras, fungsi kehilangan ralat kuasa dua min digunakan.

Kod di bawah ialah contoh lengkap masalah regresi di atas.

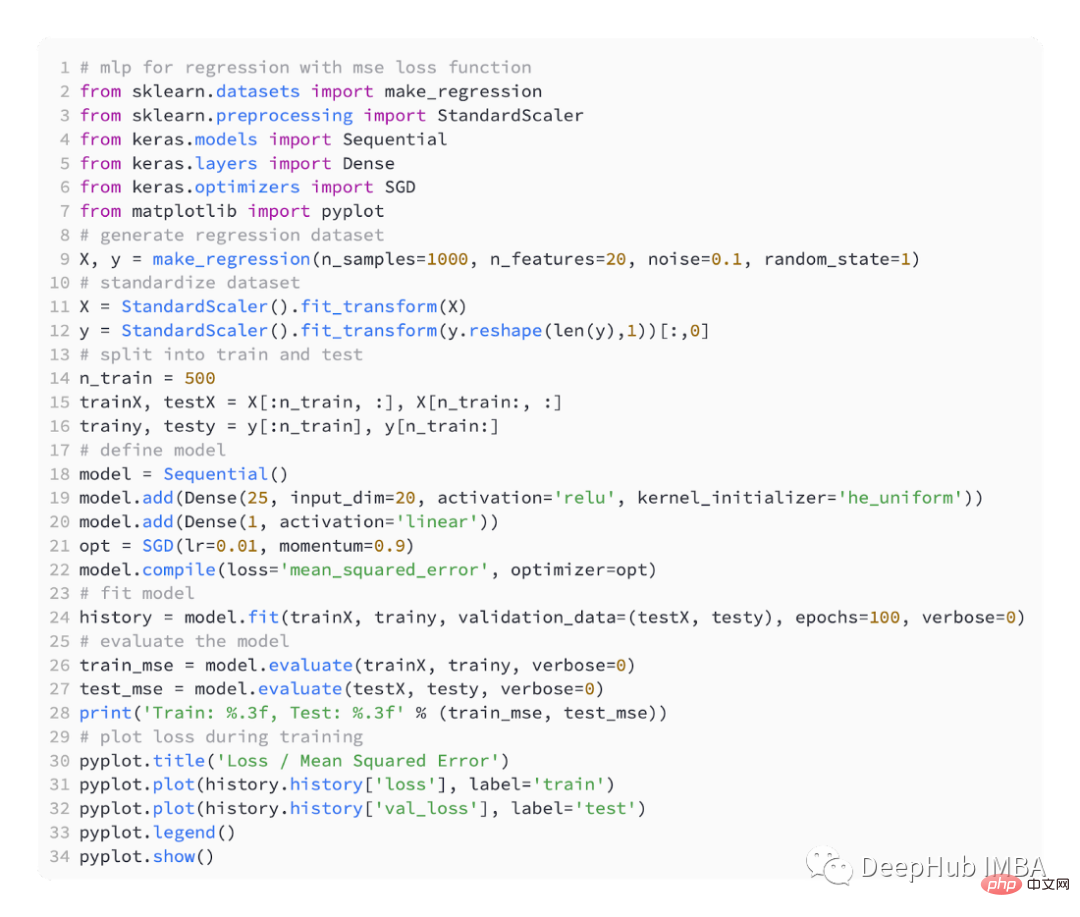
Dalam langkah pertama menjalankan contoh, ralat min kuasa dua bagi set data latihan dan ujian model dicetak Kerana 3 tempat perpuluhan dikekalkan dipaparkan sebagai 0.000

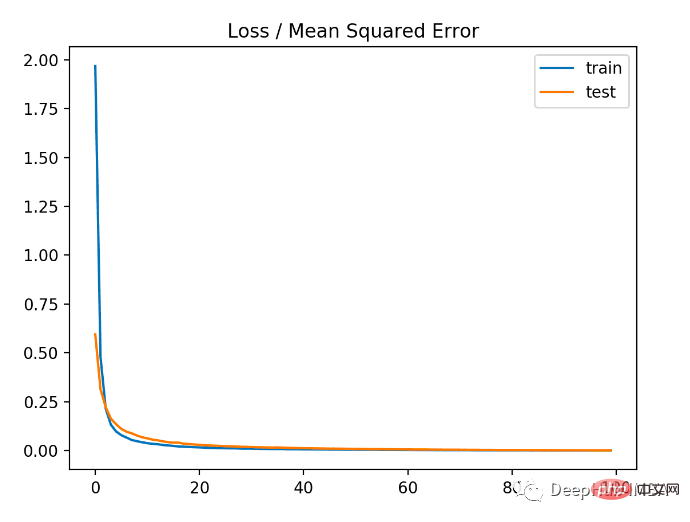
Seperti yang anda boleh lihat daripada rajah di bawah, model menumpu agak cepat dan prestasi latihan dan ujian kekal tidak berubah. Bergantung pada prestasi dan sifat penumpuan model, ralat min kuasa dua ialah pilihan yang baik untuk masalah regresi.

MSLE

Dalam masalah regresi dengan julat nilai yang luas, mungkin tidak diingini untuk menghukum model sebanyak ralat kuasa dua min apabila meramalkan besar nilai. Jadi min ralat kuasa dua boleh dikira dengan terlebih dahulu mengira logaritma asli setiap nilai yang diramalkan. Kehilangan ini dipanggil MSLE, atau min ralat log segi empat sama.

Ia mempunyai kesan melonggarkan kesan penalti apabila terdapat perbezaan besar dalam nilai yang diramalkan. Ia mungkin merupakan ukuran kerugian yang lebih sesuai apabila model secara langsung meramalkan kuantiti tidak berskala.

Menggunakan "mean_squared_logarithmic_error" sebagai fungsi kehilangan dalam keras

Contoh di bawah ialah kod lengkap menggunakan fungsi kehilangan MSLE.

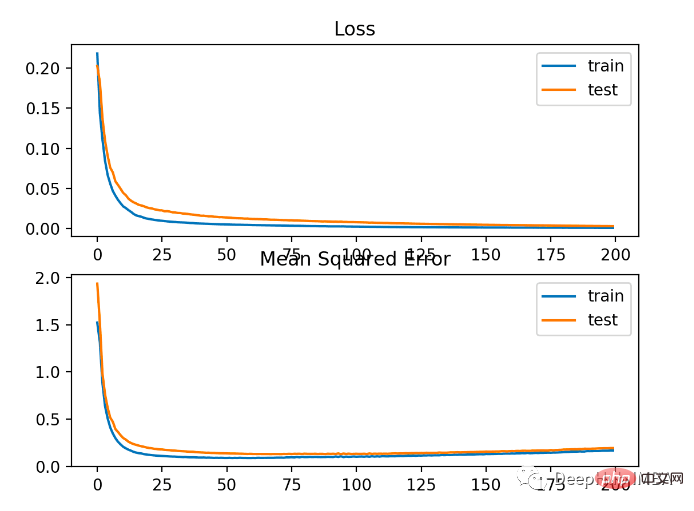
Model mempunyai MSE yang lebih teruk pada set data latihan dan ujian. Ini kerana taburan pembolehubah sasaran adalah taburan Gaussian standard, yang bermaksud bahawa fungsi kehilangan kami mungkin tidak begitu sesuai untuk masalah ini.

Rajah di bawah menunjukkan perbandingan setiap zaman latihan MSE menumpu dengan baik, tetapi MSE mungkin terlalu sesuai kerana ia berkurangan dari zaman 20 kepada berubah dan mula meningkat.

MAE

Bergantung kepada masalah regresi, taburan pembolehubah sasaran mungkin terutamanya Gaussian tetapi mungkin mengandungi outlier seperti nilai besar jauh daripada nilai min atau Kecil.

Dalam kes ini, min ralat mutlak atau kerugian MAE adalah fungsi kerugian yang sesuai kerana ia lebih teguh kepada outlier. Dikira sebagai purata, dengan mengambil kira perbezaan mutlak antara nilai sebenar dan ramalan.

Menggunakan fungsi kehilangan "min_absolute_error"

Berikut ialah kod lengkap menggunakan MAE

Hasilnya Seperti yang ditunjukkan di bawah

Seperti yang anda lihat dalam rajah di bawah, MAE memang bertumpu tetapi ia mempunyai proses yang bergelombang. MAE juga tidak begitu sesuai dalam kes ini kerana pembolehubah sasaran adalah fungsi Gaussian tanpa outlier besar.

Fungsi kehilangan untuk klasifikasi binari

Masalah klasifikasi binari ialah salah satu daripada dua label dalam masalah pemodelan ramalan. Masalah ini ditakrifkan sebagai meramalkan nilai kelas pertama atau kedua sebagai 0 atau 1, dan secara amnya dilaksanakan sebagai meramalkan kebarangkalian tergolong dalam nilai kelas 1.

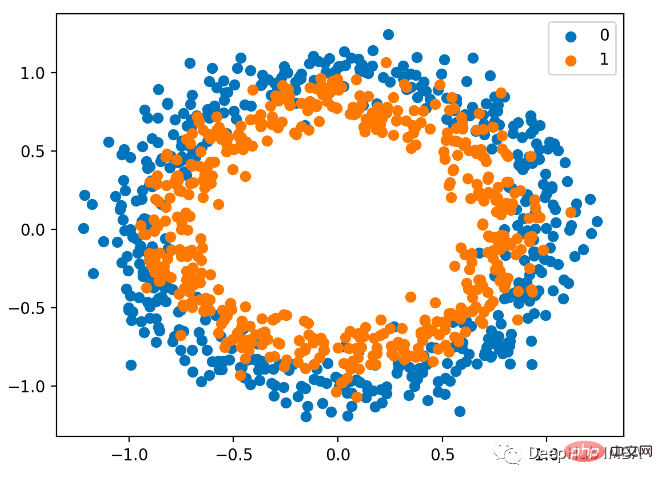
Kami juga menggunakan sklearn untuk menjana data Di sini kami menggunakan masalah bulatan Ia mempunyai satah dua dimensi dengan dua bulatan sepusat tergolong dalam kelas 1. Untuk menjadikan pembelajaran lebih mencabar, kami juga menambahkan bunyi statistik pada sampel. Saiz sampel ialah 1000, dan 10% bunyi statistik ditambah.

Petak sebaran set data boleh membantu kami memahami masalah yang kami modelkan. Disenaraikan di bawah adalah contoh lengkap.

Plot serakan adalah seperti berikut, di mana pembolehubah input menentukan lokasi titik dan warna ialah nilai kelas. 0 ialah biru dan 1 ialah oren.

Ini masih separuh untuk latihan dan separuh lagi untuk ujian

Kami masih mentakrifkan model MLP yang mudah, <.>

dioptimumkan menggunakan SGD, dengan kadar pembelajaran 0.01 dan momentum 0.99.

Model dilatih untuk 200 pusingan pemasangan, dan prestasi model dinilai berdasarkan kehilangan dan ketepatan.

BCE

BCE ialah fungsi kehilangan lalai yang digunakan untuk menyelesaikan masalah klasifikasi binari. Di bawah rangka kerja inferens kemungkinan maksimum, ia adalah fungsi kehilangan pilihan. Untuk ramalan jenis 1, entropi silang mengira skor yang meringkaskan perbezaan purata antara taburan kebarangkalian sebenar dan ramalan.

Apabila menyusun model Keras, binary_crossentropy boleh ditentukan sebagai fungsi kehilangan.

Untuk meramalkan kebarangkalian kelas 1, lapisan keluaran mesti mengandungi nod dan pengaktifan 'sigmoid'.

Berikut ialah kod lengkap:

Model mempelajari masalah dengan agak baik, dalam set data ujian Kadar ketepatan ialah 83% dan kadar ketepatan ialah 85%. Terdapat beberapa tahap pertindihan antara markah, menunjukkan bahawa model tidak terlalu muat atau kurang muat.

Seperti yang ditunjukkan dalam gambar di bawah, kesan latihan adalah sangat baik. Oleh kerana ralat antara taburan kebarangkalian adalah berterusan, plot kehilangan adalah lancar, manakala plot garis ketepatan menunjukkan bonjolan kerana contoh dalam set latihan dan ujian hanya boleh diramalkan sebagai betul atau salah, memberikan maklumat yang kurang berbutir.

Engsel

Model Mesin Vektor Sokongan (SVM) menggunakan fungsi Hinge loss sebagai alternatif kepada cross-entropy untuk menyelesaikan masalah klasifikasi binari.

Nilai sasaran adalah dalam set [-1, 1] , bertujuan untuk digunakan dengan pengelasan binari. Engsel akan mendapat ralat yang lebih besar jika nilai kelas sebenar dan ramalan mempunyai tanda yang berbeza. Ia kadangkala lebih baik daripada entropi silang pada masalah klasifikasi binari.

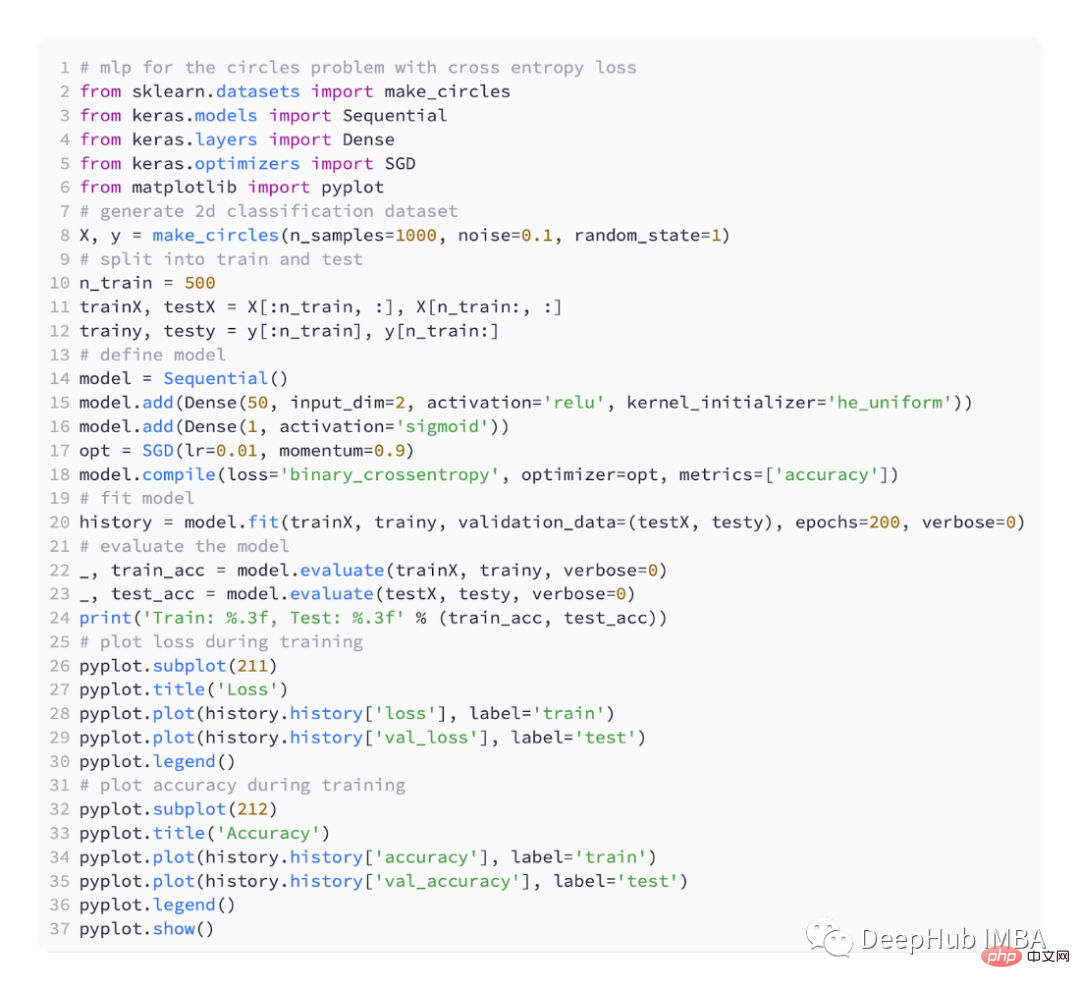
Sebagai langkah pertama, kita perlu mengubah suai nilai pembolehubah sasaran kepada set {-1, 1}.

Ia dipanggil ' engsel ' dalam keras.

Dalam lapisan keluaran rangkaian, satu nod fungsi pengaktifan tanh mesti digunakan untuk mengeluarkan satu nilai antara -1 dan 1.

Berikut ialah kod lengkap:

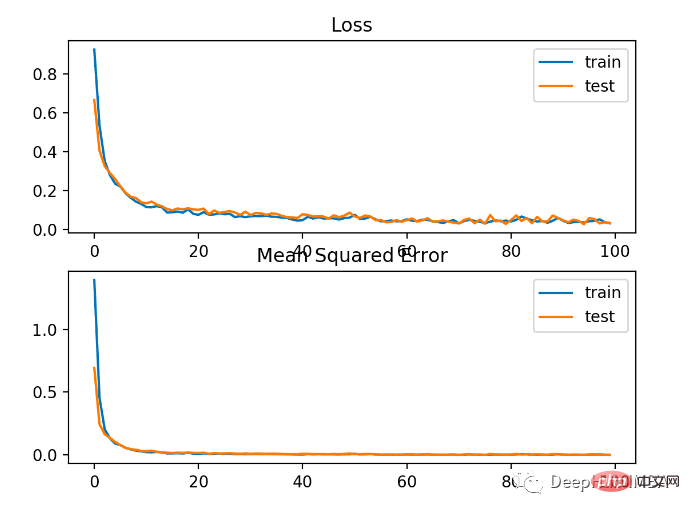
Prestasi yang lebih teruk daripada cross entropy, pada set latihan dan ujian. ketepatan kurang daripada 80%.

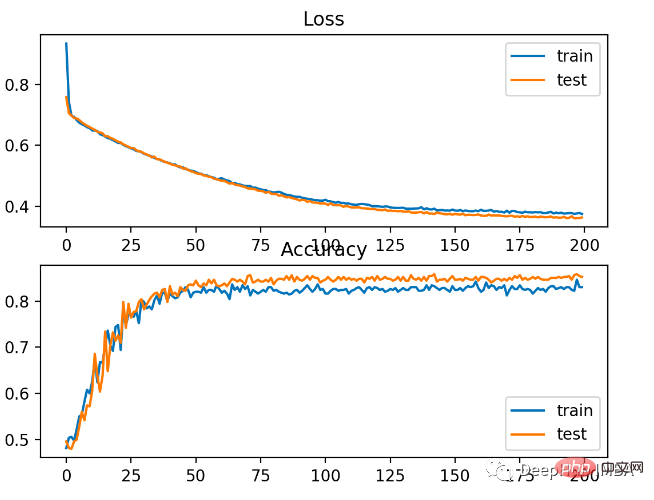
Seperti yang dapat dilihat daripada rajah di bawah, model telah menumpu, dan graf ketepatan pengelasan menunjukkan bahawa ia juga telah menumpu.

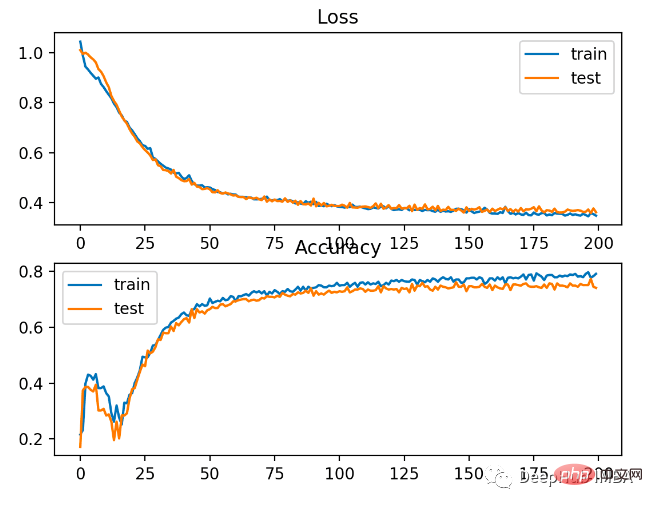
Anda dapat melihat bahawa BCE adalah lebih baik untuk masalah ini. Sebab yang mungkin di sini ialah kami mempunyai beberapa titik bunyi

Atas ialah kandungan terperinci Lima fungsi kehilangan yang biasa digunakan untuk melatih rangkaian saraf pembelajaran mendalam. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!