Bilangan kertas telah meningkat secara mendadak dalam tempoh sepuluh tahun yang lalu. Bagaimanakah pembelajaran mendalam perlahan-lahan membuka pintu kepada penaakulan matematik?

Penaakulan matematik ialah manifestasi utama kecerdasan manusia, membolehkan kita memahami dan membuat keputusan berdasarkan data berangka dan bahasa. Penaakulan matematik digunakan untuk pelbagai bidang, termasuk sains, kejuruteraan, kewangan dan kehidupan seharian, dan merangkumi pelbagai kebolehan daripada kemahiran asas seperti pengecaman corak dan pecah nombor kepada kemahiran lanjutan seperti penyelesaian masalah, penaakulan logik dan pemikiran abstrak.

Membangunkan sistem AI yang boleh menyelesaikan masalah matematik dan membuktikan teorem matematik telah lama menjadi tumpuan penyelidikan dalam bidang pembelajaran mesin dan pemprosesan bahasa semula jadi. Ini juga bermula pada tahun 1960-an.

Dalam sepuluh tahun yang lalu sejak kebangkitan pembelajaran mendalam, minat orang ramai dalam bidang ini telah berkembang dengan ketara:

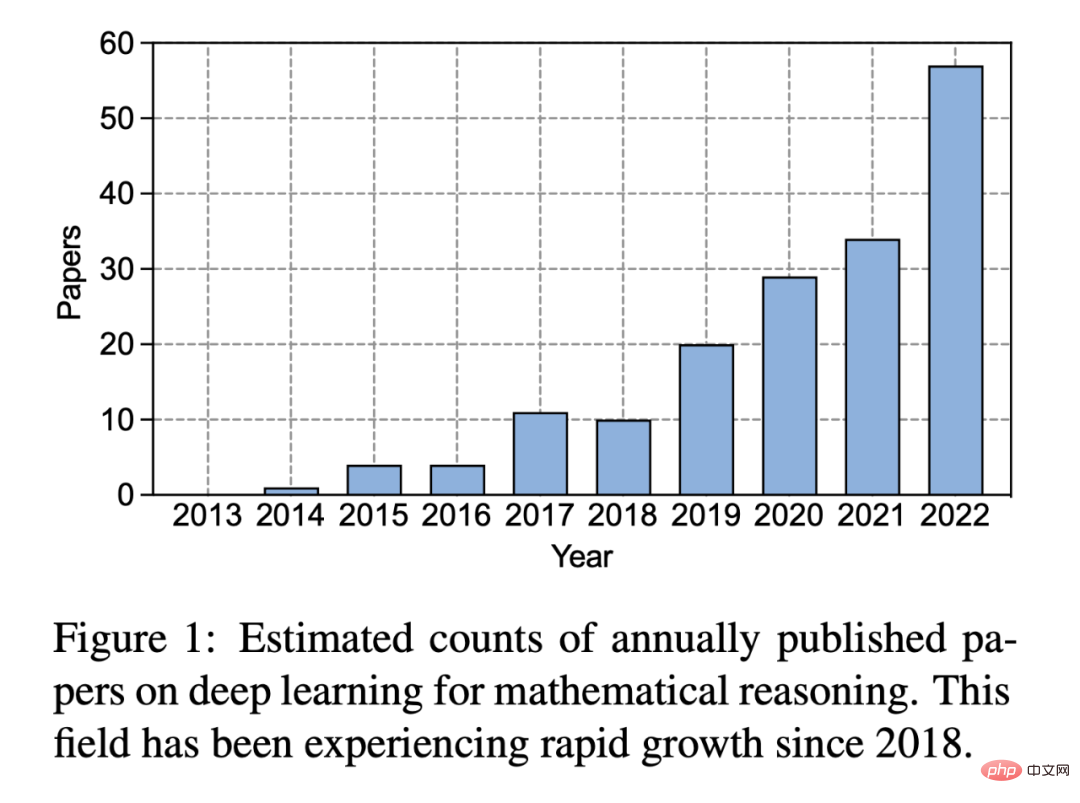
Rajah 1: Anggaran bilangan kertas pembelajaran mendalam diterbitkan setiap tahun mengenai penaakulan matematik. Sejak 2018, kawasan ini telah mengalami pertumbuhan pesat.

Pembelajaran mendalam telah menunjukkan kejayaan besar dalam pelbagai tugas pemprosesan bahasa semula jadi, seperti menjawab soalan dan terjemahan mesin. Begitu juga, penyelidik telah membangunkan pelbagai kaedah rangkaian saraf untuk penaakulan matematik, yang telah terbukti berkesan dalam mengendalikan tugas yang kompleks seperti masalah perkataan, pembuktian teorem, dan penyelesaian masalah geometri. Sebagai contoh, penyelesai masalah aplikasi berasaskan pembelajaran mendalam mengguna pakai rangka kerja urutan ke turutan dan menggunakan mekanisme perhatian sebagai langkah perantaraan untuk menjana ungkapan matematik. Tambahan pula, dengan model korpora dan Transformer berskala besar, model bahasa pra-latihan telah mencapai keputusan yang menjanjikan dalam pelbagai tugasan matematik. Baru-baru ini, model bahasa besar seperti GPT-3 telah memajukan lagi bidang penaakulan matematik dengan menunjukkan keupayaan yang mengagumkan dalam penaakulan yang kompleks dan pembelajaran kontekstual.

Dalam laporan yang dikeluarkan baru-baru ini, penyelidik dari UCLA dan institusi lain secara sistematik menyemak kemajuan pembelajaran mendalam dalam penaakulan matematik.

Pautan kertas: https://arxiv.org/pdf/2212.10535.pdf

Alamat projek: https://github.com/lupantech/dl4math

Secara khusus, artikel ini membincangkan pelbagai tugasan dan set data (Bahagian 2) , dan mengkaji kemajuan dalam rangkaian saraf (Bahagian 3) dan model bahasa pralatihan (Bahagian 4) dalam matematik. Perkembangan pesat pembelajaran kontekstual model bahasa besar dalam penaakulan matematik juga diterokai (Bahagian 5). Artikel tersebut menganalisis lebih lanjut penanda aras sedia ada dan mendapati bahawa kurang perhatian diberikan kepada persekitaran multimodal dan sumber rendah (Bahagian 6.1). Penyelidikan berasaskan bukti menunjukkan bahawa perwakilan semasa keupayaan pengkomputeran adalah tidak mencukupi dan kaedah pembelajaran mendalam adalah tidak konsisten berkenaan dengan penaakulan matematik (Bahagian 6.2). Selepas itu, penulis mencadangkan penambahbaikan kepada kerja semasa dari segi generalisasi dan keteguhan, penaakulan yang boleh dipercayai, pembelajaran daripada maklum balas, dan penaakulan matematik multimodal (Bahagian 7).

Tugasan dan Set Data

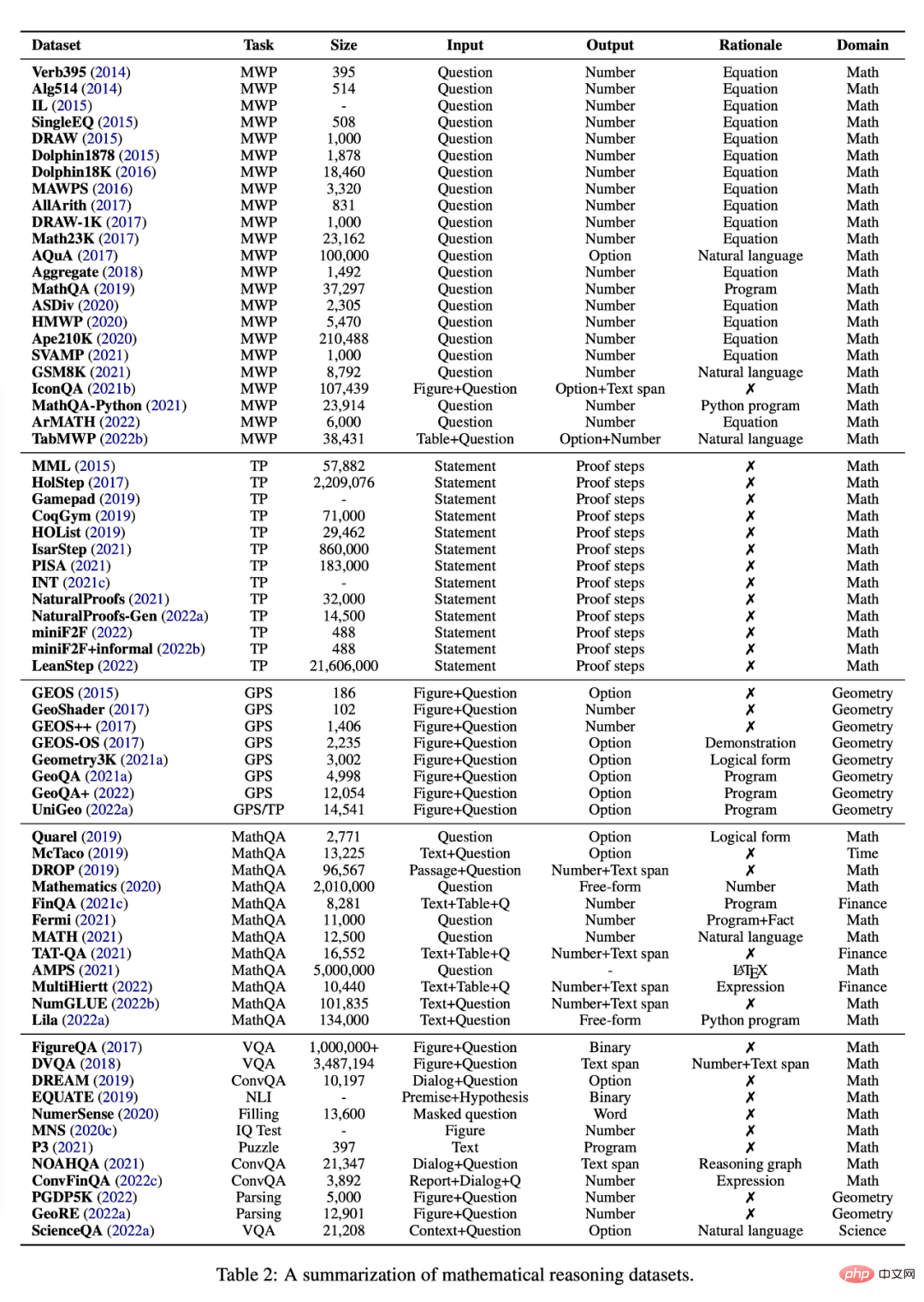
Bahagian ini mengkaji pelbagai tugasan dan set data yang tersedia pada masa ini untuk mengkaji penaakulan matematik menggunakan kaedah pembelajaran mendalam, lihat Jadual 2.

Masalah Perkataan Matematik (Masalah Perkataan Matematik)

Masalah perkataan mengandungi naratif pendek yang melibatkan orang, entiti, dan kuantiti yang hubungan matematiknya boleh dimodelkan oleh satu set persamaan yang penyelesaiannya mendedahkan jawapan akhir kepada masalah tersebut. Jadual 1 adalah contoh biasa. Soalan melibatkan empat operasi asas matematik iaitu tambah, tolak, darab dan bahagi, dengan langkah tunggal atau berbilang. Cabaran masalah aplikasi kepada sistem NLP terletak pada permintaan untuk pemahaman bahasa, analisis semantik dan pelbagai keupayaan penaakulan matematik.

Data data masalah perkataan sedia ada merangkumi soalan peringkat sekolah rendah yang dikikis daripada tapak web pembelajaran dalam talian, dikumpulkan daripada buku teks atau dianotasi secara manual oleh manusia. Set data masalah perkataan awal agak kecil atau terhad kepada sebilangan kecil langkah. Beberapa set data terkini bertujuan untuk meningkatkan kepelbagaian dan kesukaran masalah. Sebagai contoh, Ape210K, set masalah awam terbesar semasa, terdiri daripada 210k masalah perkataan sekolah rendah manakala masalah dalam GSM8K boleh melibatkan sehingga 8 langkah penyelesaian. SVAMP ialah penanda aras yang menguji keteguhan model pembelajaran mendalam kepada masalah perkataan dengan variasi mudah. Beberapa set data yang ditubuhkan baru-baru ini juga melibatkan modaliti selain daripada teks. Sebagai contoh, IconQA menyediakan gambar rajah abstrak sebagai latar belakang visual, manakala TabMWP menyediakan latar belakang jadual untuk setiap soalan.

Kebanyakan set data masalah perkataan memberikan justifikasi untuk persamaan beranotasi sebagai penyelesaian (lihat Jadual 1). Untuk meningkatkan prestasi dan kebolehtafsiran penyelesai yang dipelajari, MathQA dianotasi dengan prosedur pengiraan yang tepat, dan MathQA-Python menyediakan prosedur Python yang konkrit. Set data lain menjelaskan soalan dengan penyelesaian bahasa semula jadi berbilang langkah yang dianggap lebih sesuai untuk bacaan manusia. Lila menganotasi banyak set data masalah perkataan yang dinyatakan sebelum ini menggunakan prinsip pengaturcaraan Python.

Pembuktian Teori

Mengautomasikan pembuktian teorem ialah cabaran jangka panjang dalam bidang AI. Masalah biasanya melibatkan pembuktian kebenaran teorem matematik melalui satu siri hujah logik. Pembuktian teorem melibatkan pelbagai kemahiran, seperti memilih strategi pelbagai langkah yang cekap, menggunakan pengetahuan latar belakang, dan melaksanakan operasi simbolik seperti aritmetik atau terbitan.

Baru-baru ini, terdapat minat yang semakin meningkat dalam menggunakan model bahasa untuk pembuktian teorem dalam pembukti teorem interaktif formal (ITP). Teorem dinyatakan dalam bahasa pengaturcaraan ITP dan kemudian dipermudahkan dengan menjana "langkah bukti" sehingga ia dikurangkan kepada fakta yang diketahui. Hasilnya ialah urutan langkah yang membentuk bukti yang disahkan.

Pembuktian teorem tidak formal mencadangkan satu lagi medium pembuktian teorem, iaitu menggunakan campuran bahasa semula jadi dan tatatanda matematik "standard" (seperti LATEX) untuk menulis pernyataan dan bukti dan disemak untuk kebenaran oleh manusia.

Bidang penyelidikan yang baru muncul bertujuan untuk menggabungkan unsur pembuktian teorem tidak formal dan formal. Sebagai contoh, Wu et al. (2022b) meneroka menterjemah kenyataan tidak formal kepada kenyataan formal, manakala Jiang et al (2022b) mengeluarkan versi baharu penanda aras miniF2F yang menambah kenyataan dan bukti tidak formal, yang dipanggil miniF2F+informal. Jiang et al. (2022b) meneroka menukar bukti tidak formal yang disediakan (atau dijana) kepada bukti formal.

Masalah Geometri

Penyelesaian Automatik Masalah Geometri (GPS) juga merupakan kecerdasan buatan yang telah lama wujud dalam matematik menaakul misi penyelidikan dan telah menarik perhatian meluas dalam beberapa tahun kebelakangan ini. Tidak seperti masalah perkataan, masalah geometri terdiri daripada huraian teks bahasa semula jadi dan angka geometri. Seperti yang ditunjukkan dalam Rajah 2, input multimodal menerangkan entiti, sifat dan hubungan unsur geometri, manakala matlamatnya adalah untuk mencari penyelesaian berangka kepada pembolehubah yang tidak diketahui. GPS adalah tugas yang mencabar untuk kaedah pembelajaran mendalam kerana kemahiran kompleks yang diperlukan. Ia melibatkan keupayaan untuk menghuraikan maklumat multimodal, melibatkan diri dalam abstraksi simbolik, menggunakan pengetahuan teorem, dan terlibat dalam penaakulan kuantitatif.

Set data awal telah mempromosikan penyelidikan dalam bidang ini, namun set data ini agak kecil atau tidak tersedia secara umum, yang mengehadkan pembangunan kaedah pembelajaran mendalam. Untuk menangani had ini, Lu et al mencipta dataset Geometry3K, yang terdiri daripada 3002 soalan geometri aneka pilihan yang dianotasi dalam bentuk logik bersatu untuk input multimodal. Baru-baru ini, set data berskala lebih besar seperti GeoQA, GeoQA+ dan UniGeo telah diperkenalkan dan diberi anotasi dengan program yang boleh dipelajari dan dilaksanakan oleh penyelesai saraf untuk mendapatkan jawapan akhir.

Soal Jawab Matematik

Penyelidikan terkini menunjukkan bahawa sistem penaakulan matematik SOTA mungkin "rapuh" dalam penaakulan, iaitu model bergantung pada isyarat palsu daripada set data tertentu dan pengiraan plug-and-play untuk mencapai prestasi "memuaskan". Bagi menyelesaikan masalah ini, penanda aras baru telah dicadangkan dari pelbagai aspek. Set data Matematik (Saxton et al., 2020) merangkumi pelbagai jenis masalah matematik, merangkumi aritmetik, algebra, kebarangkalian dan kalkulus. Set data ini boleh mengukur keupayaan generalisasi algebra model. Begitu juga, MATH (Hendrycks et al., 2021) terdiri daripada matematik persaingan yang mencabar untuk mengukur keupayaan penyelesaian masalah model dalam situasi yang kompleks.

Sesetengah kerja untuk menambah latar belakang jadual pada input soalan. Contohnya, FinQA, TAT-QA dan MultiHiertt mengumpul soalan yang memerlukan pemahaman jadual dan penaakulan berangka untuk dijawab. Sesetengah kajian telah mencadangkan penanda aras bersatu untuk penaakulan berangka berskala besar. NumGLUE (Mishra et al., 2022b) ialah penanda aras pelbagai tugas yang bertujuan untuk menilai prestasi model pada lapan tugasan yang berbeza. Mishra et al. 2022a meneruskan hala tuju ini dengan mencadangkan Lila, yang terdiri daripada 23 tugasan penaakulan berangka yang merangkumi pelbagai topik matematik, kerumitan bahasa, format soalan dan keperluan pengetahuan latar belakang.

AI juga telah membuat pencapaian dalam jenis masalah kuantitatif yang lain. Nombor, carta dan lukisan, sebagai contoh, adalah media penting untuk menyampaikan sejumlah besar maklumat secara ringkas. FigureQA, DVQA, MNS, PGDP5K dan GeoRE semuanya diperkenalkan untuk mengkaji keupayaan model untuk menaakul tentang hubungan kuantitatif antara entiti berasaskan graf. NumerSense menyiasat sama ada dan sejauh mana model bahasa pra-latihan sedia ada dapat merasakan pengetahuan akal sehat berangka. EQUATE memformalkan pelbagai aspek penaakulan kuantitatif dalam rangka kerja penaakulan bahasa semula jadi. Penaakulan kuantitatif juga kerap muncul dalam bidang tertentu seperti kewangan, sains dan pengaturcaraan. Sebagai contoh, ConvFinQA melakukan penaakulan berangka pada laporan kewangan dalam bentuk soalan dan jawapan perbualan ScienceQA melibatkan penaakulan berangka dalam bidang saintifik dan P3 menyiasat keupayaan penaakulan fungsi model pembelajaran mendalam untuk mencari input yang sah untuk program yang diberikan; betul.

Rangkaian Neural untuk Penaakulan Matematik

Pengarang artikel ini juga merumuskan beberapa rangkaian saraf biasa yang digunakan untuk penaakulan matematik.

Rangkaian Seq2Seq

Rangkaian neural Seq2Seq telah berjaya digunakan pada tugasan penaakulan matematik, seperti masalah aplikasi dan teorem bukti, soalan geometri dan jawapan soalan matematik. Model Seq2Seq menggunakan seni bina penyahkod pengekod yang biasanya memformalkan penaakulan matematik sebagai tugas penjanaan jujukan. Idea asas kaedah ini adalah untuk memetakan urutan input (seperti masalah matematik) kepada urutan output (seperti persamaan, program, dan bukti). Pengekod dan penyahkod biasa termasuk rangkaian memori jangka pendek (LSTM) dan unit berulang berpagar (GRU). Kerja yang meluas telah menunjukkan bahawa model Seq2Seq mempunyai kelebihan prestasi berbanding kaedah pembelajaran statistik sebelumnya, termasuk varian dua arah BiLSTM dan BiGRU. DNS ialah kerja pertama menggunakan model Seq2Seq untuk menukar ayat daripada masalah perkataan kepada persamaan matematik.

Rangkaian berasaskan graf

Pendekatan Seq2Seq mempunyai kelebihan menjana ungkapan matematik dan tidak bergantung pada tangan- ciri yang dibuat. Ungkapan matematik boleh diubah menjadi struktur berasaskan pokok, seperti pokok sintaks abstrak (AST) dan struktur berasaskan graf, yang menerangkan maklumat berstruktur dalam ungkapan tersebut. Walau bagaimanapun, maklumat penting ini tidak dimodelkan secara eksplisit oleh pendekatan Seq2Seq. Untuk menyelesaikan masalah ini, penyelidik membangunkan rangkaian neural berasaskan graf untuk memodelkan struktur secara eksplisit dalam ekspresi.

Model Jujukan-ke-pokok (Seq2Tree) memodelkan struktur pokok secara eksplisit apabila mengekod jujukan output. Sebagai contoh, Liu et al mereka bentuk model Seq2Tree untuk menggunakan maklumat persamaan AST dengan lebih baik. Sebaliknya, Seq2DAG menggunakan rangka kerja graf jujukan (Seq2Graph) apabila menjana persamaan kerana penyahkod graf dapat mengekstrak hubungan kompleks antara berbilang pembolehubah. Maklumat berasaskan graf juga boleh dibenamkan apabila mengekod urutan matematik input. Sebagai contoh, ASTactic menggunakan TreeLSTM pada AST untuk mewakili matlamat input dan premis pembuktian teorem.

Rangkaian berasaskan perhatian​

Mekanisme perhatian telah berjaya digunakan pada pemprosesan bahasa semula jadi dan masalah penglihatan komputer, dengan mengambil kira input vektor tersembunyi semasa proses penyahkodan. Penyelidik telah meneroka peranannya dalam tugasan penaakulan matematik kerana ia boleh digunakan untuk mengenal pasti hubungan yang paling penting antara konsep matematik. Sebagai contoh, MATH-EN ialah penyelesai masalah perkataan yang mendapat manfaat daripada maklumat pergantungan jarak jauh yang dipelajari melalui perhatian kendiri. Kaedah berasaskan perhatian juga telah digunakan untuk tugasan penaakulan matematik yang lain, seperti masalah geometri dan pembuktian teorem. Untuk mengekstrak perwakilan yang lebih baik, pelbagai mekanisme perhatian telah dikaji, seperti Kumpulan-ATT, yang menggunakan perhatian berbilang kepala yang berbeza untuk mengekstrak pelbagai jenis ciri MWP, dan perhatian graf, yang digunakan untuk mengekstrak maklumat sedar pengetahuan.

Rangkaian Neural Lain

Kaedah pembelajaran mendalam untuk tugasan penaakulan matematik juga boleh menggunakan rangkaian saraf lain, seperti sebagai rangkaian Neural convolutions dan rangkaian multimodal. Sesetengah karya menggunakan seni bina rangkaian saraf konvolusi untuk mengekod teks input, memberikan model keupayaan untuk menangkap hubungan jangka panjang antara simbol dalam input. Sebagai contoh, Irving et al mencadangkan aplikasi pertama rangkaian saraf dalam dalam pembuktian teorem, yang bergantung pada rangkaian konvolusi untuk pemilihan premis dalam teori besar.

Tugas penaakulan matematik berbilang mod, seperti penyelesaian masalah geometri dan penaakulan matematik berasaskan graf, diformalkan sebagai soalan menjawab soalan visual (VQA). Dalam domain ini, input visual dikodkan menggunakan ResNet atau Faster-RCNN, manakala perwakilan teks diperoleh melalui GRU atau LTSM. Selepas itu, perwakilan bersama dipelajari menggunakan model gabungan pelbagai mod seperti BAN, FiLM, dan DAFA.

Struktur rangkaian saraf dalam yang lain juga boleh digunakan untuk penaakulan matematik. Zhang et al mengeksploitasi kejayaan rangkaian saraf graf (GNN) dalam penaakulan spatial dan menggunakannya untuk masalah geometri. WaveNet digunakan untuk pembuktian teorem kerana keupayaannya untuk menyelesaikan data siri masa membujur. Tambahan pula, Transformer didapati mengatasi GRU dalam menghasilkan persamaan matematik dalam DDT. Dan, MathDQN ialah kerja pertama meneroka pembelajaran pengukuhan untuk menyelesaikan masalah perkataan matematik, terutamanya memanfaatkan keupayaan cariannya yang berkuasa.

Model bahasa pra-latihan untuk penaakulan matematik

Model bahasa pra-latihan telah menunjukkan peningkatan prestasi yang ketara pada pelbagai tugas NLP, juga digunakan pada isu berkaitan matematik , kerja terdahulu telah menunjukkan bahawa model bahasa yang telah dilatih berprestasi baik dalam menyelesaikan masalah perkataan, membantu dengan pembuktian teorem dan tugasan matematik yang lain. Walau bagaimanapun, menggunakannya untuk penaakulan matematik memberikan beberapa cabaran.

Pertama sekali, model bahasa pra-latihan tidak dilatih secara khusus pada data matematik. Ini mungkin menyebabkan penguasaan mereka yang lebih rendah dalam tugasan berkaitan matematik berbanding tugasan bahasa semula jadi. Terdapat juga kurang data matematik atau saintifik yang tersedia untuk pra-latihan berskala besar berbanding dengan data teks.

Kedua, saiz model pra-latihan terus berkembang, menjadikannya mahal untuk melatih keseluruhan model dari awal untuk tugas hiliran tertentu.

Selain itu, tugasan hiliran mungkin mengendalikan format atau modaliti input yang berbeza, seperti jadual atau carta berstruktur. Untuk menangani cabaran ini, penyelidik mesti memperhalusi model pralatihan atau menyesuaikan seni bina saraf pada tugas hiliran.

Akhir sekali, walaupun model bahasa pra-latihan boleh mengekod sejumlah besar maklumat bahasa, daripada matlamat pemodelan bahasa sahaja, model mungkin sukar untuk mempelajari perwakilan berangka atau tinggi. -kemahiran menaakul peringkat. Dengan pemikiran ini, penyelidikan baru-baru ini telah menyiasat penyerapan kemahiran berkaitan matematik dalam kursus yang bermula dengan asas.

Pembelajaran matematik penyeliaan kendiri

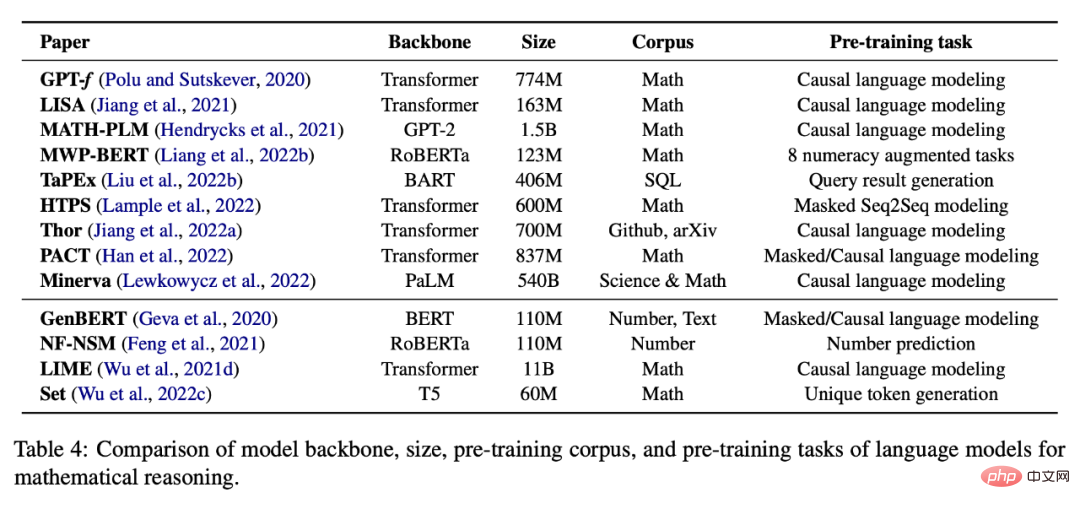
Jadual 4 di bawah menyediakan tugasan penyeliaan kendiri terlatih untuk matematik penaakulan Senarai model bahasa.

Penalaan halus matematik khusus tugasan

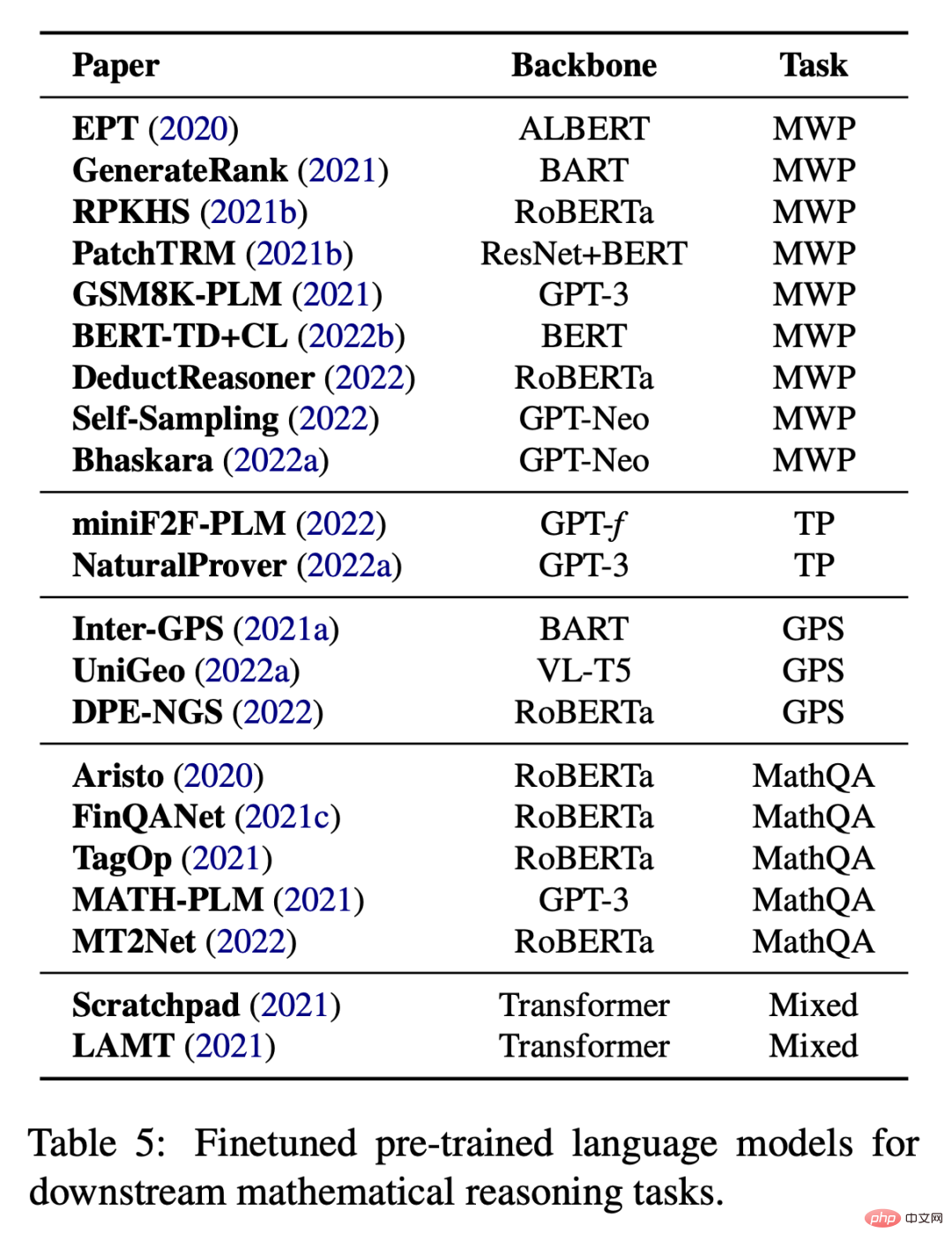
Apabila tiada data yang mencukupi untuk Penalaan halus khusus tugas juga merupakan amalan biasa apabila melatih model besar dari awal. Seperti yang ditunjukkan dalam Jadual 5, kerja sedia ada cuba untuk memperhalusi model bahasa pra-latihan pada pelbagai tugas hiliran.

Selain memperhalusi parameter model, banyak karya juga menggunakan model bahasa pra-latihan sebagai pengekod dan menggabungkannya dengan modul lain untuk menyelesaikan tugas hiliran Contohnya, IconQA mencadangkan untuk menggunakan ResNet dan BERT untuk pengecaman graf dan pengecaman graf masing-masing.

Pembelajaran konteks dalam penaakulan matematik

Sampel konteks biasanya mengandungi pasangan input-output dan beberapa perkataan gesaan, sebagai contoh, sila pilih nombor terbesar daripada senarai .

Input: [2, 4, 1, 5, 8]

Output: 8.

Pembelajaran beberapa pukulan memberikan berbilang sampel, dan kemudian model meramalkan output pada sampel input terakhir. Walau bagaimanapun, dorongan beberapa pukulan standard ini, yang menyediakan model bahasa besar dengan sampel kontekstual pasangan input-output sebelum sampel masa ujian, belum terbukti mencukupi untuk mencapai prestasi yang baik pada tugas yang mencabar seperti penaakulan matematik.

Gesaan rantaian pemikiran (CoT) menggunakan penjelasan bahasa semula jadi perantaraan sebagai gesaan, membenarkan model bahasa besar menjana rantaian penaakulan dahulu dan kemudian meramalkan jawapan kepada input soalan. Sebagai contoh, gesaan CoT untuk menyelesaikan masalah perkataan boleh menjadi "Mari kita fikir langkah demi langkah!" akan menjadikan model bahasa besar sebagai penaakulan sifar. Selain daripada ini, kerja terbaharu telah menumpukan pada cara memperbaik penaakulan rantaian pemikiran dalam penetapan inferens pukulan sifar. Jenis kerja ini terbahagi kepada dua bahagian: (i) memilih sampel kontekstual yang lebih baik dan (ii) mencipta rantaian inferens yang lebih baik.

Pemilihan sampel konteks

Kerja rantaian pemikiran awal ialah memilih sampel konteks secara rawak atau heuristik. Penyelidikan terkini telah menunjukkan bahawa jenis pembelajaran beberapa pukulan ini boleh menjadi sangat tidak stabil di bawah pilihan contoh kontekstual yang berbeza. Oleh itu, sampel penaakulan kontekstual yang boleh membuat gesaan yang paling cekap masih menjadi isu yang tidak diketahui dalam kalangan akademik. Untuk menangani had ini, beberapa karya terbaru telah mengkaji pelbagai kaedah untuk mengoptimumkan proses pemilihan sampel konteks. Sebagai contoh, Rubin et al (2022) cuba menyelesaikan masalah ini dengan mendapatkan sampel yang serupa secara semantik. Walau bagaimanapun, pendekatan ini tidak berfungsi dengan baik pada masalah penaakulan matematik, dan sukar untuk mengukur persamaan jika maklumat berstruktur (seperti jadual) disertakan. Di samping itu, Fu et al. (2022) mencadangkan gesaan berasaskan kerumitan, memilih sampel dengan rantaian penaakulan yang kompleks (iaitu, rantaian dengan lebih banyak langkah penaakulan) sebagai gesaan. Lu et al (2022b) mencadangkan kaedah untuk memilih sampel kontekstual melalui pembelajaran pengukuhan. Khususnya, ejen belajar untuk mencari sampel kontekstual terbaik daripada kumpulan calon, dengan matlamat untuk memaksimumkan ganjaran yang diramalkan untuk sampel latihan yang diberikan apabila berinteraksi dengan persekitaran GPT-3. Tambahan pula, Zhang et al (2022b) mendapati bahawa kepelbagaian masalah contoh juga boleh meningkatkan prestasi model. Mereka mencadangkan pendekatan dua langkah untuk membina contoh masalah dalam konteks: pertama, bahagikan masalah set data yang diberikan kepada beberapa kumpulan kedua, pilih masalah yang mewakili daripada setiap kumpulan dan gunakan Rantaian pemikiran sifar pukulan heuristik yang mudah menghasilkan rantaian penaakulannya; .

Rantai penaakulan berkualiti tinggi

​

Kerja rantaian pemikiran awal terutamanya bergantung pada rantaian penaakulan beranotasi manusia sebagai segera . Walau bagaimanapun, mencipta rantaian penaakulan secara manual mempunyai dua kelemahan: pertama, apabila tugasan menjadi semakin kompleks, model semasa mungkin tidak mencukupi untuk belajar melaksanakan semua langkah penaakulan yang diperlukan dan tidak boleh digeneralisasikan dengan mudah kepada tugasan yang berbeza, satu proses penyahkodan mudah dipengaruhi oleh langkah penaakulan yang salah, yang membawa kepada ramalan yang salah dalam jawapan akhir. Untuk menangani batasan ini, penyelidikan terkini tertumpu terutamanya pada dua aspek: (i) membuat contoh yang lebih kompleks, dikenali sebagai kaedah berasaskan proses (ii) menggunakan kaedah seperti ensemble, yang dikenali sebagai kaedah berasaskan hasil. Selepas menilai tanda aras dan kaedah sedia ada, penulis turut membincangkan hala tuju penyelidikan masa depan dalam bidang ini. Untuk butiran penyelidikan lanjut, sila rujuk kertas asal.

Atas ialah kandungan terperinci Bilangan kertas telah meningkat secara mendadak dalam tempoh sepuluh tahun yang lalu. Bagaimanakah pembelajaran mendalam perlahan-lahan membuka pintu kepada penaakulan matematik?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!