NP benar-benar retak biri-biri dan kehilangan biri-biri?

Baru-baru ini, Yang Liao Ge Yang telah menjadi popular di Internet Terdapat lebih banyak artikel tentang betapa sukarnya tahap kedua dan cara untuk melepasinya kerumitan pengiraan. Artikel itu mungkin belum wujud, jadi kali ini saya juga akan menulis artikel tentang kerumitan pengiraan untuk dicuba.

Mekanisme permainan agak mudah, terdapat beberapa jenis blok pada peta Pemain boleh memilih blok dan meletakkannya ke dalam slot mereka sendiri (slot mempunyai bahagian atas had. adalah pemalar), jika terdapat tiga blok daripada jenis yang sama dalam slot, mereka akan dihapuskan Matlamat permainan adalah untuk menghapuskan semua blok. Kesukaran permainan ialah blok pada peta disusun Blok yang disusun di bawah tidak boleh dipilih (iaitu, tidak berkunci) selepas blok di atas dimasukkan ke dalam slot Jenisnya tidak diketahui kerana dikaburkan.

Malah, mekanisme Sheep of a Sheep sangat serupa dengan beberapa permainan mini, dan banyak daripada permainan mini ini telah terbukti lengkap dengan NP, jadi kami agak yakin bahawa kami juga boleh membuktikan promosi Mempunyai biri-biri adalah NP-lengkap. Di sini kami memberikan struktur pengurangan yang agak lemah dan mudah untuk menggambarkan bahawa permainan domba-ke-biri yang digalakkan adalah NP-lengkap. Generalisasi yang kita bincangkan di sini bermakna bilangan jenis blok tidak terhad kepada pemalar, jenis blok yang disekat ditentukan dan diketahui, dan bilangan slot ditetapkan pada 3 (kaedah yang serupa boleh digunakan jika bilangan slot adalah pemalar lain, selagi Pada permulaan permainan, pemain terpaksa mengambil jenis blok khas, yang hanya boleh dihapuskan pada akhir permainan Semasa keseluruhan proses, blok ini menduduki slot. yang bersamaan dengan kehilangan slot). Sudah tentu, kami tidak menganggap kesan alat peraga permainan di sini.

Pengurangan dalam artikel ini kebanyakannya diciplak daripada halaman web Computational Complexity of Games and Puzzles yang membuktikan bahawa permainan Mah-Jongg (permainan yang serupa dengan Lianliankan, juga dipanggil Mahjong di beberapa tempat ) ialah NP -penurunan lengkap.

Kami masih menggunakan masalah NP-lengkap klasik 3-SAT sebagai masalah pengurangan. Kami menyediakan 3 cerucuk persegi untuk setiap pembolehubah dalam formula 3-SAT, satu cerucuk persegi digunakan untuk mensimulasikan tugasan pembolehubah (BENAR atau SALAH), satu cerucuk persegi sepadan dengan tugasan FALSE, dan satu cerucuk sepadan dengan penugasan BENAR. Timbunan blok tugasan untuk pembolehubah simulasi mempunyai dua peringkat Tahap pertama mengandungi 4 blok yang sama sepadan dengan pembolehubah Tahap kedua mengandungi satu blok setiap satu dengan pembolehubah ditetapkan kepada BENAR dan SALAH dan blok pengisian. Timbunan blok yang sepadan dengan nilai yang diberikan kepada FALSE biasanya berbilang lapisan (juga boleh dikurangkan kepada satu lapisan Lapisan atas mengandungi dua blok yang sepadan dengan pembolehubah yang diberikan kepada FALSE (untuk digunakan dengan timbunan blok yang telah ditetapkan sebelumnya). dan lapisan bawah mengandungi blok yang sepadan dengan pembolehubah yang diberikan kepada petak Klausa (bersamaan dengan klausa di mana pembolehubah muncul sebagai tidak) dan petak pengisi. Struktur yang sepadan dengan timbunan blok yang diberikan TRUE adalah serupa. Akhir sekali, terdapat longgokan petak yang digunakan untuk mengesahkan penyelesaian Longgokan ini ialah struktur berbilang lapisan Bahagian atas mengandungi petak sepadan dengan klausa, bahagian tengah adalah petak sepadan dengan pembolehubah, dan bahagian bawah adalah petak sepadan dengan klausa.

Kami menggunakan contoh khusus untuk menerangkan pengurangan ini, dengan mengandaikan bahawa tika 3-SAT ialah 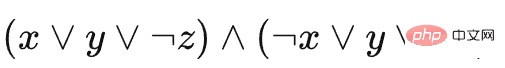. Kemudian contoh permainan biri-biri adalah seperti berikut (untuk menyatakan jenis dan situasi susun setiap blok, kami menggunakan pandangan sisi untuk memaparkan)

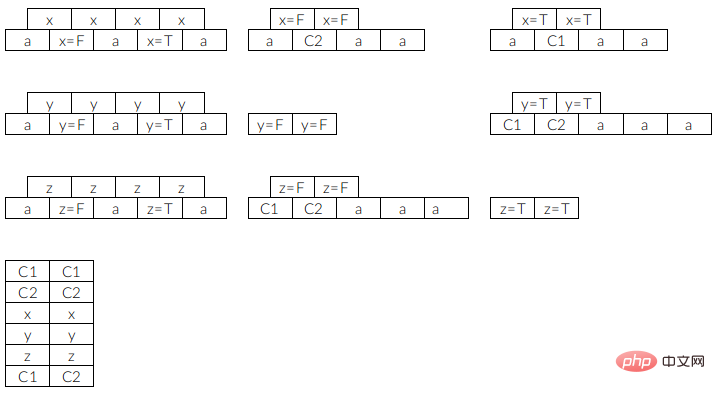
Antaranya, C1 mewakili 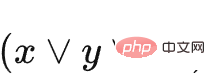, C2 mewakili 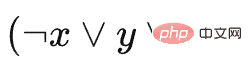, a ialah petak isi, dan petak a tidak menekan sebarang petak, jadi ia boleh dibiarkan sehingga akhir dan kemudian semua dihapuskan Tidak menjejaskan blok lain. Ambil perhatian bahawa bilangan slot yang kami tetapkan di sini ialah 3, yang bermaksud bahawa selepas memilih blok tertentu dan meletakkannya dalam slot, anda mesti menghapuskan blok jenis ini, jika tidak, permainan tidak akan diteruskan.

Jika formula boleh dipenuhi, maka blok boleh dihapuskan mengikut tugasan setiap pembolehubah apabila ia berpuas hati. Sebagai contoh, dengan mengandaikan bahawa xyz semuanya diberikan FALSE, maka kita akan menghapuskan tiga x, y, dan z paling kiri Dengan cara ini, petak dua lapisan kedua x=F, y=F, dan z=F akan dibuka kuncinya. dan kita boleh menghapuskannya. Semua blok x=F y=F z=F, kemudian satu blok C1 dan dua blok C2 akan dibuka, dan kemudian dengan timbunan blok pengesahan bawah, dua lapisan atas cerucuk pengesahan boleh dihapuskan , dan kemudian blok xyz pembolehubah tengah juga akan dibuka kunci Ia boleh dihapuskan serta-merta, dan pada akhirnya tiada had, semua blok boleh dihapuskan.

Sebaliknya, jika semua blok boleh dihapuskan (iaitu tahap boleh dilalui), maka formula boleh berpuas hati. Ambil perhatian bahawa jika blok xyz pembolehubah dalam timbunan pengesahan ingin dihapuskan, blok klausa C1 C2 atas mesti dihapuskan terlebih dahulu dan blok klausa dihadkan kepada blok tugasan, blok tugasan dihadkan kepada blok pembolehubah dan penempatan blok pembolehubah Kaedah peletakan menentukan bahawa apabila memberikan nilai kepada pembolehubah, setiap pembolehubah hanya boleh diberikan kepada salah satu daripada FALSE atau TRUE (khususnya, selepas menghapuskan sewenang-wenangnya 3 daripada 4 petak x pada permulaan permainan, petak x=F dan x=T Mesti ada satu yang tidak dibuka). Ini bermakna bahawa susunan blok disingkirkan membayangkan tugasan yang memenuhi formula.

Ini bermakna syarat yang perlu dan mencukupi untuk formula 3-SAT dipenuhi ialah contoh permainan Sheep Le Ge Sheep yang sepadan boleh diluluskan. Dan biri-biri daripada biri-biri jelas kepunyaan NP, kerana ia boleh ditentukan dalam masa polinomial sama ada urutan operasi boleh menghapuskan semua blok, jadi kami telah membuktikan proposisi berikut:

Proposisi: Dalam semua Di bawah syarat bahawa jenis blok yang disekat adalah pasti dan diketahui, permainan domba-le-biri yang digalakkan adalah NP-lengkap.

Dalam istilah bukan manusia, anda tidak mempunyai cara untuk mereka bentuk algoritma dengan kerumitan masa polinomial untuk menentukan sama ada mana-mana tahap am biri-biri mempunyai penyelesaian, melainkan P=NP ( Persamaan 4 aksara ini bernilai hadiah tanah dan $1 juta, jadi jangan duduk diam cuba membuktikan atau menafikannya). Dalam istilah manusia, walaupun jenis blok yang disekat adalah pasti dan diketahui, komputer masih (hampir) tidak dapat menentukan dengan cepat sama ada seekor biri-biri boleh melepasi tahap.

Atas ialah kandungan terperinci NP benar-benar retak biri-biri dan kehilangan biri-biri?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!