Pemprosesan imej Python: penapisan domain frekuensi, pengurangan hingar dan peningkatan imej

Pemprosesan imej telah menjadi sebahagian daripada kehidupan seharian kita, melibatkan pelbagai bidang seperti media sosial dan pengimejan perubatan. Imej yang diperoleh daripada kamera digital atau sumber lain seperti foto satelit dan imbasan perubatan mungkin memerlukan prapemprosesan untuk mengeluarkan atau meningkatkan bunyi. Penapisan domain frekuensi ialah penyelesaian yang mungkin yang boleh menghilangkan hingar sambil meningkatkan penajaman imej.

Fast Fourier Transform (FFT) ialah teknik matematik yang mengubah imej daripada domain spatial kepada domain frekuensi Ia merupakan alat utama untuk transformasi frekuensi dalam pemprosesan imej. Dengan memanfaatkan perwakilan domain frekuensi imej, kami boleh menganalisis imej dengan berkesan berdasarkan kandungan frekuensinya, dengan itu memudahkan penggunaan prosedur penapisan untuk mengeluarkan bunyi. Artikel ini akan membincangkan pelbagai peringkat yang terlibat dalam transformasi frekuensi imej daripada FFT kepada FFT songsang, digabungkan dengan penggunaan anjakan FFT dan anjakan FFT songsang.

Artikel ini menggunakan tiga perpustakaan Python, iaitu openCV, Numpy dan Matplotlib.

import cv2
 import numpy as np
 from matplotlib import pyplot as plt
 img = cv2.imread('sample.png',0) # Using 0 to read image in grayscale mode
 plt.imshow(img, cmap='gray')#cmap is used to specify imshow that the image is in greyscale
 plt.xticks([]), plt.yticks([])# remove tick marks
 plt.show()

1. ) ialah teknik matematik yang digunakan secara meluas yang membolehkan imej ditukar daripada domain spatial kepada domain frekuensi dan merupakan komponen asas transformasi frekuensi. Menggunakan analisis FFT, keberkalaan imej boleh diperoleh dan dibahagikan kepada komponen frekuensi yang berbeza untuk menghasilkan spektrum imej yang memaparkan amplitud dan fasa bagi setiap komponen frekuensi imej masing-masing.

f = np.fft.fft2(img)#the image 'img' is passed to np.fft.fft2() to compute its 2D Discrete Fourier transform f
 mag = 20*np.log(np.abs(f))
 plt.imshow(mag, cmap = 'gray') #cmap='gray' parameter to indicate that the image should be displayed in grayscale.
 plt.title('Magnitude Spectrum')
 plt.xticks([]), plt.yticks([])
 plt.show()

Kod di atas menggunakan np.abs() untuk mengira amplitud transformasi Fourier f, np. log () untuk menukar kepada skala logaritma, kemudian darab dengan 20 untuk mendapatkan amplitud dalam desibel. Ini dilakukan untuk menjadikan spektrum amplitud lebih mudah untuk divisualisasikan dan ditafsirkan.

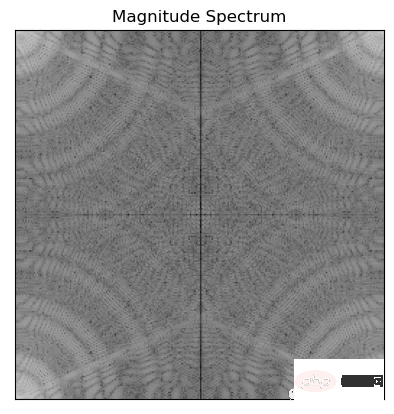
2. Anjakan FFT

Untuk menggunakan algoritma penapisan pada imej, anjakan FFT digunakan untuk memindahkan komponen frekuensi sifar imej ke tengah spektrum

Penapis laluan tinggi yang ideal ialah penapis yang panjang tidak terhingga dengan lebar jalur frekuensi tak terhingga dan tindak balas jalur laluan dan jalur henti yang ideal. Isyarat semua frekuensi dalam jalur laluannya dihantar sepenuhnya, manakala isyarat semua frekuensi dalam jalur hentinya ditindas sepenuhnya.

fshift = np.fft.fftshift(f)
 mag = 20*np.log(np.abs(fshift))
 plt.imshow(mag, cmap = 'gray')
 plt.title('Centered Spectrum'), plt.xticks([]), plt.yticks([])
 plt.show()

Dalam domain frekuensi, tindak balas frekuensi amplitud bagi penapis yang ideal ialah:

Dalam jalur laluan, tindak balas frekuensi amplitud ialah 1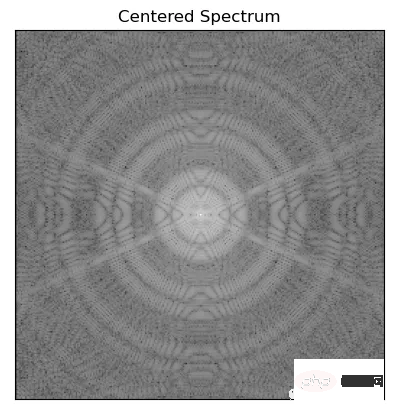

Dalam jalur henti, Tindak balas frekuensi amplitud ialah 0

Dalam domain masa, tindak balas impuls penapis ideal ialah:

Dalam jalur laluan, tindak balas impuls ialah jujukan fungsi impuls Unit tak terhingga

Dalam jalur henti, tindak balas impuls adalah sifar

• Memandangkan penapis ideal mempunyai lebar jalur tak terhingga dalam domain frekuensi, ia tidak boleh dilaksanakan dalam aplikasi praktikal . Penapis digital yang digunakan dalam amalan biasanya berdasarkan anggaran penapis ideal, jadi ia hanya Ideal.
• Penapis laluan tinggi Gaussian ialah penapis yang biasa digunakan dalam pemprosesan imej digital. Fungsinya adalah untuk mengekalkan maklumat terperinci frekuensi tinggi dalam imej dan menyekat isyarat frekuensi rendah. Penapis ini berdasarkan fungsi Gaussian dan mempunyai tindak balas frekuensi lancar yang boleh menyesuaikan diri dengan pelbagai butiran imej.

Tindak balas kekerapan penapis laluan tinggi Gaussian boleh dinyatakan sebagai:

H(u,v) = 1 - L(u,v)

• Di mana, L(u, v) ialah penapis laluan rendah, yang boleh diwakili oleh fungsi Gaussian. Tindak balas penapis laluan tinggi diperoleh dengan menolak tindak balas penapis laluan rendah daripada 1. Dalam amalan, tetapan parameter yang berbeza biasanya digunakan untuk melaraskan fungsi Gaussian untuk mencapai kesan penapisan yang berbeza.
• Imej berbentuk cakera digunakan untuk menentukan komponen frekuensi yang akan dikekalkan atau ditindas apabila Fourier mengubah imej. Dalam konteks ini, penapis ideal biasanya merujuk kepada penapis laluan rendah atau laluan tinggi yang ideal yang boleh dipilih dalam domain frekuensi untuk mengekalkan atau menyekat isyarat dalam julat frekuensi tertentu. Selepas menggunakan penapis ideal ini pada transformasi Fourier imej, dan kemudian melakukan transformasi songsang, imej yang diproses oleh penapis boleh diperolehi.

Kami tidak akan memperkenalkan butiran khusus, mari lihat kod terus:

Fungsi berikut adalah untuk menjana topeng bulat untuk penapis laluan tinggi dan laluan rendah yang ideal

Fungsi berikut menjana penapis laluan tinggi dan rendah Gaussian dengan topeng bulat yang diperlukan

Contoh penapisan

相乘过滤器和移位的图像得到过滤图像

为了获得具有所需频率响应的最终滤波图像，关键是在频域中对移位后的图像与滤波器进行逐点乘法。

这个过程将两个图像元素的对应像素相乘。例如，当应用低通滤波器时，我们将对移位的傅里叶变换图像与低通滤波器逐点相乘。

此操作抑制高频并保留低频，对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的，从而产生更清晰和更清晰的图像。

它使我们能够获得期望的频率响应，并在频域获得最终滤波图像。

4、乘法滤波器（Multiplying Filter）和平移后的图像（Shifted Image）

乘法滤波器是一种以像素值为权重的滤波器，它通过将滤波器的权重与图像的像素值相乘，来获得滤波后的像素值。具体地，假设乘法滤波器的权重为h(i,j)，图像的像素值为f(m,n)，那么滤波后的像素值g(x,y)可以表示为：

g(x,y) = ∑∑ f(m,n)h(x-m,y-n)

其中，∑∑表示对所有的(m,n)进行求和。

平移后的图像是指将图像进行平移操作后的结果。平移操作通常是指将图像的像素沿着x轴和y轴方向进行平移。平移后的图像与原始图像具有相同的大小和分辨率，但它们的像素位置发生了变化。在滤波操作中，平移后的图像可以用于与滤波器进行卷积运算，以实现滤波操作。

此操作抑制高频并保留低频，对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的，从而产生更清晰和更清晰的图像。

它使我们能够获得期望的频率响应，并在频域获得最终滤波图像。

fig, ax = plt.subplots()
 im = ax.imshow(np.log(1+np.abs(fftshifted_image * idealFilterLP(50,img.shape))), cmap='gray')
 ax.set_title('Filtered Image in Frequency Domain')
 ax.set_xticks([])
 ax.set_yticks([])
 
 fig.savefig('filtered image in freq domain.png', bbox_inches='tight')

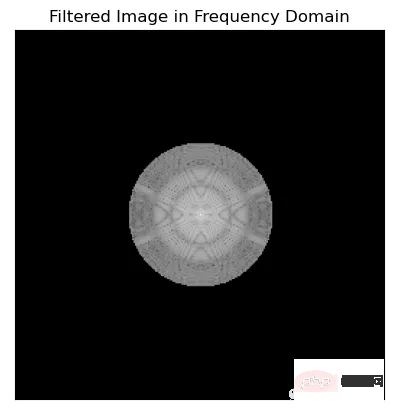
在可视化傅里叶频谱时，使用np.log(1+np.abs(x))和20*np.log(np.abs(x))之间的选择是个人喜好的问题，可以取决于具体的应用程序。

一般情况下会使用Np.log (1+np.abs(x))，因为它通过压缩数据的动态范围来帮助更清晰地可视化频谱。这是通过取数据绝对值的对数来实现的，并加上1以避免取零的对数。

而20*np.log(np.abs(x))将数据按20倍缩放，并对数据的绝对值取对数，这可以更容易地看到不同频率之间较小的幅度差异。但是它不会像np.log(1+np.abs(x))那样压缩数据的动态范围。

这两种方法都有各自的优点和缺点，最终取决于具体的应用程序和个人偏好。

5、逆FFT位移

在频域滤波后，我们需要将图像移回原始位置，然后应用逆FFT。为了实现这一点，需要使用逆FFT移位，它反转了前面执行的移位过程。

fig, ax = plt.subplots()
 im = ax.imshow(np.log(1+np.abs(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape)))), cmap='gray')
 ax.set_title('Filtered Image inverse fft shifted')
 ax.set_xticks([])
 ax.set_yticks([])
 
 fig.savefig('filtered image inverse fft shifted.png', bbox_inches='tight')

6、快速傅里叶逆变换(IFFT)

快速傅里叶逆变换(IFFT)是图像频率变换的最后一步。它用于将图像从频域传输回空间域。这一步的结果是在空间域中与原始图像相比，图像减少了噪声并提高了清晰度。

fig, ax = plt.subplots()
 im = ax.imshow(np.log(1+np.abs(np.fft.ifft2(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape))))), cmap='gray')
 ax.set_title('Final Filtered Image In Spatial Domain')
 ax.set_xticks([])
 ax.set_yticks([])
 
 fig.savefig('final filtered image.png', bbox_inches='tight')

总结

我们再把所有的操作串在一起显示，

函数绘制所有图像

def Freq_Trans(image, filter_used):
 img_in_freq_domain = np.fft.fft2(image)
 
 # Shift the zero-frequency component to the center of the frequency spectrum
 centered = np.fft.fftshift(img_in_freq_domain)
 
 # Multiply the filter with the centered spectrum
 filtered_image_in_freq_domain = centered * filter_used
 
 # Shift the zero-frequency component back to the top-left corner of the frequency spectrum
 inverse_fftshift_on_filtered_image = np.fft.ifftshift(filtered_image_in_freq_domain)
 
 # Apply the inverse Fourier transform to obtain the final filtered image
 final_filtered_image = np.fft.ifft2(inverse_fftshift_on_filtered_image)
 
 return img_in_freq_domain,centered,filter_used,filtered_image_in_freq_domain,inverse_fftshift_on_filtered_image,final_filtered_image

使用高通、低通理想滤波器和高斯滤波器的直径分别为50、100和150像素，展示它们对增强图像清晰度的影响。

fig, axs = plt.subplots(12, 7, figsize=(30, 60))
 
 filters = [(f, d) for f in [idealFilterLP, idealFilterHP, gaussianLP, gaussianHP] for d in [50, 100, 150]]
 
 for row, (filter_name, filter_diameter) in enumerate(filters):
 # Plot each filter output on a separate subplot
 result = Freq_Trans(img, filter_name(filter_diameter, img.shape))
 
 for col, title, img_array in zip(range(7),
["Original Image", "Spectrum", "Centered Spectrum", f"{filter_name.__name__} of Diameter {filter_diameter} px",
 f"Centered Spectrum multiplied by {filter_name.__name__}", "Decentralize", "Processed Image"],
[img, np.log(1+np.abs(result[0])), np.log(1+np.abs(result[1])), np.abs(result[2]), np.log(1+np.abs(result[3])),
np.log(1+np.abs(result[4])), np.abs(result[5])]):
 
 axs[row, col].imshow(img_array, cmap='gray')
 axs[row, col].set_title(title)
 
 plt.tight_layout()
 plt.savefig('all_processess.png', bbox_inches='tight')
 plt.show()

Dapat dilihat apabila menukar diameter topeng bulat, impak pada kejelasan imej akan berbeza. Apabila diameter bertambah, lebih banyak frekuensi ditindas, menghasilkan imej yang lebih lancar dengan butiran yang kurang. Mengurangkan diameter membolehkan lebih banyak frekuensi melaluinya, menghasilkan imej yang lebih tajam dan lebih terperinci. Untuk mencapai kesan yang diingini, adalah penting untuk memilih diameter yang betul, kerana menggunakan diameter yang terlalu kecil akan menghasilkan penapis yang tidak cukup berkesan, manakala menggunakan diameter yang terlalu besar akan menghasilkan terlalu banyak perincian. sedang hilang.

Secara umumnya, penapis Gaussian lebih biasa digunakan dalam tugas pemprosesan imej kerana kelicinan dan keteguhannya. Dalam sesetengah aplikasi, apabila potongan yang lebih tajam diperlukan, penapis yang ideal mungkin lebih sesuai.

Menggunakan FFT untuk mengubah suai kekerapan imej ialah kaedah yang berkesan untuk mengurangkan hingar dan meningkatkan ketajaman imej. Ini melibatkan penggunaan FFT untuk menukar imej kepada domain frekuensi, menggunakan teknik yang sesuai untuk menapis hingar dan menggunakan FFT songsang untuk menukar imej yang diubah suai kembali kepada domain spatial. Dengan memahami dan melaksanakan teknik ini, kami boleh meningkatkan kualiti imej untuk pelbagai aplikasi.

Atas ialah kandungan terperinci Pemprosesan imej Python: penapisan domain frekuensi, pengurangan hingar dan peningkatan imej. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!