selamat tinggal! Python gelung, vektorisasi adalah menakjubkan

Kami telah mempelajari tentang gelung dalam hampir semua bahasa pengaturcaraan. Jadi, secara lalai, setiap kali terdapat operasi berulang, kami mula melaksanakan gelung. Tetapi apabila kita berhadapan dengan banyak lelaran (berjuta-juta/berbilion baris), menggunakan gelung adalah sangat menyakitkan, dan anda mungkin terperangkap selama berjam-jam, hanya untuk menyedari kemudian bahawa ia tidak berfungsi. Di sinilah pelaksanaan vektorisasi dalam Python menjadi sangat kritikal.

Apakah itu vektorisasi?

Vektorisasi ialah teknik untuk melaksanakan operasi tatasusunan (NumPy) pada set data. Di sebalik tabir, ia beroperasi pada semua elemen tatasusunan atau siri sekali gus (tidak seperti gelung 'untuk', yang mengendalikan satu baris pada satu masa).

Dalam blog ini, kita akan melihat beberapa kes penggunaan di mana kita boleh menggantikan gelung Python dengan mudah dengan vektorisasi. Ini akan membantu anda menjimatkan masa dan menjadi lebih mahir dalam pengekodan.

Gunakan Kes 1: Mencari Jumlah Nombor

Mula-mula, mari kita lihat contoh asas mencari jumlah nombor dalam Python menggunakan gelung dan vektor.

Menggunakan gelung

import time 
start = time.time()

# 遍历之和
total = 0
# 遍历150万个数字
for item in range(0, 1500000):
total = total + item

print('sum is:' + str(total))
end = time.time()

print(end - start)

#1124999250000
#0.14 Seconds

Menggunakan vektorisasi

import numpy as np

start = time.time()

# 向量化和--使用numpy进行向量化
# np.range创建从0到1499999的数字序列
print(np.sum(np.arange(1500000)))

end = time.time()
print(end - start)

##1124999250000
##0.008 Seconds

Berbanding dengan lelaran menggunakan fungsi julat, The masa pelaksanaan vektorisasi adalah kira-kira 18 kali. Perbezaan ini menjadi lebih jelas apabila bekerja dengan Pandas DataFrame.

Kes Penggunaan 2: Operasi Matematik DataFrame

Dalam sains data, apabila bekerja dengan Pandas DataFrame, pembangun menggunakan gelung untuk mencipta lajur terbitan baharu untuk operasi matematik.

Dalam contoh di bawah, kita dapat melihat bahawa gelung boleh digantikan dengan mudah dengan vektorisasi dalam kes penggunaan sedemikian.

Buat DataFrame

DataFrame ialah data jadual dalam bentuk baris dan lajur.

Kami sedang mencipta DataFrame panda dengan 5 juta baris dan 4 lajur yang diisi dengan nilai rawak antara 0 dan 50.

import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randint(0, 50, 
size=(5000000, 4)),
columns=('a','b','c','d'))
df.shape
# (5000000, 5)
df.head()

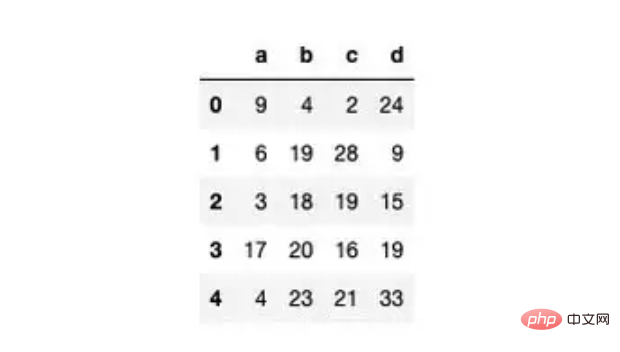
Kami akan mencipta 'nisbah' lajur baharu untuk mencari nisbah lajur 'd' dan 'c'.

Menggunakan gelung

import time 
start = time.time()

# Iterating through DataFrame using iterrows
for idx, row in df.iterrows():
# creating a new column 
df.at[idx,'ratio'] = 100 * (row["d"] / row["c"])
end = time.time()
print(end - start)
### 109 Seconds

Menggunakan vektorisasi

start = time.time()
df["ratio"] = 100 * (df["d"] / df["c"])

end = time.time()
print(end - start)
### 0.12 seconds

Kita dapat melihat bahawa DataFrame mempunyai Penambahbaikan yang jelas, pengvektoran hampir 1000 kali lebih pantas berbanding gelung dalam python.

Kes penggunaan 3: Pernyataan If-else pada DataFrame

Kami telah melaksanakan banyak operasi yang memerlukan kami menggunakan logik jenis "if-else". Kita boleh dengan mudah menggantikan logik ini dengan operasi vektor dalam python.

Sila lihat contoh di bawah untuk memahaminya dengan lebih baik (kami akan menggunakan DataFrame yang dibuat dalam use case 2).

Bayangkan bagaimana anda boleh mencipta lajur 'e' baharu berdasarkan beberapa syarat lajur 'a' yang keluar.

Gunakan gelung

import time 
start = time.time()

# Iterating through DataFrame using iterrows
for idx, row in df.iterrows():
if row.a == 0:
df.at[idx,'e'] = row.d
elif (row.a <= 25) & (row.a > 0):
df.at[idx,'e'] = (row.b)-(row.c)
else:
df.at[idx,'e'] = row.b + row.c

end = time.time()

print(end - start)
### Time taken: 177 seconds

Gunakan vektorisasi

start = time.time()
df['e'] = df['b'] + df['c']
df.loc[df['a'] <= 25, 'e'] = df['b'] -df['c']
df.loc[df['a']==0, 'e'] = df['d']end = time.time()
print(end - start)
## 0.28007707595825195 sec

dengan python dengan pernyataan if-else Berbanding dengan gelung, operasi bervektor adalah 600 kali lebih pantas daripada gelung.

Kes Penggunaan 4: Menyelesaikan Pembelajaran Mesin/Rangkaian Pembelajaran Mendalam

Pembelajaran mendalam memerlukan kita menyelesaikan berbilang persamaan kompleks dan untuk berjuta-juta dan berbilion-bilion baris persamaan. Menjalankan gelung dalam Python untuk menyelesaikan persamaan ini adalah sangat perlahan, di mana vektorisasi adalah penyelesaian terbaik.

Sebagai contoh, anda ingin mengira nilai y untuk berjuta-juta baris dalam persamaan regresi berbilang linear berikut.

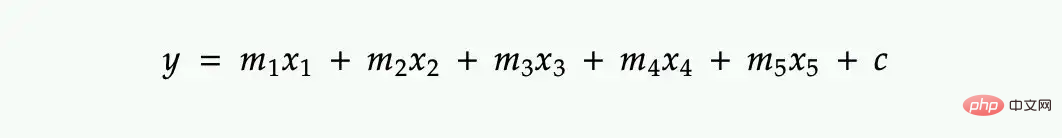
Kita boleh menggunakan vektorisasi dan bukannya gelung.

Nilai m1,m2,m3... ditentukan dengan menyelesaikan persamaan di atas menggunakan berjuta-juta nilai yang sepadan dengan x1,x2,x3... (untuk kesederhanaan, lihat satu sahaja Langkah pendaraban mudah)

Buat data

>>> import numpy as np
>>> # 设置 m 的初始值 
>>> m = np.random.rand(1,5)
array([[0.49976103, 0.33991827, 0.60596021, 0.78518515, 0.5540753]])
>>> # 500万行的输入值
>>> x = np.random.rand(5000000,5)

Gunakan gelung

import numpy as np
m = np.random.rand(1,5)
x = np.random.rand(5000000,5)

total = 0
tic = time.process_time()

for i in range(0,5000000):
total = 0
for j in range(0,5):
total = total + x[i][j]*m[0][j] 

zer[i] = total 

toc = time.process_time()
print ("Computation time = " + str((toc - tic)) + "seconds")

####Computation time = 28.228 seconds

Menggunakan vektorisasi

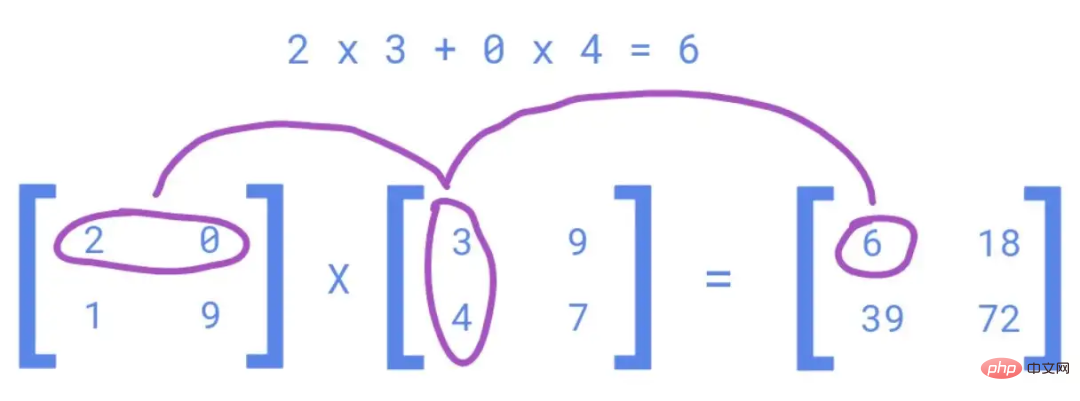
tic = time.process_time()

#dot product 
np.dot(x,m.T) 

toc = time.process_time()
print ("Computation time = " + str((toc - tic)) + "seconds")

####Computation time = 0.107 seconds

np.dot melaksanakan pendaraban matriks vektor di bahagian belakang. Ia 165 kali lebih pantas berbanding gelung dalam python.

Ditulis pada penghujung

Vektorisasi dalam Python adalah sangat pantas, dan apabila berurusan dengan set data yang sangat besar, anda disyorkan supaya mengutamakan vektorisasi berbanding gelung. Dengan cara ini, lama-kelamaan, anda secara beransur-ansur akan membiasakan diri untuk menulis kod mengikut idea vektorisasi.

Atas ialah kandungan terperinci selamat tinggal! Python gelung, vektorisasi adalah menakjubkan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!