 Peranti teknologi
Peranti teknologi AI
AI Penguraian matriks Poisson: Algoritma penguraian matriks yang menyelesaikan masalah permulaan sejuk sistem pengesyoran tanpa data
Penguraian matriks Poisson: Algoritma penguraian matriks yang menyelesaikan masalah permulaan sejuk sistem pengesyoran tanpa dataPenguraian matriks Poisson: Algoritma penguraian matriks yang menyelesaikan masalah permulaan sejuk sistem pengesyoran tanpa data
Pengarang |. Wang Hao
Penilai |. Dalam dekad yang lalu, industri Internet telah menghasilkan berjuta-juta versi berulang model sistem pengesyoran. Walaupun terdapat banyak model sistem pengesyoran yang dioptimumkan untuk senario yang berbeza, terdapat sangat sedikit model klasik. Penguraian matriks ialah algoritma sistem pengesyoran yang muncul pada masa awal bidang sistem pengesyoran dan menunjukkan keunggulannya dalam persaingan Netflix Ia juga merupakan algoritma sistem pengesyoran yang paling berjaya dalam sepuluh tahun yang lalu. Walaupun pada hari ini pada tahun 2023, bidang sistem pengesyoran telah lama dikuasai oleh pembelajaran mendalam, penguraian matriks masih digunakan secara meluas dalam proses penyelidikan dan pembangunan syarikat utama, dan masih terdapat ramai penyelidik saintifik yang bekerja pada algoritma berkaitan.

Masalah permulaan sejuk sistem pengesyoran adalah satu lagi kawasan penyelidikan yang telah menarik perhatian ramai pada tahun ini. Banyak idea pengamal untuk menyelesaikan sistem pengesyoran ialah pemindahan pembelajaran dan meta-pembelajaran. Walau bagaimanapun, idea ini mempunyai kelemahan yang membawa maut, iaitu ia memerlukan data dari bidang pengetahuan lain. Banyak syarikat tidak memenuhi syarat ini. Algoritma permulaan sejuk, yang benar-benar tidak memerlukan sebarang data, muncul selepas ZeroMat dicadangkan pada tahun 2021. Algoritma perwakilan termasuk ZeroMat dan DotMat yang disebutkan dalam bahagian sebelumnya. Algoritma penguraian matriks Poisson (PoissonMat) yang akan diperkenalkan dalam artikel ini ialah kertas kerja yang diterbitkan pada Persidangan Akademik Antarabangsa 2022 MLISE 2022. Nama kertas itu ialah PoissonMat: Pemfaktoran Matriks Ubahsuai menggunakan Taburan Poisson dan Menyelesaikan Masalah Permulaan Dingin tanpa Data Input (alamat muat turun kertas: https://arxiv.org/abs/2212.10460).
Kami mula-mula menyemak definisi MAP bagi Pemfaktoran Matriks Kebarangkalian:










Rajah 2 Percubaan perbandingan penguraian matriks Poisson pada Set Data LDOS-CoMoDa
Berdasarkan keputusan perbandingan eksperimen, kita boleh membuat kesimpulan berikut : Pemfaktoran matriks Poisson (PoissonMat) mengatasi algoritma lain dalam kedua-dua metrik ketepatan dan kesaksamaan. Apa yang patut dipuji ialah algoritma penguraian matriks Poisson tidak menggunakan sebarang data input dan merupakan algoritma pembelajaran sifar pukulan lengkap, yang menyelesaikan masalah permulaan sejuk dengan baik.
Akhirnya, penulis menjalankan eksperimen pada komputer riba rumah Lenovo dengan 16G RAM dan Intel Core i5 Algoritma berjalan dengan sangat pantas dan pelaksanaannya sangat mudah.
Algoritma pembelajaran sifar pukulan, yang bertujuan untuk menyelesaikan masalah permulaan dingin sistem pengesyoran, kini merupakan tempat liputan penyelidikan. Algoritma pembelajaran sifar pukulan sebenar yang tidak memerlukan sebarang data untuk menyelesaikan masalah pembelajaran pukulan sifar, bermula daripada algoritma ZeroMat pada 2021. Algoritma penguraian matriks Poisson (PoissonMat) yang diperkenalkan dalam artikel ini berprestasi lebih baik daripada ZeroMat dan algoritma seterusnya DotMat, dan kini merupakan salah satu algoritma terbaik dalam bidang ini. Memandangkan penyelidikan berkaitan masih di peringkat awal, kami berharap ia akan menarik perhatian dan perhatian majoriti pengamal sains dan teknologi.
Pengenalan kepada pengarang
Wang Hao, bekas ketua Makmal Kepintaran Buatan Funplus dan bekas ketua Jabatan Data Besar Hengchang Litong. Lulus dari Universiti Utah di Amerika Syarikat dengan ijazah sarjana muda (2008) dan ijazah sarjana (2010). Sambilan MBA daripada Universiti Perniagaan dan Ekonomi Antarabangsa (2016). Dalam sistem pengesyoran (kesaksamaan/pengesyoran berasaskan senario/permulaan dingin/kebolehtafsiran/pembelajaran kedudukan), grafik komputer (pemodelan geometri/visualisasi), pemprosesan bahasa semula jadi (aplikasi pelaksanaan dalam industri), kawalan risiko dan anti-penipuan ( Kewangan/perubatan) dan arah lain dengan pengalaman bertahun-tahun dan cerapan unik. Beliau mempunyai 12 tahun pengalaman R&D dan pengurusan teknologi dalam Internet (Douban, Baidu, Sina, NetEase, dll.), teknologi kewangan (Hengchang Litong) dan syarikat permainan (Funplus, dll.). Menerbitkan 30 kertas kerja dalam persidangan dan jurnal akademik antarabangsa, dan memenangi 3 persidangan antarabangsa Anugerah Kertas Terbaik/Anugerah Laporan Kertas Terbaik (Anugerah Kertas Terbaik IEEE SMI 2008/Anugerah Persembahan Lisan Terbaik ICBDT 2020/Anugerah Persembahan Lisan Terbaik ICISCAE 2021). Pingat Emas Pertandingan Serantau Gunung Rocky Amerika Utara ACM/ICPC 2006. Pingat Gangsa 2004 dalam Pertuturan Akhir Pertandingan Kemahiran Bahasa Inggeris Kolej Kebangsaan. Pada tahun 2003, beliau memenangi tempat pertama dalam Bahasa Inggeris dalam bidang sains dan kejuruteraan dalam Peperiksaan Masuk Kolej Jinan.
Atas ialah kandungan terperinci Penguraian matriks Poisson: Algoritma penguraian matriks yang menyelesaikan masalah permulaan sejuk sistem pengesyoran tanpa data. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Jurang kemahiran AI memperlahankan rantaian bekalanApr 26, 2025 am 11:13 AM
Jurang kemahiran AI memperlahankan rantaian bekalanApr 26, 2025 am 11:13 AMIstilah "tenaga kerja siap sedia" sering digunakan, tetapi apakah maksudnya dalam industri rantaian bekalan? Menurut Abe Eshkenazi, Ketua Pegawai Eksekutif Persatuan Pengurusan Rantaian Bekalan (ASCM), ia menandakan profesional yang mampu mengkritik
 Bagaimana satu syarikat secara senyap -senyap bekerja untuk mengubah AI selama -lamanyaApr 26, 2025 am 11:12 AM
Bagaimana satu syarikat secara senyap -senyap bekerja untuk mengubah AI selama -lamanyaApr 26, 2025 am 11:12 AMRevolusi AI yang terdesentralisasi secara senyap -senyap mendapat momentum. Jumaat ini di Austin, Texas, Sidang Kemuncak Endgame Bittensor menandakan momen penting, beralih ke desentralisasi AI (DEAI) dari teori kepada aplikasi praktikal. Tidak seperti iklan mewah
 NVIDIA Melepaskan Microservices Nemo Untuk Menyebarkan Pembangunan Agen AIApr 26, 2025 am 11:11 AM
NVIDIA Melepaskan Microservices Nemo Untuk Menyebarkan Pembangunan Agen AIApr 26, 2025 am 11:11 AMPerusahaan AI menghadapi cabaran integrasi data Penggunaan perusahaan AI menghadapi cabaran utama: sistem bangunan yang dapat mengekalkan ketepatan dan kepraktisan dengan terus belajar data perniagaan. Microservices NEMO menyelesaikan masalah ini dengan mewujudkan apa yang NVIDIA menggambarkan sebagai "Flywheel Data", yang membolehkan sistem AI tetap relevan melalui pendedahan berterusan kepada maklumat perusahaan dan interaksi pengguna. Toolkit yang baru dilancarkan ini mengandungi lima microservices utama: Nemo Customizer mengendalikan penalaan model bahasa yang besar dengan latihan yang lebih tinggi. NEMO Evaluator menyediakan penilaian ringkas model AI untuk tanda aras tersuai. Nemo Guardrails Melaksanakan Kawalan Keselamatan untuk mengekalkan pematuhan dan kesesuaian
 AI melukis gambar baru untuk masa depan seni dan reka bentukApr 26, 2025 am 11:10 AM
AI melukis gambar baru untuk masa depan seni dan reka bentukApr 26, 2025 am 11:10 AMAI: Masa Depan Seni dan Reka Bentuk Kecerdasan Buatan (AI) mengubah bidang seni dan reka bentuk dengan cara yang belum pernah terjadi sebelumnya, dan impaknya tidak lagi terhad kepada amatur, tetapi lebih mempengaruhi profesional. Skim karya seni dan reka bentuk yang dihasilkan oleh AI dengan cepat menggantikan imej dan pereka bahan tradisional dalam banyak aktiviti reka bentuk transaksional seperti pengiklanan, generasi imej media sosial dan reka bentuk web. Walau bagaimanapun, artis dan pereka profesional juga mendapati nilai praktikal AI. Mereka menggunakan AI sebagai alat tambahan untuk meneroka kemungkinan estetik baru, menggabungkan gaya yang berbeza, dan membuat kesan visual baru. AI membantu artis dan pereka mengautomasikan tugas berulang, mencadangkan elemen reka bentuk yang berbeza dan memberikan input kreatif. AI menyokong pemindahan gaya, iaitu menggunakan gaya gambar
 Bagaimana Zoom merevolusikan kerja dengan Agentic AI: Dari mesyuarat ke tonggakApr 26, 2025 am 11:09 AM
Bagaimana Zoom merevolusikan kerja dengan Agentic AI: Dari mesyuarat ke tonggakApr 26, 2025 am 11:09 AMZoom, yang pada mulanya dikenali untuk platform persidangan video, memimpin revolusi tempat kerja dengan penggunaan inovatif AIS AI. Perbualan baru -baru ini dengan CTO Zoom, XD Huang, mendedahkan penglihatan yang bercita -cita tinggi syarikat itu. Menentukan Agentic AI Huang d
 Ancaman eksistensi ke universitiApr 26, 2025 am 11:08 AM
Ancaman eksistensi ke universitiApr 26, 2025 am 11:08 AMAdakah AI akan merevolusikan pendidikan? Soalan ini mendorong refleksi serius di kalangan pendidik dan pihak berkepentingan. Penyepaduan AI ke dalam pendidikan memberikan peluang dan cabaran. Sebagai Matthew Lynch dari Nota Edvocate Tech, Universit
 Prototaip: saintis Amerika mencari pekerjaan di luar negaraApr 26, 2025 am 11:07 AM
Prototaip: saintis Amerika mencari pekerjaan di luar negaraApr 26, 2025 am 11:07 AMPembangunan penyelidikan dan teknologi saintifik di Amerika Syarikat mungkin menghadapi cabaran, mungkin disebabkan oleh pemotongan anggaran. Menurut Alam, bilangan saintis Amerika yang memohon pekerjaan di luar negara meningkat sebanyak 32% dari Januari hingga Mac 2025 berbanding dengan tempoh yang sama pada tahun 2024. Pungutan sebelumnya menunjukkan bahawa 75% penyelidik yang ditinjau sedang mempertimbangkan untuk mencari pekerjaan di Eropah dan Kanada. Beratus-ratus geran NIH dan NSF telah ditamatkan dalam beberapa bulan yang lalu, dengan geran baru NIH turun kira-kira $ 2.3 bilion tahun ini, setitik hampir satu pertiga. Cadangan belanjawan yang bocor menunjukkan bahawa pentadbiran Trump sedang mempertimbangkan untuk memotong belanjawan secara mendadak untuk institusi saintifik, dengan kemungkinan pengurangan sehingga 50%. Kegawatan dalam bidang penyelidikan asas juga telah menjejaskan salah satu kelebihan utama Amerika Syarikat: menarik bakat luar negara. 35
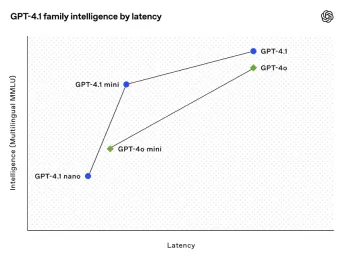 Semua Mengenai Keluarga GPT 4.1 Terbuka AI - Analytics VidhyaApr 26, 2025 am 10:19 AM
Semua Mengenai Keluarga GPT 4.1 Terbuka AI - Analytics VidhyaApr 26, 2025 am 10:19 AMOpenAI melancarkan siri GPT-4.1 yang kuat: keluarga tiga model bahasa lanjutan yang direka untuk aplikasi dunia nyata. Lompat penting ini menawarkan masa tindak balas yang lebih cepat, pemahaman yang lebih baik, dan kos yang dikurangkan secara drastik berbanding t


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Inggeris
Disyorkan: Versi Win, menyokong gesaan kod!

mPDF
mPDF ialah perpustakaan PHP yang boleh menjana fail PDF daripada HTML yang dikodkan UTF-8. Pengarang asal, Ian Back, menulis mPDF untuk mengeluarkan fail PDF "dengan cepat" dari tapak webnya dan mengendalikan bahasa yang berbeza. Ia lebih perlahan dan menghasilkan fail yang lebih besar apabila menggunakan fon Unicode daripada skrip asal seperti HTML2FPDF, tetapi menyokong gaya CSS dsb. dan mempunyai banyak peningkatan. Menyokong hampir semua bahasa, termasuk RTL (Arab dan Ibrani) dan CJK (Cina, Jepun dan Korea). Menyokong elemen peringkat blok bersarang (seperti P, DIV),

EditPlus versi Cina retak
Saiz kecil, penyerlahan sintaks, tidak menyokong fungsi gesaan kod

Penyesuai Pelayan SAP NetWeaver untuk Eclipse
Integrasikan Eclipse dengan pelayan aplikasi SAP NetWeaver.






