Keperluan pembelajaran mesin: Bagaimana untuk mengelakkan overfitting?

Sebenarnya, intipati regularisasi adalah sangat mudah Ia adalah satu cara atau operasi yang mengenakan sekatan atau kekangan apriori terhadap masalah tertentu untuk mencapai tujuan tertentu. Tujuan menggunakan regularization dalam algoritma adalah untuk mengelakkan model daripada overfitting. Apabila bercakap mengenai penyelarasan, ramai pelajar mungkin segera memikirkan norma L1 dan norma L2 yang biasa digunakan Sebelum merumuskan, mari kita lihat apa itu norma LP?

Norma LP

Norma boleh difahami dengan mudah sebagai digunakan untuk mewakili jarak dalam ruang vektor, dan takrifan jarak adalah sangat abstrak. Ia boleh dipanggil selagi ia memenuhi bukan negatif , ketaksamaan refleksif dan segi tiga Ia adalah jarak.

Norma LP bukan norma, tetapi satu set norma, yang ditakrifkan seperti berikut:

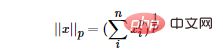
Julat p ialah [1,∞) . p tidak ditakrifkan sebagai norma dalam julat (0,1) kerana ia melanggar ketaksamaan segitiga.

Mengikut perubahan pp, norma juga berubah secara berbeza Meminjam gambar rajah perubahan klasik norma P seperti berikut:

Gambar di atas menunjukkan Ia. menunjukkan perubahan bola unit apabila p berubah daripada 0 kepada infiniti positif. Bola unit yang ditakrifkan di bawah norma P ialah set cembung, tetapi apabila 0

Maka persoalannya, apakah norma L0? Norma L0 mewakili bilangan unsur bukan sifar dalam vektor, dinyatakan seperti berikut:

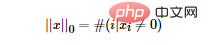
Kita boleh mencari ciri jarang yang paling kurang optimum dengan meminimumkan item L0. Tetapi malangnya, masalah pengoptimuman norma L0 adalah masalah keras NP (norma L0 juga bukan cembung). Oleh itu, dalam aplikasi praktikal, kami sering melakukan kelonggaran cembung L0 Secara teorinya terbukti bahawa norma L1 adalah penghampiran cembung optimum norma L0, jadi norma L1 biasanya digunakan dan bukannya mengoptimumkan norma L0 secara langsung.

norma L1

Mengikut takrifan norma LP kita boleh dengan mudah mendapatkan bentuk matematik norma L1:

Lulus Seperti Boleh dilihat daripada formula di atas, norma L1 ialah jumlah nilai mutlak setiap elemen vektor, juga dikenali sebagai "operator regularization jarang" (Lasso regularization). Jadi persoalannya, mengapa kita mahu sparsifikasi? Sparsifikasi mempunyai banyak faedah, dua yang paling langsung ialah:

• Pemilihan ciri
• Kebolehtafsiran

Norma L2

Norma L2 adalah yang paling biasa. Ia adalah jarak Euclidean Formulanya adalah seperti berikut:

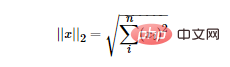
Norma L2 mempunyai banyak nama. Regresi Ridge), sesetengah orang juga memanggilnya "Reput Berat". Menggunakan norma L2 sebagai istilah regularisasi boleh mendapatkan penyelesaian padat, iaitu, parameter ww yang sepadan dengan setiap ciri adalah sangat kecil, hampir dengan 0 tetapi bukan 0 di samping itu, norma L2 sebagai istilah regularisasi boleh menghalang model daripada memenuhi set latihan Terlalu banyak kerumitan membawa kepada overfitting, dengan itu meningkatkan keupayaan generalisasi model.

Perbezaan antara norma L1 dan norma L2

Memperkenalkan rajah klasik PRML untuk menggambarkan perbezaan antara norma L1 dan L2, seperti ditunjukkan dalam rajah berikut:

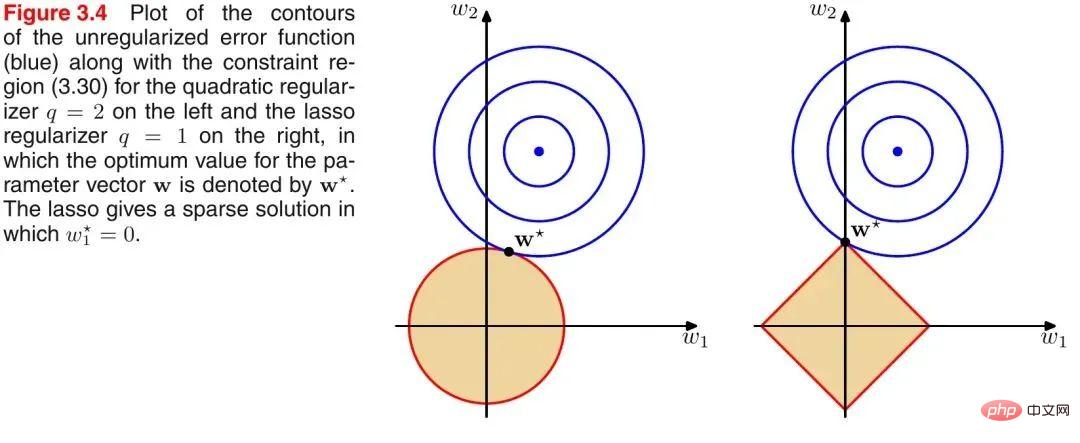
Seperti yang ditunjukkan dalam gambar di atas, bulatan biru mewakili julat penyelesaian masalah yang mungkin, dan bulatan oren mewakili julat penyelesaian yang mungkin bagi istilah biasa. Keseluruhan fungsi objektif (masalah asal + istilah biasa) mempunyai penyelesaian jika dan hanya jika dua julat penyelesaian adalah tangen. Ia boleh dilihat dengan mudah daripada rajah di atas bahawa oleh kerana julat penyelesaian norma L2 ialah bulatan, titik tangen berkemungkinan besar bukan pada paksi koordinat, dan kerana norma L1 ialah rombus (bucunya cembung), titik tangennya. Titik tangen lebih berkemungkinan berada pada paksi koordinat, dan titik pada paksi koordinat mempunyai ciri bahawa hanya satu komponen koordinat bukan sifar, dan komponen koordinat yang lain adalah sifar, iaitu, ia jarang. Oleh itu, terdapat kesimpulan berikut: Norma L1 boleh membawa kepada penyelesaian yang jarang, dan norma L2 boleh membawa kepada penyelesaian padat.

Dari perspektif terdahulu Bayesian, apabila melatih model, tidak cukup untuk bergantung semata-mata pada set data latihan semasa Untuk mencapai keupayaan generalisasi yang lebih baik, selalunya perlu menambah istilah terdahulu, dan istilah biasa bersamaan dengan menambah priori.

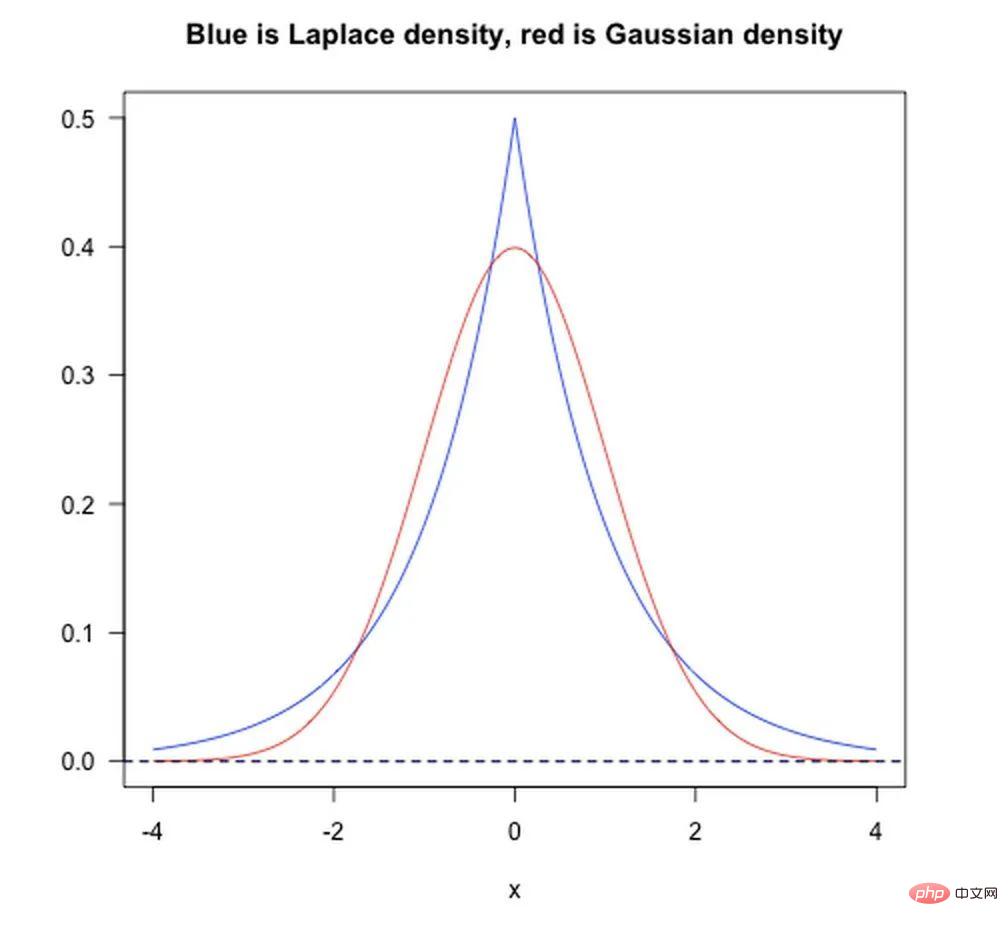
• Norma L1 adalah bersamaan dengan menambahkan sebelumnya Laplacean
• Norma L2 adalah bersamaan dengan menambahkan sebelumnya Gaussian.

Seperti yang ditunjukkan dalam rajah di bawah:

Keciciran

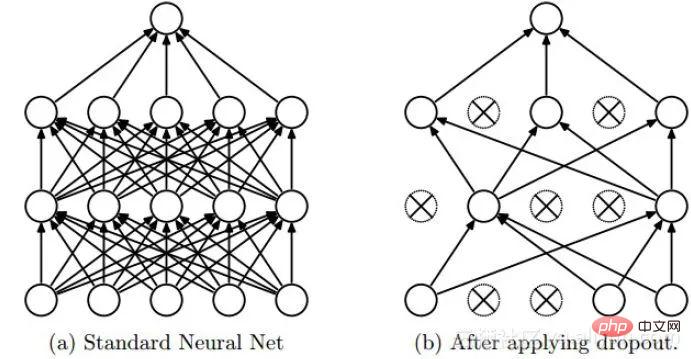
Keciciran ialah kaedah penyelarasan yang sering digunakan dalam pembelajaran mendalam. Pendekatannya boleh difahami dengan mudah sebagai membuang beberapa neuron dengan kebarangkalian p semasa proses latihan DNN, iaitu, output neuron yang dibuang ialah 0. Keciciran boleh dibuat seketika seperti yang ditunjukkan dalam rajah di bawah:

Kami secara intuitif boleh memahami kesan regularisasi Keciciran dari dua aspek:

• Operasi kehilangan neuron secara rawak semasa setiap pusingan latihan Keciciran adalah bersamaan dengan purata berbilang DNN, jadi ia mempunyai kesan pengundian apabila digunakan untuk ramalan.
• Kurangkan penyesuaian bersama kompleks antara neuron. Apabila neuron lapisan tersembunyi dipadamkan secara rawak, rangkaian yang disambungkan sepenuhnya menjadi jarang pada tahap tertentu, sekali gus mengurangkan kesan sinergistik ciri yang berbeza dengan berkesan. Dalam erti kata lain, beberapa ciri mungkin bergantung pada tindakan bersama nod tersembunyi dengan perhubungan tetap, dan melalui Dropout, ia secara berkesan mengatur keadaan di mana ciri tertentu berkesan hanya dengan kehadiran ciri lain, meningkatkan keteguhan rangkaian saraf seks.

Penormalan Kelompok

Penormalan Kelompok ialah kaedah penormalan, terutamanya digunakan untuk mempercepatkan penumpuan rangkaian, tetapi ia juga mempunyai tahap kesan penormalan tertentu.

Berikut ialah rujukan kepada penjelasan anjakan kovariat dalam jawapan Zhihu Dr. Wei Xiushen.

Nota: Kandungan berikut dipetik daripada jawapan Zhihu Dr. Wei Xiushen Semua orang tahu bahawa andaian klasik dalam pembelajaran mesin statistik ialah “pengagihan data ruang sumber (domain sumber) dan ruang sasaran (domain sasaran). ” (pengedaran) adalah konsisten”. Jika ia tidak konsisten, maka masalah pembelajaran mesin baharu timbul, seperti pembelajaran pemindahan/penyesuaian domain, dsb. Anjakan kovariat ialah masalah cawangan di bawah andaian pengedaran tidak konsisten Ini bermakna kebarangkalian bersyarat bagi ruang sumber dan ruang sasaran adalah konsisten, tetapi kebarangkalian marginalnya adalah berbeza. Jika anda memikirkannya dengan teliti, anda akan mendapati bahawa sesungguhnya, untuk output setiap lapisan rangkaian saraf, kerana mereka telah menjalani operasi intra-lapisan, pengedarannya jelas berbeza daripada pengedaran isyarat input yang sepadan bagi setiap lapisan, dan perbezaan akan meningkat apabila kedalaman rangkaian bertambah besar, tetapi label sampel yang mereka boleh "tunjukkan" kekal tidak berubah, yang memenuhi definisi anjakan kovariat.

Idea asas BN sebenarnya agak intuitif, kerana nilai input pengaktifan rangkaian saraf sebelum transformasi tak linear (X=WU+B, U ialah input) secara beransur-ansur beralih apabila kedalaman rangkaian mendalam. Atau berubah (iaitu anjakan kovariat yang disebutkan di atas). Sebab mengapa latihan bertumpu perlahan-lahan adalah kerana taburan keseluruhan secara beransur-ansur menghampiri had atas dan bawah julat nilai fungsi tak linear (untuk fungsi Sigmoid, ini bermakna nilai input pengaktifan X=WU+B ialah negatif besar atau nilai positif ), jadi ini menyebabkan kecerunan rangkaian saraf peringkat rendah hilang semasa perambatan belakang, yang merupakan sebab penting mengapa latihan rangkaian saraf dalam menumpu lebih dan lebih perlahan. BN menggunakan kaedah penyeragaman tertentu untuk memaksa pengagihan nilai input mana-mana neuron dalam setiap lapisan rangkaian saraf kembali kepada taburan normal piawai dengan min 0 dan varians 1, untuk mengelakkan masalah penyebaran kecerunan yang disebabkan oleh fungsi pengaktifan. Jadi daripada mengatakan bahawa peranan BN adalah untuk mengurangkan anjakan kovariat, adalah lebih baik untuk mengatakan bahawa BN boleh mengurangkan masalah penyebaran kecerunan.

Normalization, Standardization & Regularization

Kami telah menyebut regularization sebelum ini, di sini kami secara ringkas menyebut normalization dan standardization. Normalisasi: Matlamat normalisasi adalah untuk mencari hubungan pemetaan tertentu untuk memetakan data asal kepada selang [a, b]. Secara amnya, a dan b akan mengambil gabungan [−1,1], [0,1]. Secara umumnya terdapat dua senario aplikasi:

• Tukar nombor kepada perpuluhan antara (0, 1)
• Tukar nombor dimensi kepada nombor tanpa dimensi

Penormalan min-maks yang biasa digunakan:

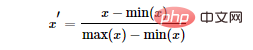
Penstandardan: Gunakan teorem nombor besar untuk mengubah data menjadi taburan normal piawai Formula penyeragaman ialah:

Perbezaan antara normalisasi dan penyeragaman:

Kita boleh menerangkannya secara ringkas seperti ini: penskalaan ternormal "diratakan" kepada selang (hanya ditentukan oleh nilai ekstrem), manakala penskalaan ternormal adalah Ia lebih "anjal " dan "dinamik" dan mempunyai banyak kaitan dengan pengedaran sampel keseluruhan. Nota:

• Penormalan: Penskalaan hanya berkaitan dengan perbezaan antara nilai maksimum dan minimum.
• Penstandardan: Penskalaan berkaitan dengan setiap titik dan dicerminkan oleh varians. Bezakan ini dengan normalisasi, di mana semua titik data menyumbang (melalui min dan sisihan piawai).

Mengapa penyeragaman dan penormalan?

• Tingkatkan ketepatan model: Selepas penormalan, ciri antara dimensi berbeza boleh dibandingkan secara numerik, yang boleh meningkatkan ketepatan pengelas dengan banyak.
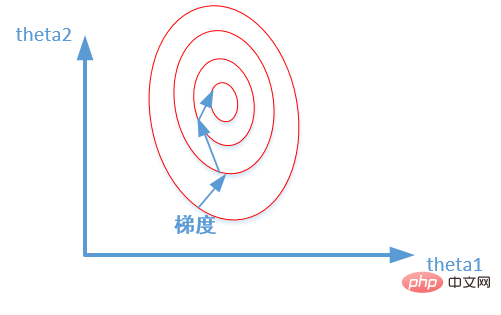
• Mempercepatkan penumpuan model: Selepas penyeragaman, proses pengoptimuman penyelesaian optimum jelas akan menjadi lebih lancar, menjadikannya lebih mudah untuk menumpu dengan betul kepada penyelesaian optimum. Seperti yang ditunjukkan dalam gambar di bawah:

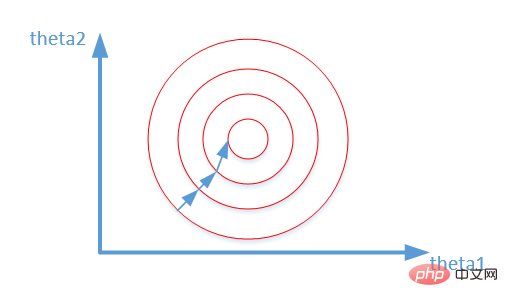
Atas ialah kandungan terperinci Keperluan pembelajaran mesin: Bagaimana untuk mengelakkan overfitting?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!