Rumah >Peranti teknologi >AI >Perbincangan ringkas tentang algoritma pembenaman graf
Perbincangan ringkas tentang algoritma pembenaman graf
- 王林ke hadapan
- 2023-04-12 17:52:062631semak imbas

Bahagian 01
● Apakah itu pembenaman imej ●
Pembenaman graf ialah proses memetakan data struktur graf ke dalam vektor tumpat berdimensi rendah Pada masa yang sama, nod dengan struktur topologi yang serupa atau atribut rapat dalam graf asal juga berada dalam kedudukan yang hampir ruang vektor, yang boleh dengan mudah Ia menyelesaikan masalah kesukaran dengan cekap memasukkan data berstruktur graf ke dalam algoritma pembelajaran mesin.
Untuk perwakilan dan penyimpanan graf, cara paling mudah untuk difikirkan ialah menggunakan matriks bersebelahan. Nomborkan setiap nod dalam graf untuk membina matriks  , dengan
, dengan 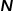 mewakili graf Bilangan nod . Sama ada mana-mana dua nod dalam graf disambungkan oleh tepi menentukan nilai kedudukan yang sepadan dalam matriks bersebelahan Kaedah perwakilan ini sangat mudah difahami dan intuitif, tetapi ia sangat tidak cekap. Oleh kerana graf dalam senario kehidupan sebenar mungkin mengandungi ribuan atau lebih banyak nod, dan kebanyakan nod tidak disambungkan dengan tepi, ini akan menyebabkan matriks bersebelahan yang terhasil menjadi sangat jarang. Menggunakan matriks bersebelahan untuk mewakili dan menyimpan graf memerlukan kos pengiraan dan ruang yang tinggi, manakala algoritma pembenaman graf boleh menyelesaikan masalah analisis graf dengan cekap.
mewakili graf Bilangan nod . Sama ada mana-mana dua nod dalam graf disambungkan oleh tepi menentukan nilai kedudukan yang sepadan dalam matriks bersebelahan Kaedah perwakilan ini sangat mudah difahami dan intuitif, tetapi ia sangat tidak cekap. Oleh kerana graf dalam senario kehidupan sebenar mungkin mengandungi ribuan atau lebih banyak nod, dan kebanyakan nod tidak disambungkan dengan tepi, ini akan menyebabkan matriks bersebelahan yang terhasil menjadi sangat jarang. Menggunakan matriks bersebelahan untuk mewakili dan menyimpan graf memerlukan kos pengiraan dan ruang yang tinggi, manakala algoritma pembenaman graf boleh menyelesaikan masalah analisis graf dengan cekap.
Bahagian 02
● Konsep Asas ●
Konsep 1 Gambar:
Graf diwakili sebagai 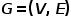 , dengan
, dengan 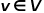 mewakili nod, dan
mewakili nod, dan 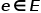 Mewakili kelebihan.
Mewakili kelebihan. 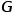 dengan fungsi pemetaan jenis nod
dengan fungsi pemetaan jenis nod 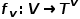 dan fungsi pemetaan jenis tepi
dan fungsi pemetaan jenis tepi 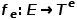 dikaitkan.
dikaitkan. 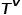 mewakili set jenis nod dan
mewakili set jenis nod dan 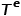 mewakili set jenis tepi.
mewakili set jenis tepi.
Konsep 2 diagram isomorfik:
Gambar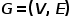 , di mana
, di mana 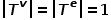 . Maksudnya, semua nod tergolong dalam satu jenis dan semua tepi tergolong dalam satu jenis Contohnya, graf hubungan perhatian pengguna dalam rangkaian sosial hanya mempunyai satu jenis nod, pengguna dan satu jenis tepi, hubungan perhatian.
. Maksudnya, semua nod tergolong dalam satu jenis dan semua tepi tergolong dalam satu jenis Contohnya, graf hubungan perhatian pengguna dalam rangkaian sosial hanya mempunyai satu jenis nod, pengguna dan satu jenis tepi, hubungan perhatian.
Konsep 3 Graf Heterogen:
Graf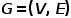 , di mana
, di mana 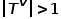 atau
atau 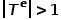 . Maksudnya, terdapat lebih daripada satu jenis nod atau jenis tepi Contohnya, dalam struktur graf dalam rangkaian akademik, terdapat berbilang jenis nod seperti kertas kerja, pengarang, dan perhubungan tepi termasuk hubungan kreatif antara pengarang dan kertas kerja, kertas kerja dan persidangan Hubungan penerbitan antara mereka, hubungan petikan antara kertas kerja, dll.
. Maksudnya, terdapat lebih daripada satu jenis nod atau jenis tepi Contohnya, dalam struktur graf dalam rangkaian akademik, terdapat berbilang jenis nod seperti kertas kerja, pengarang, dan perhubungan tepi termasuk hubungan kreatif antara pengarang dan kertas kerja, kertas kerja dan persidangan Hubungan penerbitan antara mereka, hubungan petikan antara kertas kerja, dll.
Konsep 4 Persamaan urutan pertama:
Jika berat tepi yang menyambungkan dua nod lebih besar, persamaan tertib pertama antara keduanya adalah lebih besar. Persamaan tertib pertama antara nod 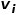 dan nod
dan nod 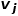 dinyatakan sebagai
dinyatakan sebagai 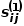 , terdapat
, terdapat 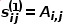 , di mana
, di mana 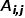 ialah nod antara 🎜>
ialah nod antara 🎜>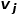 dan nod
dan nod  .
.
Konsep 5 Persamaan tertib kedua:
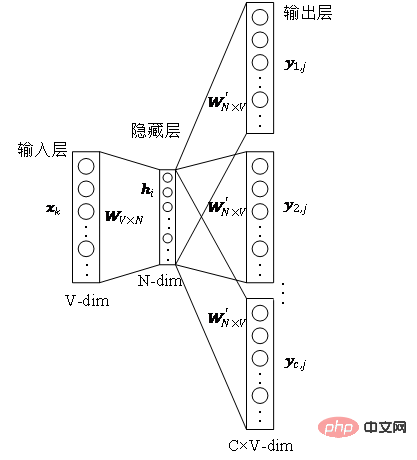
Jika dua nod bersebelahan dengan rangkaian Semakin serupa struktur, semakin besar persamaan tertib kedua di antara mereka. Persamaan tertib kedua antara nod Rajah 1 Diagram skematik persamaan tertib kedua Pembenaman Rajah 6: Memandangkan graf input dan dimensi benam yang dipratakrif, pembenaman graf adalah untuk menukar graf kepada ruang dimensi sambil mengekalkan sifat graf sebanyak mungkin. Bergantung pada persamaan tertib pertama atau persamaan tertib lebih tinggi untuk mengukur tahap pemeliharaan atribut graf, menggunakan vektor dimensi atau set Bahagian 03 ● Pengkelasan algoritma pembenaman grafik ● Dalam beberapa dekad yang lalu, penyelidik telah mencadangkan banyak algoritma yang sangat baik, yang telah terbukti mempunyai kesan ketara dalam rangkaian sosial, rangkaian komunikasi dan senario lain. Industri biasanya membahagikan algoritma pembenaman graf ini ke dalam tiga kategori berikut berdasarkan perbezaan dalam butiran keluaran: (1) Pembenaman nod Pembenaman nod ialah jenis yang paling biasa setiap nod dalam graf diwakili oleh vektor dalam ruang berdimensi rendah. Apabila perlu untuk menganalisis nod dalam graf dan kemudian melaksanakan tugas seperti pengelasan nod atau pengelompokan nod, pembenaman nod biasanya dipilih. (2) Pembenaman tepi Gunakan vektor untuk memetakan graf dalam dimensi rendah ruang Mewakili setiap tepi dalam . Tepi terdiri daripada sepasang nod dan biasanya mewakili hubungan pasangan nod. Pembenaman tepi sesuai apabila anda perlu menganalisis tepi dalam graf dan melaksanakan tugas seperti ramalan hubungan graf pengetahuan atau ramalan pautan. (3) Pembenaman graf menggunakan vektor untuk membenamkan keseluruhan perwakilan A ialah diwakili oleh gambar rajah, biasanya gambar rajah kecil seperti molekul atau protein. Mewakili graf sebagai vektor memudahkan pengiraan persamaan antara graf yang berbeza, dengan itu menyelesaikan masalah pengelasan graf. Keperluan tugas yang berbeza menentukan algoritma pembenaman graf yang dipilih Atas sebab ruang, algoritma DeepWalk dan algoritma Node2Vec dalam pembenaman nod dipetik di sini untuk membandingkan kajian terperinci. Bahagian 04 ● Algoritma pemasukan graf klasik ● 1. Algoritma DeepWalk Diinspirasikan oleh idea Word2vec dalam bidang pemprosesan bahasa semula jadi, Perozzi et al. Dalam model vektor perwakilan nod, hubungan kejadian bersama antara nod dianalogikan dengan hubungan kejadian bersama antara perkataan dalam korpus, dan algoritma DeepWalk dicadangkan. Urutan nod jiran nod dalam graf dikumpul melalui jalan rawak, yang bersamaan dengan korpus konteks nod, dan dengan itu boleh menyelesaikan masalah mengekstrak hubungan kejadian bersama antara nod dalam graf. Tetapkan panjang dan titik permulaan urutan nod terlebih dahulu Strategi berjalan secara rawak akan membimbing cara menentukan nod berjalan seterusnya di antara nod jiran Ulangi langkah ini untuk mendapatkan urutan yang memenuhi syarat Rajah berjalan secara rawak 2. Tunjukkan. Rajah 2 Gambarajah skematik berjalan rawak Sepadan dengan perkataan dalam word2vec algoritma sebagai Untuk nod Untuk mengetahui lebih lanjut perwakilan ciri terpendam nod, algoritma DeepWalk memperkenalkan fungsi pemetaan Pengiraan kebarangkalian juga perlu merujuk kepada model langkau-gram dalam algoritma word2vec. Seperti yang ditunjukkan dalam Rajah 3, model skip-gram mengandungi dua matriks utama, satu ialah matriks vektor kata tengah Dalam proses berjalan rawak, hubungan urutan antara nod dalam jujukan pensampelan tidak dipertimbangkan, yang boleh menjadi lebih baik Ia mencerminkan hubungan kedekatan nod dengan berkesan dan mengurangkan kos pengiraan. Rajah 3 Langkau-gram rajah model Algoritma 2.Node2Vec Berdasarkan algoritma DeepWalk, penyelidik Grover A dan Leskovec J mencadangkan algoritma Node2Vec. Algoritma Node2Vec mengoptimumkan proses menjana jujukan nod melalui jalan rawak dalam algoritma DeepWalk, mentakrifkan parameter di mana Rajah 4 Node2Vec rajah strategi berjalan rawak Strategi berjalan rawak Node2Vec dikawal berdasarkan dua parameter, seperti yang ditunjukkan dalam Rajah 4. Andaikan bahawa nod v dicapai melalui tepi Apabila sampel berjalan dari nod (1) Apabila (2) Apabila (3) Apabila Dengan kata lain, parameter Bahagian 05 ● Ringkasan ● Dengan perkembangan pesat teknologi maklumat, persekitaran rangkaian menjadi semakin kompleks, dan serangan rangkaian kerap berlaku Antaranya, serangan APT sangat berleluasa, yang merupakan isu keselamatan yang perlu dibayar oleh perusahaan perhatian kepada. Sebenarnya, rangkaian, persekitaran asas di mana serangan APT berlaku, itu sendiri adalah struktur rangkaian yang terdiri daripada komputer dan unsur-unsur lain Tidak sukar untuk memikirkan menggunakan struktur data graf untuk menyatakan hubungan antara unsur-unsur ini, dan kemudian mengubahnya masalah pengesanan serangan ke dalam tugas pengelasan Nod, tepi atau subgraf dalam graf. Pembenaman graf ialah isu yang kaya dengan ruang penyelidikan yang hebat Bagaimana untuk meningkatkan kecekapan latihan model, memperbaharui kaedah pembinaan model, dan menggunakan idea pembenaman graf untuk lebih banyak amalan pengeluaran. Rujukan [1]Xu M. Memahami kaedah pembenaman graf dan aplikasinya [J]. Semakan SIAM, 2021, 63(4): 825-853. [2]Cai H, Zheng V W, Chang K C C tinjauan pembenaman graf: Masalah, teknik dan aplikasi[J]. Transaksi IEEE mengenai Pengetahuan dan Kejuruteraan Data, 2018, 30(9): 1616-1637. [3]Goyal P, Ferrara E. Teknik pembenaman graf, aplikasi dan prestasi: Satu tinjauan[J].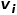 dan nod
dan nod 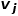
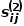 ialah kejiranan
ialah kejiranan 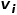 Persamaan antara kejiranan
Persamaan antara kejiranan 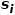 daripada 🎜>. Seperti yang ditunjukkan dalam Rajah 1, kerana terdapat tepi yang menghubungkan nod f dan nod g, nod f dan nod g adalah serupa tertib pertama. Walaupun tiada nod penghubung tepi e dan nod g, ia mempunyai empat nod jiran yang sama, jadi nod e dan nod g adalah serupa tertib kedua.
daripada 🎜>. Seperti yang ditunjukkan dalam Rajah 1, kerana terdapat tepi yang menghubungkan nod f dan nod g, nod f dan nod g adalah serupa tertib pertama. Walaupun tiada nod penghubung tepi e dan nod g, ia mempunyai empat nod jiran yang sama, jadi nod e dan nod g adalah serupa tertib kedua. 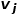
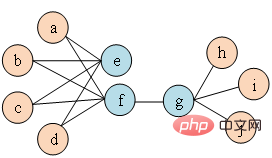
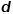 -vektor dimensi untuk mewakili graf, setiap vektor mewakili Pembenaman sebahagian daripada graf, seperti nod atau tepi.
-vektor dimensi untuk mewakili graf, setiap vektor mewakili Pembenaman sebahagian daripada graf, seperti nod atau tepi. 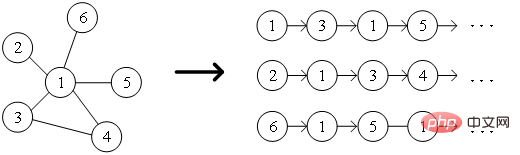
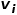 dalam graf, jujukan perkataan sepadan dengan jujukan nod yang diperolehi dengan jalan rawak, kemudian untuk jalan rawak
dalam graf, jujukan perkataan sepadan dengan jujukan nod yang diperolehi dengan jalan rawak, kemudian untuk jalan rawak 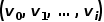 , tentukan fungsi objektif pengoptimumannya seperti yang ditunjukkan dalam formula.
, tentukan fungsi objektif pengoptimumannya seperti yang ditunjukkan dalam formula. 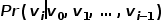
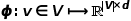 , untuk merealisasikan pemetaan nod dalam graf ke
, untuk merealisasikan pemetaan nod dalam graf ke 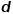 -vektor dimensi, maka masalah diubah menjadi anggaran kemungkinan formula berikut.
-vektor dimensi, maka masalah diubah menjadi anggaran kemungkinan formula berikut. 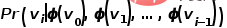
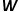 , dan satu lagi ialah matriks vektor perkataan latar belakang
, dan satu lagi ialah matriks vektor perkataan latar belakang  masing-masing mewakili vektor perkataan yang dikaitkan dengan perkataan apabila ia berfungsi sebagai peranan yang berbeza . Skip-gram ialah model untuk meramalkan konteks perkataan Ia mula-mula mempelajari hubungan antara perkataan daripada korpus, dan kemudian menggunakan hubungan ini untuk menyatakan konteks perkataan tertentu, iaitu perwakilan vektor perkataan. Maksudnya, dalam urutan yang sama, lebih kerap dua perkataan muncul pada masa yang sama, lebih serupa perwakilan vektor dua perkataan itu. Gunakan idea ini pada graf dan tentukan fungsi objektif pengoptimumannya seperti yang ditunjukkan dalam formula.
masing-masing mewakili vektor perkataan yang dikaitkan dengan perkataan apabila ia berfungsi sebagai peranan yang berbeza . Skip-gram ialah model untuk meramalkan konteks perkataan Ia mula-mula mempelajari hubungan antara perkataan daripada korpus, dan kemudian menggunakan hubungan ini untuk menyatakan konteks perkataan tertentu, iaitu perwakilan vektor perkataan. Maksudnya, dalam urutan yang sama, lebih kerap dua perkataan muncul pada masa yang sama, lebih serupa perwakilan vektor dua perkataan itu. Gunakan idea ini pada graf dan tentukan fungsi objektif pengoptimumannya seperti yang ditunjukkan dalam formula. 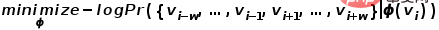
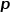 dan parameter
dan parameter 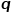 Bimbing sama ada setiap jalan rawak cenderung kepada pensampelan didahulukan keluasan atau pensampelan didahulukan dalam, jadi kebolehsuaian adalah tinggi. Dengan mengandaikan bahawa nod yang sedang dilawati
Bimbing sama ada setiap jalan rawak cenderung kepada pensampelan didahulukan keluasan atau pensampelan didahulukan dalam, jadi kebolehsuaian adalah tinggi. Dengan mengandaikan bahawa nod yang sedang dilawati 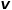 , kebarangkalian nod yang dilawati seterusnya
, kebarangkalian nod yang dilawati seterusnya 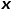 adalah seperti yang ditunjukkan dalam formula .
adalah seperti yang ditunjukkan dalam formula . 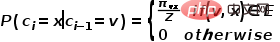
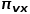 mewakili nod hamba
mewakili nod hamba 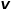 Kebarangkalian peralihan kepada nod
Kebarangkalian peralihan kepada nod 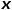 ,
, 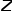 mewakili pemalar penormalan.
mewakili pemalar penormalan. 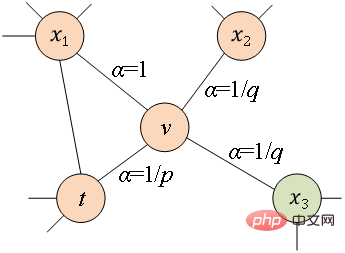
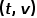 , dan langkah seterusnya ialah melawati nod x, biarkan
, dan langkah seterusnya ialah melawati nod x, biarkan 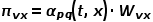 ,
, 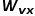 ialah berat tepi antara nod
ialah berat tepi antara nod 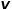 dan
dan 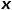 . Dalam erti kata lain, apabila graf ialah graf tidak berwajaran,
. Dalam erti kata lain, apabila graf ialah graf tidak berwajaran, 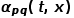 secara langsung menentukan kebarangkalian peralihan nod. Apabila graf ialah graf berwajaran, hasil darab
secara langsung menentukan kebarangkalian peralihan nod. Apabila graf ialah graf berwajaran, hasil darab 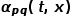 dan berat tepi
dan berat tepi 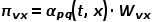 menentukan kebarangkalian peralihan akhir bagi nod itu.
menentukan kebarangkalian peralihan akhir bagi nod itu. 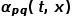 boleh dikira mengikut formula berikut, di mana
boleh dikira mengikut formula berikut, di mana 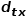 ialah nod
ialah nod 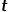 Jarak laluan terpendek antara dan nod
Jarak laluan terpendek antara dan nod 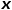 .
. 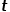 ke nod
ke nod 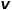 Apabila anda perlu memilih nod hop seterusnya, akan terdapat tiga situasi berikut.
Apabila anda perlu memilih nod hop seterusnya, akan terdapat tiga situasi berikut. 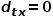 , kembalikan nod
, kembalikan nod 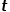 .
. 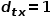 , pilih nod
, pilih nod 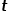 dan nod
dan nod 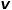 , contohnya, nod
, contohnya, nod 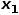 .
. 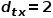 , pilih nod
, pilih nod 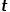 Nod bersebelahan dengan nod yang tidak berkaitan
Nod bersebelahan dengan nod yang tidak berkaitan 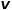 , seperti nod
, seperti nod 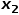 atau
atau 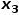 .
. 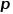 mengawal kebarangkalian untuk kembali ke nod hop sebelumnya, dan parameter
mengawal kebarangkalian untuk kembali ke nod hop sebelumnya, dan parameter 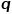 mengawal lebih banyak sama ada untuk meneroka maklumat struktur setempat atau maklumat struktur global bagi rangkaian sebenarnya
mengawal lebih banyak sama ada untuk meneroka maklumat struktur setempat atau maklumat struktur global bagi rangkaian sebenarnya 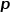 dan model Node2Vec apabila nilai
dan model Node2Vec apabila nilai 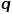 ditetapkan kepada 1.
ditetapkan kepada 1.
Atas ialah kandungan terperinci Perbincangan ringkas tentang algoritma pembenaman graf. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

