Rumah >Peranti teknologi >AI >Ahli sains komputer teori Boaz Barak: Pembelajaran mendalam bukanlah 'statistik mudah', dan jarak antara keduanya semakin jauh
Ahli sains komputer teori Boaz Barak: Pembelajaran mendalam bukanlah 'statistik mudah', dan jarak antara keduanya semakin jauh
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-12 17:34:161353semak imbas
Pada 1990-an, Rob Tibshirani, seorang profesor bioinformatik terkenal di Universiti Stanford, merangka perbendaharaan kata untuk membuat surat-menyurat yang mudah dan kasar antara konsep yang berbeza dalam pembelajaran mesin dan statistik:

Di satu pihak, jadual ini memberikan pemahaman asas tentang pembelajaran mesin, tetapi pada masa yang sama, ia hanya meringkaskan konsep dalam pembelajaran mendalam atau pembelajaran mesin Ia adalah maksud perkataan dalam statistik, dan ia juga menyebabkan kecenderungan kognitif kebanyakan orang terhadap sifat pembelajaran mendalam: iaitu, pembelajaran mendalam ialah "statistik mudah".
Walau bagaimanapun, dalam perbincangan yang mendalam, kognisi ini telah menghalang penyelidik sedikit sebanyak daripada memahami sebab-sebab penting untuk kejayaan pembelajaran mendalam. Dalam artikel "Hubungan yang tidak selesa antara pembelajaran mendalam dan statistik (klasik)" pada bulan Jun tahun ini, Boaz Barak, seorang profesor Harvard yang terkenal dan saintis komputer teori, membandingkan dan membezakan pembelajaran dan statistik mendalam, menunjukkan asas pembelajaran mendalam . Faktor konstituen adalah sangat berbeza daripada statistik.
Boaz Barak membuat pemerhatian penting: Dari perspektif tujuan model, jika ia memfokuskan kepada ramalan dan pemerhatian, maka model pembelajaran mendalam dengan ciri kotak hitam mungkin yang terbaik. pilihan; tetapi Jika anda ingin mendapatkan pemahaman sebab-sebab sesuatu dan meningkatkan kebolehtafsiran, maka model "mudah" mungkin berprestasi lebih baik. Ini bertepatan dengan pandangan "kesederhanaan" yang dicadangkan oleh tiga saintis Ma Yi, Cao Ying, dan Shen Xiangyang bulan lepas, yang merupakan salah satu daripada dua prinsip utama kecerdasan.
Pada masa yang sama, Boaz Barak membincangkan keserasiannya dengan pembelajaran mendalam dengan menunjukkan dua kes senario yang berbeza untuk menyesuaikan model statistik dan pembelajaran matematik, manakala matematik dan kod kerana pembelajaran mendalam adalah hampir sama dengan model statistik yang sesuai, pada tahap yang lebih mendalam sebahagian besar pembelajaran mendalam boleh ditangkap dalam senario "kemahiran mengajar kepada pelajar".
Tidak dinafikan bahawa pembelajaran statistik memainkan peranan penting dalam pembelajaran mendalam. Tetapi apa yang pasti ialah perspektif statistik tidak dapat memberikan gambaran yang lengkap untuk memahami pembelajaran mendalam Untuk memahami aspek pembelajaran mendalam yang berbeza, orang masih perlu mendekatinya dari perspektif yang berbeza.
Berikut ialah perbincangan Boaz Barak:
1 Ramalan dan penjelasan dalam pemasangan model
Selama beribu-ribu tahun, saintis telah menyesuaikan model dengan pemerhatian. Sebagai contoh, seperti yang disebutkan dalam kulit buku falsafah sains, ahli astronomi Mesir Ptolemy mencadangkan model gerakan planet yang bijak. Model Ptolemy adalah geosentrik (iaitu, planet berputar mengelilingi Bumi), tetapi mempunyai satu siri "tombol" (khususnya, epicycles) yang memberikan ketepatan ramalan yang sangat baik. Sebaliknya, model heliosentrik asal Copernicus mengandaikan orbit bulat planet mengelilingi matahari. Ia lebih ringkas (kurang "tombol boleh tala") dan lebih betul secara keseluruhan daripada model Ptolemy, tetapi kurang tepat dalam meramalkan pemerhatian. (Copernicus juga kemudiannya menambah epicycles sendiri, sekali gus menyaingi prestasi Ptolemy.)
Ptolemy's dan Copernicus's Model ini tiada tandingannya. Apabila anda memerlukan "kotak hitam" untuk membuat ramalan, model geosentrik Ptolemaic adalah unggul. Dan jika anda mahukan model mudah yang boleh "mengintip ke dalam" dan berfungsi sebagai titik permulaan teori untuk menerangkan gerakan bintang, maka model Copernicus adalah lebih baik.
Malah, Kepler akhirnya memperhalusi model Copernicus ke dalam orbit elips dan mencadangkan tiga undang-undang pergerakan planetnya, yang membenarkan Newton menggunakan yang sama yang digunakan di Bumi Undang-undang graviti menjelaskannya . Untuk tujuan ini, adalah penting bahawa model heliosentrik bukan hanya "kotak hitam" yang menyediakan ramalan, tetapi sebaliknya diberikan oleh persamaan matematik mudah dengan beberapa "bahagian bergerak". Astronomi telah menjadi sumber inspirasi untuk membangunkan teknik statistik selama bertahun-tahun. Gauss dan Legendre (secara bebas) mencipta regresi kuasa dua terkecil sekitar tahun 1800 untuk meramal orbit asteroid dan benda angkasa lain ciptaan Cauchy tentang keturunan kecerunan pada tahun 1847 juga didorong oleh ramalan astronomi.
Dalam fizik, (sekurang-kurangnya kadangkala) anda boleh "mempunyai semuanya" - cari teori "betul" yang memberi anda ketepatan ramalan terbaik dan penjelasan terbaik data anda, seperti yang dijelaskan oleh prinsip seperti Occam's Pencukur Pandangan sedemikian menangkap andaian bahawa kesederhanaan, kuasa ramalan, dan wawasan penjelasan semuanya konsisten. Walau bagaimanapun, dalam banyak bidang lain, terdapat ketegangan antara matlamat berkembar penjelasan (atau, lebih umum, wawasan) dan ramalan. Jika anda hanya ingin meramalkan pemerhatian, "kotak hitam" mungkin pilihan terbaik. Tetapi jika anda mengekstrak model kausal, prinsip umum atau ciri penting, maka model ringkas yang mudah difahami dan dijelaskan mungkin lebih baik.
Pilihan model yang betul bergantung pada tujuannya. Sebagai contoh, pertimbangkan set data yang mengandungi ekspresi gen dan fenotip bagi banyak individu (katakan, untuk penyakit tertentu jika matlamatnya adalah untuk meramalkan peluang seseorang jatuh sakit, seseorang itu selalunya ingin menggunakan model terbaik untuk tugas itu). , tidak kira betapa kompleks atau Berapa banyak gen ia bergantung kepada. Sebaliknya, jika matlamat anda adalah untuk mengenal pasti beberapa gen untuk kajian lanjut dalam makmal basah, kotak hitam yang canggih akan digunakan secara terhad, walaupun ia sangat tepat.
Pada tahun 2001, Leo Breiman menerangkan perkara ini dengan berkesan dalam artikel terkenalnya "Pemodelan Statistik: Dua Budaya" mengenai pemodelan statistik. "Budaya pemodelan data" memfokuskan pada model generatif mudah yang menerangkan data, manakala "budaya pemodelan algoritma" tidak memahami cara data dijana, tetapi menumpukan pada mencari model yang boleh meramal data. Breiman percaya bahawa statistik terlalu dikuasai oleh budaya pertama dan fokus ini "membawa kepada teori yang tidak relevan dan kesimpulan saintifik yang boleh dipersoalkan" dan "menghalang ahli statistik daripada mengkaji soalan baharu yang menarik."
Walau bagaimanapun, kertas Breiman adalah kontroversi. Walaupun Brad Efron bersetuju dengan beberapa sentimen, “Pada pandangan pertama, makalah menarik Leo Breiman nampaknya menolak kesederhanaan dan pandangan saintifik yang memihak kepada kotak hitam dengan banyak tombol untuk dimanipulasi sama.” Tetapi dalam artikel baru-baru ini ("Ramalan, Anggaran dan Atribusi"), Efron dengan murah hati mengakui bahawa "ternyata Breiman lebih tepat daripada saya: Algoritma ramalan tulen telah menjadi tumpuan statistik pada abad ke-21, dan perkembangan mereka Hala tujunya hampir sama dengan apa yang Leo sebutkan sebelum ini , semuanya milik apa yang Breiman panggil sebagai budaya kedua, iaitu, tertumpu pada ramalan, yang telah beredar sejak sekian lama. Sebagai contoh, buku teks Duda dan Hart 1973 "Menyahbina Pengagihan: Rangka Kerja Bertujuan Pembelajaran" dan kertas kerja Highleyman 1962 "Reka Bentuk dan Analisis Eksperimen Pengecaman Corak" amat dikenali oleh pengamal pembelajaran mendalam masa kini:
Begitu juga, set data aksara tulisan tangan Highleyman dan seni bina Chow yang digunakan untuk memuatkan set data (ketepatan adalah lebih kurang 58%) juga bergema dengan pembaca moden.

Mengapakah pembelajaran mendalam berbeza?
Pada tahun 1992, Stuart Geman, Elie Bienenstock dan Rene Doursat bersama-sama menulis makalah bertajuk "Rangkaian Neural dan Dilema Bias/Varian" yang mengambil beberapa pandangan pesimis, cth tidak mencukupi untuk menyelesaikan masalah sukar dalam persepsi mesin dan pembelajaran mesin"; khususnya, mereka percaya bahawa rangkaian saraf tujuan umum tidak dapat menyelesaikan tugas yang sukar dengan jayanya, dan satu-satunya cara untuk rangkaian saraf berjaya adalah melalui ciri rekaan Tangan. Dalam kata-kata mereka: "Ciri-ciri penting mesti terbina dalam atau 'berwayar keras'... dan bukannya dipelajari melalui kaedah statistik.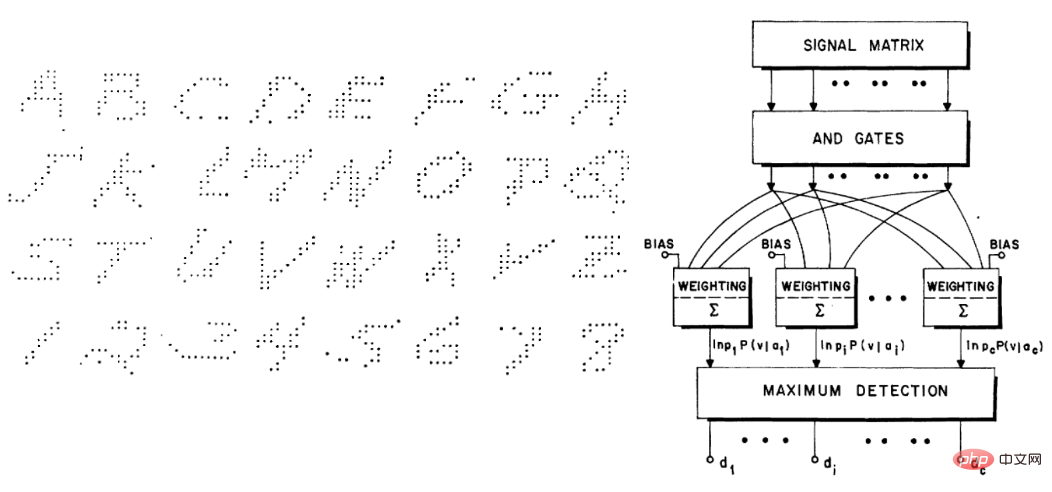
” Jika difikirkan semula, mereka silap. Selain itu, seni bina rangkaian saraf moden seperti Transformer adalah lebih serba boleh daripada rangkaian konvolusi pada masa itu. Tetapi menarik untuk memahami sebab di sebalik kesilapan mereka.
Saya rasa sebab mereka melakukan kesilapan ialah pembelajaran mendalam sememangnya berbeza daripada kaedah pembelajaran lain. Fenomena a priori ialah pembelajaran mendalam nampaknya hanya mempunyai satu lagi model ramalan, seperti jiran terdekat atau hutan rawak. Ia mungkin mempunyai lebih banyak "tombol" tetapi itu nampaknya merupakan perbezaan kuantitatif dan bukannya kualitatif. Dalam kata-kata PW Andreson, "lebih banyak adalah berbeza".
Dalam fizik, apabila skala berubah dengan beberapa urutan magnitud, kita selalunya hanya memerlukan teori yang berbeza sama sekali untuk menerangkannya, dan perkara yang sama berlaku untuk pembelajaran mendalam. Malah, pembelajaran mendalam beroperasi sepenuhnya berbeza daripada model klasik (parametrik atau bukan parametrik), walaupun dari peringkat tinggi persamaan (dan kod Python) kelihatan sama.
Untuk menjelaskan perkara ini, mari kita lihat proses pembelajaran dua contoh yang sangat berbeza: Memasang model statistik dan mengajar pelajar mempelajari matematik.
Senario A: Memasang model statistik
Secara umumnya, langkah-langkah untuk memasang model statistik kepada data adalah seperti berikut:
1. Mari kita perhatikan beberapa data x dan y. x boleh dianggap sebagai matriks n 🎜>, dengan 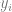 ialah hingar yang sepadan, hingar aditif digunakan untuk kesederhanaan dan
ialah hingar yang sepadan, hingar aditif digunakan untuk kesederhanaan dan 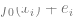 ialah label kebenaran asas yang betul . )
ialah label kebenaran asas yang betul . )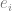 2 Dengan menjalankan beberapa algoritma pengoptimuman, kita boleh menyesuaikan model
2 Dengan menjalankan beberapa algoritma pengoptimuman, kita boleh menyesuaikan model 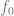 kepada data supaya
kepada data supaya
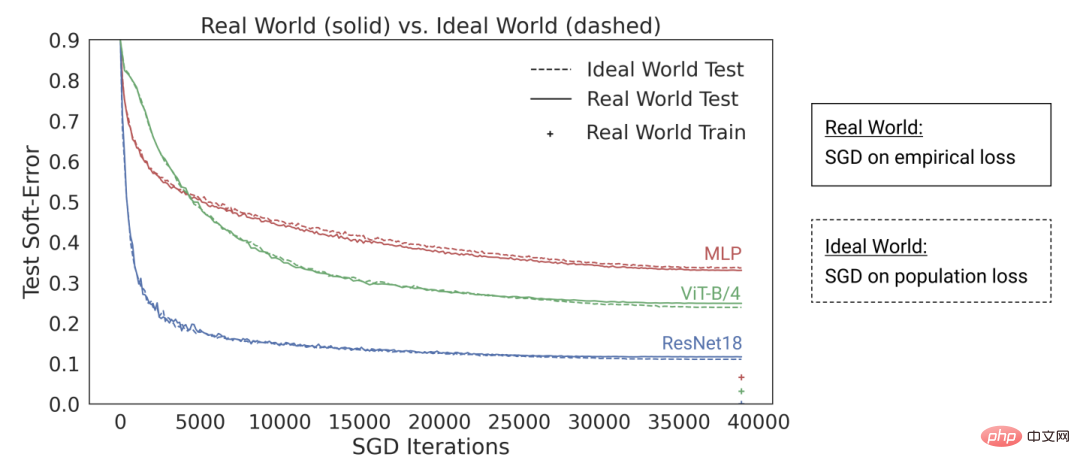
The risiko pengalaman adalah minimum. Iaitu, kami menggunakan algoritma pengoptimuman untuk mencari bilangan terminimum 3 Kami berharap model kami boleh mengalami kerugian keseluruhan yang baik kerana ralat/kerugian generalisasi Ilustrasi: Kartun Bradley Efron tentang Hukum Pertama Newton diterbitkan semula melalui pemerhatian bunyi Paradigma yang sangat umum ini merangkumi banyak tetapan, termasuk regresi linear kuasa dua terkecil, jiran terdekat, latihan rangkaian saraf dan banyak lagi. Dalam tetapan statistik klasik, kami menjangkakan untuk melihat perkara berikut: Pertukaran bias/varian: Biarkan F sebagai set model yang dioptimumkan. (Apabila kita berada dalam tetapan tidak cembung dan/atau mempunyai istilah regularizer, kita boleh membiarkan F menjadi set model sedemikian yang boleh dilaksanakan oleh algoritma dengan kebarangkalian tidak boleh diabaikan, memandangkan kesan pilihan algoritma dan regularizer. ) Sisihan F ialah anggaran terbaik kepada label yang betul dan boleh dicapai oleh elemen Oleh itu, pembelajaran statistik selalunya menunjukkan pertukaran bias/varian dan meminimumkan ralat keseluruhan melalui "pilihan Goldilocks" kerumitan model yang betul. Malah, Geman et al melakukan perkara itu, mewajarkan pesimisme mereka tentang rangkaian saraf dengan mengatakan bahawa "batasan asas yang terhasil daripada dilema bias-varian digunakan untuk semua model inferens bukan parametrik, termasuk rangkaian saraf." Lebih banyak bukan selalunya yang terbaik. Dalam pembelajaran statistik, mendapatkan lebih banyak ciri atau data tidak semestinya meningkatkan prestasi. Sebagai contoh, belajar daripada data yang mengandungi banyak ciri yang tidak berkaitan adalah lebih mencabar. Begitu juga, belajar daripada model campuran, di mana data datang daripada satu daripada dua taburan (cth. Pulangan yang semakin berkurangan. Dalam banyak kes, bilangan titik data yang diperlukan untuk mengurangkan hingar ramalan kepada beberapa parameter Pergantungan yang kuat pada kehilangan, data. Apabila menyesuaikan model pada data berdimensi tinggi, butiran kecil mungkin membuat perbezaan besar dalam hasil. Ahli statistik tahu bahawa pilihan seperti L1 atau L2 regularizer adalah penting, apatah lagi menggunakan set data yang berbeza sama sekali, bilangan pengoptimum dimensi tinggi yang berbeza akan menjadi sangat berbeza. Titik data tidak mempunyai "kesukaran" semula jadi (sekurang-kurangnya dalam beberapa kes). Secara tradisinya, titik data diambil secara berasingan daripada pengedaran. Walaupun titik yang hampir dengan sempadan keputusan mungkin lebih sukar untuk dikelaskan, memandangkan kepekatan ukuran dimensi tinggi, adalah dijangka bahawa kebanyakan titik akan mempunyai jarak yang sama. Oleh itu, sekurang-kurangnya dalam pengagihan data klasik, mata tidak dijangka berbeza jauh dalam tahap kesukarannya. Walau bagaimanapun, model campuran boleh menunjukkan tahap kesukaran yang berbeza bagi perbezaan ini, jadi tidak seperti masalah lain yang dinyatakan di atas, perbezaan ini tidaklah begitu mengejutkan dalam tetapan statistik. Berbeza dengan perkara di atas, mari kita bercakap tentang mengajar pelajar beberapa topik matematik tertentu (seperti mengira terbitan) dan memberi mereka bimbingan umum dan keperluan Lakukan latihan. Ini bukan tetapan yang ditakrifkan secara rasmi, tetapi beberapa ciri kualitatifnya boleh dipertimbangkan: Kapsyen: Pelajari matematik khusus daripada IXL laman web Amalan Kemahiran Pelajari kemahiran, bukan pengagihan anggaran. Dalam kes ini, pelajar sedang mempelajari kemahiran dan bukannya beberapa penganggar/peramal. Walaupun mentakrifkan "kemahiran" bukanlah tugas yang remeh, ia adalah matlamat yang berbeza secara kualitatif. Khususnya, walaupun latihan pemetaan fungsi tidak boleh digunakan sebagai "kotak hitam" untuk menyelesaikan beberapa tugasan X yang berkaitan, kami percaya bahawa perwakilan dalaman yang pelajar bentuk semasa menyelesaikan masalah ini masih berguna untuk X. Lebih banyak, lebih baik. Secara umumnya, pelajar akan mencapai keputusan yang lebih baik jika mereka mempraktikkan lebih banyak soalan dan jenis soalan yang berbeza. Tetapi sebenarnya, "model hibrid"—melakukan beberapa masalah kalkulus dan beberapa masalah algebra—tidak menjejaskan prestasi pelajar dalam kalkulus dan sebenarnya membantu mereka belajar. "Teroka" atau buka kunci ciri, beralih kepada perwakilan automatik. Walaupun terdapat pulangan yang semakin berkurangan untuk menyelesaikan masalah pada satu ketika, pelajar nampaknya melalui peringkat di mana melakukan masalah membantu konsep "klik" dan membuka kunci ciri baharu. Selain itu, apabila pelajar mengulangi jenis masalah tertentu, mereka nampaknya mengalihkan keupayaan dan perwakilan masalah tersebut ke tahap yang lebih rendah, membolehkan mereka mengembangkan beberapa automatik dengan masalah yang tidak mereka hadapi sebelum ini. Prestasi sebahagiannya bebas daripada kehilangan dan data. Terdapat lebih daripada satu cara untuk mengajar konsep matematik, dan walaupun pelajar belajar menggunakan buku, kaedah pendidikan atau sistem penggredan yang berbeza, mereka masih akan mempelajari bahan yang sama dan perwakilan dalaman yang serupa. Sesetengah soalan lebih sukar. Dalam latihan matematik, kita sering dapat melihat perkaitan yang kuat dalam kaedah yang digunakan oleh pelajar yang berbeza untuk menyelesaikan masalah yang sama. Kesukaran masalah nampaknya telah diperbaiki, dan susunan penyelesaian teka-teki juga ditetapkan, yang membolehkan proses pembelajaran dioptimumkan. Inilah sebenarnya yang dilakukan oleh platform seperti IXL. Jadi, yang manakah antara dua metafora di atas lebih menggambarkan pembelajaran mendalam moden, dan khususnya mengapa ia begitu berjaya? Pemasangan model statistik kelihatan lebih konsisten dengan matematik dan kod. Malah, gelung latihan Pytorch kanonik melatih rangkaian yang mendalam melalui pengurangan risiko empirikal seperti yang diterangkan di atas: Walau bagaimanapun, secara lebih mendalam Secara Hierarki, hubungan antara dua tetapan tidak begitu jelas. Secara khusus, ia boleh dijalankan dengan membaiki tugas pembelajaran tertentu dan menggunakan kaedah "pembelajaran kendiri + kuar linear (linear probe)" untuk melatih algoritma klasifikasi adalah seperti berikut: 1. Anggapkan bahawa data ialah jujukan 2. Mula-mula cari rangkaian saraf dalam untuk mewakili fungsi 3 Kemudian kami menggunakan data berlabel lengkap Mempelajari kemahiran dan bukannya menghampiri fungsi. Pembelajaran penyeliaan kendiri bukan tentang menghampiri fungsi, tetapi perwakilan pembelajaran yang boleh digunakan untuk pelbagai tugas hiliran. Dengan mengandaikan bahawa ini adalah paradigma yang dominan dalam pemprosesan bahasa semula jadi, sama ada tugasan hiliran diperoleh melalui probing linear, penalaan halus atau gesaan adalah kedua. Lebih banyak, lebih baik. Dalam pembelajaran penyeliaan kendiri, kualiti perwakilan bertambah baik apabila jumlah data meningkat. Dan, lebih pelbagai data, lebih baik. Kapsyen: Set Data model Google PaLM Buka kunci kebolehan. Peningkatan tidak berterusan dalam model pembelajaran mendalam dilihat dari semasa ke semasa apabila sumber (data, pengiraan, saiz model) berkembang, dan ini juga ditunjukkan dalam beberapa persekitaran sintetik. Nota gambar: Apabila saiz model meningkat, model PaLM menunjukkan beberapa penambahbaikan diskret dalam beberapa penanda aras (hanya terdapat tiga kaveat saiz dalam rajah di atas) dan membuka kunci beberapa perintah Fungsi yang mengejutkan orang ramai, seperti menerangkan jenaka. Prestasi sebahagian besarnya bebas daripada kehilangan atau data. Lebih daripada satu kehilangan yang diawasi sendiri, beberapa kehilangan kontras dan rekonstruktif digunakan untuk imej. Model bahasa kadangkala menggunakan pembinaan semula sebelah pihak (meramalkan token seterusnya), dan kadangkala menggunakan model penyamaran, di mana matlamatnya adalah untuk meramal input bertopeng daripada token kiri dan kanan. Ia juga mungkin menggunakan set data yang sedikit berbeza, yang mungkin menjejaskan kecekapan, tetapi selagi pilihan "munasabah" dibuat, secara amnya sumber asal adalah lebih baik daripada yang khusus digunakan Kehilangan atau set data lebih meramalkan prestasi. Sesetengah keadaan lebih sukar daripada yang lain. Ini tidak terhad kepada pembelajaran diselia sendiri, titik data mungkin mempunyai beberapa "tahap kesukaran" yang wujud. Malah, terdapat beberapa bukti praktikal bahawa algoritma pembelajaran yang berbeza mempunyai "tahap kemahiran" yang berbeza dan mata yang berbeza mempunyai "tahap kesukaran" yang berbeza (Kebarangkalian bahawa pengelas f dengan betul mengelaskan x meningkat sehala dengan kemahiran f dan menurun sehala dengan kesukaran x). Paradigma "kemahiran dan kesukaran" adalah penjelasan paling jelas tentang fenomena "ketepatan dalam talian" yang ditemui oleh Recht dan Miller et al., dan dalam kertas yang saya tulis bersama Kaplun, Ghosh, Garg, dan Nakkiran, saya juga menunjukkan bahawa dalam set data Bagaimana input yang berbeza mempunyai "tandatangan kesukaran" yang sedia ada yang secara konvensional kelihatan teguh kepada model yang berbeza. Carta: Graf Miller et al. menunjukkan pengelas yang dilatih pada CIFAR-10 dan diuji pada CINIC-10 Fenomena garis ketepatan Pengagihan: Rangka Kerja Pembelajaran Bertitik tolak" untuk mendapatkan bilangan pengelas sumber yang semakin meningkat. Carta teratas menggambarkan kebarangkalian softmax yang berbeza untuk kelas yang berkemungkinan besar sebagai fungsi ketepatan global pengelas yang diindeks mengikut masa latihan; carta pai bawah menunjukkan pecahan set data yang berbeza kepada jenis mata yang berbeza. Terutama, penguraian ini serupa untuk seni bina saraf yang berbeza. Latihan moden model besar kelihatan lebih seperti mengajar pelajar daripada menyesuaikan model kepada data, mengambil "rehat" atau mencuba perkara lain apabila pelajar tidak faham atau kelihatan letih (penyimpangan latihan) Cara . Log latihan untuk model besar Meta adalah instruktif - sebagai tambahan kepada isu perkakasan, seseorang juga boleh melihat beberapa campur tangan seperti menukar algoritma pengoptimuman yang berbeza semasa latihan, dan juga mempertimbangkan fungsi pengaktifan "hot-swapping" (GELU kepada RELU). Yang terakhir tidak masuk akal jika anda menganggap latihan model sebagai data yang sesuai daripada mempelajari perwakilan. Ilustrasi: Petikan daripada log latihan Meta Dua situasi dibincangkan di bawah: Sejauh ini, kita hanya membincangkan pembelajaran yang diselia sendiri, tetapi contoh pembelajaran mendalam masih diawasi. pembelajaran ialah "ImageNet Moments" adalah daripada ImageNet. Jadi, adakah perkara yang kita bincangkan di atas terpakai kepada pembelajaran diselia? Pertama, Kemunculan pembelajaran mendalam berskala besar yang diselia sedikit sebanyak merupakan satu kemalangan sejarah, berkat ketersediaan set data berlabel yang besar dan berkualiti tinggi (iaitu, ImageNet). Adalah mungkin untuk membayangkan sejarah alternatif: pembelajaran mendalam mula-mula membuat penemuan dalam pemprosesan bahasa semula jadi melalui pembelajaran tanpa pengawasan, dan kemudian beralih kepada pembelajaran visi dan diselia. Kedua, terdapat beberapa bukti bahawa pembelajaran penyeliaan dan pembelajaran penyeliaan kendiri berkelakuan serupa "di belakang tabir" walaupun mereka menggunakan fungsi kehilangan yang sama sekali berbeza. Kedua-duanya biasanya mencapai prestasi yang sama. Ia juga ditemui dalam kertas kerja "Meninjau Semula Jahitan Model untuk Membandingkan Perwakilan Neural" bahawa mereka mempelajari perwakilan dalaman yang serupa. Khususnya, untuk setiap Kapsyen: Jadual daripada kertas kerja pasukan Hinton "Model Penyeliaan Kendiri Besar ialah Pelajar Separa Selia yang Kuat". Perhatikan persamaan umum dalam prestasi antara pembelajaran diselia, penalaan halus (100%) penyeliaan sendiri dan pengesanan linear penyeliaan sendiri Ilustrasi: Model yang diselia dan diselia sendiri yang dipetik daripada kertas kerja "Meninjau Semula Jahitan Model untuk Membandingkan Perwakilan Neural". Kiri - Jika model yang diselia sendiri adalah 3% kurang tepat daripada model yang diselia, maka perwakilan yang serasi sepenuhnya akan dikenakan penalti penyambungan sebanyak p 3% (apabila lapisan p adalah daripada model yang diselia sendiri). Jika model tidak serasi sepenuhnya, jangkakan ketepatan menurun secara mendadak apabila lebih banyak model dicantum bersama. Kanan - Keputusan sebenar penyambungan model yang diselia sendiri yang berbeza. Kelebihan model penyeliaan sendiri + ringkas ialah ia boleh memuatkan pembelajaran ciri atau "magis pembelajaran mendalam" (hasil daripada fungsi perwakilan mendalam) dengan model statistik (Dilakukan oleh pengelas "mudah" linear atau lain, dipisahkan di atas perwakilan ini) . Akhirnya, walaupun spekulatif, nampaknya "pembelajaran meta" sering disamakan dengan fakta bahawa perwakilan pembelajaran (lihat karya "Pembelajaran Cepat atau Penggunaan Semula Ciri? Ke Arah Pemahaman Keberkesanan" untuk butiran MAML"), boleh dilihat sebagai satu lagi bukti yang menyokong maksud artikel ini, tanpa mengira model yang kononnya dioptimumkan. Pembaca mungkin perasan bahawa saya melangkau contoh tipikal perbezaan antara model pembelajaran statistik dan model pembelajaran mendalam dalam aplikasi praktikal, iaitu , kekurangan "pertukaran bias-varian" dan keupayaan generalisasi yang sangat baik bagi model terparameter berlebihan. Ada dua sebab mengapa saya tidak akan bercakap tentang contoh ini secara terperinci: Pertama, jika pembelajaran yang diselia memang sama dengan diri sendiri -penyeliaan + "lapisan bawah" mudah "Pembelajaran, kemudian keupayaan generalisasinya boleh dijelaskan (untuk butiran, sila lihat kertas "Untuk pembelajaran penyeliaan sendiri, Rasionaliti membayangkan generalisasi, terbukti"); Kedua, saya rasaPenparameteran berlebihan bukanlah kunci kejayaan dalam pembelajaran mendalam. Apa yang menjadikan rangkaian dalam istimewa bukan kerana ia besar berbanding bilangan sampel, tetapi ia besar secara mutlak. Malah, selalunya tiada penparameteran berlebihan dalam model pembelajaran tanpa seliaan/seliaan sendiri. Walaupun untuk model bahasa berskala besar, mereka hanya mempunyai set data yang lebih besar, tetapi itu tidak menjadikan prestasi mereka kurang misteri. Nota gambar: Dalam kertas kerja "The Deep Bootstrap Framework: Good Online Learners are Good Offline Generalizers", penemuan penyelidik menunjukkan bahawa seni bina pembelajaran mendalam hari ini mengalami "over-parameterization" dan The performance adalah serupa dalam keadaan "undersampled" (di mana model dilatih pada data terhad untuk banyak generasi sehingga ia melebihi: "dunia nyata" yang ditunjukkan di atas), dalam kes "underparameterized" dan "dalam talian" Ini juga benar (di mana model hanya dilatih untuk satu generasi, dan setiap sampel hanya dilihat sekali: iaitu, "dunia ideal" dalam gambar di atas) Tidak dinafikan bahawa pembelajaran statistik memainkan peranan penting dalam pembelajaran mendalam. Walau bagaimanapun, jika anda menganggap pembelajaran mendalam hanya sebagai model yang lebih sesuai daripada model klasik, anda terlepas banyak faktor di sebalik kejayaannya. Metafora yang dipanggil "pelajar manusia" adalah lebih tidak sesuai. Pembelajaran mendalam adalah serupa dengan evolusi biologi kerana walaupun terdapat banyak aplikasi berulang bagi peraturan yang sama (iaitu keturunan kecerunan dengan kehilangan pengalaman), ia menghasilkan hasil yang sangat kompleks. Komponen rangkaian saraf yang berbeza nampaknya mempelajari perkara yang berbeza pada masa yang berbeza, termasuk pembelajaran perwakilan, pemasangan ramalan, penyusunan tersirat dan hingar tulen. Kami masih mencari lensa yang sesuai untuk bertanya tentang pembelajaran mendalam, apatah lagi menjawabnya. Perjalanan masih panjang, dan kami akan bekerjasama untuk menggalakkan anda. 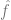
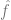 , dengan
, dengan 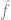 ialah istilah kerugian (menangkap
ialah istilah kerugian (menangkap 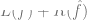
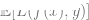 adalah kecil (ramalan ini adalah berdasarkan data keseluruhan di mana data eksperimen adalah untuk memperoleh).
adalah kecil (ramalan ini adalah berdasarkan data keseluruhan di mana data eksperimen adalah untuk memperoleh). 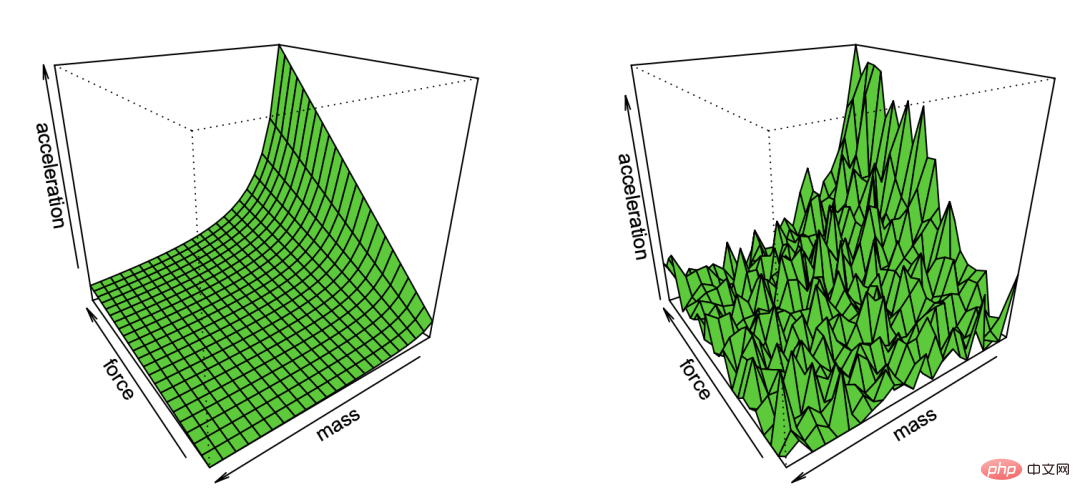
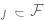 . Lebih besar kelas F, lebih kecil sisihan Apabila
. Lebih besar kelas F, lebih kecil sisihan Apabila 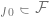 , sisihan malah boleh menjadi sifar. Walau bagaimanapun, apabila kelas F lebih besar, lebih banyak sampel diperlukan untuk mengecilkan julat keahliannya, dan dengan itu varians dalam model output algoritma adalah lebih besar. Ralat generalisasi keseluruhan ialah jumlah bagi istilah bias dan sumbangan varians.
, sisihan malah boleh menjadi sifar. Walau bagaimanapun, apabila kelas F lebih besar, lebih banyak sampel diperlukan untuk mengecilkan julat keahliannya, dan dengan itu varians dalam model output algoritma adalah lebih besar. Ralat generalisasi keseluruhan ialah jumlah bagi istilah bias dan sumbangan varians.  dan
dan  ), adalah lebih sukar daripada mempelajari individu secara bebas.
), adalah lebih sukar daripada mempelajari individu secara bebas.  adalah dalam urutan
adalah dalam urutan  di bawah beberapa parameter k Pengembangan borang. Dalam kes ini, ia mengambil masa kira-kira k sampel untuk "berlepas", dan sebaik sahaja anda melakukan ini, anda akan menghadapi sistem pulangan yang semakin berkurangan, iaitu, dengan mengandaikan bahawa ia mengambil n mata untuk mencapai (katakan) ketepatan 90%, maka anda mahu Untuk meningkatkan ketepatan kepada 95%, lebih kurang 3n mata lagi diperlukan. Secara umumnya, apabila sumber bertambah (sama ada data, kerumitan model atau pengiraan), kami berharap dapat menangkap perbezaan yang lebih terperinci daripada membuka kunci keupayaan kualitatif baharu.
di bawah beberapa parameter k Pengembangan borang. Dalam kes ini, ia mengambil masa kira-kira k sampel untuk "berlepas", dan sebaik sahaja anda melakukan ini, anda akan menghadapi sistem pulangan yang semakin berkurangan, iaitu, dengan mengandaikan bahawa ia mengambil n mata untuk mencapai (katakan) ketepatan 90%, maka anda mahu Untuk meningkatkan ketepatan kepada 95%, lebih kurang 3n mata lagi diperlukan. Secara umumnya, apabila sumber bertambah (sama ada data, kerumitan model atau pengiraan), kami berharap dapat menangkap perbezaan yang lebih terperinci daripada membuka kunci keupayaan kualitatif baharu. Senario B: Pembelajaran Matematik
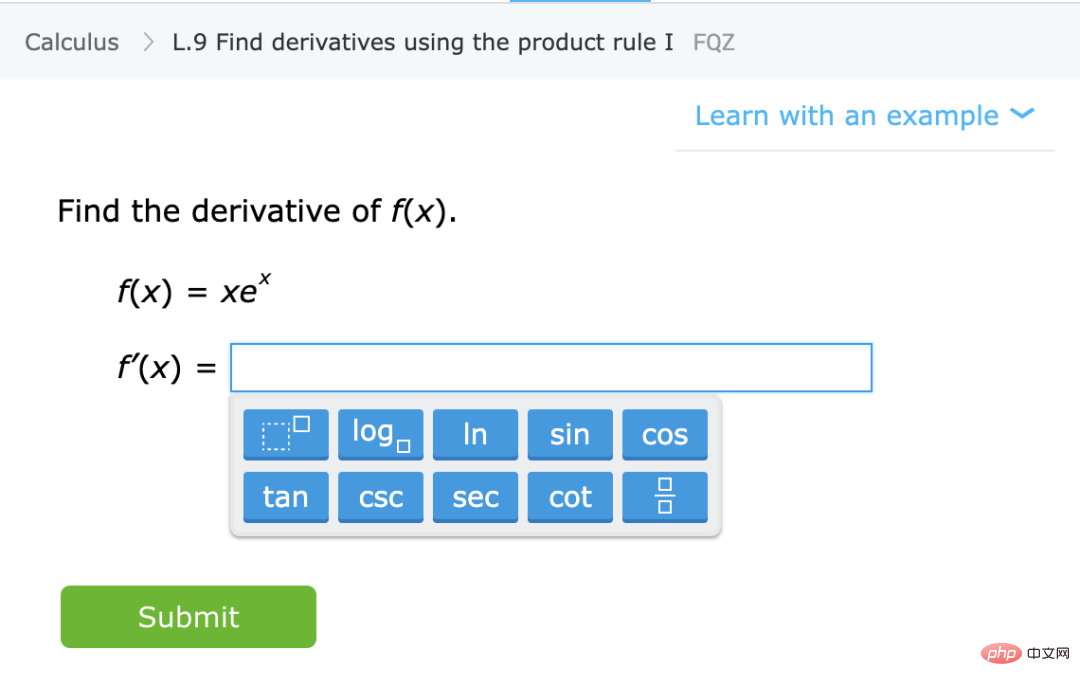
4 Adakah pembelajaran mendalam lebih seperti anggaran statistik atau teknik pembelajaran pelajar?

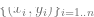 , dengan
, dengan 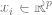 ialah titik data tertentu (seperti imej tertentu),
ialah titik data tertentu (seperti imej tertentu), 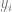 ialah tag.
ialah tag. 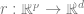 Latihan fungsi ini hanya menggunakan titik data
Latihan fungsi ini hanya menggunakan titik data 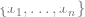 Daripada menggunakan label, dengan meminimumkan beberapa jenis fungsi kehilangan yang diawasi sendiri. Contoh fungsi kehilangan tersebut ialah pembinaan semula atau gambar dalam gambar (memulihkan sebahagian daripada input x lain) atau pembelajaran kontrastif (mencari
Daripada menggunakan label, dengan meminimumkan beberapa jenis fungsi kehilangan yang diawasi sendiri. Contoh fungsi kehilangan tersebut ialah pembinaan semula atau gambar dalam gambar (memulihkan sebahagian daripada input x lain) atau pembelajaran kontrastif (mencari 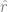 supaya
supaya 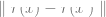 adalah ketara Lebih kecil , apabila
adalah ketara Lebih kecil , apabila 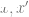 ialah kenaikan titik data yang sama, hubungan selari adalah jauh lebih kecil daripada hubungan selari antara dua titik rawak).
ialah kenaikan titik data yang sama, hubungan selari adalah jauh lebih kecil daripada hubungan selari antara dua titik rawak). 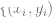 untuk memuatkan pengelas linear
untuk memuatkan pengelas linear 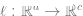 (di mana C ialah kelas. nombor) untuk meminimumkan kehilangan entropi silang. Pengelas akhir menghasilkan pemetaan
(di mana C ialah kelas. nombor) untuk meminimumkan kehilangan entropi silang. Pengelas akhir menghasilkan pemetaan 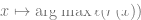 . Langkah 3 hanya sesuai untuk pengelas linear, jadi "keajaiban" berlaku dalam langkah 2 (pembelajaran rangkaian dalam yang diselia sendiri). Dalam pembelajaran penyeliaan kendiri, beberapa sifat yang boleh dilihat termasuk:
. Langkah 3 hanya sesuai untuk pengelas linear, jadi "keajaiban" berlaku dalam langkah 2 (pembelajaran rangkaian dalam yang diselia sendiri). Dalam pembelajaran penyeliaan kendiri, beberapa sifat yang boleh dilihat termasuk: 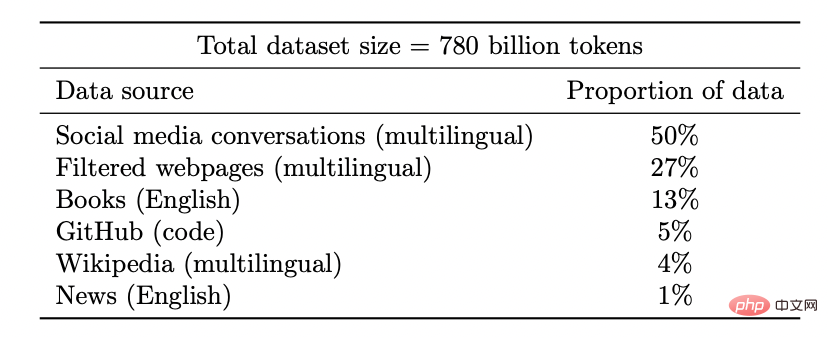
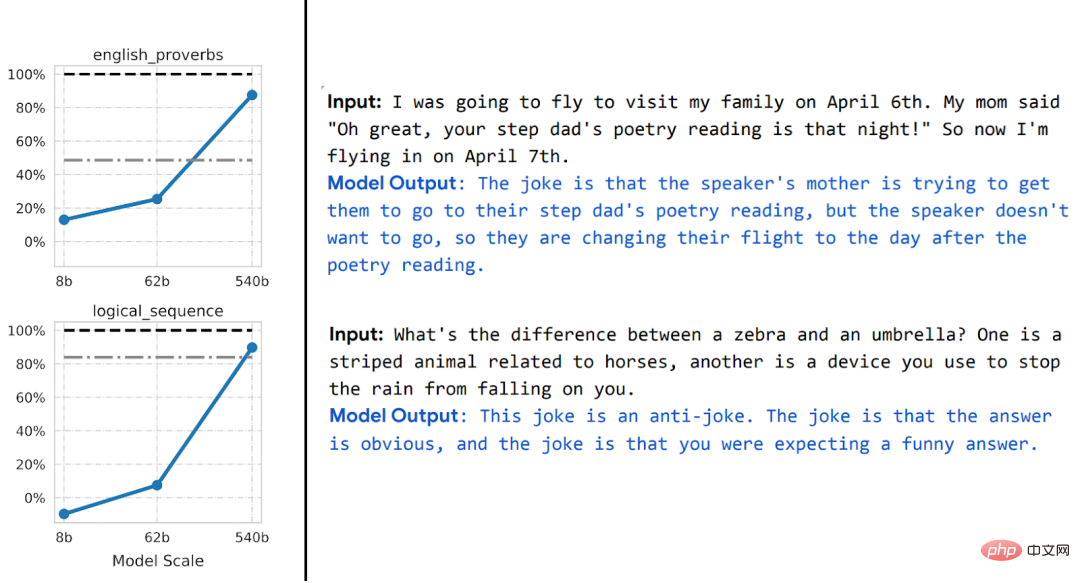
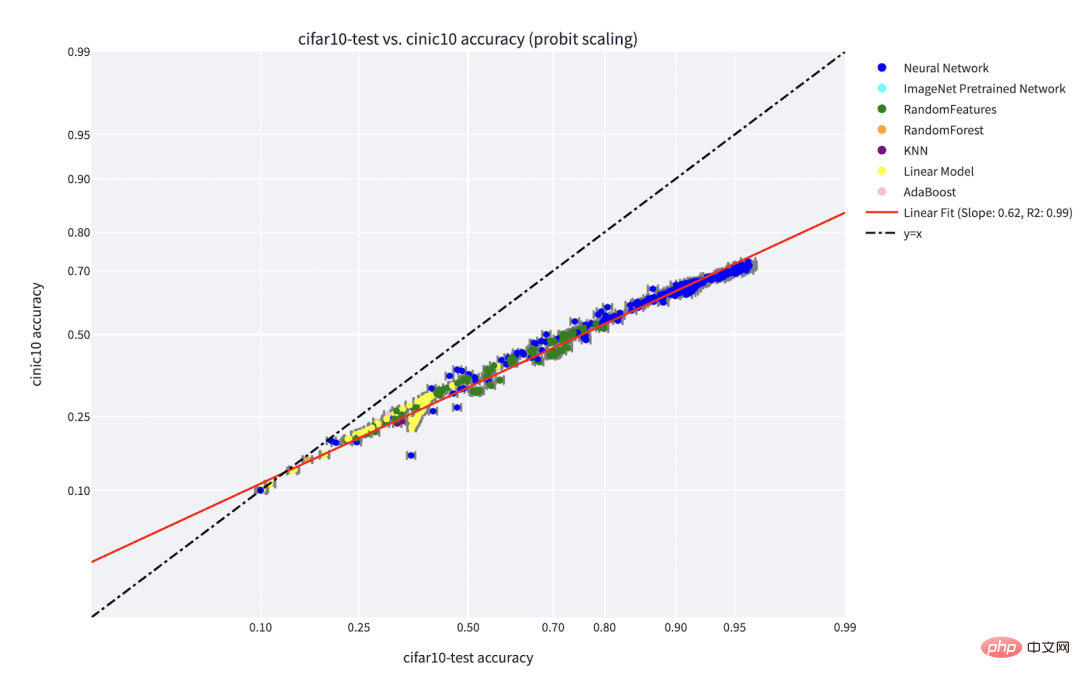
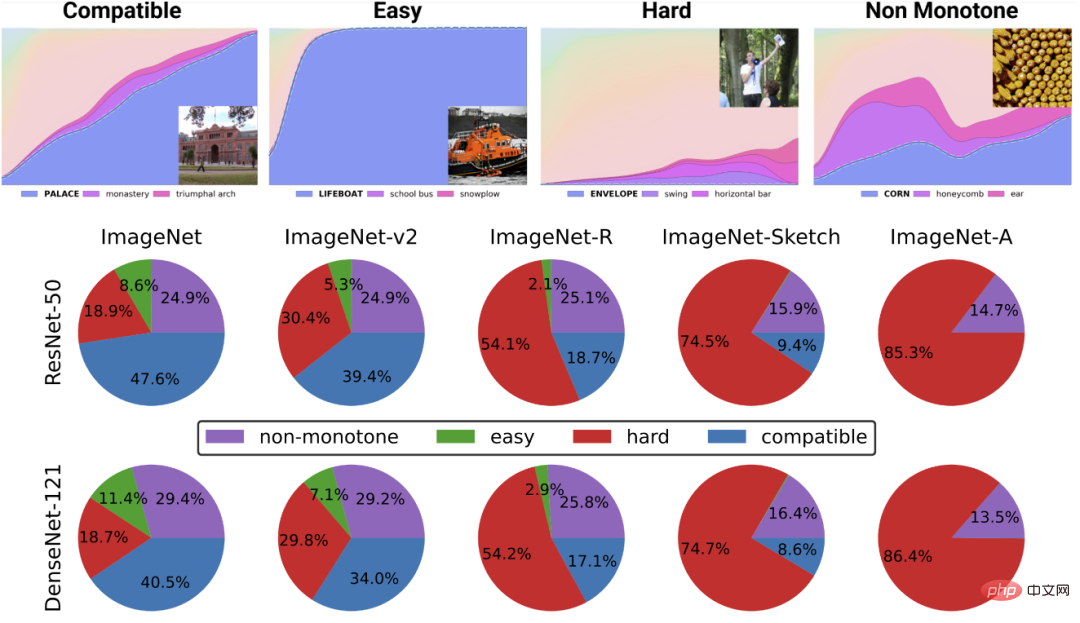
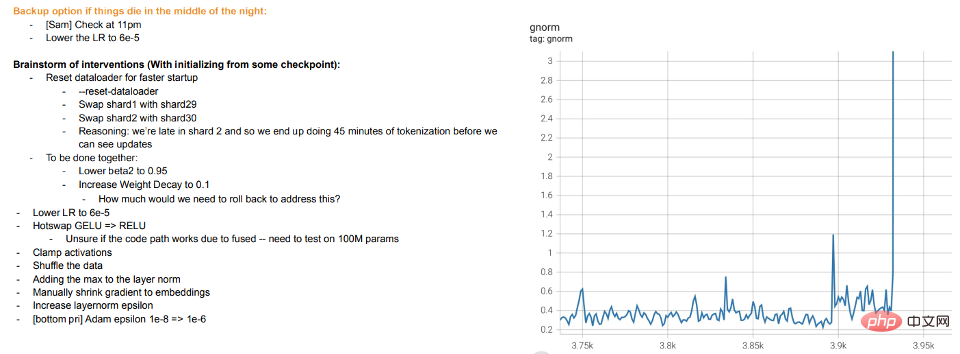

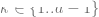 , seseorang boleh "mencantum" lapisan k pertama model d dalam yang dilatih dengan penyeliaan kendiri dengan lapisan d-k terakhir model diselia dan menjadikan prestasi hampir Mengekalkan yang asal tahap.
, seseorang boleh "mencantum" lapisan k pertama model d dalam yang dilatih dengan penyeliaan kendiri dengan lapisan d-k terakhir model diselia dan menjadikan prestasi hampir Mengekalkan yang asal tahap. 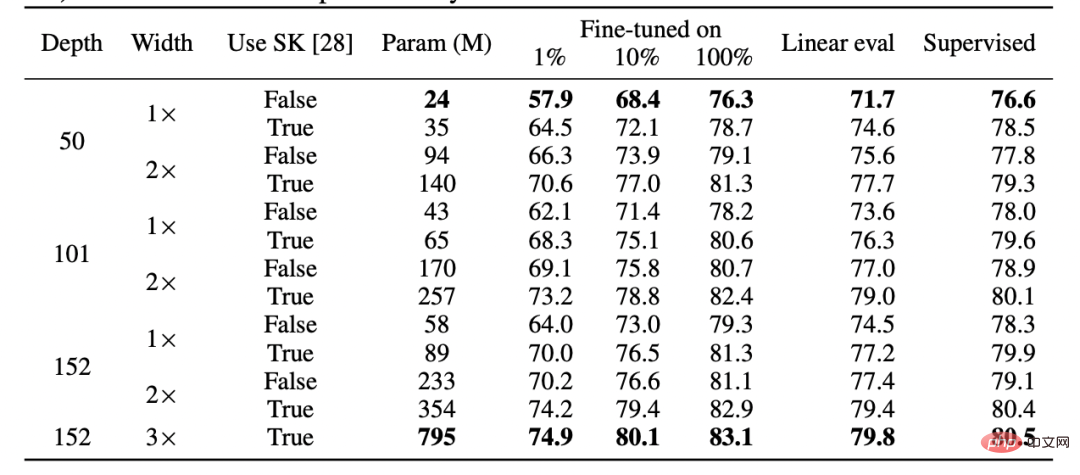
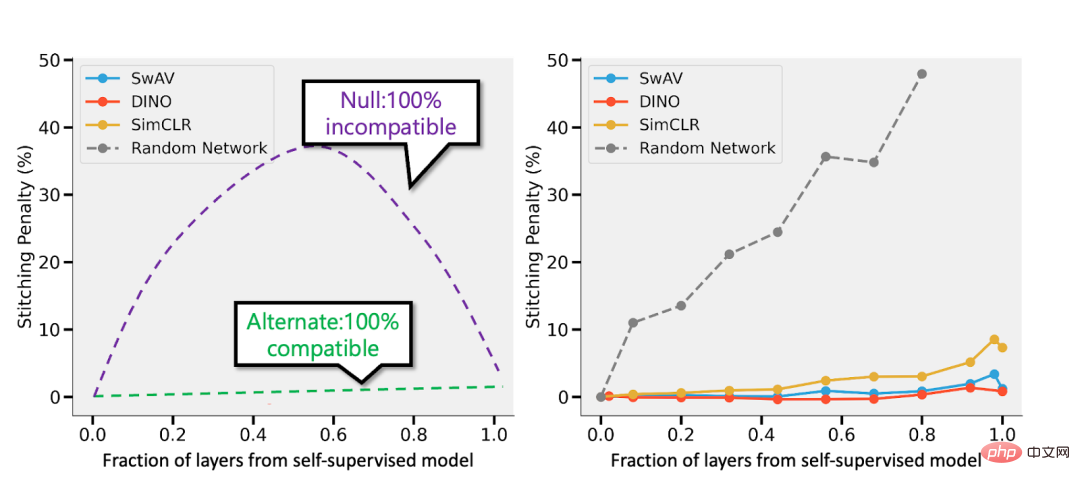
Kes 2: Pengiraan berlebihan
5 Ringkasan
Atas ialah kandungan terperinci Ahli sains komputer teori Boaz Barak: Pembelajaran mendalam bukanlah 'statistik mudah', dan jarak antara keduanya semakin jauh. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

