Ilustrasi sepuluh algoritma pembelajaran mesin yang paling biasa digunakan!

Dalam bidang pembelajaran mesin, terdapat pepatah yang dipanggil "Tiada makan tengah hari percuma di dunia". penting.

Sebagai contoh, anda tidak boleh mengatakan bahawa rangkaian saraf sentiasa lebih baik daripada pepohon keputusan, atau sebaliknya. Pelaksanaan model dipengaruhi oleh banyak faktor, seperti saiz dan struktur set data.

Oleh itu, anda harus mencuba pelbagai algoritma berdasarkan masalah anda, sambil menggunakan set ujian data untuk menilai prestasi dan memilih yang terbaik.

Sudah tentu, algoritma yang anda cuba mesti berkaitan dengan masalah anda, dan kuncinya ialah tugas utama pembelajaran mesin. Sebagai contoh, jika anda ingin membersihkan rumah anda, anda mungkin menggunakan pembersih vakum, penyapu atau mop, tetapi anda tidak akan mengambil penyodok dan mula menggali lubang.

Bagi pendatang baharu dalam pembelajaran mesin yang tidak sabar-sabar untuk memahami asas pembelajaran mesin, berikut ialah sepuluh algoritma pembelajaran mesin terbaik yang digunakan oleh saintis data untuk memperkenalkan ciri-ciri sepuluh algoritma teratas ini supaya semua orang dapat memahami dengan lebih baik dan Permohonan, datang dan lihat.

01 Regresi Linear

Regresi linear mungkin merupakan salah satu algoritma yang paling terkenal dan paling mudah difahami dalam statistik dan pembelajaran mesin.

Memandangkan pemodelan ramalan terutamanya mementingkan meminimumkan ralat model, atau membuat ramalan paling tepat dengan mengorbankan kebolehtafsiran. Kami meminjam, menggunakan semula dan mencuri algoritma daripada pelbagai bidang yang berbeza, dan beberapa pengetahuan statistik terlibat.

Regresi linear diwakili oleh persamaan yang menerangkan hubungan linear antara pembolehubah input (x) dan pembolehubah output (y) dengan mencari berat khusus (B) pembolehubah input.

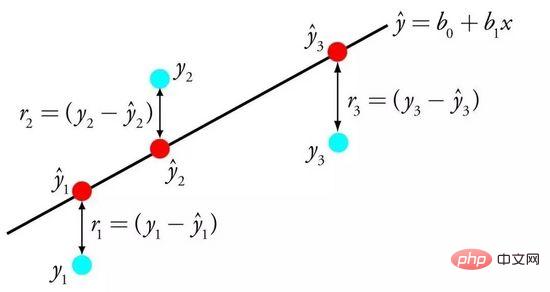
Regression Linear

Contoh: y = B0 + B1 * x

Diberi input x, kami akan meramalkan y, regresi linear The Matlamat algoritma pembelajaran adalah untuk mencari nilai pekali B0 dan B1.

Model regresi linear boleh dipelajari daripada data menggunakan teknik yang berbeza, seperti penyelesaian algebra linear untuk kuasa dua terkecil biasa dan pengoptimuman keturunan kecerunan.

Regresi linear telah wujud selama lebih 200 tahun dan telah dikaji secara meluas. Beberapa peraturan praktikal apabila menggunakan teknik ini adalah untuk mengalih keluar pembolehubah yang hampir serupa (berkorelasi) dan mengeluarkan bunyi daripada data jika boleh. Ini adalah teknik yang cepat dan mudah serta algoritma pertama yang baik.

02 Regresi Logistik

Regresi logistik ialah satu lagi teknik yang dipinjam oleh pembelajaran mesin daripada bidang statistik. Ini adalah kaedah khusus untuk masalah klasifikasi binari (masalah dengan dua nilai kelas).

Regression logistik adalah serupa dengan regresi linear kerana matlamat kedua-duanya adalah untuk mencari nilai berat setiap pembolehubah input. Tidak seperti regresi linear, nilai ramalan output diubah menggunakan fungsi bukan linear yang dipanggil fungsi logistik.

Fungsi logik kelihatan seperti S besar dan menukarkan sebarang nilai ke dalam julat 0 hingga 1. Ini berguna kerana kita boleh menggunakan peraturan yang sepadan dengan output fungsi logistik, mengklasifikasikan nilai kepada 0 dan 1 (contohnya, jika IF kurang daripada 0.5, maka output 1) dan meramalkan nilai kelas.

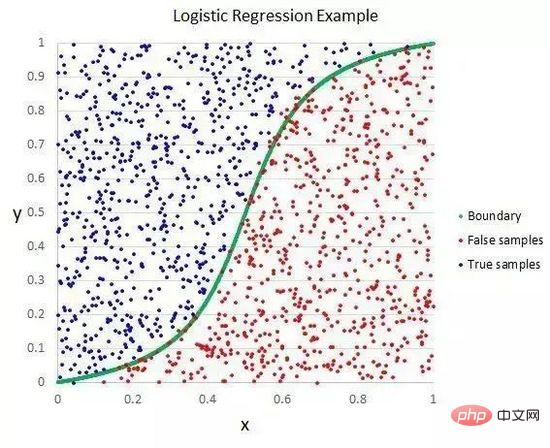
Regression Logistik

Disebabkan kaedah pembelajaran model yang unik, ramalan yang dibuat oleh regresi logistik juga boleh digunakan untuk mengira kebarangkalian tergolong dalam kelas 0 atau kelas 1. Ini berguna untuk masalah yang memerlukan banyak rasional.

Seperti regresi linear, regresi logistik berfungsi lebih baik apabila anda mengalih keluar atribut yang tidak berkaitan dengan pembolehubah output dan atribut yang sangat serupa (berkorelasi) antara satu sama lain. Ini adalah model yang cepat belajar dan berkesan menangani masalah klasifikasi binari.

03 Analisis diskriminasi linear

Regresi logistik tradisional terhad kepada masalah klasifikasi binari. Jika anda mempunyai lebih daripada dua kelas, Analisis Diskriminasi Linear (LDA) ialah teknik pengelasan linear pilihan.

Perwakilan LDA sangat mudah. Ia terdiri daripada sifat statistik data anda, dikira berdasarkan setiap kategori. Untuk pembolehubah input tunggal, ini termasuk:

Nilai min untuk setiap kategori.

Varians dikira merentas semua kategori.

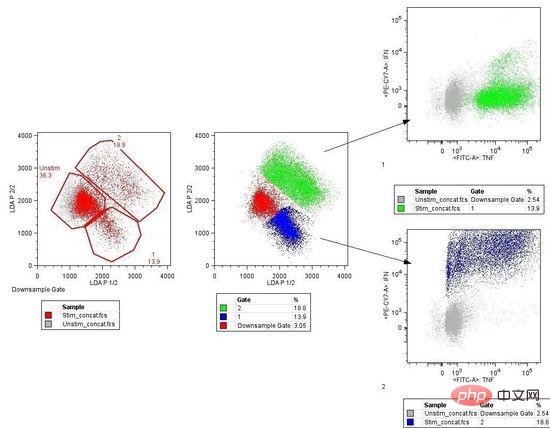
Analisis Diskriminasi Linear

LDA dilakukan dengan mengira nilai diskriminasi setiap kelas dan membuat ramalan untuk kelas dengan nilai maksimum. Teknik ini mengandaikan bahawa data mempunyai taburan Gaussian (lengkung loceng), jadi sebaiknya buang outlier secara manual daripada data terlebih dahulu. Ini adalah pendekatan yang mudah tetapi berkuasa dalam klasifikasi masalah pemodelan ramalan.

04 Pokok Klasifikasi dan Regresi

Pokok keputusan ialah algoritma penting untuk pembelajaran mesin.

Model pokok keputusan boleh diwakili oleh pokok binari. Ya, ia adalah pokok binari daripada algoritma dan struktur data, tiada yang istimewa. Setiap nod mewakili pembolehubah input tunggal (x) dan anak kiri dan kanan pembolehubah itu (dengan andaian pembolehubah ialah nombor).

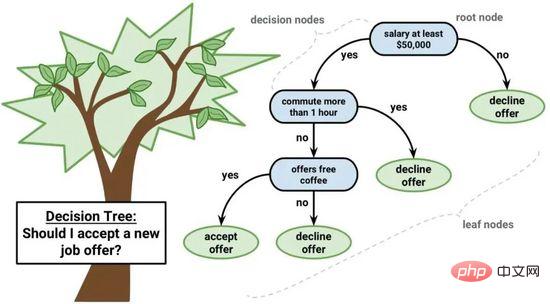
Pokok Keputusan

Nod daun pokok mengandungi pembolehubah keluaran (y) yang digunakan untuk membuat ramalan. Ramalan dilakukan dengan melintasi pokok, berhenti apabila nod daun tertentu dicapai, dan mengeluarkan nilai kelas nod daun.

Pokok keputusan mempunyai kelajuan pembelajaran yang pantas dan kelajuan ramalan yang pantas. Ramalan selalunya tepat untuk banyak masalah, dan anda tidak perlu melakukan sebarang penyediaan khas untuk data tersebut.

05 Naive Bayes

Naive Bayes ialah algoritma pemodelan ramalan yang mudah tetapi sangat berkuasa.

Model terdiri daripada dua jenis kebarangkalian yang boleh dikira terus daripada data latihan anda: 1) kebarangkalian setiap kelas 2) kebarangkalian bersyarat bagi kelas yang diberi setiap nilai x. Setelah dikira, model kebarangkalian boleh digunakan untuk membuat ramalan ke atas data baharu menggunakan teorem Bayes. Apabila data anda adalah berangka, adalah perkara biasa untuk mengandaikan taburan Gaussian (lengkung loceng) supaya kebarangkalian ini boleh dianggarkan dengan mudah.

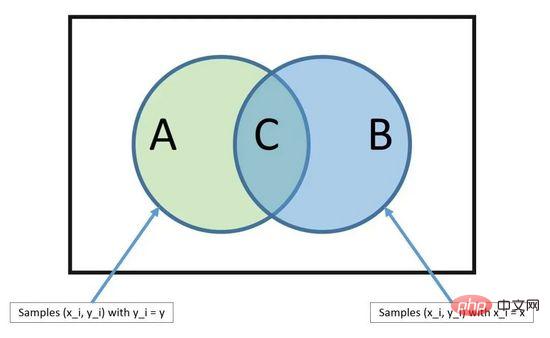
Teorem Bayes

Sebab mengapa Naive Bayes dipanggil naif ialah ia mengandaikan bahawa setiap pembolehubah input adalah bebas. Ini adalah andaian kuat yang tidak realistik untuk data sebenar, tetapi teknik ini masih sangat berkesan untuk masalah kompleks pada skala besar.

06 K Jiran Terdekat

Algoritma KNN sangat mudah dan sangat berkesan. Model KNN diwakili oleh keseluruhan set data latihan. Bukankah ia sangat mudah?

Ramalkan titik data baharu dengan mencari kejadian K yang paling serupa (jiran) dalam keseluruhan set latihan dan meringkaskan pembolehubah output kejadian K ini. Untuk masalah regresi, titik baharu mungkin pembolehubah keluaran min, dan untuk masalah klasifikasi, titik baharu mungkin nilai kategori mod.

Rahsia kejayaan terletak pada menentukan persamaan antara kejadian data. Jika atribut anda semuanya pada skala yang sama, cara paling mudah ialah menggunakan jarak Euclidean, yang boleh dikira terus daripada perbezaan antara setiap pembolehubah input.

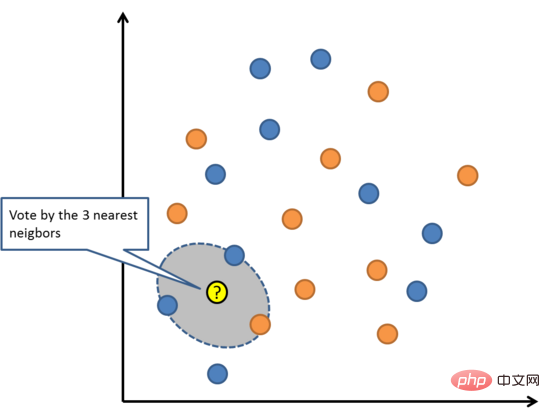
K-Nearest Neighbors

KNN mungkin memerlukan banyak memori atau ruang untuk menyimpan semua data, tetapi pengiraan hanya akan dilakukan apabila ramalan diperlukan (atau belajar). Anda juga boleh mengemas kini dan mengurus set latihan anda pada bila-bila masa untuk mengekalkan ketepatan ramalan.

Konsep jarak atau kedekatan mungkin rosak dalam persekitaran berdimensi tinggi (bilangan besar pembolehubah input), yang boleh memberi kesan negatif kepada algoritma. Peristiwa sedemikian dikenali sebagai sumpahan dimensi. Ia juga membayangkan bahawa anda hanya perlu menggunakan pembolehubah input yang paling relevan untuk meramalkan pembolehubah output.

Kuantiti Vektor Pembelajaran 07

Kelemahan jiran terdekat K ialah anda perlu mengekalkan keseluruhan set data latihan. Kuantiti Vektor Pembelajaran (atau singkatannya LVQ) ialah algoritma rangkaian saraf tiruan yang membolehkan anda menangguhkan sebarang contoh latihan dan mempelajarinya dengan tepat.

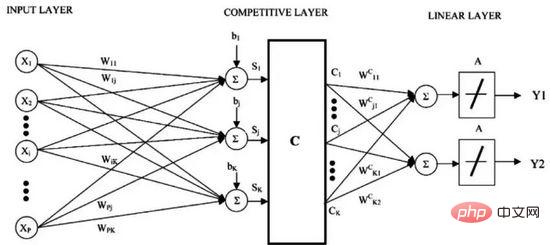
Pembelajaran Kuantiti Vektor

LVQ diwakili oleh koleksi vektor buku kod. Mulakan dengan memilih vektor secara rawak dan kemudian lelaran beberapa kali untuk menyesuaikan diri dengan set data latihan. Selepas belajar, vektor buku kod boleh digunakan untuk ramalan seperti jiran terdekat K. Cari jiran yang paling serupa (padanan terbaik) dengan mengira jarak antara setiap vektor buku kod dan contoh data baharu, kemudian kembalikan nilai kelas unit padanan terbaik atau nilai sebenar dalam kes regresi sebagai ramalan. Keputusan terbaik diperoleh jika anda mengehadkan data kepada julat yang sama (mis. antara 0 dan 1).

Jika anda mendapati KNN memberikan hasil yang baik pada set data anda, cuba gunakan LVQ untuk mengurangkan keperluan memori untuk menyimpan keseluruhan set data latihan.

Mesin Vektor Sokongan 08

Mesin Vektor Sokongan mungkin merupakan salah satu algoritma pembelajaran mesin yang paling popular dan dibincangkan.

Hiperplane ialah garis yang membahagikan ruang pembolehubah input. Dalam SVM, hyperplane dipilih untuk memisahkan titik dalam ruang pembolehubah input mengikut kategorinya (kategori 0 atau kategori 1). Ia boleh dianggap sebagai garis dalam ruang dua dimensi, dan semua titik input boleh dipisahkan sepenuhnya oleh baris ini. Algoritma pembelajaran SVM adalah untuk mencari pekali yang membolehkan hyperplane memisahkan kategori dengan terbaik.

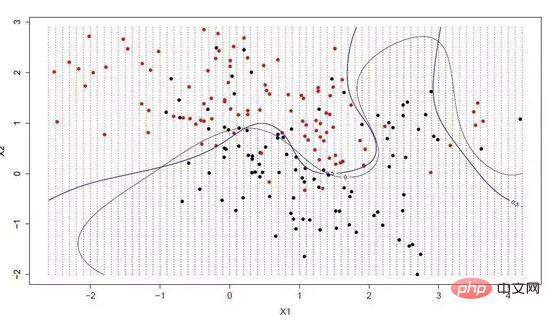
Mesin Vektor Sokongan

Jarak antara hyperplane dan titik data terdekat dipanggil sempadan Hyperplane dengan sempadan terbesar ialah pilihan terbaik. Pada masa yang sama, hanya titik data rapat ini berkaitan dengan definisi hyperplane dan pembinaan pengelas ini dipanggil vektor sokongan, dan ia menyokong atau mentakrifkan hyperplane. Dalam amalan khusus, kami akan menggunakan algoritma pengoptimuman untuk mencari nilai pekali yang memaksimumkan sempadan.

SVM mungkin merupakan salah satu pengelas luar biasa yang paling berkuasa dan patut dicuba pada set data anda.

09 Bagging dan Random Forests

Random Forest ialah salah satu algoritma pembelajaran mesin yang paling popular dan berkuasa. Ia adalah algoritma pembelajaran mesin bersepadu yang dipanggil Bootstrap Aggregation atau Bagging.

Bootstrap ialah kaedah statistik yang berkuasa untuk menganggar kuantiti, seperti min, daripada sampel data. Ia memerlukan sejumlah besar data sampel, mengira purata, dan kemudian purata semua purata untuk mendapatkan anggaran yang lebih tepat bagi purata sebenar.

Kaedah yang sama digunakan dalam pembungkusan, tetapi pokok keputusan paling kerap digunakan dan bukannya menganggarkan keseluruhan model statistik. Ia berbilang sampel data latihan dan kemudian membina model untuk setiap sampel data. Apabila anda perlu membuat ramalan pada data baharu, setiap model membuat ramalan dan membuat purata ramalan untuk mendapatkan anggaran yang lebih baik bagi nilai keluaran sebenar.

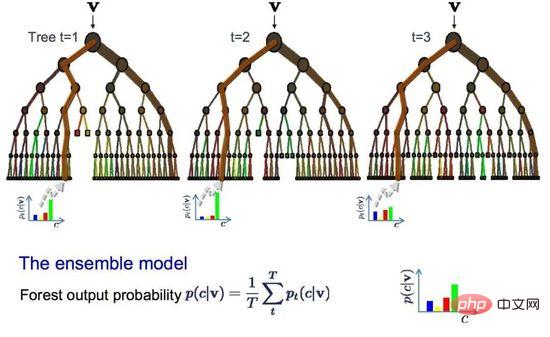
Hutan Rawak

Hutan rawak ialah pelarasan kepada pepohon keputusan Berbanding dengan memilih titik perpecahan terbaik, hutan rawak dicapai dengan memperkenalkan segmentasi suboptimum secara rawak .

Akibatnya, model yang dibuat untuk setiap sampel data akan lebih berbeza antara satu sama lain, tetapi masih tepat dalam pengertiannya sendiri. Menggabungkan keputusan ramalan memberikan anggaran yang lebih baik bagi nilai keluaran potensi yang betul.

Jika anda mendapat hasil yang baik menggunakan algoritma varians tinggi (seperti pepohon keputusan), penambahan algoritma ini akan memberikan anda hasil yang lebih baik.

10 Boosting dan AdaBoost

Boosting ialah teknik ensemble yang mencipta pengelas yang kuat daripada beberapa pengelas yang lemah. Ia mula-mula membina model daripada data latihan dan kemudian mencipta model kedua untuk cuba membetulkan ralat model pertama. Tambah model secara berterusan sehingga set latihan meramalkan dengan sempurna atau telah ditambahkan pada had atas.

AdaBoost ialah algoritma Boosting pertama yang benar-benar berjaya dibangunkan untuk klasifikasi binari, dan ia juga merupakan titik permulaan terbaik untuk memahami Boosting. Algoritma yang paling terkenal pada masa ini dibina berdasarkan AdaBoost ialah peningkatan kecerunan stokastik.

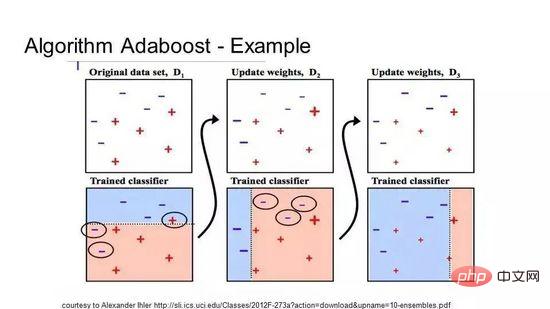
AdaBoost

AdaBoost sering digunakan dengan pepohon keputusan pendek. Selepas pokok pertama dicipta, prestasi setiap contoh latihan pada pokok menentukan berapa banyak perhatian yang perlu diberikan oleh pokok seterusnya kepada contoh latihan itu. Data latihan yang sukar diramal diberi lebih berat, manakala kejadian yang mudah diramal diberi kurang berat. Model dicipta secara berurutan, dan setiap kemas kini model mempengaruhi kesan pembelajaran pepohon seterusnya dalam jujukan. Selepas semua pokok dibina, algoritma membuat ramalan pada data baharu dan menimbang prestasi setiap pokok mengikut ketepatan ia pada data latihan.

Oleh kerana algoritma memberi penekanan yang besar pada pembetulan ralat, data yang bersih tanpa outlier adalah sangat penting.

Soalan biasa yang ditanya oleh pemula apabila berhadapan dengan pelbagai jenis algoritma pembelajaran mesin ialah "Algoritma yang manakah harus saya gunakan?" 🎜>Saiz, kualiti dan sifat data;

Masa pengkomputeran yang tersedia;
• Kepentingan tugasan;
• Apa yang anda mahu lakukan dengan data.
• Malah saintis data yang berpengalaman tidak mempunyai cara untuk mengetahui algoritma mana yang akan berprestasi terbaik sehingga dia mencuba algoritma yang berbeza. Walaupun terdapat banyak algoritma pembelajaran mesin lain, algoritma ini adalah yang paling popular. Jika anda baru dalam pembelajaran mesin, ini adalah tempat yang bagus untuk bermula.

Atas ialah kandungan terperinci Ilustrasi sepuluh algoritma pembelajaran mesin yang paling biasa digunakan!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!