CRPS: Fungsi pemarkahan untuk model pembelajaran mesin Bayesian

Skor Kebarangkalian Kedudukan Berterusan (CRPS) atau "Skor Kebarangkalian Kedudukan Berterusan" ialah fungsi atau statistik yang membandingkan ramalan pengedaran dengan nilai sebenar.

Bahagian penting aliran kerja pembelajaran mesin ialah penilaian model. Proses itu sendiri boleh dianggap akal: bahagikan data kepada set latihan dan ujian, latih model pada set latihan, dan gunakan fungsi pemarkahan untuk menilai prestasinya pada set ujian.

Fungsi pemarkahan (atau metrik) memetakan nilai sebenar dan ramalannya kepada nilai tunggal dan setanding [1]. Contohnya, untuk ramalan berterusan anda boleh menggunakan fungsi pemarkahan seperti RMSE, MAE, MAPE atau R-squared. Bagaimana jika ramalan itu bukan anggaran titik demi titik, tetapi pengedaran?

Dalam pembelajaran mesin Bayesian, ramalan biasanya bukan anggaran yang tepat, sebaliknya pengagihan nilai. Contohnya ramalan boleh dianggarkan parameter taburan, atau dalam kes bukan parametrik, tatasusunan sampel daripada kaedah SKMM.

Dalam kes ini, fungsi pemarkahan tradisional tidak sesuai untuk reka bentuk statistik pengagregatan taburan yang diramalkan ke dalam min atau median menyebabkan kehilangan maklumat yang banyak tentang serakan dan bentuk taburan yang diramalkan.

CRPS

Skor Kebarangkalian Kedudukan Berterusan (CRPS) ialah fungsi pecahan yang membandingkan satu nilai benar kepada fungsi pengedaran kumulatif (CDF):

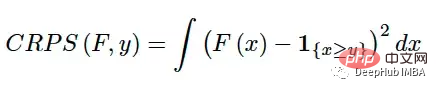
Ia mula diperkenalkan pada tahun 1970-an [4], terutamanya untuk ramalan cuaca, dan kini menerima perhatian baharu dalam kesusasteraan dan industri [1] [6]. Ia boleh digunakan sebagai metrik untuk menilai prestasi model apabila pembolehubah sasaran adalah berterusan dan model meramalkan taburan sasaran termasuk model regresi Bayesian atau siri masa Bayesian [5].

CRPS berguna untuk ramalan parametrik dan bukan parametrik dengan menggunakan CDF: untuk banyak taburan, CRPS [3] mempunyai ungkapan analitikal, dan untuk ramalan bukan parametrik, CRPS menggunakan fungsi taburan kumulatif empirikal (eCDF ).

Selepas mengira CRPS untuk setiap pemerhatian dalam set ujian, anda juga perlu mengagregatkan keputusan menjadi satu nilai. Sama seperti RMSE dan MAE, ia diringkaskan menggunakan min (kemungkinan berwajaran):

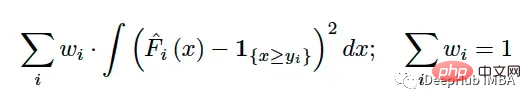
Cabaran utama dalam membandingkan nilai individu dengan taburan ialah bagaimana nilai individu Menukar kepada perwakilan pengedaran. CRPS menyelesaikan masalah ini dengan menukar kebenaran asas kepada taburan merosot dengan fungsi penunjuk. Contohnya, jika nilai sebenar ialah 7, kita boleh menggunakan:

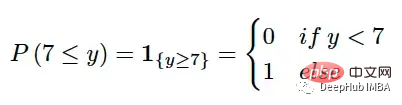
Fungsi penunjuk ialah CDF yang sah dan boleh memenuhi semua keperluan CDF. Taburan yang diramalkan kemudiannya boleh dibandingkan dengan taburan degenerasi nilai sebenar. Kami pasti mahu pengedaran yang diramalkan sehampir mungkin dengan realiti yang mungkin; jadi ini boleh dinyatakan secara matematik dengan mengukur kawasan (kuadrat) antara dua CDF ini:

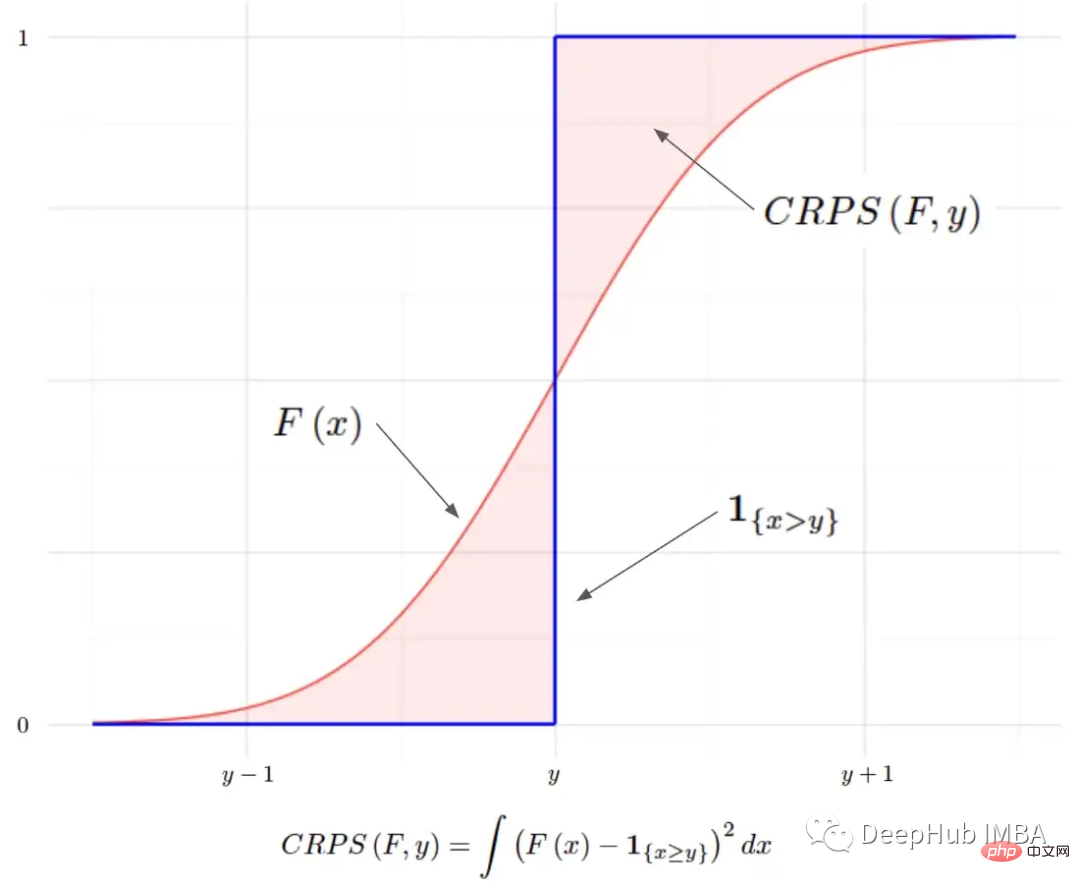
MAE hingga Hubungan MAE

CRPS berkait rapat dengan MAE (Mean Absolute Error) yang terkenal. Jika kita mengambil ramalan secara tepat dan menganggapnya sebagai CDF yang merosot dan menyuntiknya ke dalam persamaan CRPS, kita boleh mendapatkan:

Jadi jika taburan ramalan adalah taburan degenerasi (seperti anggaran titik-bijak), maka CRPS akan dikurangkan kepada MAE. Ini membantu kami memahami CRPS dari perspektif lain: ia boleh dilihat sebagai menggeneralisasikan MAE kepada ramalan pengedaran, atau MAE ialah kes khas CRPS apabila pengedaran ramalan merosot.

Apabila ramalan model ialah taburan parametrik (contohnya, parameter taburan perlu diramalkan), CRPS mempunyai ungkapan analitikal untuk beberapa taburan biasa [3]. Jika model meramalkan parameter μ dan σ bagi taburan normal, CRPS boleh dikira menggunakan formula berikut:

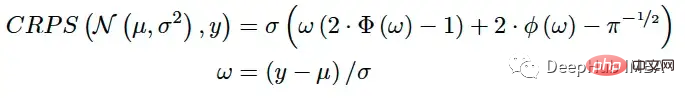
Penyelesaian ini boleh menyelesaikan taburan yang diketahui seperti Beta, Gamma, Logistik, pengedaran lognormal dan lain-lain [3].

Mengira eCDF ialah tugas yang membosankan apabila ramalan bukan parametrik, atau lebih khusus - ramalan ialah satu siri simulasi. Tetapi CRPS juga boleh dinyatakan sebagai:

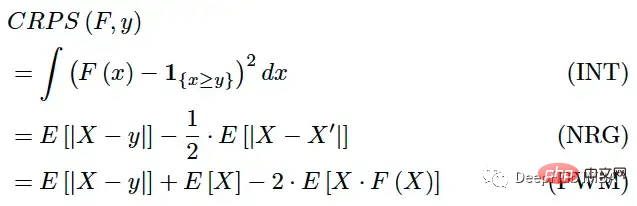
Di mana X, X' adalah F secara bebas dan teragih sama. Ungkapan ini lebih mudah untuk dikira, walaupun ia masih memerlukan sedikit pengiraan.

Python melaksanakan

import numpy as np
 
 
 # Adapted to numpy from pyro.ops.stats.crps_empirical
 # Copyright (c) 2017-2019 Uber Technologies, Inc.
 # SPDX-License-Identifier: Apache-2.0
 def crps(y_true, y_pred, sample_weight=None):
 num_samples = y_pred.shape[0]
 absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
 if num_samples == 1:
 return np.average(absolute_error, weights=sample_weight)
 
 y_pred = np.sort(y_pred, axis=0)
 diff = y_pred[1:] - y_pred[:-1]
 weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1)
 weight = np.expand_dims(weight, -1)
 
 per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2
 return np.average(per_obs_crps, weights=sample_weight)

Fungsi CRPS dilaksanakan mengikut borang NRG [2]. Diadaptasi daripada pyroppl[6]

import numpy as np
 
 
 def crps(y_true, y_pred, sample_weight=None):
 num_samples = y_pred.shape[0]
 absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
 if num_samples == 1:
 return np.average(absolute_error, weights=sample_weight)
 
 y_pred = np.sort(y_pred, axis=0)
 b0 = y_pred.mean(axis=0)
 b1_values = y_pred * np.arange(num_samples).reshape((num_samples, 1))
 b1 = b1_values.mean(axis=0) / num_samples
 
 per_obs_crps = absolute_error + b0 - 2 * b1
 return np.average(per_obs_crps, weights=sample_weight)

Kod di atas melaksanakan CRPS berdasarkan borang PWM[2].

Ringkasan

Skor Kebarangkalian Kedudukan Berterusan (CRPS) ialah fungsi pemarkahan yang membandingkan satu nilai benar dengan taburan ramalannya. Sifat ini menjadikannya relevan dengan pembelajaran mesin Bayesian, di mana model biasanya mengeluarkan ramalan pengedaran dan bukannya anggaran yang tepat. Ia boleh dilihat sebagai generalisasi MAE yang terkenal untuk ramalan pengedaran.

Ia mempunyai ungkapan analitikal untuk ramalan parametrik dan membenarkan pengiraan mudah untuk ramalan bukan parametrik. CRPS boleh menjadi kaedah standard baharu untuk menilai prestasi model pembelajaran mesin Bayesian dengan objektif berterusan.

Atas ialah kandungan terperinci CRPS: Fungsi pemarkahan untuk model pembelajaran mesin Bayesian. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!