Kelajuan pensampelan Resapan Stabil meningkat dua kali ganda! Algoritma pensampelan model resapan hanya dalam 10 hingga 25 langkah

Mengenai perkembangan paling berpengaruh dalam bidang AI tahun ini, pemetaan AI yang meletup pastinya salah satu daripadanya. Pereka bentuk hanya perlu memasukkan perihalan teks imej, dan AI akan menjana imej resolusi tinggi dengan kualiti yang sangat tinggi. Pada masa ini, model yang paling banyak digunakan ialah model sumber terbuka StabilityAI Stable Diffusion Sebaik sahaja model itu bersumberkan terbuka, ia menyebabkan perbincangan meluas dalam komuniti.

Walau bagaimanapun, masalah terbesar dalam menggunakan model resapan ialah kelajuan pensampelannya yang sangat perlahan. Persampelan model perlu bermula daripada gambar hingar tulen dan denoise berterusan langkah demi langkah untuk mendapatkan gambar yang jelas. Dalam proses ini, model mesti mengira sekurang-kurangnya 50 hingga 100 langkah secara bersiri untuk mendapatkan imej berkualiti tinggi. Ini menyebabkan masa yang diperlukan untuk menghasilkan imej adalah 50 hingga 100 kali ganda daripada model generasi dalam yang lain, yang sangat mengehadkan model. penempatan dan pelaksanaan.

Untuk mempercepatkan pensampelan model resapan, ramai penyelidik bermula dari perspektif pengoptimuman perkakasan Contohnya, Google menggunakan bahasa JAX untuk menyusun dan menjalankan model pada TPU, dan pasukan OneFlow [1] menggunakan dibangunkan sendiri Pengkompil mencapai "output imej dalam satu saat" dengan Resapan Stabil. Kaedah ini adalah berdasarkan algoritma pensampelan 50 langkah PNDM [2], yang mempunyai penurunan mendadak dalam kesan pensampelan apabila bilangan langkah dikurangkan.

Baru beberapa hari yang lalu, rekod ini telah ditetapkan semula! Kemas kini Demo[3] rasmi Stable Diffusion menunjukkan bahawa masa untuk mencuba 8 imej telah dipendekkan terus daripada 8 saat asal kepada 4 saat! Ia dua kali lebih pantas!

Pasukan OneFlow, yang berasaskan teknologi pengkompil pembelajaran mendalam yang dibangunkan sendiri, telah berjaya mengubah "OneFlow" sebelumnya tanpa mengurangkan kesan pensampelan . "Gambar akan muncul dalam beberapa saat" telah dipendekkan kepada "Gambar akan muncul dalam setengah saat"! Dapatkan imej definisi tinggi dalam masa kurang daripada 0.5 saat pada GPU! Kerja berkaitan telah diterbitkan dalam [1].

Malah, teras penggerak kerja-kerja ini datang daripada DPM-Solver yang dicadangkan oleh pasukan TSAIL yang diketuai oleh Profesor Zhu Jun dari Universiti Tsinghua, penyelesai cekap yang direka khas untuk model penyebaran Penapis: Algoritma ini tidak memerlukan sebarang latihan tambahan, sesuai untuk kedua-dua model resapan masa diskret dan masa berterusan, hampir boleh menumpu dalam 20 hingga 25 langkah, dan boleh mendapatkan pensampelan yang sangat berkualiti tinggi dalam hanya 10 hingga 15 langkah. Pada Resapan Stabil, Penyelesai DPM 25 langkah boleh mencapai kualiti pensampelan yang lebih baik daripada PNDM 50 langkah, jadi kelajuan pensampelan digandakan secara langsung!

Pautan projek:

• DPM-Solver: Penyelesai ODE Pantas untuk Persampelan Model Probabilistik Resapan dalam Sekitar 10 Langkah: https: //arxiv.org/abs/2206.00927 (NeurIPS 2022 Oral)
• DPM-Solver++: Penyelesai Pantas untuk Persampelan Berpandu Model Probabilistik Resapan: https://arxiv.org/abs/ 2211.01095
• Kod sumber terbuka projek: https://github.com/LuChengTHU/dpm-solver
• Projek dalam talian demo: https:/ / huggingface.co/spaces/LuChengTHU/dpmsolver_sdm

Takrifan dan kaedah pensampelan model resapan

Model resapan mentakrifkan proses ke hadapan yang menambah secara berterusan hingar. Gambar secara beransur-ansur berubah menjadi hingar Gaussian, dan kemudian proses terbalik ditakrifkan untuk secara beransur-ansur menyahbunyi Gaussian menjadi gambaran yang jelas untuk mendapatkan sampel:

Semasa proses pensampelan, model resapan boleh dibahagikan kepada dua kategori mengikut sama ada bunyi tambahan ditambah: satu ialah model persamaan pembezaan stokastik resapan (SDE resapan), dan satu lagi ialah persamaan pembezaan biasa resapan (ODE resapan) . Fungsi objektif latihan kedua-dua model adalah sama, melatih "rangkaian ramalan hingar" dengan meminimumkan ralat kuasa dua min dengan hingar:

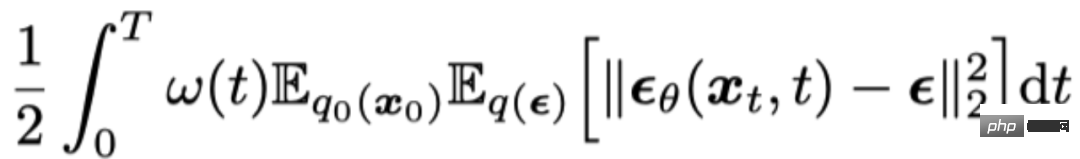
Berdasarkan Proses pensampelan SDE Diffusion boleh dianggap sebagai mendiskrisikan persamaan pembezaan stokastik berikut:

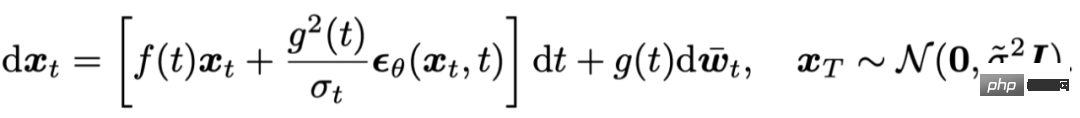
Dan terbukti dalam [4] bahawa DDPM[5 ] ialah pendiskretan tertib pertama SDE di atas.

Proses pensampelan berdasarkan ODE Difusi boleh dianggap sebagai mendiskrisikan persamaan pembezaan biasa berikut:

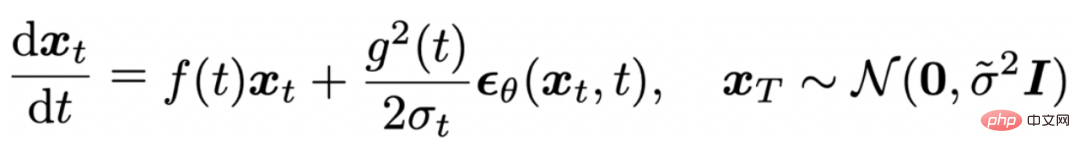
Dan dibuktikan dalam [6] bahawa DDIM[7] ialah pendiskretan tertib pertama bagi ODE di atas.

Walau bagaimanapun, kaedah pendiskretan tertib pertama ini bertumpu dengan sangat perlahan, dan pensampelan model resapan biasanya memerlukan 100 hingga 1000 pengiraan bersiri untuk mendapatkan gambar berkualiti tinggi. Biasanya, untuk mempercepatkan pensampelan model resapan, penyelidik sering menggunakan penyelesai tertib tinggi untuk Diffusion ODE untuk mempercepatkan proses, seperti kaedah Runge-Kutta klasik (RK45 Ini kerana ODE tidak membawa kerawak tambahan). ., saiz langkah pendiskretan boleh menjadi lebih besar. Selepas diberi penyelesaian pada masa s, kaedah Runge-Kutta adalah berdasarkan pendiskretan kamiran berikut:

Pendiskretan sedemikian merawat Resapan ODE secara keseluruhan Kotak hitam kehilangan maklumat ODE yang diketahui dan sukar untuk menumpu dalam kurang daripada 50 langkah.

DPM-Solver: penyelesai yang direka khas untuk model resapan

DPM-Solver adalah berdasarkan struktur separa linear Diffusion ODE, melalui Pengiraan yang tepat dan analitikal istilah linear dalam ODE, kita boleh mendapatkan:

Selebihnya sebutan kamiran ialah kamiran kompleks berkenaan dengan masa. Walau bagaimanapun, pencadang DPM-Solver mendapati bahawa kamiran ini boleh diperolehi dalam bentuk yang sangat mudah dengan menggantikan log-SNR (nisbah isyarat-kepada-bunyi log):

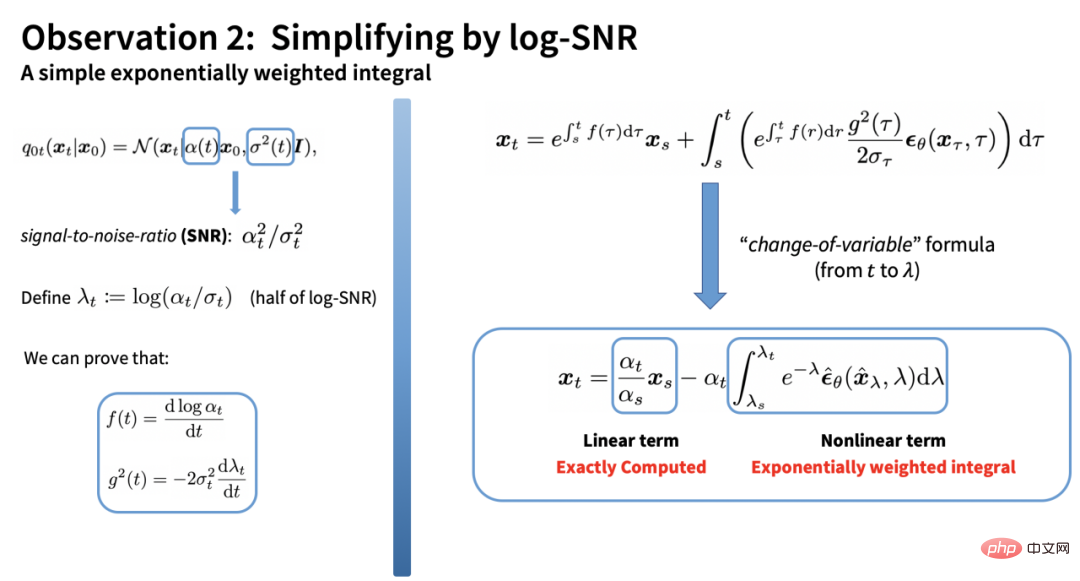
Kamiran selebihnya ialah kamiran berwajaran eksponen berkenaan dengan model ramalan hingar. Dengan melakukan pengembangan Taylor pada model ramalan hingar, kita boleh mendapatkan anggaran kamiran:

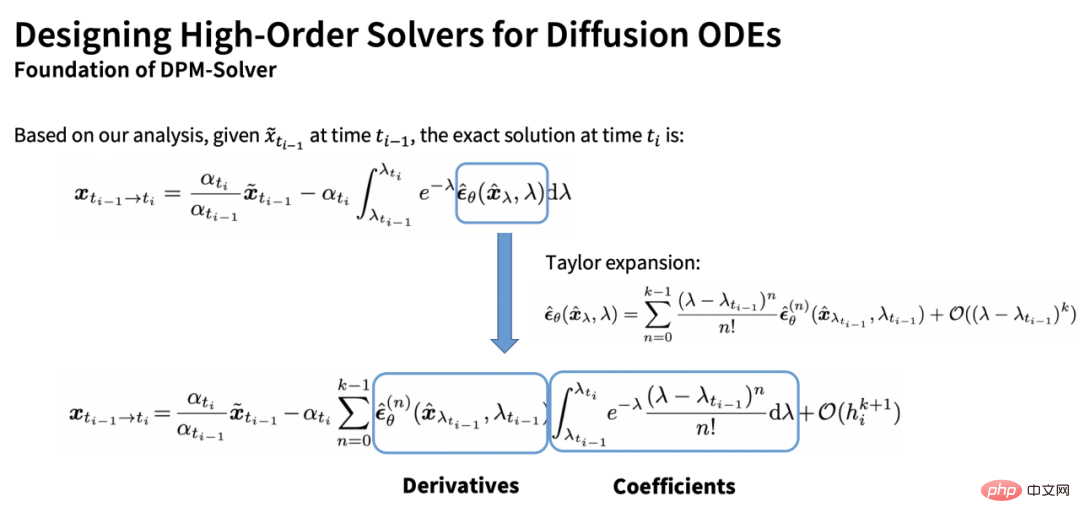
Terdapat dua item dalam anggaran ini: satu ialah penuh Bahagian terbitan (vektor) dan istilah lain ialah bahagian pekali (skalar). Satu lagi sumbangan teras DPM-Solver ialah pekali boleh dikira secara analitikal dengan menyepadukan mengikut bahagian:

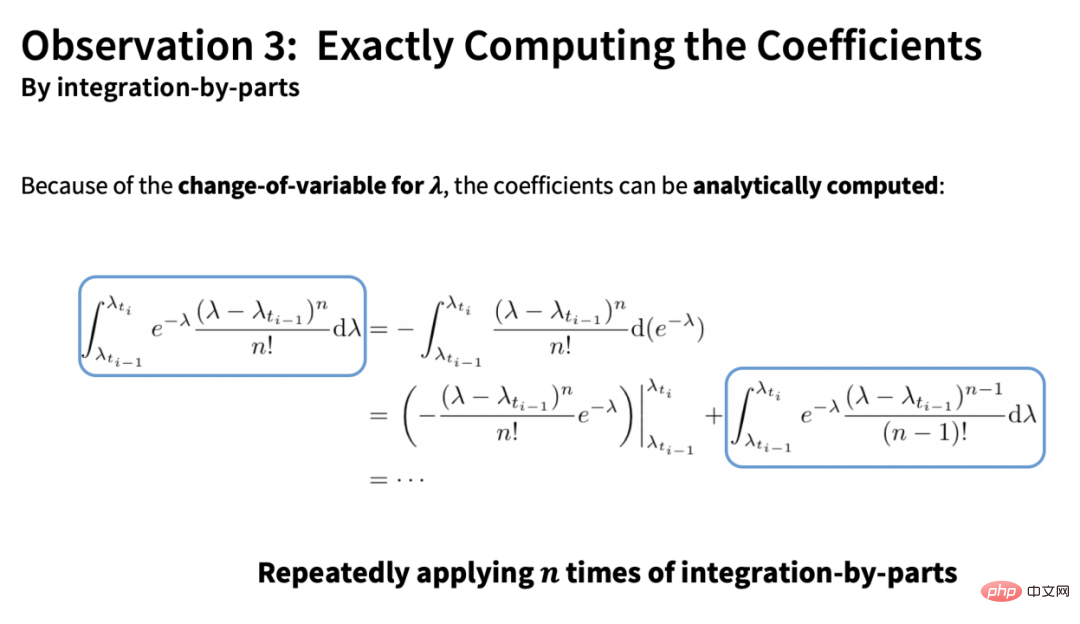
manakala baki jumlah bahagian terbitan ialah Ia boleh dianggarkan dengan kaedah berangka penyelesai ODE tradisional (tanpa sebarang operasi terbitan):

Berdasarkan 4 mata di atas, DPM-Solver melakukan Untuk mengira semua istilah yang diketahui setepat mungkin, hanya bahagian rangkaian saraf yang dianggarkan, dengan itu meminimumkan ralat pendiskretan:

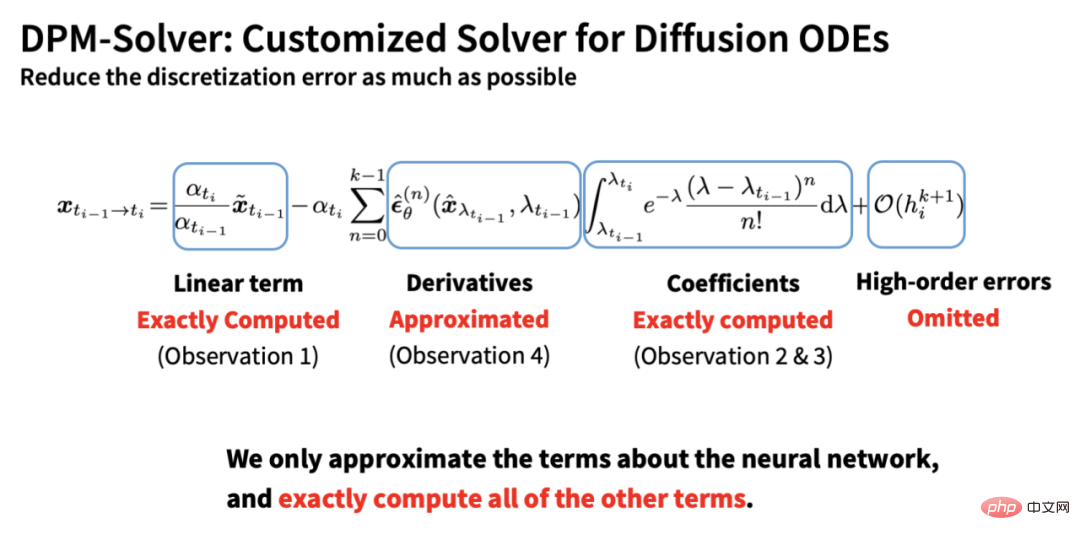
Selain itu, berdasarkan derivasi ini, kita boleh mendapat bahawa DDIM pada asasnya ialah bentuk tertib pertama DPM-Solver, yang juga boleh menjelaskan mengapa DDIM masih boleh mencapai kesan pecutan yang baik apabila bilangan langkah adalah kecil:

Dalam percubaan, DPM-Solver mencapai kesan pecutan jauh melebihi algoritma pensampelan lain, dan ia hampir menumpu hanya dalam 15-20 langkah:

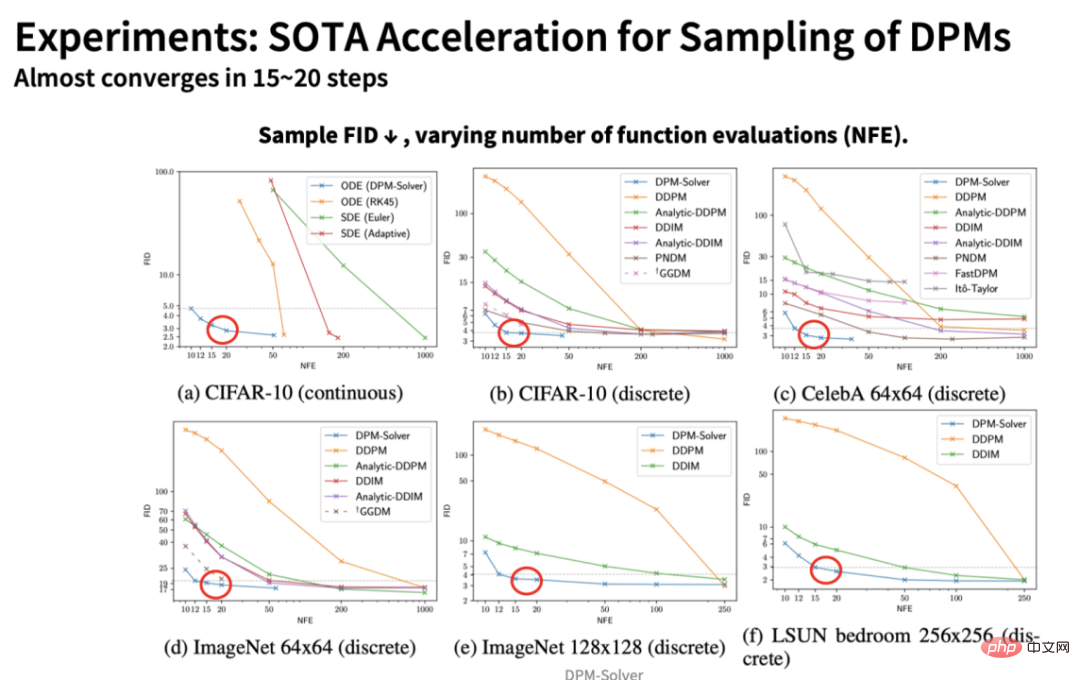
Dan keputusan kuantitatif dalam kertas menunjukkan bahawa jumlah pengiraan tambahan yang diperkenalkan oleh DPM-Solver adalah diabaikan sepenuhnya, iaitu, kesan pecutan pada bilangan langkah adalah berkadar terus dengan kesan pecutan pada masa - oleh itu , berdasarkan 25 langkah Kelajuan pensampelan model DPM-Solver dan Stabil-Diffusion digandakan secara langsung! Sebagai contoh, rajah di bawah menunjukkan kesan algoritma pensampelan yang berbeza pada Stable-Diffusion apabila bilangan langkah berubah Dapat dilihat bahawa DPM-Solver boleh memperoleh pensampelan yang sangat berkualiti dalam 10 hingga 15 langkah:

Menggunakan DPM-Solver

Penggunaan DPM-Solver adalah sangat mudah ia boleh berdasarkan kod rasmi yang disediakan oleh pengarang, atau anda boleh menggunakan pustaka Diffusers arus perdana. Sebagai contoh, berdasarkan kod rasmi yang diberikan oleh pengarang (https://github.com/LuChengTHU/dpm-solver), hanya 3 baris diperlukan:

Kod rasmi menyokong empat model resapan:

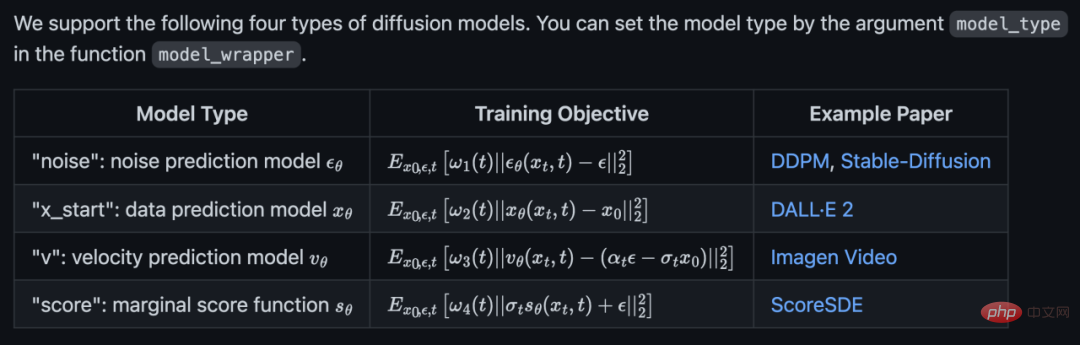
dan juga menyokong pensampelan tanpa syarat, panduan pengelas dan panduan tanpa pengelas:

DPM-Solver berdasarkan perpustakaan Diffusers juga sangat mudah Anda hanya perlu mentakrifkan penjadual:

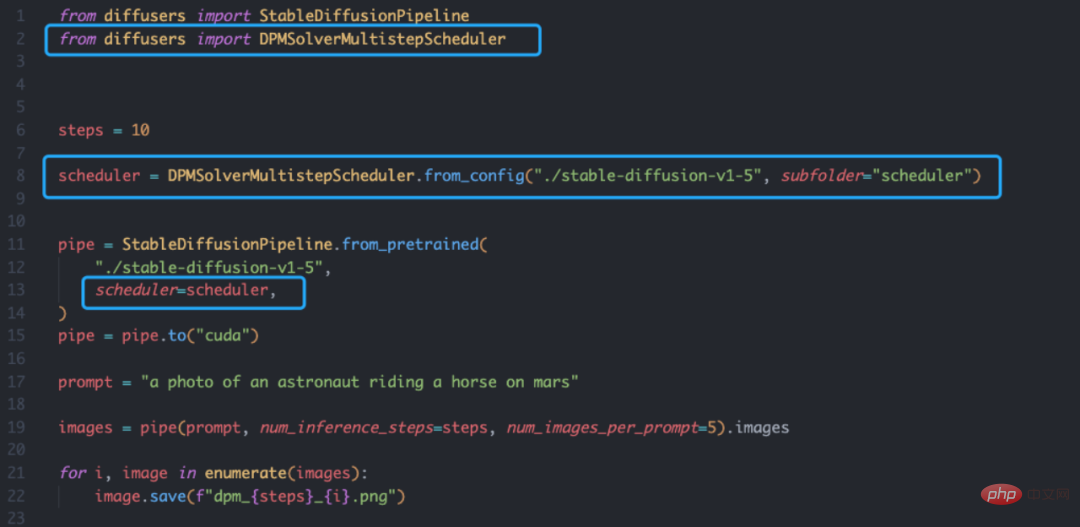
Selain itu, pasukan pengarang juga menyediakan Demo dalam talian: https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm

The gambar di bawah ialah 15 langkah Contohnya, anda boleh melihat bahawa kualiti imej sudah sangat tinggi:

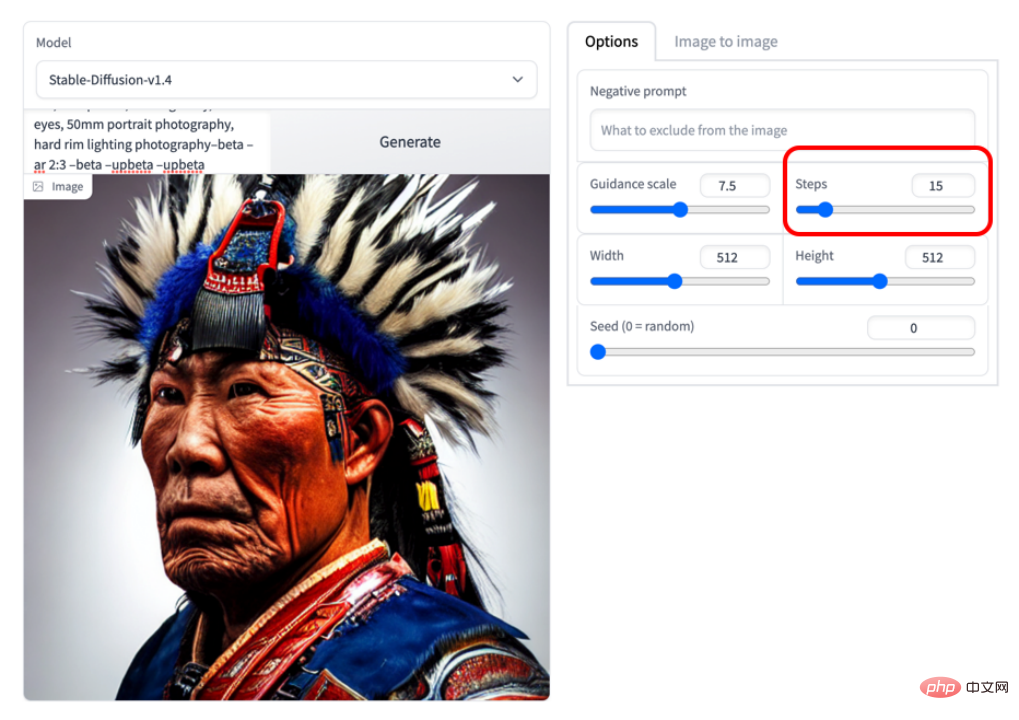
Saya percaya bahawa berdasarkan DPM-Solver, kelajuan pensampelan model resapan tidak lagi menjadi halangan.

Mengenai pengarang

Pengarang pertama kertas DPM-Solver ialah Dr. Lu Cheng dari pasukan TSAIL Universiti Tsinghua Dia juga menulis dalam perbincangan tentang model resapan pada Zhihu Pengenalan pengenalan kepada prinsip model resapan, pada masa ini mempunyai 2000 + suka: https://www.zhihu.com/question/536012286/answer/2533146567

Pasukan TSAIL Universiti Tsinghua Ia telah lama komited kepada penyelidikan teori dan algoritma pembelajaran mesin Bayesian Ia adalah salah satu pasukan terawal di dunia yang mengkaji model penjanaan probabilistik yang mendalam. Ia telah mencapai hasil penyelidikan yang sistematik dan mendalam dalam Bayesian model, algoritma cekap dan perpustakaan pengaturcaraan kemungkinan. Seorang lagi pelajar kedoktoran dalam pasukan, Bao Fan, mencadangkan Analytic-DPM [8][9], yang menyediakan bentuk analisis yang mudah dan mengejutkan untuk min dan varians optimum model resapan, dan memenangi Anugerah Kertas Cemerlang ICLR 2022. Dari segi pengaturcaraan kebarangkalian, Machine Heart melaporkan pustaka pengaturcaraan kebarangkalian mendalam "ZhuSuan" yang dikeluarkan oleh pasukan seawal 2017 (https://zhusuan.readthedocs.io/en/latest/) [10], yang merupakan yang paling awal di dunia Salah satu perpustakaan pengaturcaraan untuk model probabilistik dalam. Di samping itu, perlu dinyatakan bahawa dua pengarang teras model kebarangkalian penyebaran, Song Yang dan Song Jiaming, kedua-duanya menerima latihan penyelidikan saintifik di bawah bimbingan Profesor Zhu Jun sebagai mahasiswa, dan kemudiannya pergi ke Universiti Stanford untuk belajar untuk ijazah kedoktoran. . Pengarang bersama kertas kerja, Zhou Yuhao, Chen Jianfei, dan Li Chongxuan, juga merupakan pelajar kedoktoran yang cemerlang yang dilatih oleh kumpulan TSAIL Zhou Yuhao ialah seorang pelajar di Jabatan Komputer Universiti Tsinghua dan Hillhouse School of Artificial Intelligence Universiti Renmin masing-masing.

Atas ialah kandungan terperinci Kelajuan pensampelan Resapan Stabil meningkat dua kali ganda! Algoritma pensampelan model resapan hanya dalam 10 hingga 25 langkah. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!