Kemajuan terkini dalam model jarang! Ma Yi + LeCun bergabung tenaga: "Kotak putih" pembelajaran tanpa pengawasan

Baru-baru ini Profesor Ma Yi dan pemenang Anugerah Turing Yann LeCun bersama-sama menerbitkan kertas kerja di ICLR 2023, yang menerangkan kaedah pembelajaran tanpa pengawasan yang minimalis dan boleh ditafsir yang tidak memerlukan penggunaan penambahan data, pelarasan hiperparameter atau reka bentuk kejuruteraan lain, anda boleh mencapai prestasi hampir dengan kaedah SSL SOTA.

Pautan kertas: ​https://arxiv.org/abs/2209.15261​

Kaedah ini menggunakan transformasi manifold jarang dan menggabungkan pengekodan jarang, pembelajaran manifold dan analisis ciri perlahan.

Menggunakan transformasi manifold jarang deterministik satu lapisan, ia boleh mencapai 99.3% ketepatan 1 teratas KNN pada MNIST dan 81.1% ketepatan 1 teratas KNN pada Ketepatan CIFAR-10, ia boleh mencapai 53.2% KNN top-1 ketepatan pada CIFAR-100.

Melalui peningkatan skala kelabu yang ringkas, ketepatan model masing-masing mencapai 83.2% dan 57% pada CIFAR-10 dan CIFAR-100. Keputusan ini mengecilkan kaedah "kotak putih" yang mudah dan kaedah SOTA.

Selain itu, artikel ini juga menyediakan penjelasan visual tentang cara membentuk transformasi perwakilan tanpa pengawasan. Kaedah ini berkait rapat dengan kaedah penyeliaan sendiri pembenaman terpendam dan boleh dianggap sebagai kaedah VICReg yang paling mudah.

Walaupun masih terdapat jurang prestasi kecil antara model konstruktif mudah kami dan pendekatan SOTA, terdapat Bukti menunjukkan bahawa ini adalah hala tuju yang menjanjikan untuk mencapai pendekatan berprinsip, kotak putih kepada pembelajaran tanpa pengawasan.

Pengarang pertama artikel itu, Yubei Chen, ialah pembantu pasca doktoral di Pusat Sains Data (CDS) dan Penyelidikan Kepintaran Buatan Asas (FAIR) di New York University penyelia ialah Profesor Yann LeCun Beliau berkelulusan Ph.D dari California The Redwood Center for Theoretical Neuroscience dan Berkeley Artificial Intelligence Institute (BAIR) di University of Berkeley.

Hal tuju penyelidikan utama ialah persimpangan pembelajaran neurosains pengiraan dan hasil penyelidikan tanpa pengawasan (self-supervised). Pemahaman yang dipertingkatkan tentang prinsip pengiraan pembelajaran perwakilan tanpa pengawasan dalam otak dan mesin, dan membentuk semula pengetahuan tentang statistik isyarat semula jadi.

Profesor Ma Yi menerima ijazah sarjana muda berganda dalam automasi dan matematik gunaan dari Universiti Tsinghua pada tahun 1995, ijazah sarjana dalam EECS dari University of California, Berkeley pada tahun 1997, dan ijazah sarjana. dalam matematik dan EECS pada tahun 2000 Ph.D. Beliau kini merupakan profesor di Jabatan Kejuruteraan Elektrik dan Sains Komputer di University of California, Berkeley, dan juga Felo IEEE, Felo ACM, dan Felo SIAM.

Yann LeCun terkenal dengan kerjanya menggunakan rangkaian saraf konvolusi (CNN) dalam pengecaman aksara optik dan penglihatan komputer. Beliau juga dikenali sebagai bapa rangkaian konvolusi; Bengio dan Hinton bersama-sama memenangi Anugerah Turing, anugerah tertinggi dalam sains komputer.

Bermula daripada pembelajaran tanpa pengawasan yang paling mudah

Dalam beberapa tahun kebelakangan ini, pembelajaran perwakilan tanpa pengawasan telah mencapai kemajuan yang besar dan dijangka akan digunakan dalam mesin dipacu data skalabiliti yang kuat dalam pembelajaran.

Walau bagaimanapun, apakah representasi yang dipelajari dan bagaimana sebenarnya ia dibentuk dengan cara yang tidak diawasi masih tidak jelas, selain itu, sama ada terdapat satu set alat untuk menyokong semua prinsip Bersama yang tidak diselia ini perwakilan masih tidak jelas.

Ramai penyelidik telah menyedari kepentingan meningkatkan pemahaman model dan telah mengambil beberapa langkah perintis untuk cuba memudahkan kaedah SOTA, mewujudkan hubungan dengan kaedah klasik, dan menyatukan Kaedah yang berbeza untuk menggambarkan representasi dan menganalisis ini dari perspektif teori, dengan harapan untuk membangunkan teori pengiraan yang berbeza: satu yang membolehkan kita membina "kotak putih" yang mudah dan boleh ditafsir sepenuhnya daripada data berdasarkan model prinsip pertama, teori itu juga boleh memberikan panduan untuk memahami prinsip pembelajaran tanpa pengawasan dalam otak manusia.

Dalam kerja ini, penyelidik mengambil satu lagi langkah kecil ke arah matlamat ini, cuba membina model pembelajaran tanpa pengawasan "kotak putih" paling mudah yang tidak memerlukan rangkaian dalam, kepala unjuran, penambahan Data atau pelbagai reka bentuk kejuruteraan lain.

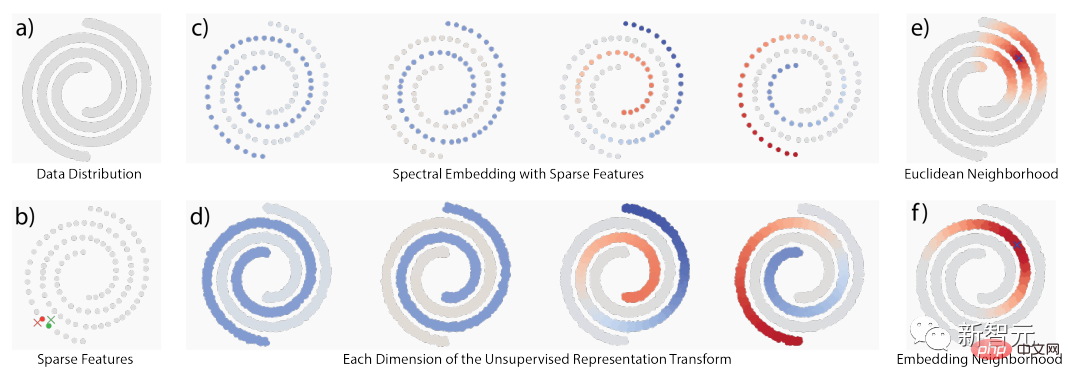
Artikel ini menggunakan dua prinsip pembelajaran tanpa pengawasan klasik, iaitu pembenaman sparsity dan spectral, model dua lapisan telah dibina dan mencapai hasil penanda aras yang tidak penting pada beberapa set data standard.

Hasil eksperimen menunjukkan bahawa model dua lapisan berdasarkan transformasi manifold jarang mempunyai objektif yang sama dengan kaedah penyeliaan kendiri yang dibenamkan terpendam dan berfungsi dengan baik tanpa sebarang peningkatan data , ia mencapai ketepatan tahap 1 tertinggi bagi KNN sebanyak 99.3% pada MNIST, 81.1% daripada ketepatan tahap 1 tertinggi bagi KNN pada CIFAR-10, dan ketepatan 53.2% pada CIFAR-100.

Melalui peningkatan skala kelabu yang mudah, kami terus mencapai ketepatan 83.2% atas-1 KNN pada CIFAR-10 dan 57% ketepatan atas-1 KNN pada CIFAR-100.

Hasil ini mengambil langkah penting ke arah merapatkan jurang antara model "kotak putih" dan model SOTA seliaan sendiri (SSL) Walaupun jurang itu masih jelas, para penyelidik percaya lagi Menutup jurang memungkinkan untuk memperoleh pemahaman yang lebih mendalam tentang pembelajaran perwakilan tanpa pengawasan, yang juga merupakan garis penyelidikan yang menjanjikan ke arah aplikasi praktikal teori ini.

Tiga soalan asas

Apakah yang dimaksudkan dengan pembentangan semula tanpa pengawasan (sendiri)

Pada asasnya, sebarang transformasi bukan identiti bagi isyarat asal boleh dipanggil perwakilan (pembentangan semula), tetapi komuniti akademik lebih berminat dengan mereka yang berguna.

Matlamat makro pembelajaran pembentangan semula tanpa pengawasan adalah untuk mencari fungsi yang mengubah data asal kepada ruang baharu supaya perkara "serupa" diletakkan lebih rapat ;Pada masa yang sama , ruang baru tidak boleh runtuh dan remeh, iaitu, struktur geometri atau rawak data mesti dipelihara.

Jika matlamat ini tercapai, maka kandungan "tidak serupa" secara semula jadi akan diletakkan jauh dalam ruang perwakilan.

Dari mana datangnya persamaan?

Persamaan terutamanya datang daripada tiga idea klasik: 1) kejadian bersama temporal, 2) kejadian bersama spatial dan 3) jiran tempatan dalam kejiranan ruang isyarat asal) .

Apabila struktur asas ialah struktur geometri, idea-idea ini bertindih dengan ketara tetapi apabila struktur itu adalah struktur rawak, ia juga berbeza dari segi konsep, seperti yang ditunjukkan di bawah Menunjukkan perbezaan antara struktur manifold dan struktur kejadian bersama stokastik.

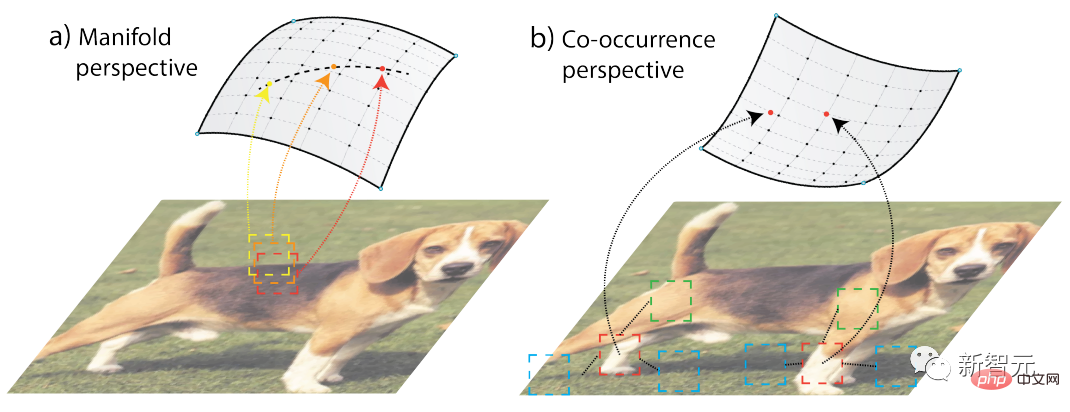
Menggunakan lokaliti, kerja berkaitan mencadangkan dua kaedah pembelajaran tanpa penyeliaan: pembelajaran manifold dan statistik kejadian bersama Pemodelan, kebanyakannya idea mencapai rumusan penguraian keturunan atau rumusan penguraian matriks yang berkait rapat.

Idea pembelajaran berlipat ganda ialah hanya kejiranan tempatan dalam ruang isyarat asal yang boleh dipercayai Dengan mempertimbangkan secara menyeluruh semua kejiranan tempatan, geometri global akan muncul, iaitu "Berfikir secara global , sesuai secara tempatan" (berfikir secara global, sesuai secara tempatan).

Sebaliknya, pemodelan statistik kejadian bersama mengikut falsafah kebarangkalian, kerana sesetengah struktur tidak boleh dimodelkan dengan manifold berterusan, jadi ia juga merupakan pelengkap kepada falsafah manifold.

Salah satu contoh yang paling jelas datangnya daripada bahasa semula jadi, di mana data asal pada asasnya tidak datang daripada geometri yang licin, seperti dalam pembenaman perkataan, pembenaman "Seattle" dan "Dallas " mungkin serupa, walaupun ia tidak berlaku bersama dengan kerap, sebab asasnya ialah ia mempunyai corak kontekstual yang serupa.

Perspektif kebarangkalian dan manifold saling melengkapi antara satu sama lain dalam memahami "kesamaan".

Bagaimana untuk mewujudkan transformasi perwakilan dalam artikel ini? Prinsip asas: sparsity dan pangkat rendah

Secara umum, sparsity boleh digunakan untuk mengendalikan lokaliti dan penguraian dalam ruang data untuk mewujudkan sokongan; Kemudian fungsi frekuensi rendah digunakan untuk membina transformasi perwakilan yang memberikan nilai yang serupa kepada titik yang serupa pada sokongan.

Keseluruhan proses juga boleh dipanggil transformasi manifold jarang.

Atas ialah kandungan terperinci Kemajuan terkini dalam model jarang! Ma Yi + LeCun bergabung tenaga: "Kotak putih" pembelajaran tanpa pengawasan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!