Ringkasan idea teknikal utama dan kaedah inferens sebab musabab

Pengenalan: Inferens sebab merupakan cabang penting sains data dan memainkan peranan penting dalam penilaian lelaran produk, algoritma dan strategi insentif dalam Internet dan industri . Walau bagaimanapun, inferens sebab-akibat bukanlah perkara yang mudah. Pertama, dalam kehidupan seharian, orang sering mengelirukan korelasi dengan sebab. Korelasi selalunya bermaksud bahawa dua pembolehubah mempunyai kecenderungan untuk meningkat atau menurun pada masa yang sama, tetapi sebab musabab bermaksud bahawa kita ingin tahu apa yang akan berlaku apabila kita menukar pembolehubah, atau kita menjangkakan untuk mendapatkan hasil kontrafaktual, jika kita melakukannya dalam masa lalu Jika kita mengambil tindakan yang berbeza, adakah akan ada perubahan pada masa hadapan? Kesukarannya, bagaimanapun, adalah bahawa data kontrafak selalunya sukar untuk diperhatikan dan dikumpulkan di dunia nyata.

Artikel ini ​ mengkaji dua sekolah inferens sebab - Model Rubin Causal (RCM; Rubin 1978) dan Model Causal Struktural Diagram Causal (Pearl 1995 )' idea dan kaedah teknikal utama, serta kaedah dan aplikasi baharu dalam beberapa tahun kebelakangan ini. Oleh kerana latar belakang akademik penulis secara relatifnya berkaitan dengan ekonometrik, kaedah dan makalah yang dipetik terutamanya merujuk kepada kesusasteraan ekonomi Mungkin terdapat beberapa kekurangan dalam kedalaman dan keluasan teori dan penggunaan beberapa kaedah.

Model hasil yang berpotensi

Kami menggunakan beberapa simbol dan formula matematik untuk menerangkan idea utama model hasil yang berpotensi. Pembaca juga boleh melangkau bahagian ini dan pergi terus ke kaedah tertentu.

Kami mewakili setiap objek penyelidikan atau pengguna dengan i, dan mereka mungkin tertakluk kepada campur tangan strategik tertentu: T_i=1 mewakili campur tangan (kumpulan eksperimen), T_i=0 tidak mewakili campur tangan (kumpulan garis dasar), dan hasil sepadan yang kami ambil berat ialah Y_i0 dan Y_i1, tetapi hanya satu keadaan yang akan berlaku, iaitu Y_i0 dan Y_i1Hanya satu daripadanya boleh diperhatikan, dan satu lagi tidak diketahui. Hasil inferens kausal yang kami jangkakan di sini ialah kesan rawatan purata ATE=E[Y₁-Y₀].

Kami boleh menerangkan kesukaran menganggar ATE melalui terbitan matematik tertentu. Memandangkan kita hanya akan memerhati satu daripada Y_i0 dan Y_i1 , apakah kita boleh mengira secara langsung sebenarnya perbezaan antara kumpulan E[Y_i1|T_i=1]-E[Y_i0|T_i =0], Perbezaan ini boleh dibongkarkan lagi kepada E[Y_i1|T_i=1]-E[Y_i0|T_i=1]+E[Y_i0| T_i=1]-E[Y_i0|T_i=0]. Di mana E[Y_i1|T_i=1]-E[ Y_i0|T_i=1] adalah pada individu dalam kumpulan eksperimen Kesan rawatan purata (ATT), ATT dan ATE selalunya tidak sama, dan perbezaan antara kedua-duanya mewakili kesahan luaran (External Validity) yang kami kira. Jika sampel dihadkan kepada pengguna kumpulan umur tertentu, keputusan mungkin tidak boleh digeneralisasikan kepada pengguna semua kumpulan umur, menunjukkan bahawa analisis kami mungkin tidak mempunyai kesahan luaran. Bahagian kedua formula di atas E[Y_i0|T_i =1]-E[Y_i0|T_i=0] Mewakili bias pemilihan sampel. Bias pemilihan mungkin selalunya tidak 0 dalam kehidupan sebenar Contohnya, jika kumpulan eksperimen dan kumpulan penanda aras tidak diambil secara rawak, dan akan terdapat perbezaan dalam taburan ciri tertentu, maka bias pemilihan mungkin berlaku. Oleh itu, perbezaan antara kumpulan yang kami kira sebenarnya mewakili kesan rawatan purata yang kami jangkakan hanya apabila bias pemilihan dihapuskan, mempunyai kesahan luaran dan berdasarkan sampel yang besar dan mencukupi. Kaedah pemikiran model kesan potensi sebenarnya adalah untuk mencapai keadaan sedemikian melalui tetapan dan model tertentu. Di sebalik ideanya, terdapat juga andaian matematik yang agak ketat. Di bawah, kami menyemak idea-idea utama dan pembangunan dan aplikasi teknologi dalam beberapa tahun kebelakangan ini mengikut kaedah yang berbeza Disebabkan oleh had ruang, kaedah regresi titik putus tidak akan diperkenalkan secara terperinci di sini.

1 Ujian A/B

Kaedah model kesan berpotensi yang paling biasa ialah percubaan rawak, atau ujian A/B yang biasa kami gunakan dalam industri. Kami membina kumpulan eksperimen dan kumpulan asas melalui persampelan rawak tertentu untuk memerhatikan perbezaan antara kumpulan. Walau bagaimanapun, perlu ditegaskan bahawa walaupun rambang dipenuhi, keberkesanan inferens sebab di sini masih perlu memenuhi andaian penting—Andaian Nilai Rawatan Unit Stabil (SUTVA). Potensi hasil setiap individu hanya relevan kepada dirinya sendiri dan tidak ada kaitan dengan sama ada individu lain diintervensi oleh strategi eksperimen Pada masa yang sama, intervensi strategik tunggal yang kita bimbangkan tidak mempunyai bentuk atau intensiti yang berbeza yang membawa kepada hasil potensi yang berbeza. Dalam kehidupan sebenar, terdapat banyak senario di mana andaian SUTVA dilanggar, yang juga telah memberi inspirasi kepada pembangunan pelbagai teknik ujian A/B baharu, seperti bajet atau kawalan strategik untuk masalah kesesakan, atau penambahbaikan dalam reka bentuk lencongan. Di sini kami memberikan beberapa contoh yang berkaitan dengan lencongan:

Di LinkedIn, penguji menggunakan kaedah percubaan pensampelan rangkaian untuk menangani cabaran yang ditimbulkan rangkaian sosial terhadap eksperimen rawak individu tradisional. Pertama, pengguna dibahagikan kepada kluster yang berbeza, dan setiap kluster digunakan sebagai individu untuk membahagi dan mengukur penunjuk eksperimen secara rawak Anggaran kesan rawatan diperbetulkan dengan menganggarkan pendedahan kesan rangkaian pengguna (Gui et al. 2015).

Pada platform seperti Airbnb, selalunya terdapat pengaruh bersama antara pembeli dan penjual, yang juga boleh mengganggu kaedah percubaan tradisional. Penyelidik membina penunjuk penilaian eksperimen melalui reka bentuk eksperimen dua hala dan model dinamik inventori (Johari et al. 2022). Perlu ditegaskan bahawa eksperimen dua hala adalah bidang yang agak baharu, dan reka bentuk percubaan mereka boleh membantu penguji menemui kesan limpahan eksperimen unilateral tradisional Walau bagaimanapun, sukar untuk membuat inferens statistik dan pembetulan pada keputusan eksperimen, dan mungkin tidak ada jawapan mutlak ia harus dibincangkan lebih dalam kombinasi dengan senario perniagaan.

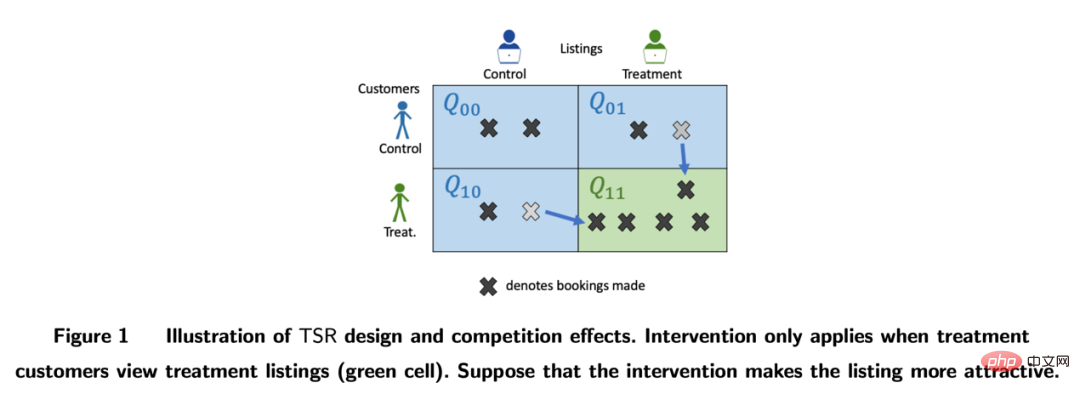
Imej daripada kertas Johari et al (2022)

2. Kaedah pembolehubah instrumental

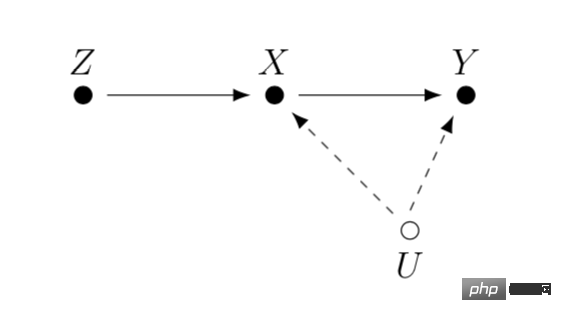
Pembolehubah instrumental ialah kaedah untuk menyelesaikan masalah endogeneiti regresi linear. Seterusnya, kami memperkenalkan masalah endogeneiti dan cara menyelesaikan endogeneiti melalui pembolehubah instrumental. Masalah utama dengan endogeneiti adalah jika kita mengambil berat tentang kesan X pada Y, tetapi terdapat pembolehubah U yang tidak diukur yang mempengaruhi kedua-dua X dan Y. Maka X adalah endogen, dan U ialah pembolehubah yang membingungkan yang disebutkan di atas. Jika kita boleh mencari pembolehubah Z yang berkaitan dengan X, dan Z tidak berkaitan dengan U. Kemudian kita boleh menggunakan Z sebagai pembolehubah instrumental untuk menganggar kesan sebab akibat X ke atas Y. Kaedah pengiraan khusus secara amnya ialah kaedah kuasa dua terkecil dua peringkat. Apabila kaedah pembolehubah instrumental sebenarnya digunakan, perhatian harus diberikan untuk mengelakkan masalah "pembolehubah instrumental yang lemah", iaitu korelasi antara pembolehubah instrumental Z dan pembolehubah minat X adalah sangat rendah, yang akan menyebabkan berat sebelah dalam anggaran kesan sebab Anda boleh bergantung pada kaedah ujian statistik untuk mengesahkan sama ada masalah sedemikian wujud.

Pembangunan kaedah pembolehubah instrumental adalah untuk menggabungkannya dengan model pembelajaran mendalam, contohnya, yang dicadangkan oleh Hartford et al (2017) Kaedah Deep IV. Penyelidikan ini mengubah kaedah kuasa dua terkecil dua peringkat tradisional bagi pembolehubah instrumental kepada tugas ramalan yang lebih fleksibel bagi dua rangkaian saraf dalam, melonggarkan andaian kukuh tentang proses penjanaan data (DGP) dalam kaedah tradisional.

Dalam aplikasi sebenar, berdasarkan senario yang terkumpul oleh sejumlah besar ujian A/B di Internet, kita boleh mempelajari penunjuk melalui pembelajaran meta eksperimen dan kaedah pembolehubah instrumental hubungan sebab akibat antara. Sebagai contoh, Peysakhovich & Eckles (2018) menggunakan data Facebook, menggunakan maklumat kumpulan eksperimen sebagai pembolehubah instrumental, dan menggabungkan penyelarasan L0 berdasarkan kaedah kuasa dua terkecil dua peringkat, yang boleh menyelesaikan masalah bias pembolehubah instrumental tradisional kaedah pada sampel terhad, dan juga boleh Mengatasi masalah nilai mutlak kesan yang agak rendah ("pembolehubah instrumental lemah") diperhatikan dalam sebilangan besar eksperimen dalam situasi dunia sebenar.

Selain mempelajari hubungan pengaruh antara penunjuk, idea pembolehubah instrumental juga boleh digunakan untuk menyelesaikan masalah berat sebelah dalam sistem pengesyoran. Dalam sistem pengesyoran, latihan model sering bergantung pada pandangan sejarah pengguna dan gelagat maklum balas suka, tetapi data sejarah ini sering dipengaruhi oleh faktor yang mengelirukan seperti lokasi paparan dan mod pendedahan. mencadangkan rangka kerja IV4Rec menggunakan idea pembolehubah instrumental, menggunakan pertanyaan carian sebagai pembolehubah instrumental untuk menguraikan hubungan sebab dan bukan sebab dalam pembenaman sistem pengesyoran Digabungkan dengan pembelajaran mendalam, ia boleh digunakan pada kedua-dua data Kuaishou dan set data awam MINDA Sahkan kesan penambahbaikan model pengesyoran.

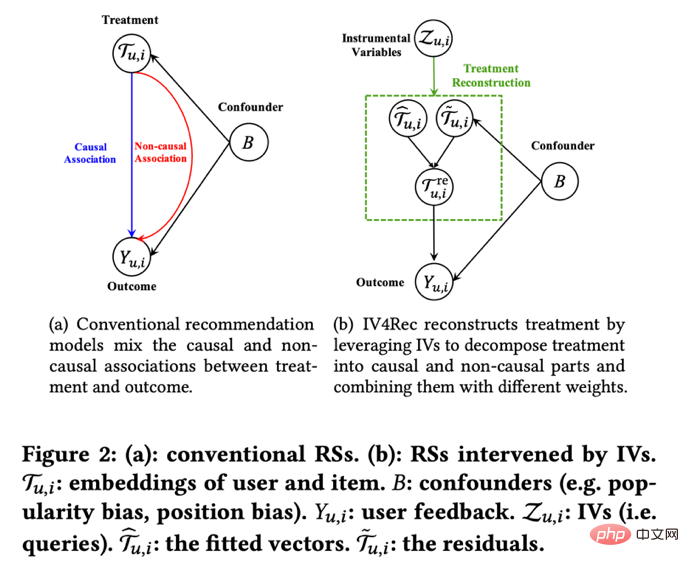
Imej daripada kertas Si et al (2022)

3. Kaedah pemadanan

Pemadanan ialah kaedah analisis sebab yang digunakan secara meluas oleh perniagaan, terutamanya untuk Untuk menyelesaikan masalah apabila kumpulan eksperimen dan kumpulan kawalan adalah tiada tandingan atas sebab tertentu (confounder), setiap pengguna dalam kumpulan eksperimen dipadankan dengan pengguna yang paling serupa dengannya dalam ciri-ciri tertentu (padanan berbutir kasar CEM) atau kebarangkalian untuk menerima intervensi (kecenderungan skor) ) pengguna kumpulan kawalan (padanan skor kecenderungan PSM) yang paling serupa, dan cipta semula kumpulan eksperimen dan kawalan yang setanding. Pemadanan ialah kaedah yang paling serupa dengan eksperimen rawak AB/RCT (percubaan terkawal rawak) Kaedah operasi adalah agak serupa, dan hasilnya sangat intuitif. Tambahan pula, pemadanan ialah kaedah bukan parametrik untuk menganggar kesan rawatan dan tidak tertakluk kepada andaian umum model parametrik linear. Dengan memadankan sampel, kaedah perbezaan berganda juga boleh digunakan, yang sering digunakan untuk menyelesaikan masalah kadar penembusan rendah fungsi baru. Dalam tahun-tahun kebelakangan ini, pembangunan kaedah pemadanan terutamanya telah digabungkan dengan model pembelajaran mesin untuk menjadikan pemadanan skor kecenderungan lebih tepat Pada masa yang sama, idea-idea di sini juga telah digunakan pada beberapa kaedah penyebab lain dan pembetulan model pembelajaran mesin kandungan akan dibincangkan kemudian.

4 Siri kaedah dan perkembangan dalam data panel

Dalam beberapa tahun kebelakangan ini. , sekitar Terdapat banyak kaedah baharu untuk inferens sebab bagi data panel. Mari kita semak dahulu kaedah data panel tradisional.

Kaedah yang paling biasa digunakan ialah kaedah perbezaan berganda. Perbezaan dalam perbezaan yang paling mudah ialah mengawal perbezaan antara kumpulan dan menggunakan bentuk model regresi untuk menerangkan y_ia=α₀+α ₁ Layan_i+α₂Catatan_t+α₃Layan_i* Siarkan_t. Here Treat_i=1 mewakili sama ada individu tersebut telah campur tangan, Post_t= 1 mewakili tempoh masa pemerhatian selepas intervensi. Melalui jadual di bawah, kita dapati bahawa α₂+α₃ ialah percubaan Nilai perbezaan kumpulan sebelum dan selepas tarikh percubaan, α₂ ialah nilai perbezaan kumpulan kawalan sebelum dan selepas tarikh percubaan . Perbezaan antara dua item ini, α₃ ialah anggaran kesan sebab, yang juga merupakan pekali bagi istilah interaksi dalam model di atas, dan ialah hasil daripada dua perbezaan .

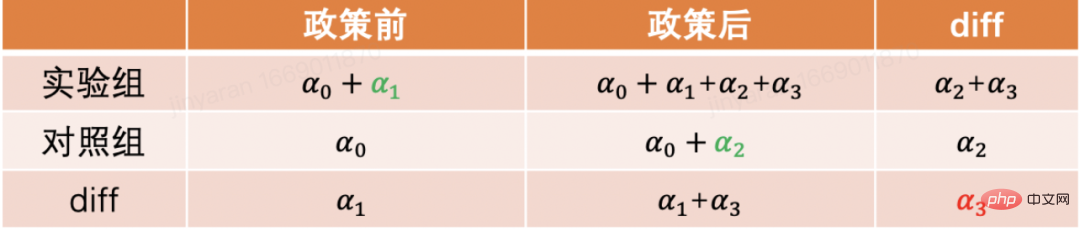
Kaedah perbezaan dalam perbezaan bergantung pada andaian yang lebih ketat. "Aliran selari" ialah premis yang paling penting, iaitu nilai min penunjuk hasil kumpulan eksperimen dan kumpulan penanda aras sebelum campur tangan dasar adalah stabil dari semasa ke semasa Ini menunjukkan bahawa kesan faktor lain kecuali dasar intervensi itu sendiri adalah sama untuk kumpulan eksperimen dan kumpulan penanda aras. Kita boleh menggunakan plot arah aliran masa untuk menguji hipotesis selari, dan beberapa pakej inferens statistik juga menyediakan fungsi yang sepadan. Apabila ujian selari gagal, ujian lanjut boleh dilakukan dengan menambahkan pembolehubah kawalan atau istilah arah aliran masa pada regresi. Dalam sesetengah kes, ia juga boleh diselesaikan dengan bantuan kaedah perbezaan tiga kali ganda. Di samping itu, dalam amalan sebenar, terdapat banyak cara untuk melaksanakan kaedah perbezaan berganda. Sebagai tambahan kepada kaedah yang dinyatakan di atas, tetapan "model kesan tetap dua hala" juga boleh diguna pakai Y_it=τTreat_it+X_ia β+α_i+ξ_t+ε_ia, tetapi juga bergantung pada andaian yang kukuh: ada tiada perubahan dari semasa ke semasa faktor yang mengelirukan, dan keputusan lepas tidak akan menjejaskan status rawatan semasa, dan ia juga memerlukan kesan rawatan dasar kekal tidak berubah. Berkenaan dengan batasan teori dan kaedah di belakangnya, serta kaedah baharu yang diperluaskan seperti pemadanan dan pemberatan semula, adalah disyorkan untuk belajar dalam kombinasi dengan kursus yang diajar oleh Profesor Xu Yiqing dari Universiti Stanford:

​https://yiqingxu.org/teaching/​

Di sini kami menyenaraikan beberapa yang lebih biasa digunakan kaedah baharu:

Kaedah kawalan sintetik ialah satu set kaedah yang diperoleh daripada kaedah inferens sebab-akibat data panel, dan penyelidikan ujian anggaran atau inferens statistik sentiasa muncul. Apabila intervensi dilaksanakan dalam kumpulan atau wilayah, kumpulan eksperimen hanya mempunyai satu nilai pemerhatian pada satu titik masa, dan tempoh masa data adalah panjang, seperti bandar melakukan aktiviti promosi tempatan, biasanya perbezaan dalam- kaedah perbezaan tidak sesuai Pada masa ini, kaedah kawalan sintetik boleh diguna pakai. Prinsipnya adalah untuk memilih beberapa bandar kawalan dan memasukkannya ke dalam "kumpulan kawalan maya" yang hampir sama dengan kumpulan eksperimen sebelum campur tangan Untuk pengenalan dan pengoptimuman teori terperinci dalam beberapa tahun kebelakangan ini, sila rujuk Profesor Aberto Abadie dari Massachusetts Institute. of Technology dan rakan kerjasamanya (Abadie, Diamond and Hainmueller 2010) dan kursus pendeknya di NBER untuk pengajian lanjut:

​https://www. nber.org/ lecture/2021-summer-institute-methods-lecture-alberto-abadie-synthetic-controls-methods-and-practice​

Perbezaan berganda kaedah dan kawalan sintetik Malah, semua undang-undang boleh disatukan dalam satu set sistem rangka kerja analisis. Penyelidikan oleh Arkhangelsky et al (2021) menunjukkan bahawa perbezaan dalam perbezaan menyelesaikan masalah regresi kesan tetap dua hala tanpa sebarang pemberat individu atau masa, manakala kaedah kawalan sintetik menggunakan pemberat ω kepada individu sebelum campur tangan polisi berlaku agar sesuai. campur tangan individu, makalah ini menggabungkan dua kaedah untuk mencadangkan penganggar baharu: perbezaan berganda sintetik (SDID), yang merangkumi kedua-dua berat individu ω dan berat masa λ, dengan itu meningkatkan kekukuhan penganggar keseluruhan. Berat masa λ di sini boleh difahami sebagai tempoh data yang lebih serupa dengan tempoh selepas intervensi diberi pemberat yang lebih tinggi.

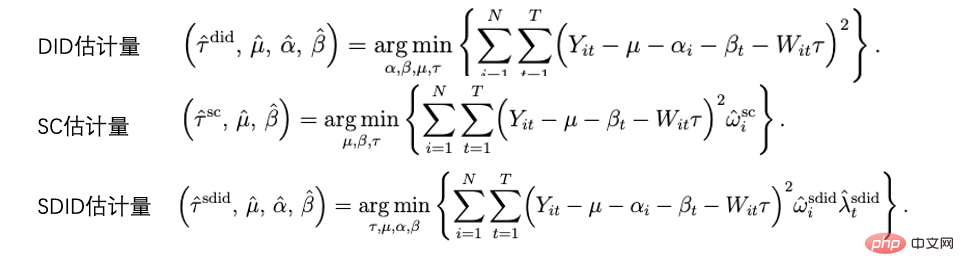
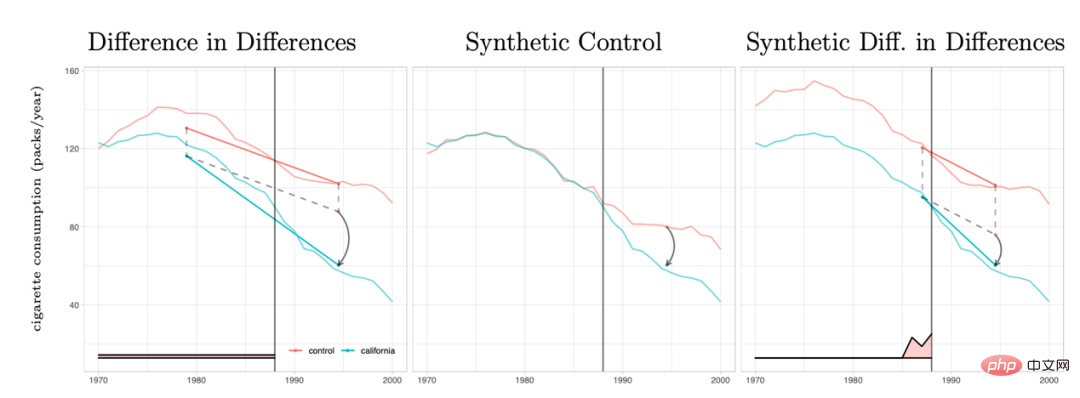
Perbandingan beberapa kaedah: Gambar daripada karya Arkhangelsky et al. 2021)

Data panel juga boleh digabungkan dengan kaedah penyiapan matriks untuk inferens sebab, yang juga merupakan perkembangan baharu dalam bidang ini sejak beberapa tahun kebelakangan ini. Algoritma penyiapan matriks menyelesaikan masalah kehilangan data kontrafaktual yang dihadapi oleh inferens sebab dengan menyelesaikan masalah pengoptimuman cembung. Kaedah ini sesuai untuk situasi di mana individu tertakluk kepada masa campur tangan dasar yang tidak konsisten Contohnya, lelaran produk memerlukan pengguna mengemas kini versi produk untuk berkuat kuasa, tetapi masa kemas kini pengguna tidak konsisten. Untuk teori kaedah terperinci, sila rujuk kertas berkaitan seperti Athey et al (2021). Kaedah penyiapan matriks, kawalan sintetik dan kaedah ramalan regresi di bawah campur tangan rawak juga boleh disatukan di bawah rangka kerja masalah pengoptimuman, dan kami juga boleh menggabungkan pelbagai kaedah dalam cara ensemble untuk mendapatkan hasil anggaran yang lebih mantap (Athey et.al 2019).

Rajah penyiapan matriks: Gambar datang dari kursus Guidon Imbens di AEA, di mana W mewakili status rawatan https: //www.aeaweb.org/conference/cont-ed/2018-webcasts

Di atas dalam bahagian ini kami memperkenalkan kaedah utama data panel inferens sebab dan Kemajuan, bidang ini adalah bidang dengan kaedah yang sangat pelbagai dan kemajuan yang sangat pantas Walau bagaimanapun, pengguna perlu mempertimbangkan sepenuhnya andaian dan batasan di sebalik kaedah untuk menilai dengan lebih tepat pelbagai dasar dalam amalan. Di sini kami hanya memberikan pengenalan yang sangat ringkas.

5 Semakan kaedah untuk kesan penyebab heterogen

Digabungkan dengan pembelajaran mesin. kaedah Mengkaji kesan sebab akibat heterogen sebenarnya merupakan satu trend dalam perkembangan inferens sebab akibat dalam beberapa tahun kebelakangan ini. Mari kita perkenalkan dahulu kesan sebab akibat heterogen: Kesan Rawatan Heterogen (HTE) merujuk kepada fenomena bahawa eksperimen menghasilkan kesan berbeza ke atas individu disebabkan ciri individu sampel yang berbeza. Dinyatakan dalam kombinasi dengan formula matematik, HTE mempunyai banyak bentuk:

Kesan penyebab setiap individu ITE (kesan rawatan individu): τ_i=Y_i1-Y_i0, Y Hanya satu daripada _i1 dan Y_i0 boleh diperhatikan, dan satu lagi dan τ_i perlu dianggarkan melalui kaedah model tertentu.

Purata kesan penyebab kumpulan pada ciri-ciri tertentu Di sini kita menggunakan X untuk mewakili ciri, maka anggaran CATE (kesan rawatan purata bersyarat) adalah terhad Purata kesan kausal pada populasi dengan nilai khusus tertentu bagi ciri: τ(x)=E[Y₁-Y₀|X=x].

Kaedah analisis HTE pada masa ini mempunyai pelbagai senario aplikasi. Melalui HTE, kita boleh mengetahui ciri-ciri kumpulan yang paling bertindak balas terhadap campur tangan strategik tertentu Ia juga boleh membantu kita menyiasat mekanisme strategi ujian A/B yang mempunyai kesan yang dijangka atau tidak mempunyai kesan digunakan untuk pelbagai pemperibadian antara strategi. Kaedah inferens sebab heterogen mempunyai banyak aplikasi dalam industri dan Internet Sebagai contoh, ia digunakan dalam TripAdvisor untuk mengukur insentif pendaftaran ahli Di Microsoft, kaedah ini dan data jangka pendek digunakan untuk mengukur ROI jangka panjang projek yang berbeza kes permohonan terperinci boleh didapati Rujuk kursus latihan KDD 2021 (https://causal-machine-learning.github.io/kdd2021-tutorial/).

Kaedah yang paling biasa untuk kesan penyebab heterogen sebenarnya adalah analisis multidimensi yang biasa digunakan dalam analisis eksperimen Walau bagaimanapun, penggunaan analisis multidimensi memerlukan kewaspadaan terhadap masalah berbilang ujian. Pada masa yang sama, apabila terdapat dimensi yang mencukupi, terdapat keperluan yang agak tinggi untuk saiz sampel eksperimen, dan kecekapan analisis agak rendah. Kaedah pembelajaran mesin menyediakan beberapa kaedah perlombongan yang meningkatkan kecekapan Kelebihannya ialah ia secara adaptif dapat mempelajari pengedaran kesan sebab-akibat heterogen dan tidak memerlukan andaian bentuk fungsional yang ketat Ia lebih baik daripada kaedah ekonometrik tradisional berdasarkan regresi linear kaedah mempunyai darjah kebebasan yang lebih kuat, tetapi cabaran teknikal ialah bagaimana membuat inferens statistik. Dalam tahun-tahun kebelakangan ini, dengan pendalaman gabungan pembelajaran mesin dan ekonometrik, banyak set kaedah telah diinovasikan dan digunakan dalam bidang ini Di sini kita memberi tumpuan kepada jenis kaedah berikut. Andaian asas kaedah ini adalah andaian kebebasan bersyarat (. Conditional Independence Assumption), iaitu, hanya apabila pelbagai pembolehubah yang mengelirukan dikawal dengan secukupnya, kita boleh mendapatkan anggaran kesan sebab akibat yang agak tepat.

Hutan sebab: Berdasarkan hutan rawak, ia merupakan kaedah bukan parametrik yang secara langsung melaksanakan anggaran yang sesuai. Logik anggaran utama pokok penyebab adalah untuk menentukan fungsi kehilangan pokok keseluruhan dengan mentakrifkan kesan sebab pada setiap daun. Pokok penyebab bertujuan untuk memaksimumkan jumlah kehilangan semua daun mengikut cara tertentu untuk membelah X. Selain matlamat anggaran yang berbeza daripada algoritma pokok dalam pembelajaran mesin, perbezaan lain ialah dalam algoritma inferens sebab, sampel set latihan biasanya dibahagikan kepada set latihan dan set anggaran Set latihan digunakan untuk pembahagian daun, dan set anggaran digunakan Kira purata kesan rawatan pada setiap nod daun selepas berdaun. Kelebihan pokok penyebab ialah hasilnya sangat ringkas dan mudah difahami Anda boleh mengenal pasti secara langsung kumpulan orang mana yang mempunyai perbezaan yang jelas dalam kesan eksperimen melalui timba Penunjuk timba yang pertama selalunya merupakan dimensi terbesar perbezaan kesan sebab . Walau bagaimanapun, pokok penyebab terdedah kepada overfitting Dalam kerja amali, adalah disyorkan untuk menggunakan hutan rawak sebab (untuk butiran, sila rujuk Athey dan Imbens 2016, Wager dan Athey 2018 Pada masa yang sama, hutan rawak sebab-sebab juga mempunyai lebih baik). sifat inferens statistik. Untuk pengembangan kaedah ini, sila rujuk kerja penyelidikan seperti Athey, Tibshirani and Wager (2019) dan Friedberg et al (2020) Kaedah baharu ini boleh menangani masalah apabila terdapat pembolehubah yang mengelirukan dan menganggarkan hasilnya dengan lebih lancar .

Pelajar Meta: Berbeza daripada model yang menggunakan pokok sebab untuk menganggarkan secara langsung kesan sebab, ia adalah sejenis model anggaran tidak langsung: melalui Model pembolehubah hasil Y secara langsung. Oleh itu, Meta Learner tidak boleh terus menggunakan anggaran HTE untuk inferens statistik Dalam aplikasi sebenar, sesetengah penyelidik akan menggunakan bootstrap untuk menyelesaikan masalah ini. Terdapat tiga jenis algoritma anggaran Meta Learners: T-Learner, S-Learner dan X-Learner. Perbezaan asas antara tiga kaedah ialah:

Yang paling mudah ialah S-learner. Ia menggunakan pembolehubah pencelah sebagai pembolehubah ciri untuk pemodelan satu masa, yang sesuai untuk digunakan dalam situasi di mana pembolehubah rawatan dan hasil berkorelasi kuat, jika tidak model tidak dapat mengenal pasti perubahan dalam hasil yang disebabkan oleh perubahan dalam pembolehubah pencelah

Yang lebih rumit sedikit ialah T-learner. Ia mengenal pasti kesan sebab dengan memaksa dua model mempelajari Y_i1 kumpulan eksperimen dan Y_i0 masing-masing. Ia sesuai digunakan apabila terdapat banyak pembolehubah dalam eksperimen kumpulan dan kumpulan kawalan dan lebih purata, jika tidak, salah satu model akan lebih teratur; jumlah data adalah kecil (lihat Künzel et al. 2019 untuk butiran lanjut).

Rangka kerja anggaran berdasarkan DML dan DRL: Kami memperkenalkan kedua-dua rangka kerja ini bersama-sama dengan alat Econml Microsoft:

​https://www.microsoft.com/en-us/research/project/econml/​

DML (pembelajaran mesin berganda) ialah kaedah rangka kerja untuk pembolehubah mengelirukan secara fleksibel dan hubungan antara pembolehubah pemprosesan dan pembolehubah hasil dengan kehadiran pembolehubah pengeliru berdimensi tinggi Seperti namanya, kaedah ini digunakan dalam anggaran Kesan penyebabnya ialah terutamanya dibahagikan kepada dua langkah: langkah pertama ialah menggunakan dua (tidak semestinya sama) model pembelajaran mesin untuk menganggarkan dua jangkaan bersyarat E(Y|X,W) dan E(T|X,W) masing-masing, dan kemudian Ambil baki. Di sini kedua-dua X dan W adalah pembolehubah yang mengelirukan, tetapi hanya X ialah pembolehubah yang berkaitan dalam CATE. Langkah kedua ialah menganggarkan ATE atau CATE berdasarkan baki Apabila menganggar CATE, baki T-E(T|X,W) didarab dengan fungsi θ(X) kira-kira X untuk anggaran. Untuk maklumat tentang cara menganggarkan ATE, sila rujuk Chernozhukov et al (2018). Econml menyediakan banyak model untuk dipilih dalam langkah kedua: LinearDML (menggunakan model OLS), DML (menggunakan model tersuai), CausalForestDML (menggunakan hutan rawak penyebab)... Apabila menggunakan rangka kerja DML, anda perlu memberi perhatian untuk menyemak sama ada cara istilah baki kedua-dua model adalah berbeza dengan ketara daripada 0 atau berkorelasi dengan ketara. Jika ya, ini bermakna pembolehubah yang mengelirukan mungkin tidak cukup dikawal.

Rangka kerja DRL adalah berdasarkan kaedah Doubly Robust, yang juga dibahagikan kepada dua langkah Langkah pertama menggunakan X, W, T untuk meramalkan Y, dan mentakrifkan nilai ramalan sebagai g

t

(X,W); dalam langkah kedua, model pengelasan digunakan untuk meramalkan T menggunakan X, W hingga dapatkan skor kecenderungan, yang ditakrifkan sebagai p_t(X,W). Perlu diingat bahawa T di sini ialah pembolehubah diskret, dan ia terhad kepada g_t(X,W) beberapa jenis model berasaskan regresi. Selepas keputusan dua langkah, pembolehubah hasil terlaras dikira:

Kemudian Y terlaras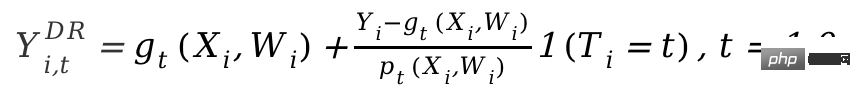

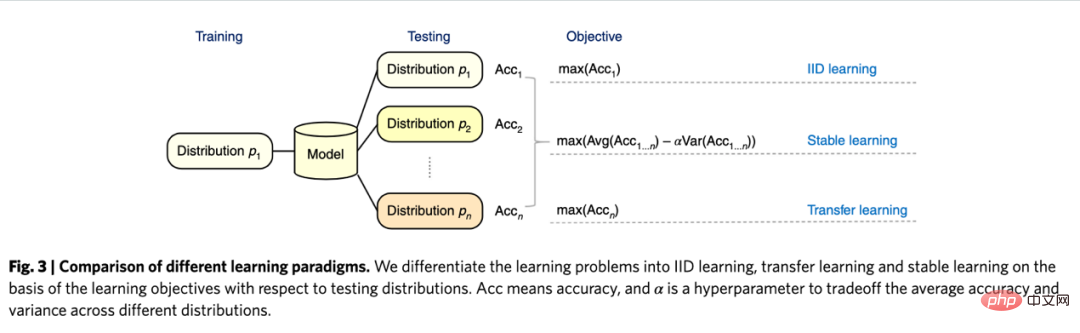
i,tDRCari perbezaan Y antara kumpulan eksperimen dan kumpulan kawalan i1DR-Yi0DR, kembalikan X untuk dapatkan CATE. Sebab mengapa DRL dipanggil Doubly Robust ialah dalam formula di atas, gt(X,W) dan p_{t Selagi satu anggaran dalam} (X, W) adalah betul, anggaran kesan sebab adalah tidak berat sebelah. Tetapi jika kedua-dua anggaran model salah, ralat yang terhasil boleh menjadi sangat besar. Sama seperti DML, perbezaan antara pelbagai Pelajar DRL dalam Econml ialah jenis model yang digunakan untuk menyesuaikan Y dengan X >-Y i0_DR .

Cabaran aplikasi terbesar kaedah inferens sebab heterogen berdasarkan model pembelajaran mesin sebenarnya ialah cara memilih model pembelajaran mesin yang sesuai dan melaraskan parameter untuk mendapatkan hasil anggaran yang agak mantap. Berdasarkan pengalaman permohonan dan penyelidikan terkini, terdapat langkah berjaga-jaga berikut:

• Pastikan saiz sampel latihan cukup besar.
• Jika anda menggunakan alat Econml, adalah disyorkan untuk menggunakan fungsi skor* untuk memilih model (skor yang lebih kecil, model yang lebih baik), tetapi tidak setiap model mempunyai fungsi ini: seperti Terdapat DML tetapi bukan X-Learner atau Causal Forest. Jika anda menggunakan Uber's Causalml, anda boleh menggunakan carta Kumulatif Keuntungan untuk membandingkan prestasi pelbagai Meta Learners.
  https://github.com/uber/causalml​.
• Sesetengah kaedah boleh melakukan ujian statistik pada HTE, tetapi yang lain tidak boleh. Dalam Econml, kaedah yang boleh digunakan untuk melaksanakan ujian statistik pada HTE adalah terhad kepada kaedah menetapkan model langkah terakhir dalam DML/DRL kepada model linear atau hutan sebab, manakala pembolehubah ciri X dan pembolehubah eksperimen T adalah tidak linear berkaitan dalam banyak senario perniagaan. Memaksa model linear boleh menyebabkan bias anggaran HTE (contohnya, turun naik HTE tiada kaitan dengan X dan hanya bunyi bising). Jika individu yang mempunyai HTE yang ketara akan disaring untuk analisis seterusnya, pembetulan ujian berbilang untuk ujian kesan individu diperlukan.
• Selain darjah pemasangan model, standard juga diperlukan untuk mengukur kualiti anggaran HTE: contohnya, sama ada julat perubahan HTE adalah besar cukup untuk membezakan kumpulan sensitif daripada kumpulan tidak sensitif , anda boleh merujuk kepada inferens statistik berdasarkan ciri HTE yang dicadangkan oleh Chernozhukov et al (2018), yang juga sangat mudah digunakan.

Kaedah yang diperkenalkan di atas pada asasnya memfokuskan pada kesan sebab akibat heterogen statik di bawah pembolehubah selang. Tetapi dalam aplikasi praktikal, masalah yang akan kita hadapi akan menjadi lebih kompleks. Contohnya, berbilang pembolehubah campur tangan terlibat: insentif subsidi yang diberikan oleh produk kepada pengguna mungkin termasuk kedua-dua insentif log masuk dan ganjaran untuk tugasan lain Cara mengimbangi pengagihan pelbagai jenis insentif boleh ditakrifkan sebagai pembinaan kesan sebab-akibat yang heterogen daripada pelbagai pembolehubah campur tangan pemodelan dan masalah pengoptimuman. Contoh lain ialah kesan penyebab dinamik, di mana pembolehubah yang mengelirukan berubah dengan campur tangan pada masa yang berbeza (lihat Lewis dan Syrgkanis 2020). Mari kita ambil tugas insentif sebagai contoh Tugasan ini mungkin menyebabkan pengguna memberi perhatian kepada sauh baharu, dengan itu mengubah pilihan mereka untuk melihat kandungan, dan juga akan menjejaskan kesan insentif berikutnya. Senario yang kompleks ini telah memberi inspirasi kepada pengembangan selanjutnya pelbagai kaedah, dan kami juga mengharapkan penyelidikan dan aplikasi yang lebih mantap dan sistematik yang muncul pada masa hadapan.

Model Kausalitas Struktur

Dalam bahagian sebelumnya kami memperkenalkan idea utama dan pembangunan metodologi model hasil terpendam. Kaedah sekolah jenis ini mempunyai teori statistik yang agak lengkap dan boleh memperoleh keputusan anggaran yang agak tepat. Walau bagaimanapun, terdapat had tertentu Ia hanya boleh digunakan untuk menganggarkan pengaruh satu darjah korelasi antara pembolehubah (iaitu, hanya satu pembolehubah bersandar dan beberapa pembolehubah bebas dibenarkan, dan pautan kesan tidak langsung tidak boleh dianggarkan). antara banyak pembolehubah Pautan dan perhubungan yang kompleks memerlukan penggunaan kaedah model penyebab struktur sekolah lain.

Model penyebab berstruktur menggunakan graf asiklik terarah (DAG) untuk menerangkan hubungan sebab akibat dan taburan bersyarat antara pembolehubah. Setiap nod graf ialah pembolehubah dan hubungan sebab akibat diwakili oleh tepi yang menghubungkan nod ini, contohnya, 2 mewakili X2 menjejaskan >, kami juga memanggil X₁ sebagai nod anak, 🎜> ialah nod induk. Untuk set pembolehubah rawak X=(X1, ..., DAG yang dibentuk oleh >p_j=1P(X_j|pa _j), di mana pa_j ialah X_jnod induk segera . Apabila kami menyatakan kausaliti, kami memperkenalkan konsep pengendali lakukan, dengan mengandaikan bahawa X=(X¹, 🎜>2 ,... ,x2,...xp), gunakan do( >) bermaksud campur tangan untuk pembolehubah Xj (tugaskan kepada 🎜>) , maka kita boleh mendapatkan DAG baharu berdasarkan hubungan taburan bersyarat antara pembolehubah: P(X1=x 1, 🎜>,..., >|do( Perubahan jangkaan antara satu sama lain di bawah taburan lama ialah kesan sebab akibat 1|do)(Xj=x'j )-E (X1|do(Xj =xj)). Judea Pearl, pengasas model kausal hasil, menegaskan dalam penyelidikannya bahawa apabila menggunakan rajah kausal untuk mengenal pasti hubungan kausal, jika "kriteria pintu belakang" dan "kriteria pintu depan" dipenuhi, sebenarnya tidak perlu untuk memerhatikan semua pembolehubah. Mengenai khusus Sila rujuk Pearl (2009) untuk butiran teori. Perlu ditambah bahawa model penyebab struktur dan model hasil potensi sebenarnya adalah berkaitan.

Dalam aplikasi praktikal, kita mungkin tidak mempunyai maklumat secara langsung untuk mentakrifkan graf sebab, jadi cara untuk mempelajari struktur graf sebab antara pembolehubah telah menjadi isu penting. Apabila menyelesaikan jenis masalah ini, mula-mula kita perlu menjelaskan andaian yang diperlukan:

Causal Markov Causal Markov hypothesis: Andaian ini bermaksud bahawa pengagihan bersyarat mana-mana nod hanya berdasarkan nod induk terdekatnya.

Andaian Kecukupan Sebab: Andaian ini bersamaan dengan ketiadaan pembolehubah mengelirukan yang tidak boleh diperhatikan.

Kesetiaan Sebab-sebab Andaian Kesetiaan Sebab: Andaian ini bermakna berdasarkan beberapa taburan kebarangkalian bersyarat, beberapa nod adalah bebas antara satu sama lain (jadi graf boleh dipotong).

Algoritma secara kasar dibahagikan kepada dua kategori:

Untuk pengenalan terperinci, sila rujuk Glymour, Zhang and Sprites (2019) dan artikel "Statistical Methods for Causal Inference" dalam isu ke-12 "Science China: Mathematics" pada 2018:

https://cosx.org/2022/10/causality-statistical-method/​.

Algoritma berasaskan kekangan: Berdasarkan ujian bebas pengagihan bersyarat, pelajari semua yang memenuhi kesetiaan dan andaian markov kausal Gambar rajah kausal, iaitu menguji sama ada taburan bersyarat antara dua nod adalah bebas. Sebagai contoh, algoritma PC (Spirtes dan Glymour 1991) dan algoritma IC (Verma dan Pearl 1990).

Algoritma berasaskan skor: Cari padanan terbaik untuk data dengan mengoptimumkan struktur graf yang ditentukan skor tertentu . Persamaan struktur dan fungsi skor perlu ditakrifkan. Sebagai contoh, algoritma CGNN (Goudet et al. 2017) dan algoritma NOTEARS (Zheng et al. 2018). Di sini kita fokus pada algoritma NOTEARS. Algoritma tradisional adalah berdasarkan semua nod dan kemungkinan hubungan antara nod, mencari dalam semua graf yang mungkin, dan memilih penyelesaian optimum mengikut piawaian tertentu Ini adalah masalah NP-hard biasa dan menggunakan Ia mengambil masa yang sangat lama dan pengkomputeran semasa sumber pada asasnya tidak dapat memenuhi keperluan pengkomputeran. Algoritma NOTEARS mengubah masalah carian diskret kepada masalah carian berterusan. Algoritma ini sangat meningkatkan kelajuan pengkomputeran dan menjadikannya boleh digunakan oleh penganalisis data biasa. Walau bagaimanapun, kaedah ini juga mempunyai had tertentu Sebagai contoh, diandaikan bahawa bunyi semua pembolehubah mesti diedarkan Gaussian Dalam beberapa tahun kebelakangan ini, semakin banyak kaedah (seperti He et al. 2021) telah cuba menambah baik andaian. kaedah sedemikian.

Dengan perkembangan bidang pembelajaran peneguhan, kami juga mendapati bahawa inferens sebab dan pembelajaran peneguhan boleh digabungkan antara satu sama lain untuk menggalakkan perkembangan satu sama lain. Inferens sebab boleh membantu algoritma pembelajaran pengukuhan mempelajari fungsi nilai atau strategi optimum dengan lebih cekap dengan membuat kesimpulan hubungan sebab akibat antara keadaan atau antara keadaan dan tindakan dalam pembelajaran pengukuhan. Pembaca yang berminat dalam aspek ini boleh merujuk kepada Profesor Elias Bareinboim dari Columbia University. ​​https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d​​ Sebaliknya, pembelajaran peneguhan juga boleh disepadukan ke dalam algoritma pembelajaran graf sebab, seperti Zhu, Ng, dan Chen (2019) di Makmal Bahtera Nuh Huawei.

Mengenai prospek masa depan inferens sebab, kita harus menyebut paradigma penyelidikan baharu yang berkaitan dengan pembelajaran graf, inferens sebab dan pembelajaran mesin dalam beberapa tahun kebelakangan ini, iaitu "pembelajaran stabil" yang dicadangkan oleh pasukan Profesor Cui Peng dari konsep Universiti Tsinghua (Cui dan Athey 2022). Aplikasi model seperti pembelajaran mesin dan kecerdasan buatan bergantung pada andaian penting - andaian Bebas dan Teragih Identik. Maksudnya, set latihan dan set ujian perlu datang dari pengedaran yang sama, tetapi sebenarnya terdapat pelbagai masalah OOD (Out Of Distribution, out of distribution) Pada masa ini, prestasi model tidak dapat dijamin Ini juga merupakan masalah yang dihadapi oleh pelbagai model dalam sejarah. Inferens sebab boleh membantu mengatasi masalah tersebut. Sekiranya struktur boleh dijamin mempunyai kesan ramalan yang sama dalam pelbagai persekitaran untuk mengatasi masalah OOD, maka struktur ini mestilah struktur penyebab, dan prestasi struktur sebab dalam pelbagai persekitaran adalah agak stabil. Penyelidikan oleh pasukan Cui Peng (He et al. 2022, Shen et al. 2021) mendapati bahawa dengan menggunakan idea mengelirukan keseimbangan padanan pembolehubah, semua pembolehubah boleh dibuat bebas dengan menimbang semula sampel, menjadikan model berasaskan korelasi Menjadi Become model berasaskan sebab-akibat. Apa yang dipanggil pembelajaran stabil adalah menggunakan set latihan satu pengedaran dan satu set ujian pelbagai taburan yang tidak diketahui Matlamat pengoptimuman adalah untuk meminimumkan varians ketepatan. Saya percaya ini adalah bidang yang sangat penting pada masa hadapan, dan pembaca yang berminat boleh terus memberi perhatian kepada kemajuan penyelidikan yang berkaitan.

Perbandingan pembelajaran bebas dan teragih sama, pembelajaran pemindahan dan pembelajaran stabil: Gambar dari kertas Cui dan Athey 2022

Dalam aplikasi praktikal, pembelajaran mesin dan bidang berkaitan kecerdasan buatan seperti sistem pengesyoran, penglihatan komputer, pemanduan autonomi, pemprosesan bahasa semula jadi, dll. penuh dengan inferens sebab dan pembelajaran graf sebab telah menggalakkan pembangunan bidang ini. dan Universiti Oxford (Kaddour et al. 2022). Dalam bidang sistem pengesyoran, seperti yang kami perkenalkan dalam aplikasi kaedah pembolehubah instrumental, sistem pengesyoran tidak dapat dielakkan mempunyai berat sebelah Mengenal pasti hubungan graf sebab antara pengguna dan item boleh membantu sistem pengesyoran membetulkan bias. Sebagai contoh, Wang et al (2021) dan Zhang et al (2021) masing-masing menggunakan rajah sebab untuk menghapuskan bias yang disebabkan oleh clickbait. Dalam bidang pemanduan autonomi, penyelidik dari Microsoft melancarkan CausalCity (McDuff et al. 2022), platform persekitaran pemanduan simulasi yang menyepadukan inferens sebab ke dalam ramalan trajektori kenderaan. Dalam bidang pemprosesan bahasa semula jadi, penyelidik mendapati bahawa inferens sebab boleh membantu kaedah NLP menjadi lebih mantap dan mudah difahami (Zeng et al. 2020), termasuk menguji bias dalam model bahasa dan korpora (Vig et al. 2020)... I percaya bahawa pada masa hadapan, inferens sebab akan terus berkembang, memainkan peranan penting dalam bidang ini dan lain-lain.

Atas ialah kandungan terperinci Ringkasan idea teknikal utama dan kaedah inferens sebab musabab. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!