Penjelasan terperinci tentang kaedah kawalan yang biasa digunakan untuk perancangan dan kawalan kereta pintar

Kawalan ialah strategi yang memacu kenderaan ke hadapan. Matlamat kawalan adalah untuk menggunakan kuantiti kawalan yang boleh dilaksanakan untuk meminimumkan penyelewengan daripada trajektori sasaran, memaksimumkan keselesaan penumpang, dsb.

Seperti yang ditunjukkan dalam rajah di atas, modul yang dikaitkan dengan input modul kawalan termasuk modul perancangan, modul kedudukan dan maklumat kenderaan, dsb. Modul penentududukan menyediakan maklumat lokasi kenderaan, modul perancangan menyediakan maklumat trajektori sasaran, dan maklumat kenderaan termasuk gear, kelajuan, pecutan, dsb. Output kawalan ialah kuantiti stereng, pecutan dan brek.

Modul kawalan terbahagi terutamanya kepada kawalan mendatar dan kawalan menegak Mengikut bentuk gandingan yang berbeza, ia boleh dibahagikan kepada dua kaedah: bebas dan bersepadu.

1 Kaedah kawalan

1.1 Kawalan penyahgandingan

Jadi- dipanggil Decoupled control bermaksud mengawal kaedah kawalan mendatar dan menegak secara bebas.

1.2 Kawalan gandingan

Kawalan gandingan mengambil kira masalah gandingan yang wujud dalam kawalan mendatar dan menegak. Contoh biasa ialah kereta tidak boleh membelok pada kelajuan tinggi kerana apabila kelajuan membujur terlalu tinggi, kelajuan sudut sisi perlu dihadkan, jika tidak daya sentripetal tidak dapat memenuhi pecutan sentripetal.

Kaedah perwakilan tipikal penyepaduan mendatar dan menegak ialah kawalan ramalan model pembolehubah masa linear Kaedah ini menambah penyepaduan mendatar dan menegak berdasarkan kawalan ramalan model. Seperti kekangan pecutan sentripetal maksimum, dsb.

1.3 Kawalan sisi

Seperti yang ditunjukkan di atas, kawalan sisi boleh dibahagikan kepada kaedah geometri dan kinematik kaedah berasaskan model dan kaedah berasaskan model dinamik.

1.3.1 Kawalan maklum balas

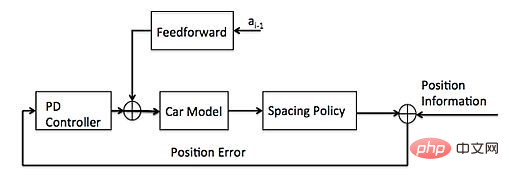
Apa yang dipanggil kawalan suapan hadapan adalah berdasarkan maklumat titik penjejakan . Kawal jumlah untuk membuat pampasan yang sesuai terlebih dahulu. Contoh biasa ialah menggunakan maklumat kelengkungan dalam titik jujukan penjejakan untuk mengimbangi sudut putaran.

1.3.2 Bentuk Berantai

Sistem berantai melakukan pelinearan berbilang lapisan bagi sistem tak linear, yang menguraikan sistem lapisan demi lapisan. Sebaliknya, sistem boleh diperlahankan, sama seperti sistem penapisan [3].

Model sistem dalam koordinat frenet:

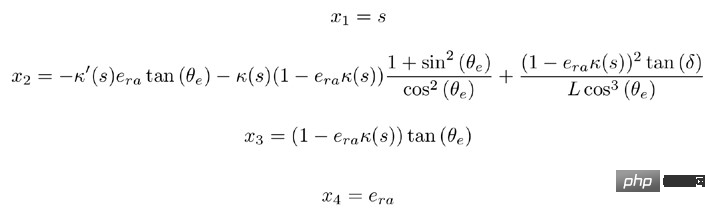
Selepas belanjawan kamiran terbalik, kadar kawalan boleh diperoleh:

1.3.3 Lyapunov

Berasaskan pada Lyapunov Reka bentuk kaedah kestabilan Nove boleh digunakan untuk model kinematik dan dinamik. Idea asas adalah untuk mula-mula mewujudkan model kinematik atau dinamik, mencadangkan kaedah penjejakan berdasarkan model, dan kemudian mewujudkan fungsi Lyapunov untuk membuktikan kestabilan asimptotik sistem gelung tertutup melalui kestabilan Lyapunov [4].

• Model kinematik

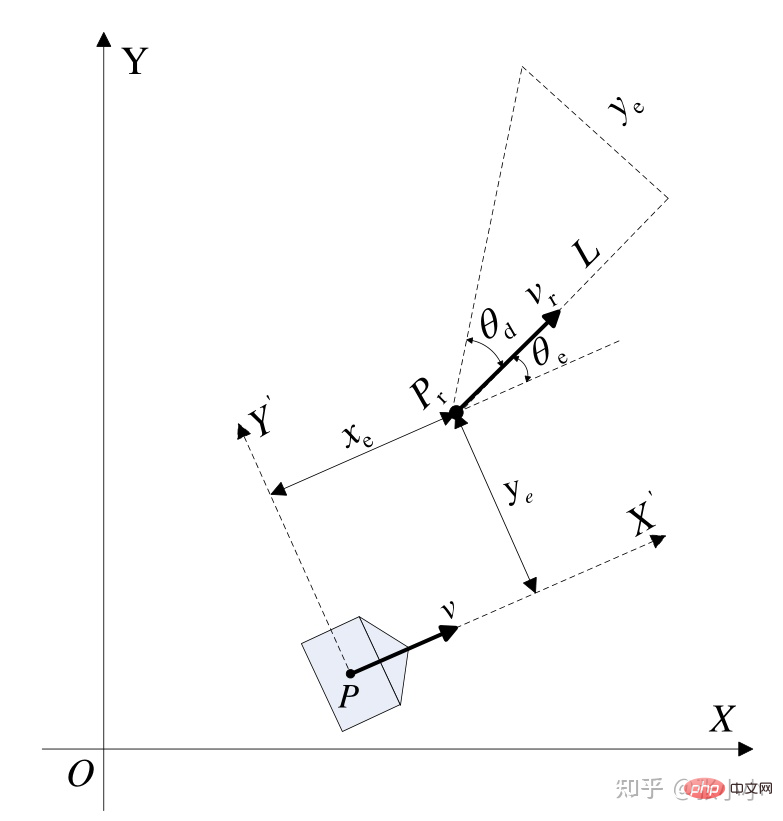
Seperti yang ditunjukkan dalam rajah di atas, titik semasa kereta ialah P , menjejak titik sasaran Untuk Pr. ialah perbezaan pose antara kedudukan semasa dan titik sasaran, dan masing-masing ialah halaju rujukan dan halaju sudut. Fungsi Lyapunov Reka Bentuk:

Reka bentuk kadar penjejakan:

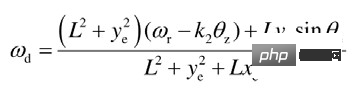
Akhir sekali, dengan mengehadkan parameter reka bentuk kekangan, kestabilan asimptotik kadar penjejakan dibuktikan, iaitu, apabila → ∞, → 0.

• Model kinematik

Mula-mula wujudkan model kinetik:

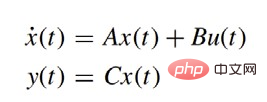
Antaranya:

Ling

Kemudian ralatnya ialah:

Fungsi kos reka bentuk:

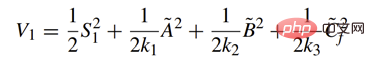
Kadar kawalan reka bentuk:

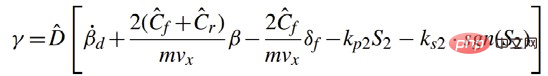
Akhir sekali membuktikan kestabilan asimptotik.

1.3.4 Pursuit Pursuit

Pure Pursuit ialah pengawal penjejakan laluan geometri. Pengawal ini menggunakan hubungan geometri antara gerakan kenderaan dan laluan rujukan untuk menjejaki pengawal laluan rujukan. Kaedah kawalan ini menggunakan bahagian tengah gandar belakang kenderaan sebagai titik rujukan.

Mengikut gambar di atas, arahan pusingan roda hadapan boleh diperolehi:

Di mana R ialah jejari pusingan, L ialah jarak roda kenderaan, e ialah ralat sisi antara sikap semasa kenderaan dan titik laluan sasaran, ialah jarak pandang ke hadapan dan .

Menurut data percubaan dalam rajah di atas, apabila jarak pandang ke hadapan meningkat, jitter penjejakan menjadi lebih kecil dan lebih kecil. Jarak penglihatan hadapan yang lebih pendek menyediakan penjejakan yang lebih tepat, manakala jarak penglihatan hadapan yang lebih panjang menyediakan penjejakan yang lebih lancar. Satu lagi ciri PurePursuit ialah jarak penglihatan hadapan yang berlebihan boleh menyebabkan "memotong sudut" apabila menjejak selekoh. Pure Pursuit ialah pertukaran sukar antara kestabilan dan prestasi penjejakan.

1.3.5 Stanley

Berbeza dengan kaedah pengejaran tulen dan pengesanan tulen di mana paksi belakang adalah titik rujukan, pengawal Stanley menggunakan paksi hadapan sebagai rujukan titik. Ia mengambil kira kesilapan tajuk dan sisi. Pengawal Stanley bukan sahaja mempertimbangkan ralat tajuk tetapi juga ralat sisi.

Mengikut gambar di atas, arahan pusingan roda hadapan boleh diperolehi:

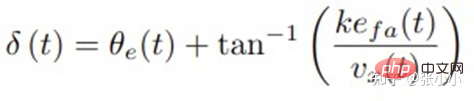
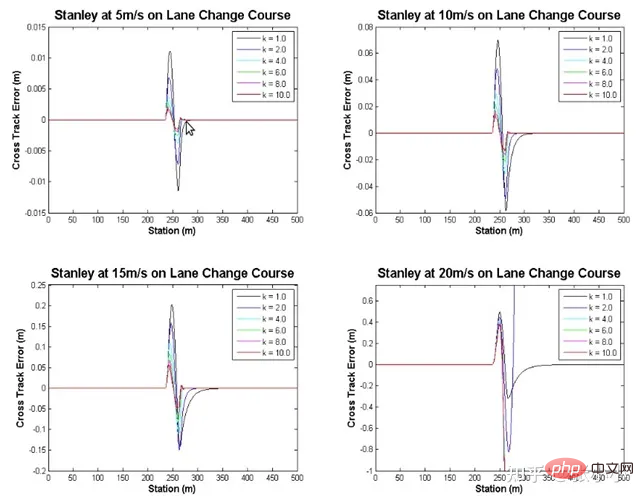
Menurut data percubaan dalam rajah di atas, apabila k meningkat, prestasi penjejakan juga akan bertambah baik. Stanley tidak mempunyai kestabilan yang mencukupi seperti Pure Pursuit apabila kelajuan kenderaan meningkat.

1.3.6 LQR

Kaedah berdasarkan model kinematik kenderaan mengabaikan ciri-ciri dinamik kenderaan, jadi apabila kelajuan kenderaan adalah terlalu laju atau kelengkungan Apabila kadar perubahan terlalu besar, algoritma tidak dapat memenuhi keperluan kawalan kestabilan kenderaan. Untuk kaedah kawalan berdasarkan model dinamik kenderaan, tugas utama adalah untuk memodelkan dinamik kenderaan. Memandangkan model dinamik dua darjah kebebasan yang tepat adalah tak linear, untuk memudahkan pengiraan kawalan penjejakan masa nyata, biasanya perlu membuat beberapa anggaran yang dipermudahkan berdasarkan model dinamik dua darjah kebebasan yang tepat untuk mendapatkan model dinamik dua darjah kebebasan linear.

• Model dinamik dua darjah kebebasan kenderaan:

• LQR:

Pengawal Selia Kuadratik Linear (LQR) ialah pengawal berasaskan model yang menggunakan keadaan kenderaan untuk meminimumkan ralat. Teori LQR ialah kaedah reka bentuk ruang keadaan yang paling awal dan paling matang dalam teori kawalan moden. LQR boleh mendapatkan undang-undang kawalan optimum bagi maklum balas linear keadaan dan mudah untuk membentuk kawalan optimum gelung tertutup.

Reka bentuk optimum LQR bermakna pengawal maklum balas keadaan reka bentuk K harus meminimumkan fungsi objektif kuadratik J, dan K ditentukan secara unik oleh matriks berat Q dan R, jadi Pilihan Q dan R amat penting. Formula berikut ialah fungsi kos LQR:

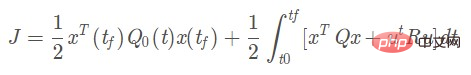
Menurut model dinamik kenderaan dan fungsi kos LQR, persamaan Licati algebra boleh diterbitkan:

Akhir sekali, matriks maklum balas dikira melalui persamaan Ricati berulang, dan jumlah kawalan optimum diperoleh berdasarkan matriks maklum balas.

1.3.7 MPC

MPC (Model Prediction Control) ialah kaedah yang dikhususkan untuk meramalkan jangka masa yang lebih panjang, malah masa yang tidak terhingga Kawalan optimum masalah diuraikan kepada beberapa masalah kawalan pengoptimuman dengan jangka masa yang lebih pendek atau jangka masa terhad, dan penyelesaian optimum masih diteruskan pada tahap tertentu.

MPC terdiri daripada tiga elemen berikut:

1. Model ramalan: Model ramalan boleh meramalkan perubahan dalam status sistem dengan baik dalam tempoh masa yang singkat;
2. Pengoptimuman rolling dalam talian: Keputusan yang diperolehi oleh model ramalan Masih terdapat sisihan daripada realiti, jadi pengoptimuman rolling digunakan untuk mencari penyelesaian optimum setempat pada setiap saat Biasanya, fungsi sasaran (kerugian) direka bentuk dan ditukar kepada masalah pengaturcaraan kuadratik untuk mencari penyelesaian optimum; >
3. Pembetulan Maklum Balas: Ramal semula dan optimumkan berdasarkan status baharu pada masa berikutnya.

• Model ramalan:

Model ramalan boleh diterbitkan berdasarkan model dinamik kenderaan dalam LQR .

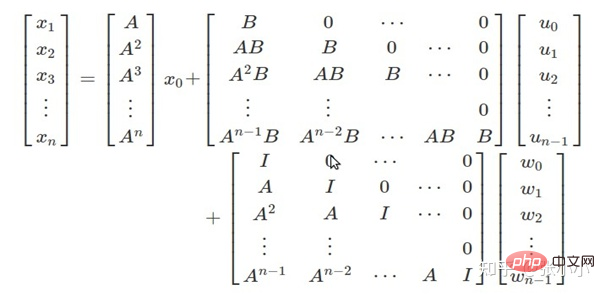
• Pengoptimuman tatal:

Fungsi kos MPC:

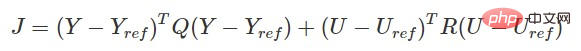
Arahan kawalan yang sepadan boleh diperolehi dengan mengoptimumkan penyelesaian berdasarkan model ramalan, kekangan sisi kenderaan dan fungsi kos .

1.3.8 Perbandingan algoritma kawalan mendatar

1.4 Menegak

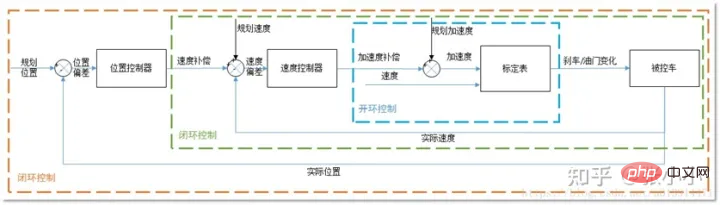
Seperti yang ditunjukkan dalam rajah di atas, kawalan menegak secara amnya menggunakan kaedah kawalan pid cascade.

2 Reka Bentuk Terperinci

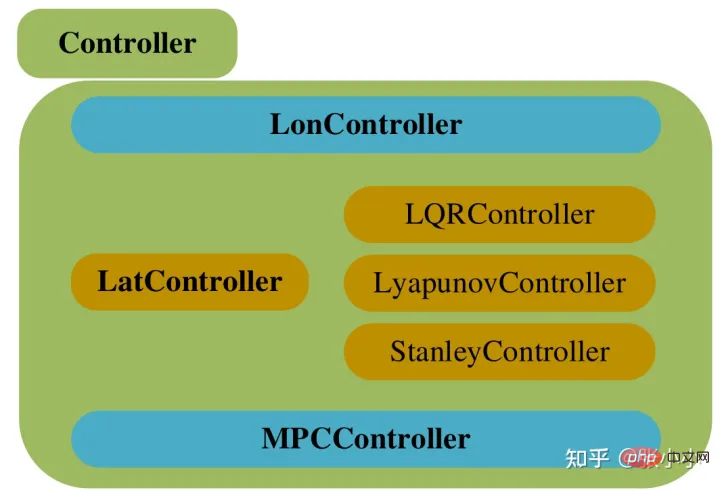
Reka bentuk pengawal adalah seperti yang ditunjukkan dalam gambar di atas, di mana Pengawal Sebagai kelas asas, LonController, LonController dan MPCController mewarisi kelas asas ini. LonController telah memperoleh subkelas seperti LQRController, LyapunovController dan StanleyController.

Atas ialah kandungan terperinci Penjelasan terperinci tentang kaedah kawalan yang biasa digunakan untuk perancangan dan kawalan kereta pintar. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!