13 taburan kebarangkalian yang mesti dikuasai dalam pembelajaran mendalam

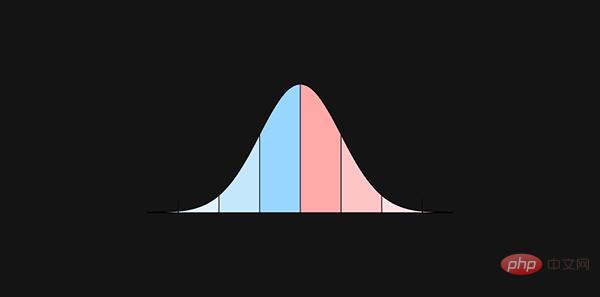
1. Gambaran keseluruhan taburan kebarangkalian

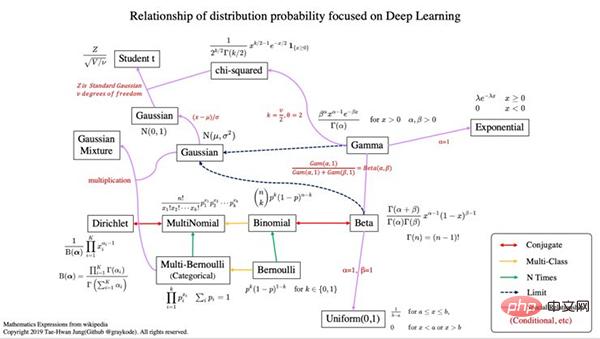
• Konjugat bermaksud ia mempunyai hubungan taburan konjugat.
• Dalam teori kebarangkalian Bayesian, jika taburan posterior p(θx) dan taburan kebarangkalian terdahulu p(θ) berada dalam keluarga taburan kebarangkalian yang sama, taburan awal dan posterior dipanggil taburan konjugat, Sebelum dipanggil taburan konjugat sebelum fungsi kemungkinan. Conjugate prior Wikipedia ada di sini (https://en.wikipedia.org/wiki/Conjugate_prior).
• Pengkelasan berbilang bermakna varians rawak lebih besar daripada 2.
• n kali bermakna kami juga mempertimbangkan kebarangkalian terdahulu p(x).
• Untuk mengetahui lebih lanjut tentang kebarangkalian, saya mengesyorkan membaca [pengiktirafan pola dan pembelajaran mesin, Bishop 2006].

2. Kebarangkalian dan ciri taburan

1. Taburan seragam (berterusan)

Kod: https://github.com/graykode/distribution-is-. all-you-need/blob/master/uniform.py

Taburan seragam mempunyai nilai kebarangkalian yang sama pada [a, b] dan merupakan taburan kebarangkalian mudah.

2. Taburan Bernoulli (diskrit)

Kod: https://github.com/graykode/distribution-is-all-you- need/ blob/master/bernoulli.py

• Kebarangkalian terdahulu p(x) tidak mengambil kira taburan Bernoulli. Oleh itu, jika kita mengoptimumkan untuk kebarangkalian maksimum, kita boleh dengan mudah menjadi berlebihan.
• Menggunakan entropi silang binari untuk mengelaskan pengelasan binomial. Bentuknya adalah sama dengan logaritma negatif taburan Bernoulli. Gambar

3. Taburan binomial (diskrit)

Kod: https://github.com/graykode/distribution-is-all-you-need/blob/master/ binomial .py

• Taburan binomial dengan parameter n dan p ialah taburan kebarangkalian diskret bagi bilangan kejayaan dalam satu siri n eksperimen bebas.
• Taburan binomial ialah taburan yang mengambil kira kebarangkalian terdahulu dengan menyatakan kuantiti yang akan dipilih terlebih dahulu.

4. Pengagihan berbilang Bernoulli, pengedaran kategori (diskrit)

Kod: https://github.com/graykode/distribution - is-all-you-need/blob/master/categorical.py

• Bernoulli Berbilang dipanggil pengedaran kategori.
• Entropi silang mempunyai bentuk yang sama seperti taburan berbilang Bernoulli yang mengambil logaritma negatif.

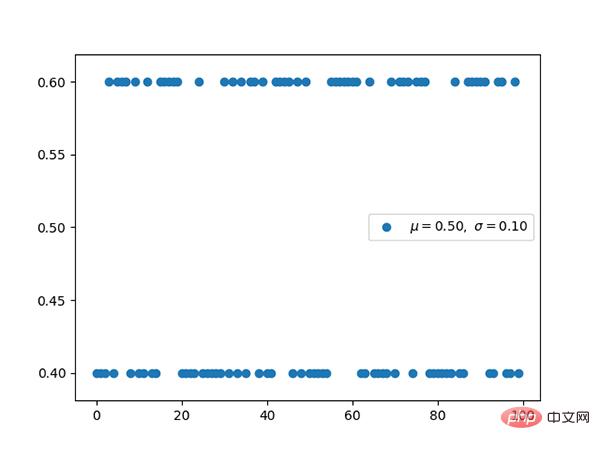
5. Taburan polinomial (diskrit)

Kod: https://github.com/graykode/distribution-is-all-you -need/blob/master/multinomial.py

Hubungan antara taburan polinomial dan taburan kategori adalah sama seperti hubungan antara taburan Bernoul dan taburan binomial.

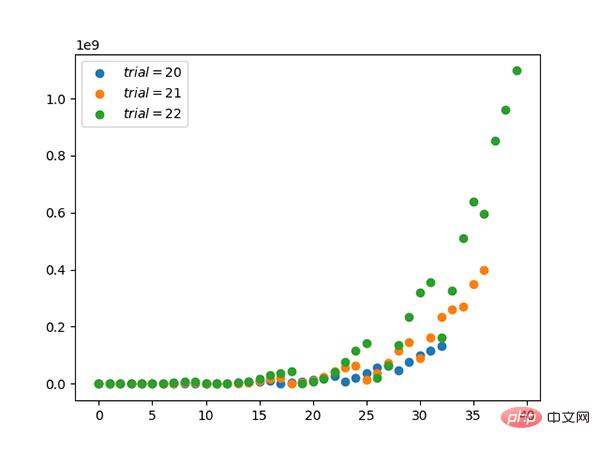
Pengedaran 6.β (berterusan)

Kod: https://github.com/graykode/distribution-is-all-you-need/ blob/master/beta.py

• Taburan beta adalah konjugat kepada taburan binomial dan Bernoulli.
• Menggunakan konjugasi, taburan posterior boleh diperolehi dengan lebih mudah menggunakan taburan terdahulu yang diketahui.
• Apabila taburan β memenuhi kes khas (α=1, β=1), taburan seragam adalah sama.

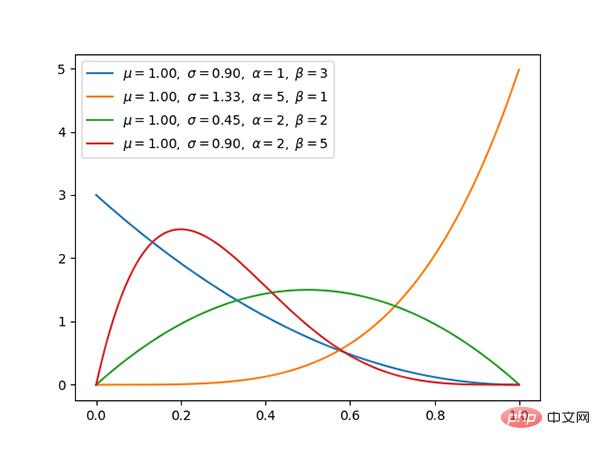
7.Pengedaran Dirichlet (berterusan)

Kod: https://github.com/graykode/distribution-is-all-you -need/blob/master/dirichlet.py

• Taburan dirichlet adalah konjugat kepada taburan polinomial.
• Jika k=2, ia adalah pengedaran beta.

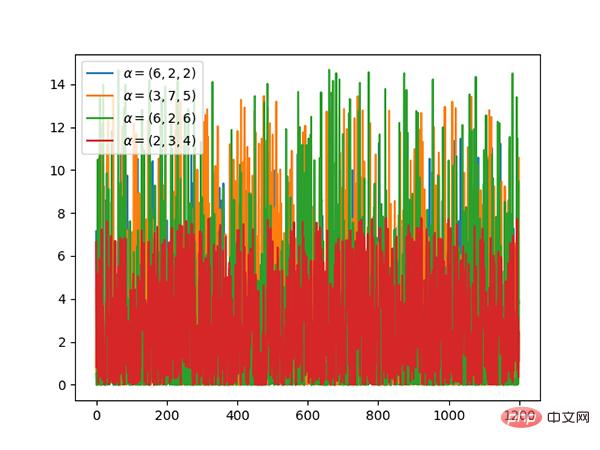
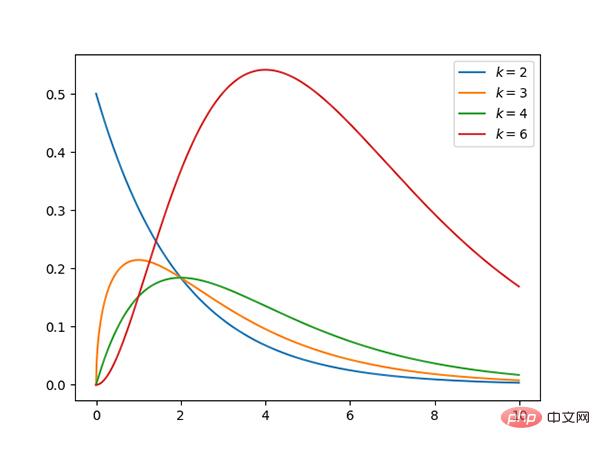
8 Pengagihan gamma (berterusan)

Kod: https://github.com/graykode/distribution-is-all- you. -need/blob/master/gamma.py

• Jika gamma(a,1)/gamma(a,1)+gamma(b,1) adalah sama dengan beta(a,b) , Maka taburan gamma ialah taburan beta.
• Taburan eksponen dan taburan khi kuasa dua ialah kes khas taburan gamma.

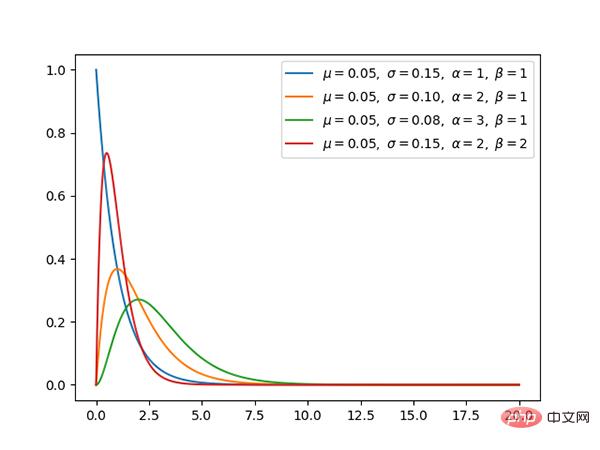
9. Taburan eksponen (berterusan)

Kod: https://github.com/graykode/distribution-is-all-you -need/blob/master/exponential.py

Taburan eksponen ialah kes khas taburan γ apabila α ialah 1.

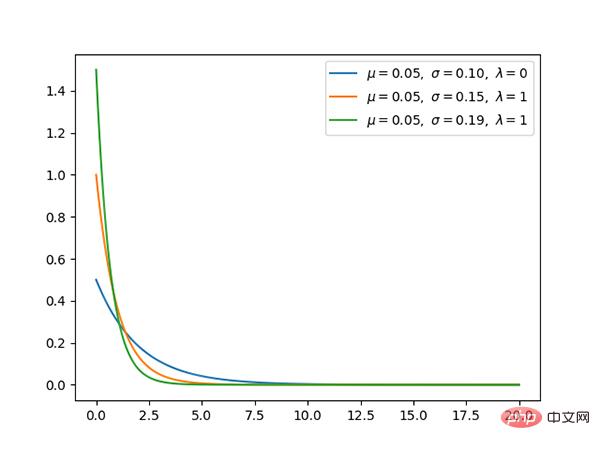
10 Taburan Gaussian (berterusan)

Kod: https://github.com/graykode/distribution-is-all-you-need/ blob/master/gaussian.py

Taburan Gaussian ialah taburan kebarangkalian berterusan yang sangat biasa.

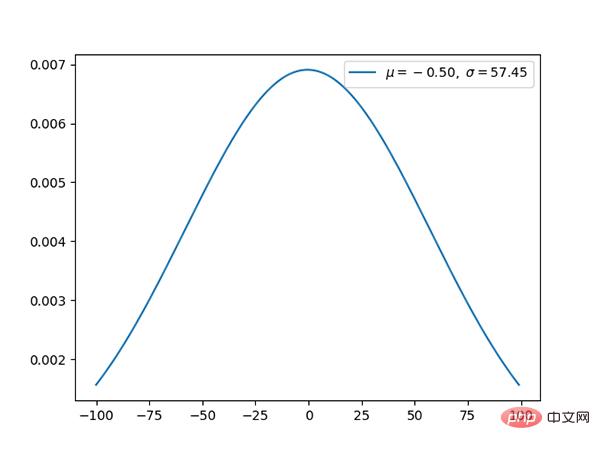
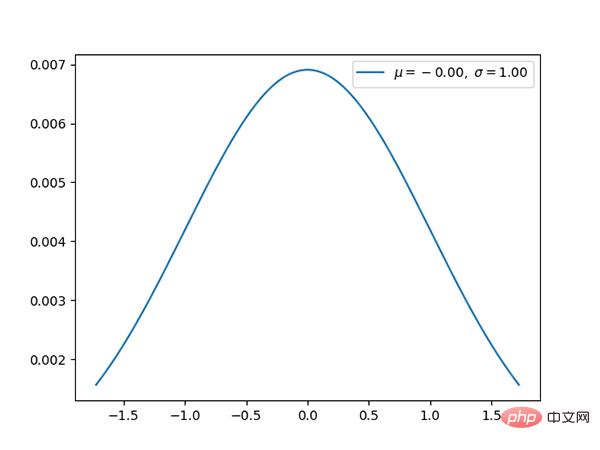
11 Taburan normal (berterusan)

Kod: https://github.com/graykode/distribution-is-all-you-need / blob/master/normal.py

Taburan normal ialah taburan Gaussian piawai, dengan min 0 dan sisihan piawai 1.

12 Taburan Chi-square (berterusan)

Kod: https://github.com/graykode/distribution-is-all-you- need /blob/master/chi-squared.py

• Taburan khi kuasa dua dengan k darjah kebebasan ialah taburan hasil tambah kuasa dua k pembolehubah rawak normal piawai bebas.
• Taburan Chi-square ialah kes khas taburan beta

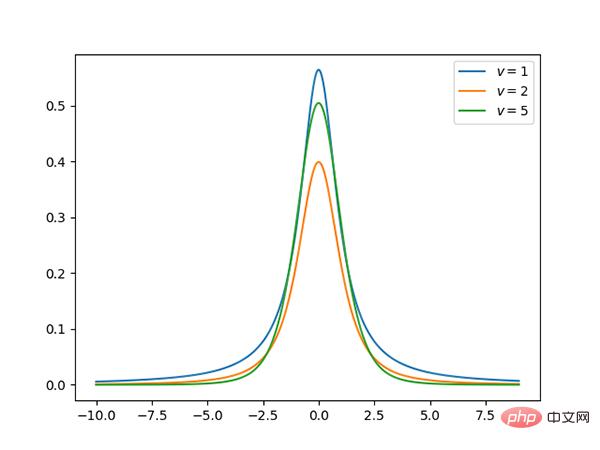
Taburan 13.t (berterusan)

Kod: https:///github.com/graykode/distribution-is-all-you-need/blob/master/student-t.py

t Taburan ialah taburan berbentuk loceng simetri, serupa dengan biasa pengedaran, tetapi dengan ekor yang lebih panjang Heavy, yang bermaksud ia lebih berkemungkinan menghasilkan nilai jauh di bawah purata.

melalui: https://github.com/graykode/distribution-is-all-you-needa

Atas ialah kandungan terperinci 13 taburan kebarangkalian yang mesti dikuasai dalam pembelajaran mendalam. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!