Rumah >Peranti teknologi >AI >Teka-teki dari 60 tahun yang lalu! Penyelidik dari Universiti Copenhagen menyelesaikan masalah 'jalan terpendek sumber tunggal'.
Teka-teki dari 60 tahun yang lalu! Penyelidik dari Universiti Copenhagen menyelesaikan masalah 'jalan terpendek sumber tunggal'.
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-11 20:04:181344semak imbas
"Dalam graf berwajaran G=(V,E), berat setiap tepi ialah nombor nyata. Selain itu, bucu dalam V juga diberikan, dipanggil sumber.
Kira panjang laluan terpendek dari punca ke semua bucu lain Ini ialah masalah laluan terpendek sumber tunggal (SSSP). >
Selama lebih setengah abad, penyelidik di seluruh dunia telah berusaha untuk menyelesaikan masalah ini. Kini, teka-teki algoritma ini akhirnya berjaya diselesaikan oleh pasukan penyelidik dari Jabatan Sains Komputer di Universiti Copenhagen.Algoritma SSSP berat negatif: pantas dan cekap

Dalam temu bual, penyelidik Christian Wulff-Nilsen berkata bahawa penyelesaian mereka adalah kejayaan pertama yang telah wujud selama lebih daripada 30 tahun
Õ(n(4/3) log W) kekangan masa operasi ialah algoritma gabungan SSSP dengan pemberat negatif.
Terdapat dua algoritma klasik tentang SSSP: algoritma Dijkstra (algoritma Dijkstra) dan algoritma Bellman-Ford (algoritma Bellman-Ford), kedua-duanya Semua mempunyai had mereka sendiri .Algoritma Dijkstra mempunyai masa operasi terpendek dan boleh mencapai masa hampir linear
O(m + n log n), tetapi tepi berat negatif tidak boleh dikira.
Algoritma Bellman-Ford boleh mengira tepi berat negatif, tetapi masa operasi terlalu lama, mencecahO(mn). Pada masa ini, algoritma SSSP tercanggih untuk menyelesaikan tepi berwajaran negatif bergantung pada pengoptimuman berterusan yang kompleks dan algoritma algebra dan grafik dinamik. Ini membawa kepada fakta bahawa walaupun generasi sarjana terkemudian terus mengoptimumkan algoritma, masa pengiraannya masih memerlukan Õ(n(4/3) log W). Kekangan masa pengiraan ini telah wujud selama tiga puluh tahun.
Menghadapi batasan ini, Wulff-Nilsen menimbulkan dua soalan:1) Bolehkah operasi algoritma kelebihan berwajaran negatif mencapai masa hampir linear?
2) Bolehkah ini dicapai dengan alatan mudah?
Adakah terdapat kaedah yang memerlukan masa dan kualiti?
Jangan beritahu saya, ia benar-benar wujud.
Algoritma yang dicadangkan oleh Wulff-Nilsen ialah algoritma penskalaan imej, yang dipertingkatkan oleh algoritma penguraian imej ringkas Penguraian Diameter Rendah. Biasanya, algoritma penguraian ini hanya digunakan untuk penguraian graf bagi tepi bukan berwajaran negatif, dan salah satu sumbangan penyelidikan ini adalah untuk mengaplikasikannya pada imej tepi berwajaran negatif untuk mengukuhkan algoritma penskalaan rekursif SSSP tepi berwajaran negatif.
Proses derivasi
Wulff-Nilsen adalah berdasarkan algoritma harga Johnson. Cadangkan: Dalam imejG = (V, E, w), biarkan Φ menjadi sebarang fungsi: V→ Z. Biarkan w(Φ) menjadi fungsi berat:
takrif: , : . Dalam imejG = (V, E,w) dan imej G' = (V, E,w'), jika: 1) Jarak terpendek dalam imej G ialah The jarak terpendek dalam imej G' adalah sama dan begitu juga sebaliknya; ' Apabila mengandungi cincin berat negatif, imej G adalah sama dengan imej G'. Corollary 2.7 Pertimbangkan sebarang imej
dan fungsi harga Φ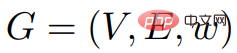 . Dalam u, v ∈ V, . Dan dalam mana-mana cincin
. Dalam u, v ∈ V, . Dan dalam mana-mana cincin
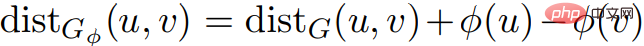 , . Oleh itu,
, . Oleh itu,
G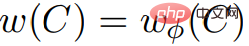 dan adalah sama. Jika
dan adalah sama. Jika 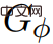 , , maka
, , maka 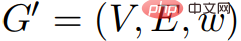
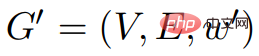 G
G dan G' adalah sama. Tujuan algoritma ini adalah untuk mengira fungsi harga
dan G' adalah sama. Tujuan algoritma ini adalah untuk mengira fungsi harga
apabila GΦ adalah bukan negatif, dengan mengandaikan tiada kitaran berat negatif. Kemudian anda boleh menjalankan algoritma Dijkstra pada . 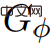 Selepas itu, Wulff-Nilsen mula memperkenalkan rangka kerja algoritmanya.
Selepas itu, Wulff-Nilsen mula memperkenalkan rangka kerja algoritmanya.
Pertama, Wulff-Nilsen mengandaikan bahawa terdapat algoritma Dijkstra (G, s), memasukkan graf tanpa tepi berat negatif G
, bucus ∈ V, s dalam G mengeluarkan pepohon laluan terpendek. Masa berjalan ialah O(m + n log n). Jika G ialah DAG (graf asiklik berarah), hitung fungsi harga Φ supaya Matlamat masalah laluan terpendek sumber tunggal adalah untuk mencari laluan terpendek dari nod permulaan yang diberikan kepada semua nod lain dalam rangkaian. Rangkaian diwakili sebagai graf yang terdiri daripada nod dan sambungan antara mereka, dipanggil tepi. Setiap tepi mempunyai arah (contohnya, ini boleh digunakan untuk mewakili jalan sehala) dan berat yang mewakili kos perjalanan sepanjang itu tepi. Jika semua pemberat tepi adalah bukan negatif, masalah itu boleh diselesaikan dalam masa yang hampir linear menggunakan algoritma Dijkstra klasik. Keputusan baharu menyelesaikan masalah ini dalam masa yang hampir sama dengan algoritma Dijkstra, tetapi juga membenarkan pemberat kelebihan negatif. Selepas itu, Wulff-Nilsen menyebut dua algoritma paling penting dalam alatan gabungan: ScaleDown dan SPmain . Algoritma ScaleDown berjalan secara berperingkat, dan pada peringkat terakhir ia menggunakan ElimNeg ( Ini bermakna untuk semua Jika algoritma ditamatkan, maka untuk semua Ini bermakna untuk semua Dengan aruhan, dengan mengandaikan bahawa teori itu berlaku untuk Oleh itu, melalui Output Sejak Ini boleh membuktikan ketepatan algoritma SPmain. Pada ketika ini, dua algoritma paling penting dalam penyelesaian SSSP berat negatif Wulff-Nilsen telah terbukti benar. Algoritma baharu berjaya memperkenalkan pemberat negatif sambil memastikan masa hampir linear. 60 tahun kemudian, pencarian jawapan bukan sekadar teka-teki Beliau percaya bahawa menyelesaikan masalah SSSP boleh membuka jalan kepada algoritma yang bukan sahaja dapat membantu kenderaan elektrik mengira dengan serta-merta laluan terpantas ke destinasi mereka, tetapi juga memastikan bahawa Cara paling cekap tenaga untuk melakukan ini. Wulff-Nilsen menjelaskan: “Algoritma kami menambah pemberat negatif, satu dimensi yang tidak dimiliki oleh algoritma sebelumnya adalah apabila memandu di pergunungan. dengan dimensi berat negatif, sistem navigasi boleh mengesyorkan laluan dengan banyak jalan menurun untuk pemilik kenderaan elektrik, supaya kenderaan elektrik boleh dicas semasa menuruni bukit >Wulff-Nilsen juga berkata bahawa algoritma mereka bukan sahaja boleh digunakan untuk kenderaan elektrik perancangan laluan, tetapi juga untuk memantau spekulasi dalam industri kewangan. Beliau berkata: "Secara prinsipnya, algoritma ini boleh digunakan untuk memberi amaran awal kepada pengguna seperti bank pusat, memberi amaran kepada spekulator yang membuat spekulasi dalam pembelian dan penjualan pelbagai mata wang. Kini, ramai penjenayah menggunakan komputer untuk melakukan jenayah, tetapi kerana algoritma kami adalah begitu pantas, mungkin Ia digunakan untuk memantau dan mengesan kelemahan sebelum ia dieksploitasi Pada tahun 1959, apabila Dijkstra mula-mula mencadangkan masalah jarak terpendek, dia mungkin tidak memikirkannya selama lebih daripada 60 tahun telah sentiasa mengoptimumkan penyelesaian kepada masalah ini. Anda juga mungkin terkejut bahawa jawapan kepada teka-teki itu mempunyai konotasi yang begitu kaya. Mungkin, inilah daya tarikan sains. 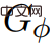 Mempunyai bukan -berat tepi negatif adalah mudah: hanya gelung pada v1, ..., vn topologi dan tetapkan Φ(vi) supaya semua pemberat tepi masuk adalah bukan negatif.
Mempunyai bukan -berat tepi negatif adalah mudah: hanya gelung pada v1, ..., vn topologi dan tetapkan Φ(vi) supaya semua pemberat tepi masuk adalah bukan negatif. 
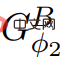 ) untuk mengira fungsi hargaΦ2. Jika ElimNeg ditamatkan, ia akan mengembalikan fungsi harga ψ′, biarkan
) untuk mengira fungsi hargaΦ2. Jika ElimNeg ditamatkan, ia akan mengembalikan fungsi harga ψ′, biarkan 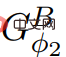 semua nilai tepi tidak Negatif; dengan kata lain, kerana
semua nilai tepi tidak Negatif; dengan kata lain, kerana 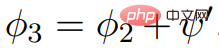 , , oleh itu
, , oleh itu 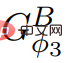 tidak mengandungi pemberat negatif.
tidak mengandungi pemberat negatif. 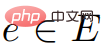 ,
, 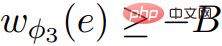 memenuhi syarat (kerana
memenuhi syarat (kerana 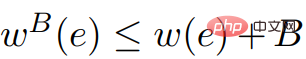 ). Ini membuktikan ketepatan output ScaleDown.
). Ini membuktikan ketepatan output ScaleDown. 
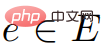 dan
dan 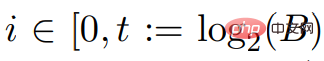 ,
, 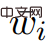 adalah integral dan untuk semua
adalah integral dan untuk semua 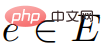 ,
,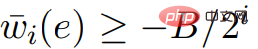 .
. 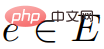 ,
, 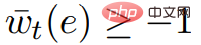 . Oleh itu graf G* mempunyai pemberat bukan negatif.
. Oleh itu graf G* mempunyai pemberat bukan negatif. 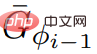 , untuk ScaleDown dalam baris 5 daripada algoritma Panggilan ke
, untuk ScaleDown dalam baris 5 daripada algoritma Panggilan ke 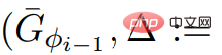
 memenuhi atribut input yang diperlukan.
memenuhi atribut input yang diperlukan. 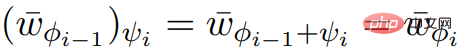 dan ScaleDown, anda boleh mendapatkan
dan ScaleDown, anda boleh mendapatkan 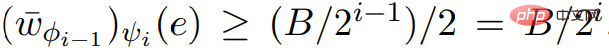 .
. 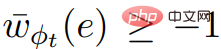 , jika biar C menjadi
, jika biar C menjadi 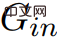 untuk sebarang kitaran berat negatif dalam
untuk sebarang kitaran berat negatif dalam  , kerana semua nilai dalam
, kerana semua nilai dalam 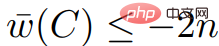 ialah gandaan 2n, dan ;
ialah gandaan 2n, dan ; 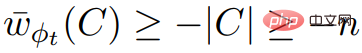 Kami juga tahu bahawa ,
Kami juga tahu bahawa , 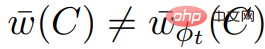 , jadi
, jadi  Oleh itu kita boleh membuat kesimpulan bahawa jika
Oleh itu kita boleh membuat kesimpulan bahawa jika
Atas ialah kandungan terperinci Teka-teki dari 60 tahun yang lalu! Penyelidik dari Universiti Copenhagen menyelesaikan masalah 'jalan terpendek sumber tunggal'.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

