Rumah >Peranti teknologi >AI >Bagaimana untuk menggunakan data dengan lebih baik dalam inferens sebab-akibat?
Bagaimana untuk menggunakan data dengan lebih baik dalam inferens sebab-akibat?
- PHPzke hadapan
- 2023-04-11 19:43:021611semak imbas

Pengenalan: Tajuk perkongsian ini ialah "Bagaimana untuk menggunakan data dengan lebih baik dalam inferens sebab-akibat? " ", yang terutamanya memperkenalkan kerja terbaru pasukan berkaitan dengan kertas kerja yang diterbitkan mengenai sebab dan akibat. Laporan ini memperkenalkan cara kami boleh menggunakan lebih banyak data untuk membuat inferens sebab dari dua aspek Satu ialah menggunakan data kawalan sejarah untuk secara jelas mengurangkan bias kekeliruan, dan satu lagi ialah inferens sebab di bawah gabungan data berbilang sumber.
Jadual kandungan teks penuh:
- Latar belakang inferens sebab
- Pohon Penyebab Pembetulan GBCT
- Penyatuan Data Penyebab
- Aplikasi perniagaan dalam Ant
1 Latar belakang inferens sebab
Masalah ramalan pembelajaran mesin biasa. secara amnya Apabila ditetapkan dalam sistem yang sama, taburan bebas dan serupa biasanya diandaikan, seperti meramalkan kebarangkalian kanser paru-paru dalam kalangan perokok, klasifikasi gambar dan masalah ramalan lain. Persoalan penyebab adalah berkaitan dengan mekanisme di sebalik data soalan biasa seperti "Adakah merokok menyebabkan kanser paru-paru?"
Terdapat dua jenis data yang sangat penting dalam masalah anggaran kesan sebab akibat: satu jenis ialah data pemerhatian, dan jenis lain ialah data eksperimen yang dijana secara rawak eksperimen terkawal.
- Data pemerhatian ialah data terkumpul dalam kehidupan atau produk sebenar kita. Sebagai contoh, data merokok menunjukkan bahawa sesetengah orang suka merokok, manakala data pemerhatian adalah berkaitan dengan perokok Pada akhirnya, sebahagian daripada perokok akan mendapat kanser. Masalah ramalan pembelajaran mesin adalah untuk menganggarkan kebarangkalian bersyarat P (dapat kanser paru-paru | merokok), iaitu, memandangkan keadaan merokok, kebarangkalian untuk memerhatikan perokok mendapat kanser paru-paru. Dalam data pemerhatian di atas, taburan merokok sebenarnya tidak rawak: keutamaan setiap orang untuk merokok adalah berbeza, dan ia juga dipengaruhi oleh persekitaran.
- Cara terbaik untuk menjawab soalan sebab akibat adalah dengan menjalankan eksperimen terkawal rawak. Data eksperimen diperoleh melalui eksperimen terkawal rawak. Dalam percubaan terkawal rawak, tugasan kepada rawatan adalah rawak. Katakan anda perlu menjalankan eksperimen untuk mendapatkan kesimpulan "sama ada merokok menyebabkan kanser paru-paru Pertama, anda perlu mencari orang yang mencukupi, memaksa separuh daripada mereka untuk merokok, dan memaksa separuh lagi untuk tidak merokok, dan perhatikan kebarangkalian paru-paru." kanser dalam dua kumpulan. Walaupun percubaan terkawal rawak tidak boleh dilakukan dalam beberapa senario disebabkan oleh faktor seperti etika dan dasar, percubaan terkawal rawak masih boleh dijalankan dalam beberapa bidang, seperti ujian A/B dalam promosi carian.

Masalah anggaran sebab masalah E(Y|do(X)) dan masalah ramalan atau klasifikasi tradisional Perbezaan utama antara E(Y|X) ialah simbol intervensi yang dicadangkan oleh Judy Pearl muncul dalam keadaan yang diberikan. Campur tangan untuk memaksa pembolehubah X kepada nilai tertentu. Anggaran kesan sebab akibat dalam laporan ini terutamanya merujuk kepada anggaran kesan sebab akibat daripada data pemerhatian.
Bagaimana untuk menggunakan data dengan lebih baik dalam inferens sebab-akibat? Laporan ini akan memperkenalkan topik sedemikian menggunakan kertas kerja terbaru yang diterbitkan oleh dua pasukan sebagai contoh.
- Tugas pertama ialah cara menggunakan data perbandingan sejarah dengan lebih baik. Contohnya, jika acara promosi pemasaran diadakan pada masa tertentu, masa sebelum titik masa ini dipanggil "pra-campur tangan", dan masa selepas titik masa ini dipanggil "selepas campur tangan". Kami berharap dapat mengetahui kesan sebenar campur tangan sebelum kami campur tangan, supaya dapat membantu kami membuat keputusan seterusnya. Sebelum permulaan kempen pemasaran ini, kami mempunyai data prestasi sejarah pengguna Tugas pertama adalah untuk memperkenalkan cara menggunakan data "pra-campur tangan" dengan baik untuk membantu dalam kerja pembetulan data untuk menilai dengan lebih baik kesan intervensi.
- Kerja kedua terutamanya memperkenalkan cara untuk menggunakan data heterogen berbilang sumber dengan lebih baik. Masalah sedemikian sering terlibat dalam pembelajaran mesin Masalah biasa termasuk penyesuaian domain, pembelajaran pemindahan, dsb. Dalam laporan hari ini, kami akan mempertimbangkan penggunaan data heterogen berbilang sumber daripada perspektif kausal, iaitu, dengan mengandaikan bahawa terdapat berbilang sumber data, bagaimana untuk menganggarkan kesan sebab akibat dengan lebih baik.
2. Pokok Punca dan Kesan Pembetulan GBCT
1 >Algoritma pepohon terutamanya terdiri daripada dua modul:
- Kriteria split: Pisahkan nod kepada dua nod anak mengikut kriteria split
- Anggaran parameter: Selepas pemisahan selesai, seperti akhirnya menghentikan pemisahan, ramalkan kesan sebab akibat sampel atau kumpulan baharu pada nod daun berdasarkan kaedah anggaran parameter
beberapa algoritma pokok kausal tradisional berpecah berdasarkan heterogeneity kesan kausal. sub-nod selepas pemisahan akan berbeza dengan ketara, dan perbezaan itu boleh ditangkap melalui pemisahan kesan sebab akibat dalam pengedaran data. Kriteria pembelahan pokok penyebab tradisional, seperti:
- Kriteria pembelahan pokok terangkat adalah untuk memaksimumkan kesan sebab akibat nod anak kiri dan kanan Perbezaan, ukuran beza menggunakan ukuran jarak seperti jarak Euclidean dan KL divergence; dijelaskan secara intuitif sebagai memaksimumkan kuasa dua kesan penyebab . Ia boleh dibuktikan secara matematik bahawa kriteria pemisahan ini adalah bersamaan dengan memaksimumkan varians kesan sebab akibat nod daun. Kaedah anggaran parameter biasa adalah untuk menolak terus hasil purata kumpulan eksperimen daripada hasil purata kumpulan kawalan pada nod daun terbelah sebagai anggaran penyebab kesan. Jika ia adalah eksperimen terkawal rawak, mekanisme peruntukan untuk rawatan adalah rawak, dan perbezaan purata yang dikira daripada ini adalah kesan sebab akibat. Mekanisme peruntukan rawak memastikan taburan data kumpulan eksperimen dan kumpulan kawalan adalah sama, yang dipanggil homogeniti.
- Dalam pokok penyebab, nod kanak-kanak diperolehi dengan membelah bolehkah dijamin bahawa taburan nod anak kiri dan nod anak kanan yang diperolehi oleh pecahan adalah homogen?
Pokok penyebab tradisional dan pokok angkat tidak dapat menjamin bahagian kiri selepas membelah . Taburan nod anak dan nod anak kanan adalah homogen. Oleh itu, anggaran tradisional
yang disebut dalam bahagian sebelumnya adalah berat sebelah.
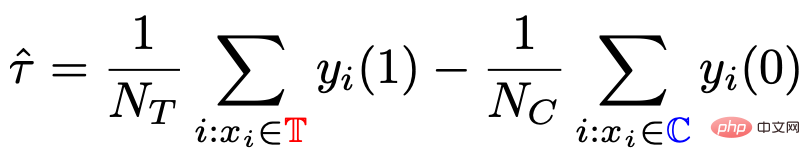 Kerja kami memfokuskan pada menganggarkan purata kesan sebab akibat CATT ke atas kumpulan eksperimen (kumpulan rawatan). CATT ditakrifkan sebagai:
Kerja kami memfokuskan pada menganggarkan purata kesan sebab akibat CATT ke atas kumpulan eksperimen (kumpulan rawatan). CATT ditakrifkan sebagai:
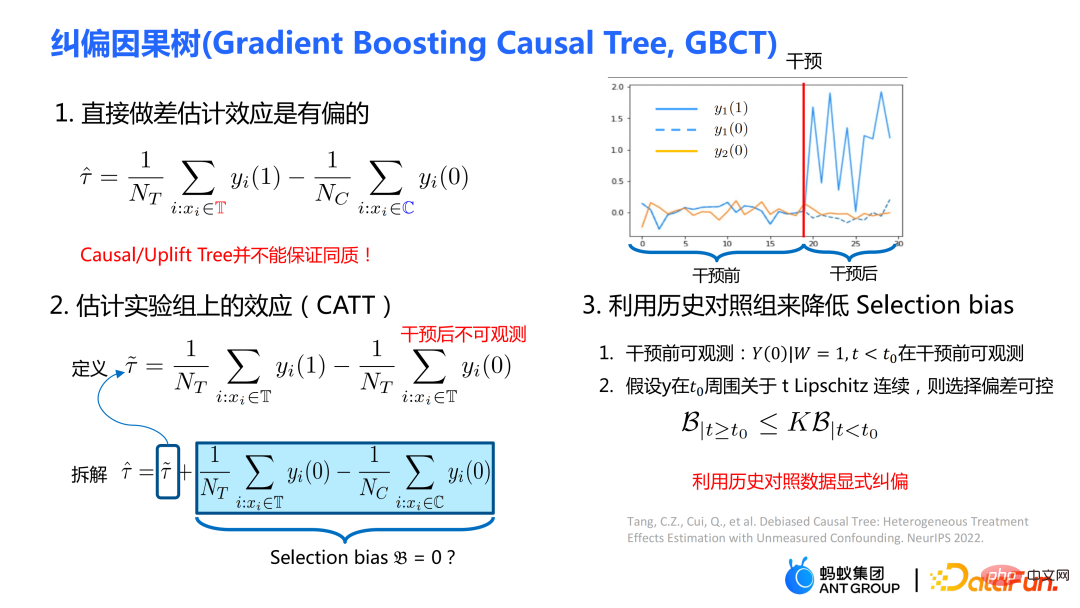
Selanjutnya, anggaran kesan sebab akibat tradisional boleh dibahagikan kepada dua bahagian:
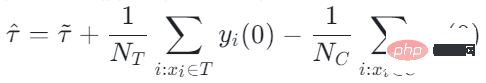
Pincang pilihan/confounding bias boleh ditakrifkan sebagai:
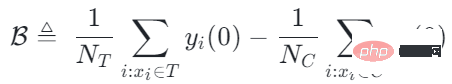
Makna intuitif ialah nilai anggaran apabila rawatan=0 dalam kumpulan eksperimen, tolak nilai anggaran apabila rawatan=0 dalam kumpulan kawalan. Dalam pokok penyebab tradisional, bias di atas tidak dicirikan, dan bias pemilihan mungkin menjejaskan anggaran kami, menyebabkan anggaran akhir menjadi berat sebelah.
Idea kami ialah menggunakan data kawalan sejarah yang terkumpul pada produk atau platform untuk mengurangkan kecenderungan pemilihan secara eksplisit. Operasi khusus adalah berdasarkan dua andaian:
- Andaian 1: Prestasi hasil kumpulan eksperimen dan kumpulan kawalan dalam keadaan rawatan=0 sebelum intervensi boleh diperhatikan . Ambil operasi peningkatan had produk kad kredit dalam produk kredit kewangan sebagai contoh Sebelum peningkatan had, kita boleh melihat prestasi penggunaan biasa pengguna, iaitu prestasi hasil kumpulan eksperimen dan kumpulan kawalan tanpa meningkatkan had (rawatan. =0) tersedia;
- Andaian 2: Andaikan bahawa y hasil memenuhi kesinambungan tertentu sebelum dan selepas intervensi. Pemahaman intuitif ialah perubahan dalam tingkah laku pengguna atau kumpulan tidak akan terlalu drastik sebelum dan selepas intervensi.
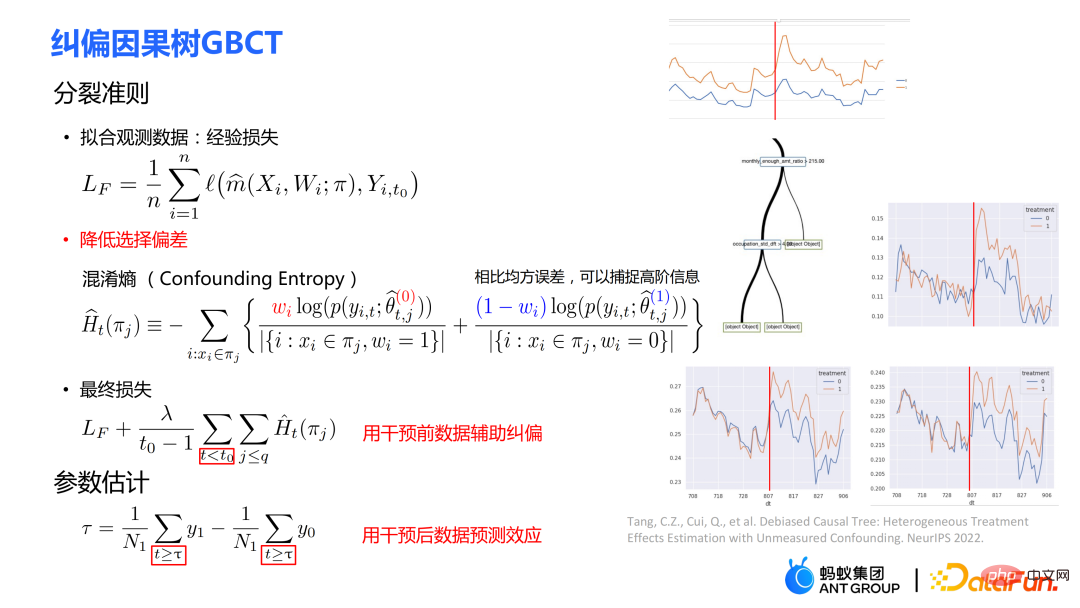
Pendekatan khusus:
① Kriteria pemisahan
- adalah serupa dengan pokok penyebab tradisional, yang mengurangkan kehilangan pengalaman dengan menyesuaikan hasil data sejarah. Contohnya, menyesuaikan tingkah laku pengguna melalui fungsi tanpa menyebut jumlahnya.
- Bahagian kedua kriteria pemisahan ialah menggunakan entropi kekeliruan. Berbanding dengan ralat kuasa dua min, entropi kekeliruan boleh menangkap maklumat peringkat lebih tinggi. Formula:
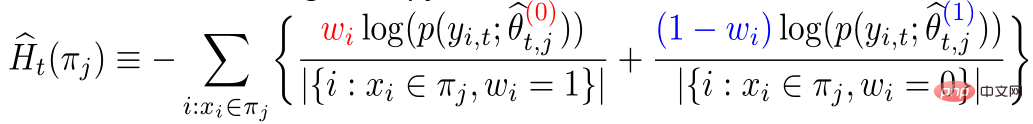
Maksud intuitif ialah: dalam kumpulan eksperimen, gunakan model kumpulan kawalan untuk anggaran; Dalam kumpulan kawalan, gunakan model kumpulan eksperimen untuk menganggarkan dua bahagian sedekat mungkin, supaya taburan kumpulan eksperimen dan kumpulan kawalan adalah hampir sama. Penggunaan entropi kekeliruan adalah salah satu sumbangan utama kerja kami.
- Kerugian akhir ialah jumlah wajaran dua bahagian di atas. Ambil perhatian bahawa penggunaan utama kehilangan adalah data sebelum intervensi (bahagian kehilangan pengalaman masih akan dipasang menggunakan data selepas intervensi), iaitu data sebelum campur tangan digunakan untuk pembetulan tambahan.
② Anggaran parameter
- Anggaran parameter menggunakan pasca intervensi (t≥τ ) data untuk menganggarkan kesan penyebab. Ia terutamanya menggunakan data sebelum campur tangan untuk membetulkan dan belajar untuk mendapatkan struktur pokok, dan menggunakan data selepas campur tangan dalam nod daun untuk menganggarkan kesan penyebab Memandangkan data sebelum campur tangan digunakan untuk pembetulan eksplisit, data selepas intervensi digunakan untuk mengira Anggaran akan lebih tepat.
- (sebelah kanan PPT) ditunjukkan dalam gambar di sebelah kanan. Garisan kuning mewakili kumpulan eksperimen dan kumpulan biru mewakili kumpulan kawalan. Sesetengah strategi dalam perniagaan mungkin menyebabkan peruntukan kumpulan eksperimen dan kumpulan kawalan menjadi tidak rawak, dan terdapat perbezaan yang ketara dalam pengagihan kedua-duanya. Selepas pembetulan GBCT, taburan data kumpulan eksperimen dan kumpulan kawalan sebelum intervensi pada nod daun pada asasnya diselaraskan, ia mencapai kesan yang serupa dengan eksperimen terkawal tersimulasi, data pasca intervensi adalah digunakan untuk menganggarkan kesan sebab (kawasan Huang di bawah garisan tolak kawasan di bawah garisan biru) adalah lebih tepat.
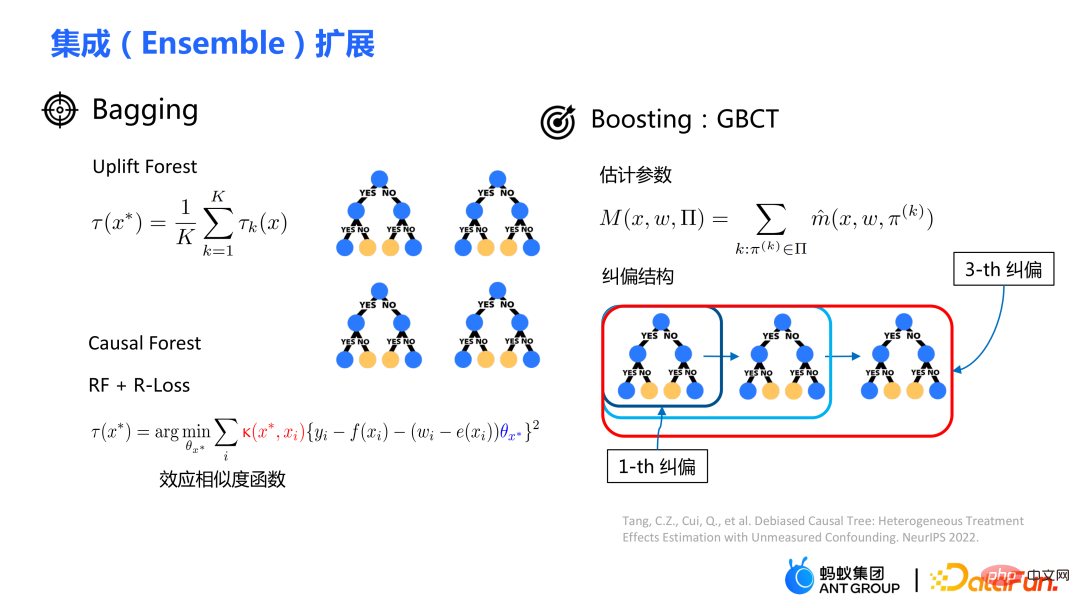
Penyepaduan model pokok tradisional termasuk kaedah seperti membungkus dan meningkatkan. Kaedah integrasi yang digunakan oleh hutan uplift atau hutan sebab ialah kaedah bagging Penyepaduan hutan uplift adalah penjumlahan langsung, manakala integrasi hutan penyebab memerlukan penyelesaian fungsi kerugian.
Disebabkan modul pembetulan eksplisit yang direka dalam GBCT, GBCT menyokong penggunaan kaedah penggalak untuk penyepaduan. Idea asas adalah serupa dengan boosting: selepas pokok pertama dibetulkan, pokok kedua dibetulkan, dan pokok ketiga dibetulkan...

Dua bahagian percubaan telah dilakukan:
① Percubaan simulasi. Di bawah eksperimen simulasi yang mengandungi kebenaran asas, uji sama ada kaedah GBCT boleh mencapai hasil yang diharapkan. Penjanaan data untuk eksperimen simulasi dibahagikan kepada dua bahagian (lajur pertama Φ dalam jadual mewakili bias pemilihan. Semakin besar nilai Φ, semakin kuat bias pemilihan yang sepadan; nilai dalam jadual ialah MAE. Semakin kecil nilai MAE , lebih baik kaedahnya) :
- Bahagian pertama ialah pembolehubah mengelirukan telah diperhatikan. Apabila semua pembolehubah yang mengelirukan diperhatikan, uji sama ada kaedah GBCT lebih teguh daripada kaedah tradisional. Dapat disimpulkan daripada data dalam jadual bahawa semakin besar bias pemilihan, semakin buruk prestasi kaedah tradisional (pembelajar meta, hutan sebab-akibat, dll.).
- Bahagian kedua ialah kewujudan pembolehubah mengelirukan yang tidak diperhatikan. Pada ketika ini, keberkesanan banyak kaedah tradisional akan menjadi lebih teruk. Bagi GBCT, prestasinya agak stabil dengan kehadiran pembolehubah yang tidak diperhatikan, dan prestasinya secara konsisten lebih baik daripada kaedah lain.
- Dua lajur terakhir (GBCT-ND, GBCT-B) dalam jadual ialah eksperimen ablasi, iaitu versi GBCT yang lemah dengan beberapa modul dialih keluar , yang menggambarkan lagi cadangan kami Setiap modul berguna.
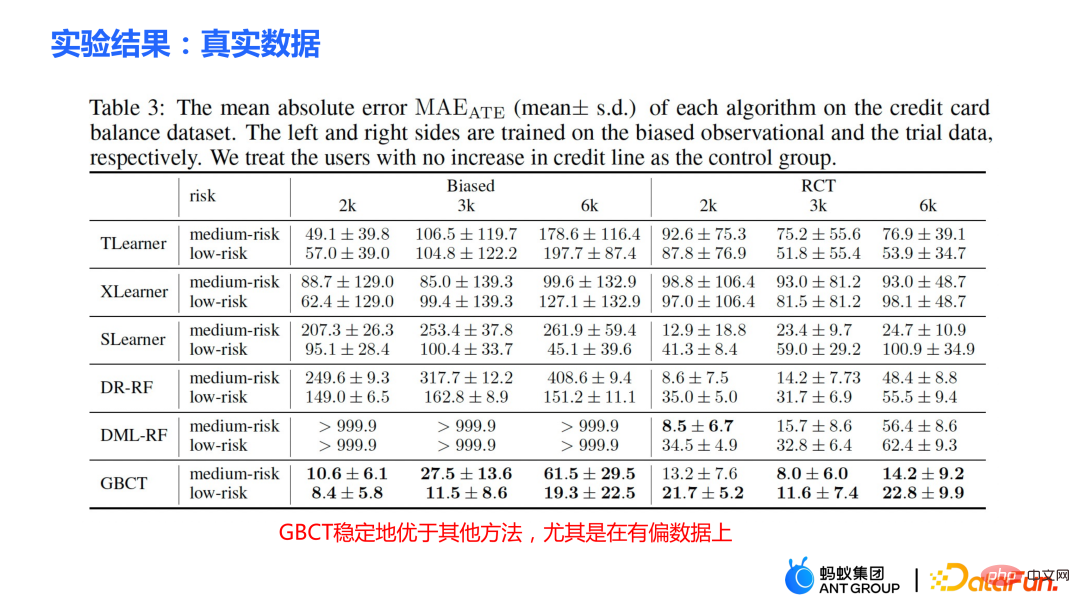
② Data peningkatan had kad kredit sebenar. Satu eksperimen terkawal rawak telah dijalankan, dan data berat sebelah telah dibina berdasarkan eksperimen terkawal rawak. Merentasi tetapan yang berbeza, kaedah GBCT secara konsisten mengatasi kaedah tradisional, terutamanya pada data berat sebelah, menunjukkan prestasi yang lebih baik daripada kaedah tradisional.
3. Gabungan data penyebab
Tugas kedua ialah gabungan data sebab, iaitu cara menganalisis data dengan lebih baik apabila terdapat pelbagai sumber data Menganggar sebab kesan.

Simbol utama: ialah pelbagai sumber data, Y ialah hasil, A ialah rawatan, X ialah persatuan kebimbangan Pembolehubah, Z ialah kovariat lain bagi setiap sumber data (domain) kecuali X, S ialah penunjuk domain untuk menunjukkan domain mana ia milik, dan μ ialah nilai jangkaan hasil yang berpotensi. Uraikan hasil ke dalam ungkapan berikut:
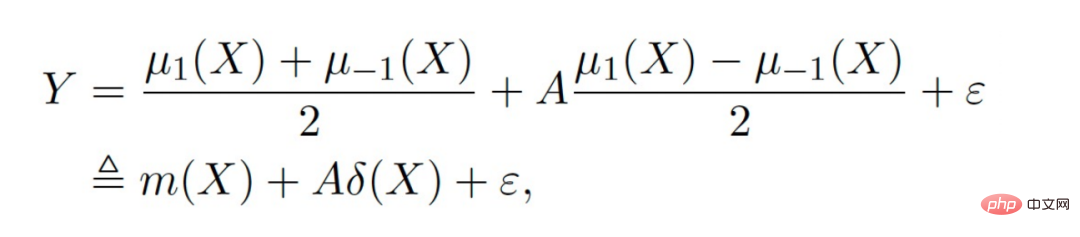
fungsi sasaran δ digunakan untuk menganggarkan kesan penyebab pada setiap domain, Dalam Selain itu, fungsi gangguan termasuk kesan utama, skor kecenderungan, skor kecenderungan domain, varians kesan, dsb.
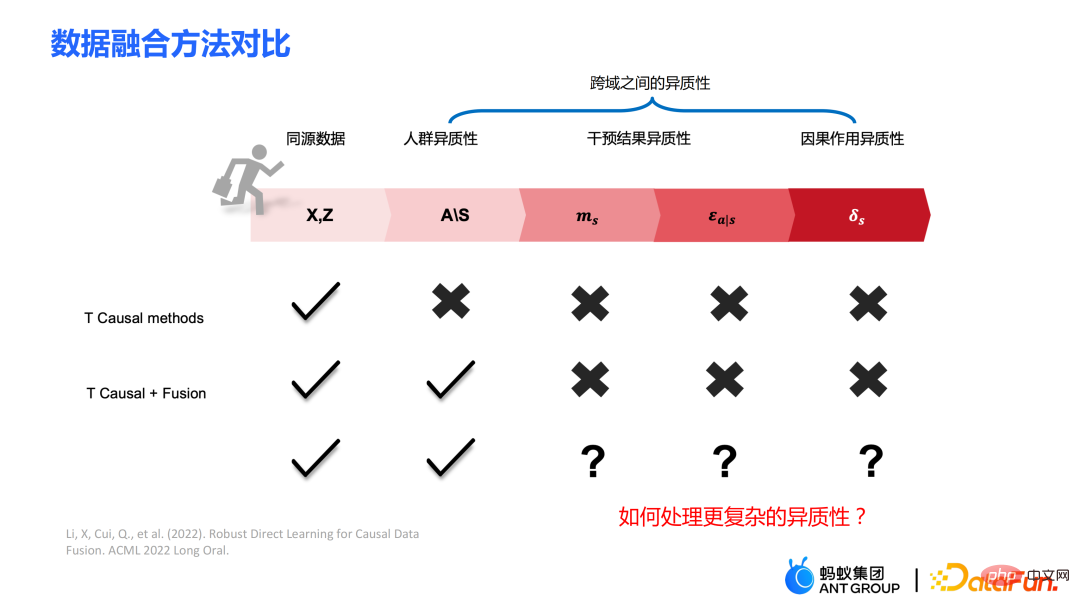
Sesetengah kaedah tradisional, seperti meta learner, menganggap bahawa data adalah homolog, iaitu pengedaran adalah konsisten . Sesetengah kaedah gabungan data tradisional boleh mengendalikan kepelbagaian populasi merentas domain, tetapi tidak dapat menangkap secara eksplisit kepelbagaian hasil intervensi dan kesan sebab akibat merentas domain. Kerja kami memberi tumpuan kepada menangani heterogeniti yang lebih kompleks merentas domain, termasuk heterogeniti merentas domain dalam hasil intervensi dan heterogeniti merentas domain dalam kesan sebab akibat.
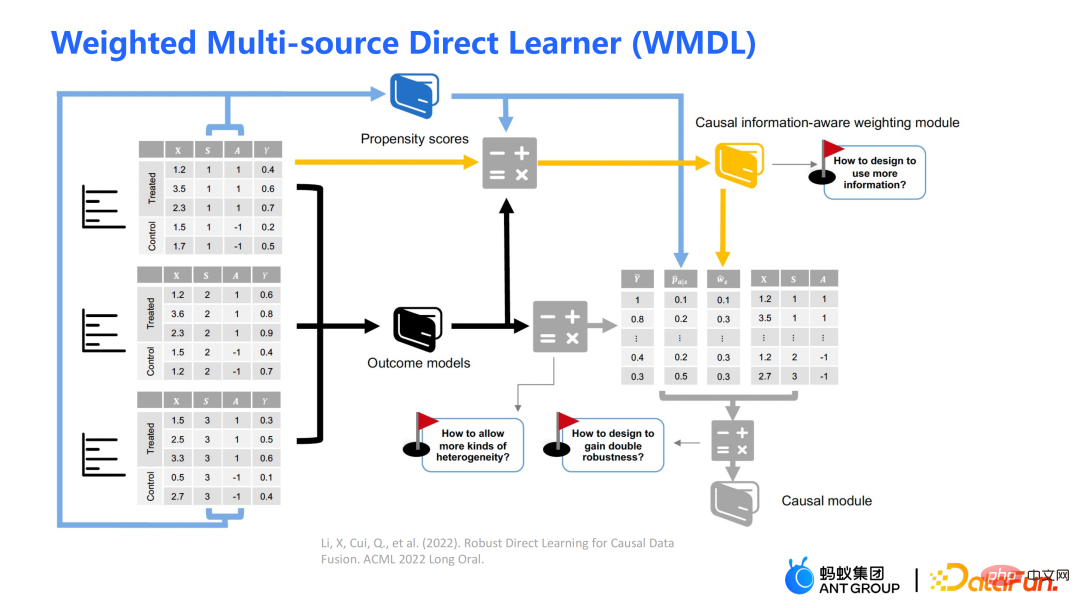
Rajah rangka kerja algoritma WMDL ditunjukkan dalam rajah di atas. Modul utama ialah:
- skor kecenderungan
- model hasil
- modul pemberat sedar maklumat sebab
Tiga modul digabungkan untuk mendapatkan anggaran akhir. Tiga sorotan algoritma WMDL ialah:
- Cara mencirikan darjah yang berbeza heterogen merentas domain
- Cara mereka bentuk modul pemberat untuk menggunakan maklumat lanjut
- Bagaimana untuk mendapatkan anggaran dua kali ganda yang mantap
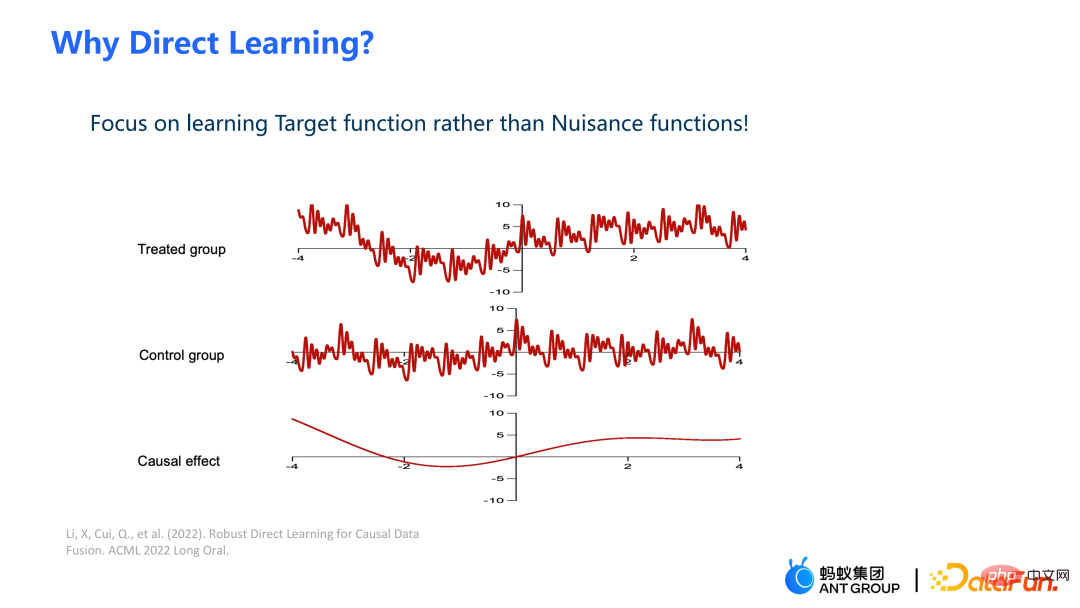
Dalam kerja ini, kami tidak menganggarkan hasil kumpulan eksperimen dan hasil kumpulan kawalan, dan kemudian membuat perbezaan untuk mendapatkan sebab dan akibat daripada menganggarkan kesan, kita menganggarkan secara langsung kesan sebab, iaitu Pembelajaran Langsung. Faedah Pembelajaran Langsung ialah ia boleh mengelakkan isyarat hingar frekuensi lebih tinggi dalam kumpulan eksperimen dan kawalan.

Bahagian kiri menganggap bahawa kesan sebab adalah sama antara berbilang domain, tetapi hasilnya mungkin heterogen ; bahagian kanan menganggap bahawa kesan sebab akibat antara setiap domain adalah berbeza, iaitu antara domain yang berbeza, walaupun kovariatnya adalah sama, kesan sebab akibatnya juga berbeza.
Formula diperoleh berdasarkan formula pembongkaran Hasil Y tolak kesan utama dibahagikan dengan rawatan dianggarkan sebagai I(X), dan penyelesaian optimum yang diperoleh ialah δ(X). Pengangka dalam  ialah modul pemberat yang sedar maklumat sebab yang akan disebut kemudian, yang merupakan sumbangan utama kerja kami; diambil kira. Jika kesan sebab akibat antara domain berbeza adalah berbeza, maklumat penunjuk domain juga akan dipertimbangkan.
ialah modul pemberat yang sedar maklumat sebab yang akan disebut kemudian, yang merupakan sumbangan utama kerja kami; diambil kira. Jika kesan sebab akibat antara domain berbeza adalah berbeza, maklumat penunjuk domain juga akan dipertimbangkan.
Kerja ini mempunyai tiga kelebihan:
① Melalui reka bentuk yang berbeza, ia bukan sahaja dapat mengendalikan kepelbagaian hasil intervensi, tetapi juga Mengendalikan heterogenitas antara kesan sebab;
② mempunyai sifat kekukuhan berganda. Buktinya diberikan dalam kertas bahawa selagi anggaran sama ada model skor kecenderungan domain atau model kesan utama tidak berat sebelah, anggaran akhir akan menjadi tidak berat sebelah (keadaan sebenar adalah lebih rumit sedikit, lihat kertas untuk butiran) ;
③ Kerja ini terutamanya mereka bentuk rangka kerja model separuh parametrik. Setiap modul model boleh menggunakan mana-mana model pembelajaran mesin, malah keseluruhan model boleh direka bentuk menjadi rangkaian saraf untuk mencapai pembelajaran hujung ke hujung.
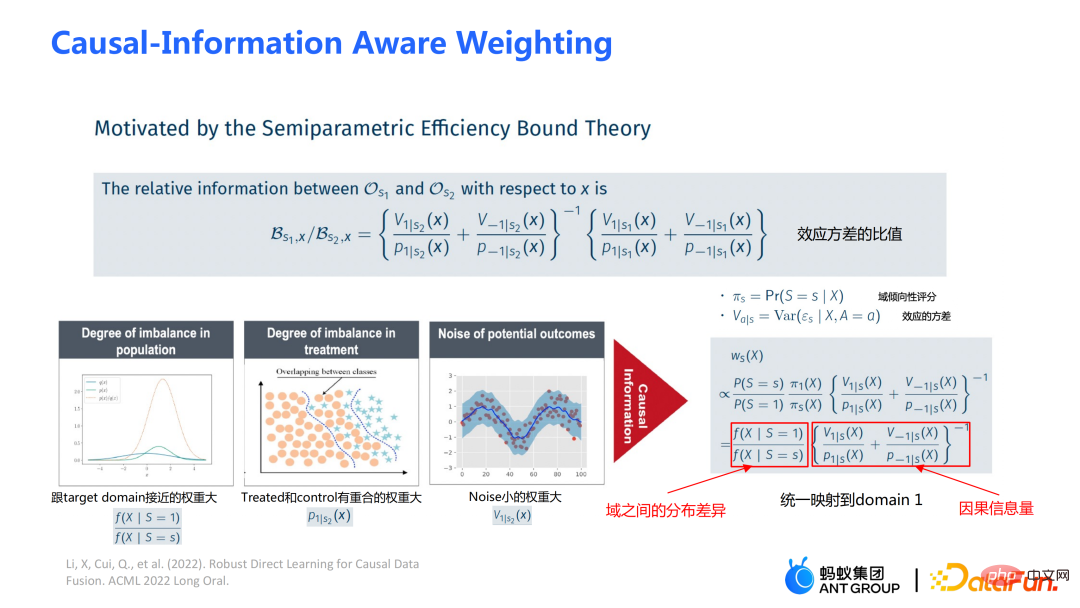
Modul pemberat diperoleh daripada teori terikat kecekapan dalam statistik. Ia terutamanya mengandungi dua aspek maklumat:
① 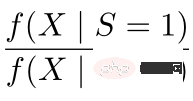 ialah modul untuk penukaran seimbang perbezaan pengedaran antara domain; >
ialah modul untuk penukaran seimbang perbezaan pengedaran antara domain; >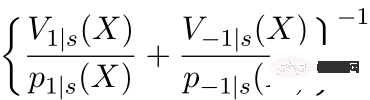 ialah modul maklumat kausal. Tiga gambar di sebelah kiri boleh digunakan untuk membantu pemahaman: Jika perbezaan taburan antara domain sumber dan domain sasaran adalah besar, keutamaan akan diberikan kepada sampel yang lebih dekat dengan domain sasaran
ialah modul maklumat kausal. Tiga gambar di sebelah kiri boleh digunakan untuk membantu pemahaman: Jika perbezaan taburan antara domain sumber dan domain sasaran adalah besar, keutamaan akan diberikan kepada sampel yang lebih dekat dengan domain sasaran
③ Gunakan V untuk mencirikan hingar dalam data. Oleh kerana hingar berada dalam penyebut, sampel yang kurang hingar akan mendapat pemberat yang lebih besar.
Dengan bijak menggabungkan tiga bahagian di atas, perbezaan taburan antara domain yang berbeza dan prestasi maklumat sebab yang berbeza boleh dipetakan ke dalam domain bersatu .

4. Aplikasi perniagaan dalam Ant
Dalam senario kawalan risiko kredit kewangan, kaedah intervensi seperti peningkatan kuota dan pengurangan harga dijangka mencapai kesan yang dijangkakan seperti perubahan dalam baki atau risiko. Dalam beberapa senario sebenar, kerja pembetulan GBCT akan menggunakan prestasi sejarah dalam tempoh sebelum angkat dahi (status kumpulan eksperimen dan kumpulan kawalan tanpa angkat dahi boleh diperolehi), dan menjalankan pembetulan eksplisit melalui maklumat sejarah, supaya intervensi nanti anggaran akan lebih tepat. Jika GBCT dibahagikan kepada nod kanak-kanak supaya tingkah laku sebelum intervensi diselaraskan, kesan sebab akibat selepas intervensi akan lebih mudah untuk dianggarkan. (Diperolehi selepas pembetulan) Dalam rajah, warna merah ialah kumpulan menaikkan dahi, warna biru ialah kumpulan tidak menaikkan dahi, dan kawasan kelabu di tengah adalah anggaran kesan penyebab. GBCT membantu kami membuat keputusan bijak yang lebih baik dan mengawal keseimbangan dan risiko produk kredit.
5 Sesi Soal Jawab
S1: Apakah persamaan dan perbezaan antara pembetulan GBCT dan kaedah perbezaan berganda (JPS). )?
A1: Idea utama pembetulan GBCT adalah menggunakan maklumat kawalan sejarah untuk mengurangkan kecenderungan pemilihan secara eksplisit Kaedah GBCT dan kaedah perbezaan berganda JPS mempunyai persamaan dan perbezaan :
- Persamaannya ialah kedua-duanya menggunakan maklumat sejarah; perbezaan terletak pada cara kedua-duanya memproses maklumat sejarah. JPS mengandaikan bahawa terdapat jurang malar tetap (jurang) antara kumpulan eksperimen dan kumpulan kawalan dalam data sejarah, dan menolak jurang (jurang) apabila meramal. Disebabkan bias pemilihan, peruntukan kumpulan eksperimen dan kumpulan kawalan adalah tidak rawak GBCT menjajarkan kumpulan eksperimen dan kumpulan kawalan sejarah melalui pembetulan bias.
- S2: GBCT akan berprestasi lebih baik pada pembolehubah mengelirukan yang tidak diperhatikan. Adakah terdapat penjelasan yang lebih intuitif?
A2: Jika semua pembolehubah yang mengelirukan telah diperhatikan, andaian ketidaktahuan adalah berpuas hati, sedikit sebanyak, walaupun bias pemilihan tidak dikurangkan secara eksplisit, eksperimen Ia juga mungkin untuk mencapai penjajaran antara kumpulan dan kumpulan kawalan melalui kaedah tradisional Eksperimen menunjukkan bahawa prestasi GBCT adalah lebih baik sedikit, dan hasilnya lebih stabil melalui pembetulan yang jelas.
Andaikan terdapat beberapa pembolehubah pengeliru yang tidak diperhatikan Senario jenis ini sangat biasa dalam amalan Terdapat juga pembolehubah yang tidak diperhatikan dalam data kawalan sejarah, seperti perubahan dalam keadaan keluarga dan pendapatan sebelum kuota dinaikkan, mungkin tidak dapat diperhatikan, tetapi tingkah laku kewangan pengguna telah ditunjukkan dalam data sejarah. Kami berharap dapat mengurangkan kecenderungan pemilihan secara eksplisit melalui kaedah seperti entropi kekeliruan melalui maklumat prestasi sejarah, supaya apabila pokok itu berpecah, kepelbagaian antara pembolehubah yang mengelirukan boleh dicirikan ke dalam nod anak berpecah. Di antara nod kanak-kanak, pembolehubah pengeliru yang tidak diperhatikan adalah agak hampir supaya ia mempunyai kebarangkalian yang lebih besar, jadi anggaran kesan sebab-akibat adalah secara relatif lebih tepat.
S3: Pernahkah anda membandingkan GBCT dengan Pembelajaran Mesin Berganda (DML)?
A3: Perbandingan telah dibuat. Pembelajaran Mesin Berganda ialah kaedah separuh parametrik. Kerja kami dalam artikel ini lebih menumpukan pada kaedah berasaskan pokok, jadi pelajar asas yang dipilih adalah kaedah berkaitan pokok atau hutan. DML-RF dalam jadual ialah versi Pembelajaran Mesin Berganda bagi Random Forest.
Berbanding dengan DML, GBCT terutamanya mempertimbangkan cara menggunakan data kawalan sejarah. Dalam kaedah perbandingan, hasil sejarah akan diproses secara langsung sebagai kovariat, tetapi kaedah pemprosesan ini jelas tidak menggunakan maklumat dengan baik.
S4: Masalah serupa yang mungkin dihadapi dalam perniagaan ialah mungkin terdapat kecenderungan pemilihan di luar talian. Walau bagaimanapun, berat sebelah dalam talian mungkin agak berbeza daripada berat sebelah luar talian. Pada masa ini, semasa melakukan penilaian kesan di luar talian, mungkin tiada cara untuk menganggarkan kesan luar talian dengan sangat tepat.
J4: Isu ini merupakan isu yang sangat penting dalam senario kewangan. Dalam promosi carian, perbezaan antara luar talian dan dalam talian boleh diatasi sebahagiannya melalui pembelajaran dalam talian atau ujian A/B. Dalam senario kewangan, bukan mudah untuk menjalankan eksperimen dalam talian kerana pengaruh dasar di samping itu, tempoh pemerhatian prestasi biasanya lebih lama Sebagai contoh, ia mengambil masa sekurang-kurangnya satu bulan untuk memerhati maklum balas pengguna untuk produk kredit. Oleh itu sebenarnya amat sukar untuk menyelesaikan masalah ini dengan sempurna.
Kami biasanya menggunakan kaedah berikut: gunakan data ujian tempoh berbeza (OOT) untuk pengesahan semasa penilaian luar talian untuk melihat keteguhan prestasinya. Jika prestasi ujian agak stabil, maka terdapat lebih banyak sebab untuk mempercayai bahawa prestasi dalam taliannya juga baik.
Atas ialah kandungan terperinci Bagaimana untuk menggunakan data dengan lebih baik dalam inferens sebab-akibat?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

