Rumah >Peranti teknologi >AI >Pasukan Makmal HCP Universiti Sun Yat-sen: Kejayaan baharu dalam penyelesaian masalah AI, rangkaian saraf membuka pintu kepada penaakulan matematik
Pasukan Makmal HCP Universiti Sun Yat-sen: Kejayaan baharu dalam penyelesaian masalah AI, rangkaian saraf membuka pintu kepada penaakulan matematik
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-09 22:11:251375semak imbas
Manusia perlu menguasai banyak mata pengetahuan untuk menyelesaikan sejumlah besar masalah matematik pada peringkat proses pertumbuhan mereka yang berbeza. Walau bagaimanapun, memahami titik pengetahuan tidak bermakna anda benar-benar memahaminya Hanya dengan dapat menyelesaikan masalah anda dapat mencerminkan kebijaksanaan manusia. Dalam tahun-tahun kebelakangan ini, rangkaian saraf telah mencapai kejayaan besar dalam bidang penglihatan komputer, padanan corak, pemprosesan bahasa semula jadi, pembelajaran pengukuhan, dll. Walau bagaimanapun, keupayaan penaakulan gabungan diskret model rangkaian saraf jauh lebih rendah daripada manusia. Jadi, bolehkah rangkaian saraf memahami masalah matematik dan menyelesaikannya? Jika ya, sejauh manakah keupayaan menyelesaikan masalah rangkaian saraf?
Dari segi bentuk data, masalah matematik boleh dianggap sebagai urutan, dan penyelesaiannya (langkah penyelesaian masalah atau ungkapan) sering dibentangkan dalam bentuk urutan. Kemudian menyelesaikan masalah matematik boleh dianggap sebagai masalah terjemahan daripada bahasa semula jadi kepada bahasa matematik Model rangkaian saraf secara formal boleh menyelesaikan masalah matematik. Dapat diketahui daripada pelbagai kerja penyelidikan terdahulu bahawa rangkaian saraf boleh mencapai prestasi yang sangat baik pada masalah terjemahan dan telah mengatasi prestasi manusia pada beberapa set data. Walau bagaimanapun, ia jauh berbeza daripada terjemahan mesin Selain keupayaan untuk memahami semantik soalan, menyelesaikan masalah matematik selalunya memerlukan model untuk mempunyai keupayaan untuk menaakul tentang gabungan diskret objek dan entiti umum algebra.
Untuk meneroka keupayaan model mendalam untuk menyelesaikan masalah matematik, Makmal Integrasi Kecerdasan Manusia-Mesin Universiti Sun Yat-sen menggunakan masalah aplikasi matematik dan masalah pengiraan geometri di sekolah rendah dan menengah berdasarkan penyelidikan terdahulu. Untuk memulakan, satu siri kajian telah dijalankan untuk meningkatkan pemahaman semantik, penaakulan kognitif dan keupayaan penyelesaian masalah matematik model mendalam. Artikel ini akan memperkenalkan secara ringkas satu siri penyelidikan dalam bidang penyelesaian masalah matematik oleh Makmal Integrasi Pintar Manusia-Mesin-Objek Universiti Sun Yat-sen.
Kertas 1: Penyelesai Berstruktur Pokok Universal Penjajaran Semantik untuk Masalah Perkataan Matematik

Persidangan 2020 mengenai Kaedah Empirikal dalam Pemprosesan Bahasa Semulajadi
Alamat kertas: https://aclanthology. org/2020.emnlp-main.309.pdf
Penyelesaikan masalah perkataan matematik yang praktikal seharusnya dapat menyelesaikan pelbagai jenis masalah perkataan matematik, seperti persamaan linear satu pembolehubah, Sistem persamaan linear dua pembolehubah, persamaan kuadratik satu pembolehubah, dsb. Walau bagaimanapun, kebanyakan kerja penyelesaian masalah aplikasi matematik hanya direka untuk empat operasi aritmetik, dan reka bentuk jenis ini selalunya sukar untuk dikembangkan kepada lebih banyak jenis masalah. Adalah mustahil untuk menggunakan penyelesai masalah aplikasi matematik bersatu untuk menyelesaikan pelbagai jenis ungkapan di soalan aplikasi pada masa yang sama. Di samping itu, kebanyakan penyelesai masalah perkataan matematik semasa tidak mempunyai kekangan semantik antara teks masalah dan ungkapan penyelesaian.
Sebagai tindak balas kepada masalah di atas, pasukan Makmal Integrasi Perisikan Manusia-Mesin Universiti Sun Yat-sen mencadangkan skema perwakilan pokok ekspresi bersatu Dengan memperkenalkan pengendali tambahan untuk menyambungkan berbilang ungkapan, satu -yuan Ungkapan persamaan linear, persamaan linear dua pembolehubah, persamaan kuadratik satu pembolehubah dan jenis ungkapan lain boleh dinyatakan dalam cara yang bersatu, yang boleh memudahkan reka bentuk penyelesai dan menyelesaikan pelbagai jenis masalah aplikasi, seperti yang ditunjukkan dalam Rajah 1.
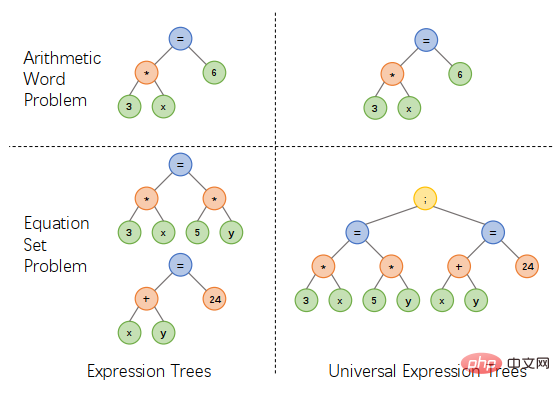
Rajah 1 Reka bentuk perwakilan pokok ungkapan bersatu
Berdasarkan skema perwakilan pokok ungkapan bersatu, kami selanjutnya mencadangkan penyelesai sejagat struktur pokok semantik (SAU-Solver), seperti ditunjukkan dalam Rajah 2. Penyelesai universal berstruktur pokok kami terdiri daripada dua bahagian, pengekod masalah berdasarkan GRU dua lapisan dan penyahkod berstruktur pokok berdasarkan perwakilan pokok ungkapan bersatu. Dan semasa proses latihan, kami memperkenalkan penyelarasan penjajaran semantik Dengan mengekang ketekalan subpokok ungkapan dan konteks soalan, penyelesai umum kami boleh mempertimbangkan hubungan semantik antara masalah dan ungkapan, dan meneroka pelbagai jenis masalah pengetahuan, dengan itu meningkatkan keupayaan penjanaan ekspresi penyelesai.
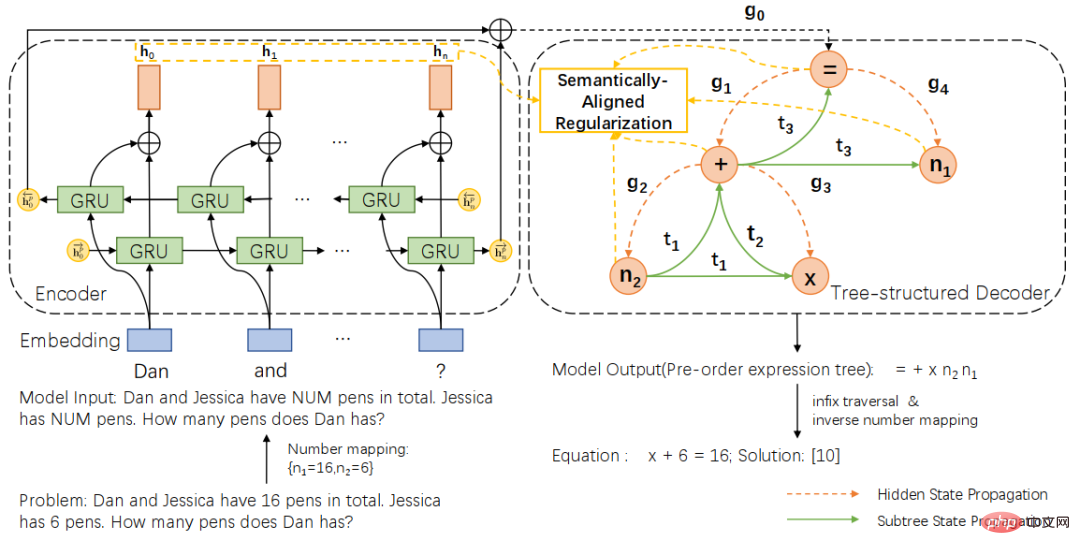
Rajah 2 Penyelesai struktur pokok penjajaran semantik
Selain itu, untuk mengukur fleksibiliti dan keupayaan penyelesaian dengan lebih baik bagi penyelesai, kami juga membina set data berbilang soalan bersaiz sederhana HMWP untuk masalah dengan satu jenis soalan dalam set data anotasi semasa Set data termasuk beribu-ribu soalan teks matematik yang menyelesaikan pelbagai jenis ungkapan seperti persamaan linear satu pembolehubah, sistem persamaan linear dua pembolehubah, persamaan kuadratik satu pembolehubah, dsb. Percubaan kami menunjukkan bahawa set data dengan pelbagai jenis soalan adalah lebih mencabar untuk penyelesai berbanding set data dengan satu jenis. Set data juga boleh mengukur keupayaan menyelesaikan masalah dengan lebih baik dan mempromosikan penyelidikan dalam komuniti penyelesai.
Dalam percubaan, artikel tersebut membandingkan SAU-Solver yang dicadangkan dengan kaedah sedia ada pada HMWP, Math23K, ALG514 dan Dolphin18K-Manual. Keputusan eksperimen ditunjukkan dalam rajah di bawah, yang membuktikan kepelbagaian dan keupayaan penyelesaian masalah matematik yang lebih baik bagi kaedah kami.
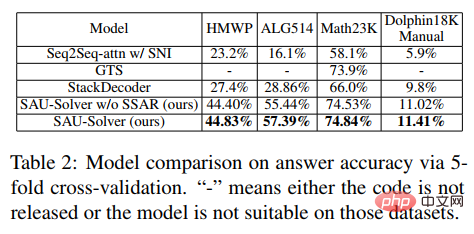
Untuk butiran penyelidikan lanjut, sila rujuk kertas asal.
Kertas 2: Penyelesai Neural-Simbolik untuk Masalah Perkataan Matematik dengan Tugasan Bantu

Mesyuarat Tahunan ke-59 Persatuan Linguistik Pengiraan dan Persidangan Bersama Antarabangsa ke-11 mengenai Pemprosesan Bahasa Semulajadi
Alamat kertas: https://arxiv.org/abs/2107.01431
Penyelesai masalah perkataan matematik asas semasa tidak mempertimbangkan pelbagai kekangan simbol matematik, tetapi hanya mudah Masalahnya ialah diselesaikan menggunakan rangka kerja penyahkod pengekod secara tidak betul, mengakibatkan ramalan yang tidak munasabah. Pengenalan kekangan simbolik dan penaakulan simbolik adalah sangat kritikal untuk menyelesaikan masalah aplikasi matematik secara automatik.
Oleh itu, pasukan Makmal Integrasi Perisikan Manusia-Mesin Universiti Sun Yat-sen memperkenalkan paradigma pengkomputeran neuro-simbolik dan mencadangkan penyelesai simbol-neural (NS-Solver) baharu untuk membantu dalam tugas Lakukan suntikan pengetahuan eksplisit untuk mencapai tahap kekangan simbolik yang berbeza. Seni bina teknikalnya ditunjukkan dalam Rajah 3. NS-Solver dibina di atas tulang belakang rangkaian oleh tiga komponen: 1) Pembaca Masalah, yang melaksanakan pemahaman semantik yang cekap dan perwakilan masalah matematik melalui rangkaian GRU dua hala 2) Pengaturcara, yang bertanggungjawab untuk penaakulan simbolik; pada semantik masalah dan keputusan ramalan akal , menjana ungkapan penyelesaian. 3) Pelaksana, menggunakan perpustakaan sympy untuk menyelesaikan ungkapan dan mendapatkan jawapan akhir.
Dari segi kekangan simbol, kami mencadangkan pelbagai tugas tambahan untuk menggunakan isyarat latihan tambahan dan hasil ramalan akal untuk mengekang jadual simbol secara eksplisit dan mengurangkan ruang carian penyelesaian masalah: 1 ) Tugas ramalan nombor diselia sendiri: lebih memahami semantik soalan dengan meramalkan kedudukan dan bilangan nombor dalam soalan 2) Tugas ramalan pengkuantiti akal: menyuntik pengetahuan akal dan menggunakan hasil ramalan untuk mengekang jadual simbol dan mengurangkan ruang carian; 3) Semakan Konsistensi: Semak ketekalan antara output penyelesai dan ungkapan sasaran dari tahap semantik 4) Tugas penggunaan dua kali: Menguatkan pemahaman semantik masalah melalui kekangan dua hala daripada masalah; kepada luahan dan luahan kepada masalah.
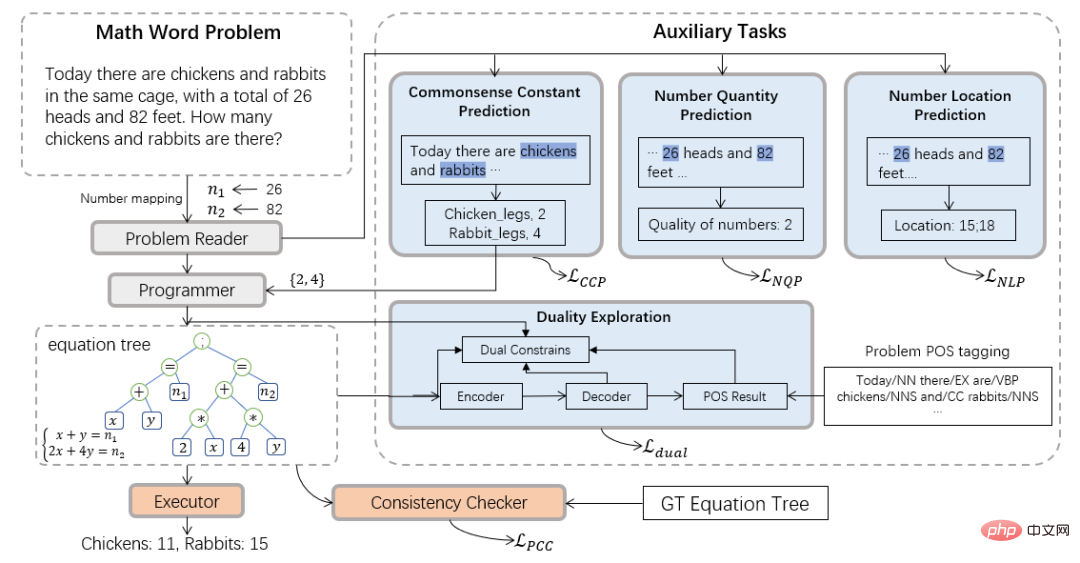
Rajah 3 Neural-Simbolic Solver (NS-Solver)
Selain itu, untuk mengesahkan prestasi penyelesai dengan lebih baik, kami juga membina set data masalah aplikasi matematik berbilang soalan yang lebih besar CM17K untuk mempromosikan penyelidikan dengan lebih baik dalam komuniti penyelesaian masalah matematik. CM17K mengandungi 6215 masalah aritmetik empat pembolehubah, 5193 persamaan linear satu pembolehubah, 3129 persamaan tak linear bagi satu pembolehubah dan 2498 masalah persamaan. Statistik data CM17K dan Math23K ditunjukkan dalam jadual di bawah. Ia boleh dilihat daripada statistik bahawa CM17K mempunyai maklumat soalan yang lebih panjang, ungkapan penyelesaian yang lebih panjang, dan melibatkan lebih akal daripada Math23K, yang bermaksud CM17K mencirikan prestasi penyelesai masalah dengan lebih baik dari segi kesukaran menyelesaikan.
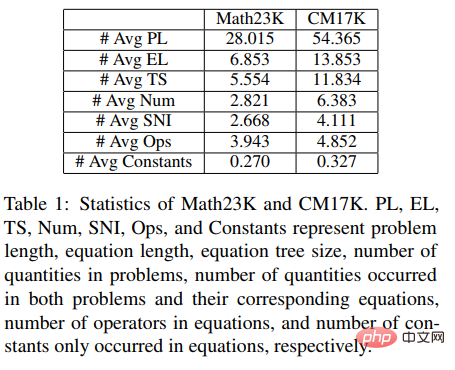
Dalam eksperimen, artikel membandingkan cadangan NS-Solver dengan kaedah sedia ada pada Math23K dan CM17K, dan menjalankan eksperimen ablasi untuk membuktikan bahawa NS-Solver Kemahiran menyelesaikan masalah yang baik dan serba boleh. Keputusan eksperimen ditunjukkan dalam dua jadual berikut.
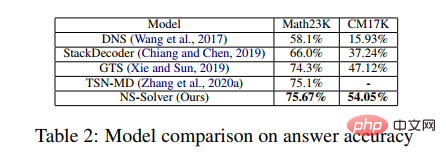
Selain itu, kami juga menjalankan eksperimen ablasi pada tugas tambahan, seperti yang ditunjukkan dalam rajah di bawah. Keputusan eksperimen membuktikan bahawa setiap tugas tambahan boleh meningkatkan keupayaan penyelesaian masalah NS-Solver.
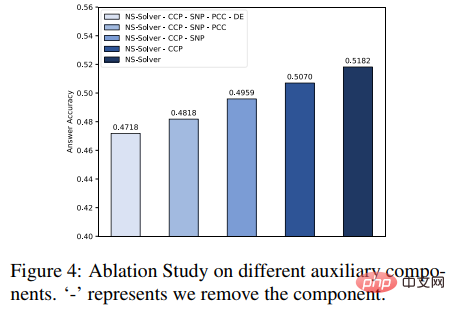
Untuk butiran penyelidikan lanjut, sila rujuk kertas asal.
Kertas 3: GeoQA – Penanda Aras Menjawab Soalan Geometri ke arah Penaakulan Berangka Berbilang Modal

Penemuan Persatuan Linguistik Pengiraan: ACL-IJCNLP 2021
Alamat kertas: https://arxiv .org/pdf/2105.14517.pdf
Penyelesaian masalah matematik automatik semakin mendapat perhatian baru-baru ini. Penyelesaian Masalah Matematik Automatik Kebanyakan kerja tertumpu pada penyelesaian automatik masalah perkataan matematik. Walau bagaimanapun, beberapa kerja memberi tumpuan kepada masalah geometri. Berbanding dengan soalan aplikasi matematik, soalan geometri memerlukan pemahaman huraian teks dan grafik dan carta pada masa yang sama, kerana dalam soalan geometri, teks soalan dan grafik dan carta biasanya saling melengkapi dan amat diperlukan. Kaedah sedia ada untuk menyelesaikan masalah geometri secara automatik sangat bergantung pada peraturan dan hanya dinilai pada set data yang kecil.

Rajah 4 Contoh Soalan Geometri
Untuk mempromosikan penyelidikan mengenai penyelesaian automatik masalah geometri, pasukan Makmal Integrasi Kecerdasan Manusia-Mesin Universiti Sun Yat-sen telah membina set data soalan dan jawapan GeoQA yang terdiri daripada 5010 soalan aneka pilihan geometri. Seperti yang ditunjukkan dalam Rajah 4, setiap sampel dalam set data GeoQA mempunyai huraian soalan, imej geometri, pilihan soalan, jawapan, jenis soalan, mata pengetahuan, analisis penyelesaian, dan prosedur formal yang ditandakan dengan langkah penyelesaian masalah. Dari segi saiz masalah, set data ini adalah 25 kali lebih besar daripada set data GeoS yang biasa digunakan dalam kerja sebelumnya. Maklumat statistik berkaitan set data GeoQA ditunjukkan dalam jadual di bawah.
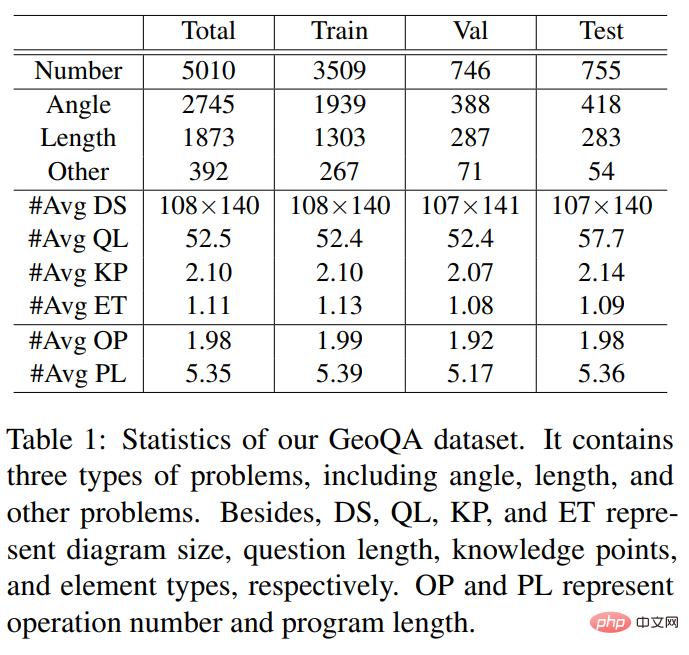
Pengendali program formal dan pemalar yang terlibat digunakan oleh dataset GeoQA ditunjukkan dalam jadual di bawah.

Untuk menggalakkan penyelidikan penyelesai masalah geometri dengan lebih baik, selain membina beberapa model garis dasar berdasarkan set data GeoQA, kami juga Penyelesai masalah neurogeometrik NGS dicadangkan untuk memahami maklumat semantik pelbagai mod dan menjana program formal yang boleh ditafsir. Reka bentuk keseluruhan NGS penyelesai masalah neurogeometrik ditunjukkan dalam Rajah 5.
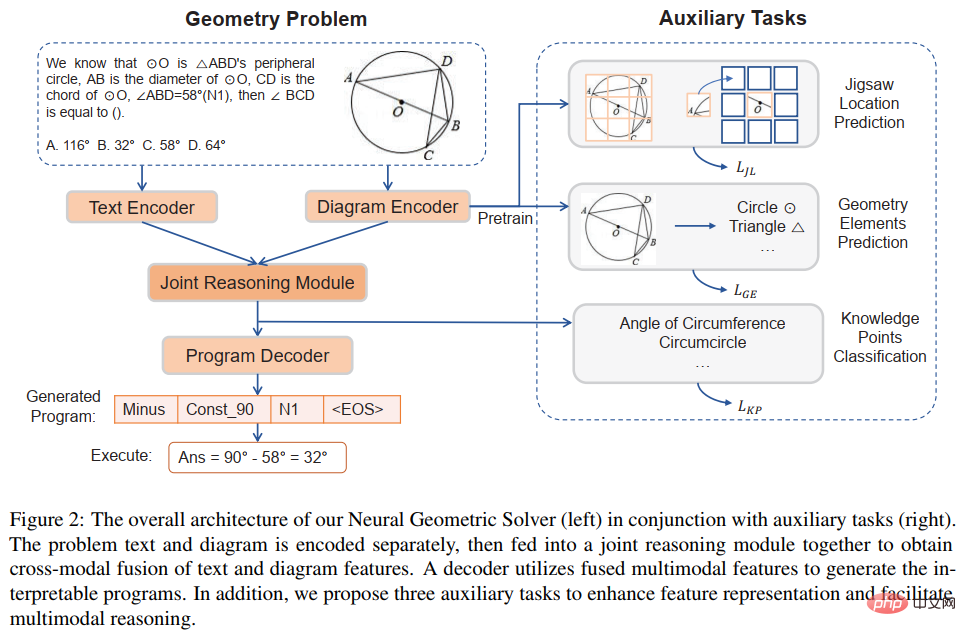
Rajah 5 Gambarajah skematik penyelesai masalah geometri saraf (NGS)
NGS kami terutamanya terdiri daripada pengekod teks, pengekod geometri, modul inferens bersama dan penyahkod atur cara. Pengekod teks bertanggungjawab untuk perwakilan semantik teks soalan, dan pengekod angka geometri bertanggungjawab untuk perwakilan angka geometri. Kedua-dua perwakilan teks dan perwakilan grafik akan menjadi input kepada model penaakulan bersama untuk perwakilan semantik berbilang modal, dan disalurkan kepada penyahkod atur cara untuk penyahkodan atur cara, dan program penyelesaian formal yang boleh ditafsir dan boleh dilaksanakan akan dikeluarkan.
Di samping itu, untuk meningkatkan keupayaan perwakilan angka geometri oleh pengekod angka geometri dan mempromosikan modul penaakulan bersama untuk menyepadukan sepenuhnya dan menyatakan maklumat pelbagai mod yang terkandung dalam soalan, kami juga memperkenalkan Pelbagai tugas tambahan dilaksanakan untuk meningkatkan keupayaan perwakilan model dan menyuntik pengetahuan teorem. Tugas tambahan ini termasuk: 1) Ramalan kedudukan teka-teki: pemahaman grafik aras piksel bagi rajah geometri dicapai dengan memotong rajah geometri kepada berbilang tampalan, menyusunnya secara rawak, dan kemudian membiarkan pengekod geometri menyusunnya semula 2) Ramalan unsur geometri: Biar pengekod rajah geometri belajar untuk meramalkan unsur geometri yang muncul dalam rajah geometri semasa untuk mencapai pemahaman grafik peringkat objek 3) Ramalan titik pengetahuan: melakukan gabungan pelbagai mod bagi perwakilan teks soalan dan perwakilan rajah geometri dalam modul penaakulan bersama; pada masa yang sama, tugas pengelasan mata pengetahuan diperkenalkan untuk menambah baik perwakilan masalah keseluruhan. Dalam NGS, kami melatih pengekod geometri menggunakan ramalan kedudukan teka-teki dan ramalan unsur geometri. Tugas ramalan titik pengetahuan digunakan sebagai subtugas untuk latihan pelbagai tugas dengan NGS.
Dalam percubaan, artikel itu membina berbilang model garis dasar berasaskan rangkaian saraf berdasarkan GeoQA dan membandingkan NGS dengannya. Keputusan eksperimen NGS dan model garis dasar pada GeoQA ditunjukkan dalam jadual di bawah.
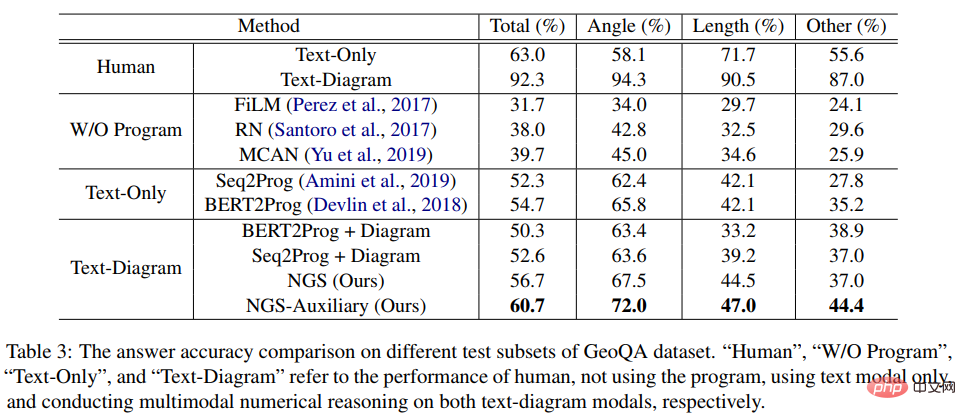
Seperti yang dapat dilihat daripada jadual di atas, NGS boleh mencapai prestasi penyelesaian masalah yang lebih baik pada GeoQA berbanding model garis dasar. Walau bagaimanapun, kita juga dapat melihat bahawa masih terdapat jurang yang besar antara pelbagai model dan manusia dalam menyelesaikan masalah geometri.
Selain itu, kami menjalankan pelbagai eksperimen ablasi untuk mengesahkan keberkesanan pelbagai reka bentuk dalam NGS. Untuk butiran penyelidikan lanjut, sila rujuk kertas asal.
Kertas 4: Penanda Aras Masalah Perkataan Matematik Tidak Bincang untuk Mengurangkan Bias Penyelesaian

Penemuan Persatuan Linguistik Pengiraan: NAACL 2022
Alamat kertas: https://aclanthology.org/2022 .findings-naacl.104.pdf
Dalam kerja ini, pasukan Makmal Integrasi Perisikan Manusia-Mesin Universiti Sun Yat-sen meneliti semula penilaian pada penanda aras semasa untuk menyelesaikan masalah aplikasi matematik Kecondongan penyelesaian model. Kecondongan penyelesaian masalah ini disebabkan terutamanya oleh bias data dan kecenderungan pembelajaran. Bias data merujuk kepada masalah bahawa set data latihan gagal merangkumi semua kaedah naratif yang berbeza bagi setiap soalan Akibatnya, model penyelesaian masalah hanya boleh mempelajari semantik cetek dan gagal memahami semantik yang mendalam bagi maksud soalan, seperti. Seperti yang ditunjukkan dalam Rajah 6(a), memandangkan model penyelesaian masalah hanya mempelajari semantik cetek dan menggunakannya untuk menyelesaikan masalah, walaupun selepas kita mengalih keluar bahagian masalah masalah, penyelesai masalah masih boleh mencapai 69.4%.
Bidang pembelajaran bermakna MWP boleh diselesaikan dengan berbilang ungkapan setara, tetapi set data semasa hanya menggunakan salah satu persamaan yang setara sebagai label Memaksa model untuk mempelajari label ini manakala mengabaikan persamaan setara yang lain membawa kepada berat sebelah dalam latihan pembelajaran. Seperti yang ditunjukkan dalam Rajah 6(b), semasa proses latihan, model mungkin menghasilkan ungkapan yang tidak konsisten dengan ungkapan GroundTruth tetapi jawapannya betul Namun, kerana set data hanya menggunakan ungkapan setara tertentu sebagai label, ia akan membawa kepada Apabila mengira fungsi kehilangan, ungkapan itu dianggap sebagai ungkapan yang salah, dan kehilangan antara dua ungkapan yang betul disebarkan kembali kepada model penyelesaian, mengakibatkan pembetulan berlebihan model.

Rajah 6 Contoh bias data dan bias pembelajaran
Untuk mengurangkan bias data, pasukan Makmal Integrasi Kecerdasan Manusia-Mesin Universiti Sun Yat-sen membuat percubaan baharu Kami melabelkan semula MWP baharu dengan cara yang merangkumi soalan soalan sebanyak mungkin . Penanda Aras MWP. Kami mengumpul 2907 masalah perkataan sebagai soalan asas, dan kemudian kami menjelaskan seberapa banyak soalan yang mungkin untuk cerita yang terkandung dalam setiap soalan.
Untuk memudahkan proses anotasi manual, kami mula-mula menjana beberapa ungkapan yang munasabah berdasarkan kandungan tulang belakang soalan, dan kemudian menulis semula soalan secara terbalik. Untuk menjana ungkapan yang munasabah, kami mereka bentuk tiga varian ungkapan: 1) Varian pelbagai pembolehubah (Va): pilih secara rawak dua pembolehubah berangka daripada tulang belakang soalan dan gunakan operator matematik (+, -, *, /) Gabungkan mereka, seperti sebagai n0 + n1, n0 − n1, dsb. 2) Transformasi subungkapan (Sub): Semua subungkapan yang terkandung dalam ungkapan sasaran soalan asal diubah suai oleh pengendali, dengan itu memperoleh ungkapan baharu. 3) Ubah bentuk Ungkapan Keseluruhan (Whole): dapatkan ungkapan baharu dengan menukar operator yang terkandung dalam ungkapan sasaran soalan asal. Set ungkapan baharu yang diperoleh daripada tiga varian di atas ditapis secara manual, ungkapan yang tidak boleh dianotasi dengan soalan baharu ditapis keluar dan ungkapan yang selebihnya dianotasi secara manual dengan soalan.
Untuk mengurangkan berat sebelah pembelajaran, kami mencadangkan strategi pemilihan sasaran dinamik Semasa proses latihan, berdasarkan hasil output model, ekspresi sasaran yang lebih dekat dengannya dipilih sebagai GroundTruth. Untuk mendapatkan ungkapan yang setara, kami menggunakan hukum komutatif dalam operasi matematik untuk mengubah bentuk pokok ungkapan untuk mendapatkan berbilang ungkapan setara. Seperti yang ditunjukkan dalam Rajah 7.
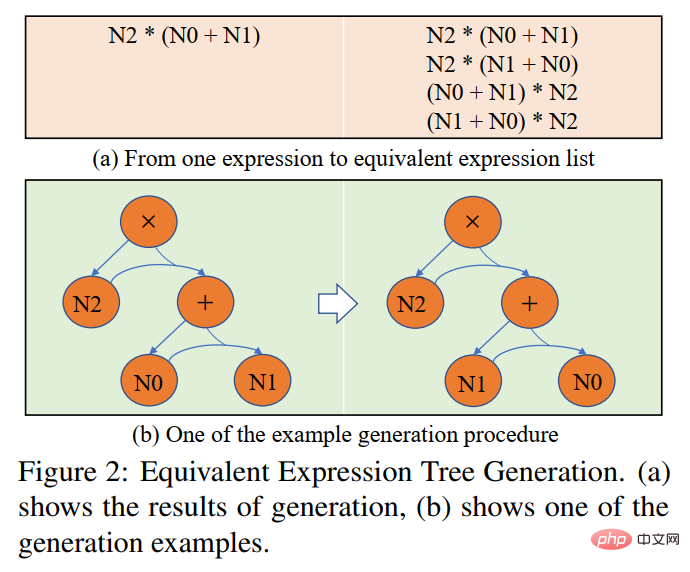
Rajah 7 Gambarajah skematik penjanaan pokok ungkapan setara
Dalam percubaan, artikel itu mula-mula mengesahkan set data UnbiasedMWP pada berbilang model garis dasar SOTA. Keputusan eksperimen ditunjukkan dalam jadual di bawah.
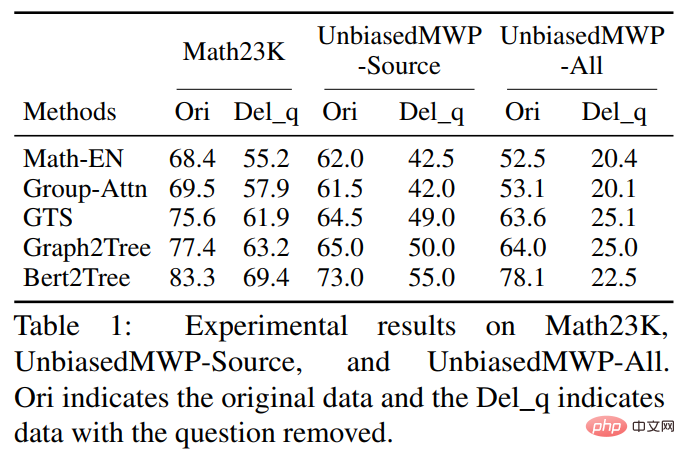
Daripada keputusan eksperimen, kita dapat melihat bahawa berbanding dengan Math23K sedia ada, set data kami UnbiasedMWP mempunyai kurang bias data kerana Apabila kami mengalih keluar soalan , prestasi penyelesaian model menurun secara mendadak, yang membuktikan bahawa set data kami menjadikan model perlu memberi perhatian kepada maklumat semantik yang mendalam untuk menyelesaikan masalah.
Untuk mengesahkan sama ada strategi pemilihan sasaran dinamik kami boleh mengurangkan berat sebelah pembelajaran, kami menggunakan strategi pemilihan sasaran dinamik pada berbilang model penyelesaian masalah. Keputusan eksperimen ditunjukkan dalam jadual di bawah.
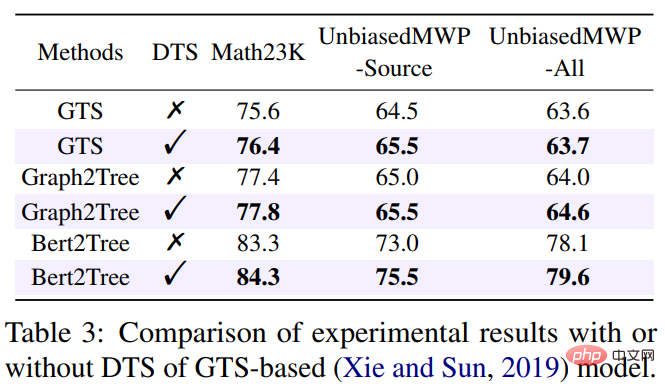
Daripada keputusan percubaan, kami dapat melihat bahawa strategi pemilihan sasaran dinamik kami dapat mengurangkan berat sebelah pembelajaran secara berkesan dan meningkatkan kesan penyelesaian model. Untuk butiran penyelidikan lanjut, sila rujuk kertas asal.
Kertas 5: Penyelesaian Logik: Ke Arah Penyelesaian Masalah Perkataan Matematik yang Boleh Ditafsir dengan Pembelajaran Dipertingkatkan Sejurus Logik

Penemuan Persatuan Linguistik Pengiraan: EMNLP 2022
Alamat kertas: https:// arxiv.org/pdf/2205.08232.pdf
Dalam beberapa tahun kebelakangan ini, model pembelajaran mendalam telah mencapai kejayaan besar dalam menyelesaikan masalah aplikasi matematik secara automatik, terutamanya dalam menyediakan jawapan yang tepat. Walau bagaimanapun, kerana model ini hanya menggunakan petunjuk statistik (heuristik cetek) untuk mencapai prestasi penyelesaian yang tinggi dan tidak benar-benar memahami dan menaakul tentang logik matematik di sebalik masalah, kaedah ini sukar untuk dijelaskan.
Untuk menyelesaikan masalah ini dan menggalakkan pembangunan bidang penyelesaian masalah perkataan matematik yang boleh ditafsir, pasukan Makmal Integrasi Kecerdasan Manusia-Mesin Universiti Sun Yat-sen telah membina data masalah perkataan matematik yang dijelaskan berkualiti tinggi yang pertama. ditetapkan, InterMWP. Set data ini mengandungi 11,495 masalah perkataan matematik dan 210 formula logik berdasarkan pengetahuan algebra. Berbeza daripada set data penyelesaian masalah aplikasi matematik sedia ada, InterMWP kami bukan sahaja memerlukan penyelesai untuk mengeluarkan ungkapan penyelesaian, tetapi juga memerlukan penyelesai masalah untuk mengeluarkan ungkapan logik berdasarkan pengetahuan algebra yang sepadan dengan ungkapan penyelesaian, dengan itu merealisasikan model Penjelasan tentang keluarannya. Persamaan dan perbezaan antara set data InterMWP dan set data penyelesaian masalah lain boleh dilihat dalam Rajah 8. Untuk proses anotasi khusus, sila rujuk teks asal.
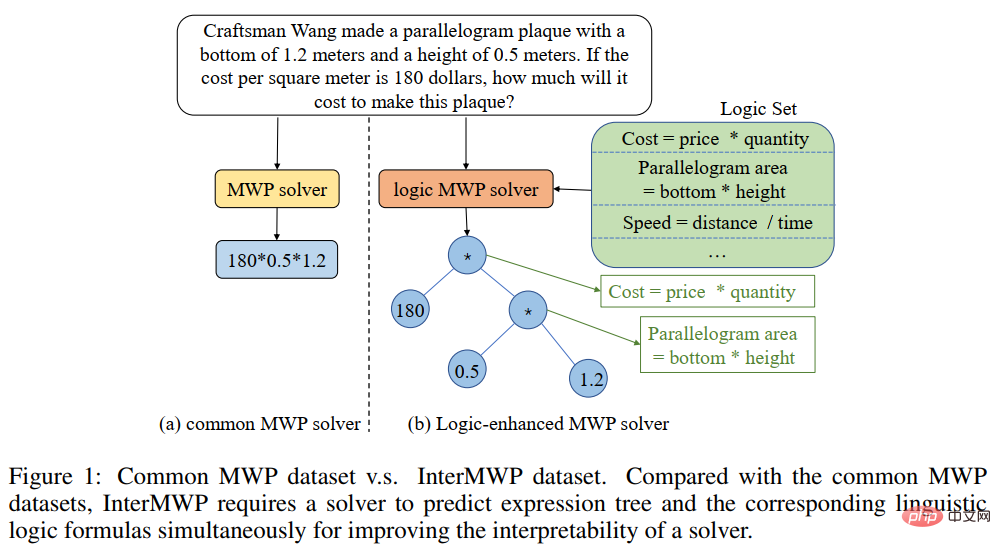
Rajah 8 Contoh set data InterMWP
Untuk menggunakan pengetahuan logik matematik dan memperkasakan penyelesai masalah MWP dengan kebolehtafsiran, pasukan kami terus membina rangka kerja penyelesaian masalah aplikasi matematik baharu LogicSolver, seperti yang ditunjukkan dalam Rajah 9. Rangka kerja ini mengekstrak pengetahuan logik yang berkaitan daripada perpustakaan formula logik sebagai maklumat segera melalui pengambilan semula, menambah baik perwakilan semantik MWP oleh pengekod soalan dan meningkatkan keupayaan penjanaan penjelasan logik MWP.
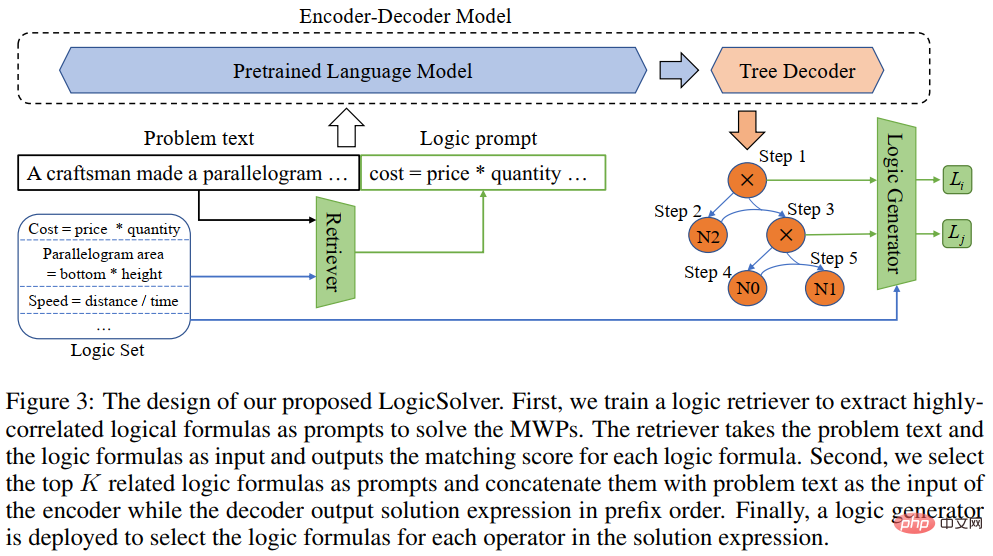
Rajah 9 LogicSolver diagram reka bentuk
LogicSolver terutamanya terdiri daripada tiga komponen utama: komponen perolehan pengetahuan logik, penyelesai MWP yang dipertingkat dengan segera logik dan komponen penjanaan penjelasan. Komponen pencarian pengetahuan logik. Bagi setiap MWP, kami mendapatkan semula formula logik yang sangat relevan daripada 210 formula logik sebagai petunjuk untuk meningkatkan penyelesaian MWP. Kami menyambungkan gesaan formula logik dengan teks soalan sebagai input untuk memacu model MWP untuk menjana ungkapan penyelesaian. Akhir sekali, untuk mendapatkan penjelasan berdasarkan formula logik, kami menggunakan penjana logik untuk meramalkan formula logik yang sepadan dengan setiap nod dalaman (iaitu, operator) pokok ungkapan logik sebagai penjelasan untuk penyelesaian.
Dalam percubaan, kami membina berbilang model garis dasar pada set data InterMWP dan membandingkan LogicSolver kami dengan model garis dasar ini. Keputusan eksperimen ditunjukkan dalam jadual di bawah.
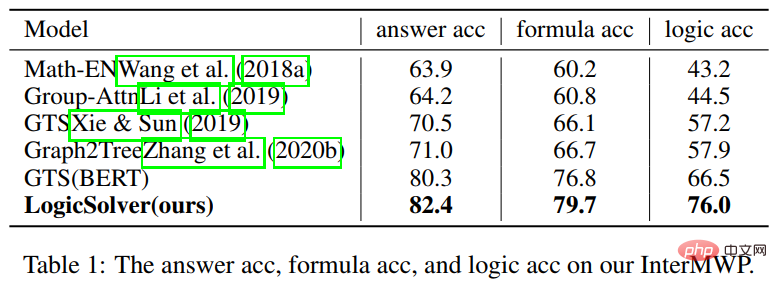
Seperti yang dapat dilihat daripada keputusan percubaan, LogicSolver kami boleh dipertingkatkan dalam ketepatan jawapan, ketepatan formula dan ketepatan formula logik , yang menunjukkan bahawa LogicSolver kami boleh mempunyai kebolehtafsiran logik yang lebih baik (Logic Acc) sambil meningkatkan prestasi penyelesaian (Jawapan Acc dan Formula Acc). Untuk butiran penyelidikan lanjut, sila rujuk kertas asal.
Kertas 6: UniGeo: Menyatukan Geometri Penaakulan Logik melalui Merumus Semula Ungkapan Matematik
Jiaqi Chen, Tong Li, Jinghui Qin, Pan Lu, Liang Lin, Chongyu Chen dan Xiaodan Liang
Persidangan 2022 mengenai Kaedah Empirikal dalam Pemprosesan Bahasa Semulajadi
Penyelesaian automatik masalah geometri ialah penanda aras untuk menilai keupayaan penaakulan pelbagai mod model mendalam. Walau bagaimanapun, dalam kebanyakan kerja sedia ada, penyelesaian automatik masalah pengiraan geometri dan pembuktian automatik masalah geometri dianggap sebagai dua tugas yang berbeza, dan pemprosesan anotasi berbeza digunakan, yang menghalang penaakulan bersatu model mendalam dalam tugasan matematik yang berbeza. Pada dasarnya, soalan pengiraan geometri dan soalan bukti geometri mempunyai ungkapan masalah yang sama dan bertindih dalam pengetahuan matematik yang diperlukan untuk menyelesaikannya. Oleh itu, perwakilan bersatu dan pembelajaran dua tugas menyelesaikan masalah pengiraan geometri secara automatik dan menyelesaikan masalah geometri secara automatik boleh membantu meningkatkan pemahaman semantik dan penaakulan simbolik model mendalam untuk kedua-dua masalah ini.
Untuk tujuan ini, pasukan Makmal Gabungan Perisikan Manusia-Mesin Universiti Sun Yat-sen telah membina UniGeo, set data penanda aras yang mengandungi beribu-ribu soalan geometri. UniGeo termasuk 4,998 masalah pengiraan geometri dan 9,543 masalah bukti geometri. Kami menyediakan anotasi bukti berbilang langkah untuk setiap masalah bukti, dan anotasi ini boleh ditukar dengan mudah kepada program simbolik boleh laku. Soalan pengiraan juga menggunakan anotasi yang serupa, seperti yang ditunjukkan dalam Rajah 10. Selepas anotasi seperti yang ditunjukkan dalam Rajah 10, UniGeo boleh mewakili masalah pengiraan geometri dan masalah pembuktian geometri dalam bahasa simbolik formal.
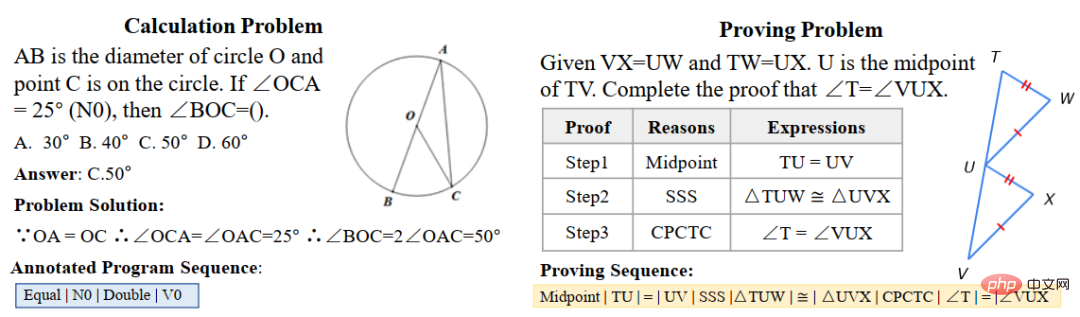
Rajah 10 sampel data UniGeo
Selepas menggunakan bahasa simbolik formal untuk menganotasi soalan pengiraan geometri dan soalan bukti geometri secara seragam, untuk mengesahkan bahawa perwakilan bersatu bagi kedua-dua soalan ini boleh menggalakkan pemahaman semantik model dan keupayaan penaakulan simbolik untuk soalan pengiraan geometri dan soalan bukti geometri, Ini membolehkan penyelesaian masalah pengiraan dan pembuktian masalah pembuktian yang lebih cekap. Pasukan Makmal Integrasi Pintar Objek-Mesin Manusia Universiti Sun Yat-sen membina Geoformer untuk pemprosesan bersepadu penyelesaian masalah geometri dan bukti untuk mengendalikan masalah pengiraan geometri dan masalah bukti geometri pada masa yang sama, seperti yang ditunjukkan dalam Rajah 11.
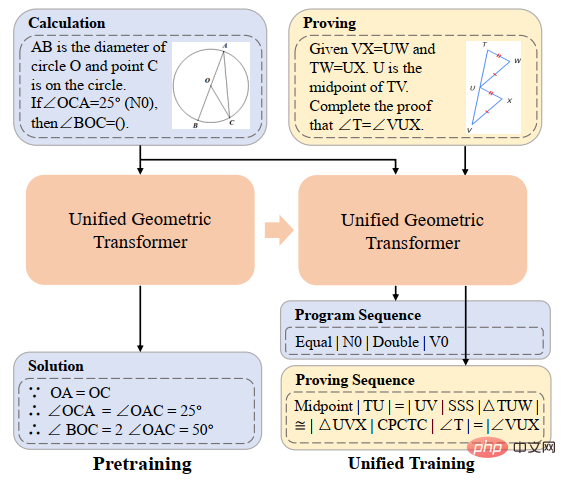
Rajah 11 GeoFormer diagram
Dalam Selain itu , Untuk mempelajari Geoformer yang cekap untuk mencapai penaakulan geometri bersatu, pasukan Makmal Gabungan Perisikan Mesin-Manusia Universiti Sun Yat-sen mencadangkan lagi tugas pra-latihan ungkapan matematik, dan menggabungkan tugas MLM untuk melaksanakan tugas pra-latihan pada Geoformer, seperti yang ditunjukkan dalam Rajah 12.
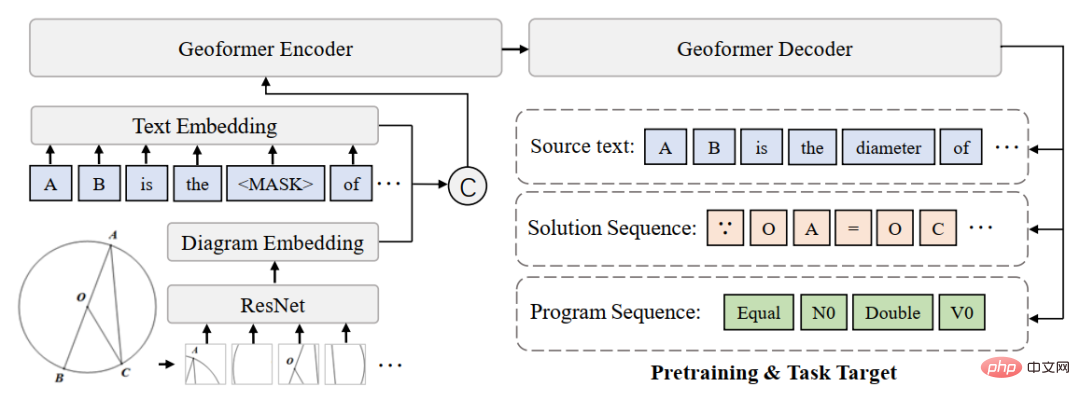
Rajah 12 Rajah skematik ungkapan matematik pra-latihan
Dalam percubaan, kami membina berbilang model garis dasar berdasarkan penanda aras UniGeo dan membandingkan prestasi GeoFormer kami yang dicadangkan. Keputusan eksperimen ditunjukkan dalam jadual di bawah.
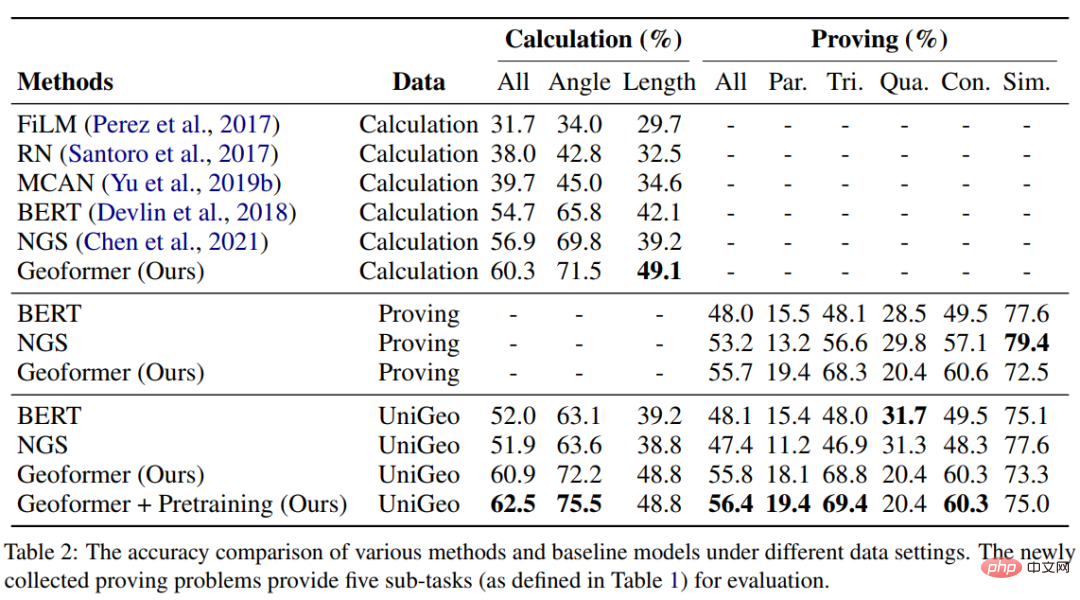
Seperti yang dapat dilihat daripada keputusan percubaan, GeoFormer yang kami cadangkan boleh mencapai hasil yang lebih baik daripada model garis dasar pada kedua-dua pengiraan dan sub-dataset bukti Prestasi keseluruhan yang baik. Begitu juga, GeoFormer adalah lebih unggul daripada model garis dasar NGS dan BERT pada set data penuh yang memerlukan penyelesaian bersatu bagi masalah pengiraan dan pembuktian. Selepas pralatihan ungkapan matematik dan pralatihan MLM, GeoFormer+Pralatihan akan mempunyai peningkatan prestasi selanjutnya berbanding GeoFormer. Keputusan eksperimen ini membuktikan sepenuhnya keberkesanan GeoFormer, dan juga menggambarkan bahawa penaakulan model bersatu untuk masalah pengiraan geometri dan masalah bukti geometri juga membantu untuk tugas masing-masing.
Kerja ini telah disertakan dalam persidangan utama EMNLP2022, sila nantikan butiran penyelidikan lanjut.
Kertas 7: Pra-latihan Penyulingan Kontrastif berasaskan templat untuk Penyelesaian Masalah Perkataan Matematik
Jinghui Qin*, Zhicheng Yang*, Jiaqi Chen, Xiaodan Liang dan Liang Lin
Walaupun model pembelajaran mendalam telah mencapai kemajuan yang baik dalam bidang penyelesaian masalah matematik, model ini mengabaikan The logik penyelesaian yang terkandung dalam huraian masalah, dan logik penyelesaian masalah ini selalunya boleh sepadan dengan templat penyelesaian (penyelesaian). Seperti yang ditunjukkan dalam Rajah 13, dua masalah perkataan yang berbeza setiap satunya boleh sepadan dengan penyelesaian yang sama.
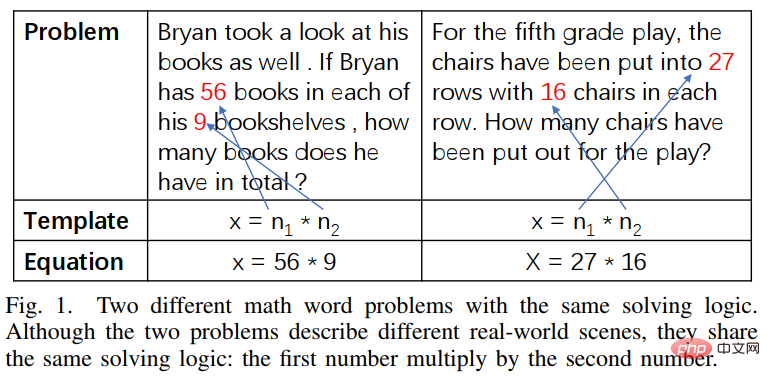
Rajah 13 Contoh masalah perkataan dengan huraian bahasa yang berbeza tetapi penyelesaian yang sama
Selain itu, model bahasa pra-latihan (PLM) mengandungi pengetahuan yang kaya dan keupayaan untuk mempunyai perwakilan semantik berkualiti tinggi, yang akan membantu dalam menyelesaikan masalah MWP.
Untuk menggunakan sepenuhnya pengetahuan yang kaya yang terkandung dalam model bahasa pra-latihan dan menggunakan logik penyelesaian untuk menyelesaikan masalah aplikasi dengan lebih cekap, Sun Yat-sen University Human-Machine -Pasukan Makmal Integrasi Pintar Jirim mencadangkan templat penyelesaian berdasarkan Perbandingan dengan model bahasa pra-latihan Kaedah pra-latihan penyulingan melaksanakan pra-latihan domain pada pengekod masalah dalam penyelesai, seperti yang ditunjukkan dalam Rajah 14. Kaedah ini menggunakan pembelajaran kontrastif pelbagai perspektif untuk mempertimbangkan pengetahuan logik matematik secara berkesan sambil menggunakan penyulingan pengetahuan untuk mengekalkan pengetahuan dan keupayaan perwakilan semantik berkualiti tinggi secara berkesan dalam model bahasa pra-latihan.
Secara khusus, kami mula-mula menggunakan sama ada templat penyelesaian antara kedua-dua soalan adalah konsisten sebagai penunjuk untuk menentukan sama ada kedua-dua soalan itu harus berdekatan antara satu sama lain dalam ruang perwakilan. Kemudian, kami mencadangkan pembelajaran perbandingan pelbagai perspektif, yang melibatkan pembelajaran perbandingan daripada pengekod guru, pengekod pelajar dan pengekod Momentum yang sepadan, supaya dua perwakilan soalan dengan templat penyelesaian yang sama boleh berinteraksi antara satu sama lain dalam ruang perwakilan guru dan perwakilan pelajar Ruang dekat untuk mencapai suntikan logik penyelesaian. Di samping itu, untuk mengekalkan sebanyak mungkin pengetahuan dan keupayaan perwakilan berkualiti tinggi yang terkandung dalam pengekod pelajar yang dimulakan dengan model bahasa pra-latihan, kami menggunakan penyulingan pengetahuan untuk mengekang perwakilan pengekod pelajar dengan menggunakan perwakilan ciri. pengekod guru sebagai penyeliaan Untuk mempunyai keupayaan perwakilan yang sama seperti pengekod guru terlatih, dengan itu mencapai pemeliharaan semantik.
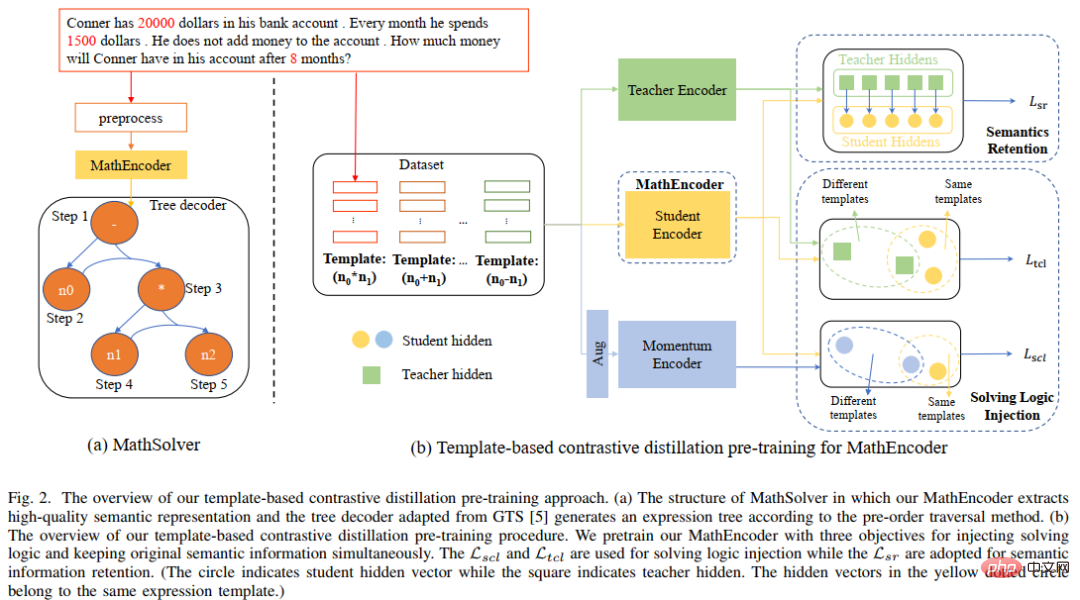
Rajah 14 Kaedah pra-latihan penyulingan perbandingan berdasarkan templat penyelesaian dan model bahasa pra-latihan
Dalam eksperimen, kami menggunakan model bahasa pra-latihan yang berbeza sebagai permulaan dan mengesahkan kesan kaedah kami. Kami memulakan pengekod masalah MathEncoder dengan berat asas BERT dan berat asas Roberta, dan menggunakan penyahkod dalam GTS sebagai penyahkod ungkapan. Kami secara kolektif merujuk kepada penyelesai berdasarkan MathEncoder sebagai MathSolver. Kami membandingkan MathSolver dengan pelbagai kaedah pada Math23K dan CM17K. Keputusan eksperimen ditunjukkan dalam jadual di bawah.
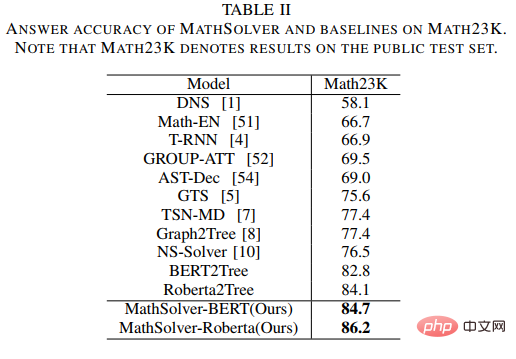
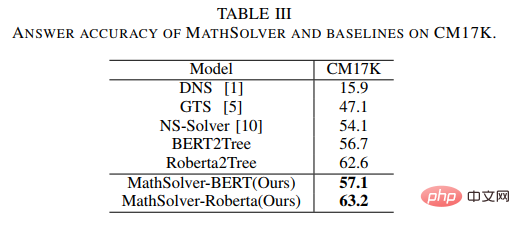
Seperti yang dapat dilihat daripada keputusan eksperimen, kaedah yang kami cadangkan boleh menambah baik penyelesaian bagi kebolehan soalan penyelesai, dan boleh digunakan pada pelbagai model bahasa pra-latihan yang berbeza. Keputusan telah diserahkan kepada Transaksi IEEE pada Rangkaian Neural dan Sistem Pembelajaran, sila nantikan butiran lanjut.
Kertas 8: Kaedah Pengukuhan Data Introspektif untuk Melatih Penyelesai Masalah Perkataan Matematik
Jinghui Qin, Zhongzhan Huang, Ying Zeng, dan Liang Lin
Dalam beberapa tahun kebelakangan ini, semakin ramai penyelidik telah mula mengkaji kaedah berdasarkan pembelajaran mendalam untuk menyelesaikan masalah aplikasi matematik secara automatik, kerana matematik Menyelesaikan masalah aplikasi secara automatik boleh menunjukkan tahap kecerdasan mesin sepenuhnya. Oleh kerana menganotasi set data MWP berkualiti tinggi dan berskala besar adalah sangat mahal, seperti memerlukan pengetahuan profesional dengan tahap pendidikan yang sepadan dan data soalan boleh diakses berskala besar, skala set data MWP berkualiti tinggi sedia ada tidak mencukupi untuk melatih MWP yang cekap. penyelesaian. mesin soalan tidak mencukupi.
Masalah kesesakan data MWP menggalakkan kami berfikir tentang cara menggunakan kaedah penambahan data kos efektif untuk meningkatkan kecekapan penggunaan data dan meningkatkan prestasi penyelesai. Kaedah peningkatan data yang paling langsung ialah kaedah peningkatan data berdasarkan input, seperti penggantian aksara yang biasa digunakan, pemadaman aksara, dll. Walau bagaimanapun, kaedah jenis ini tidak sesuai untuk MWP, kerana MWP mempunyai ciri-ciri ringkas dan ringkas, yang akan mengganggu teks input Atau pengubahsuaian mungkin membuat maksud soalan tidak jelas. Selain itu, hubungan matematik yang terkandung dalam maksud soalan tidak boleh diubah, tetapi kaedah jenis ini berkemungkinan mengubah hubungan matematik yang terkandung dalam maksud soalan, seperti yang ditunjukkan dalam Rajah 15.
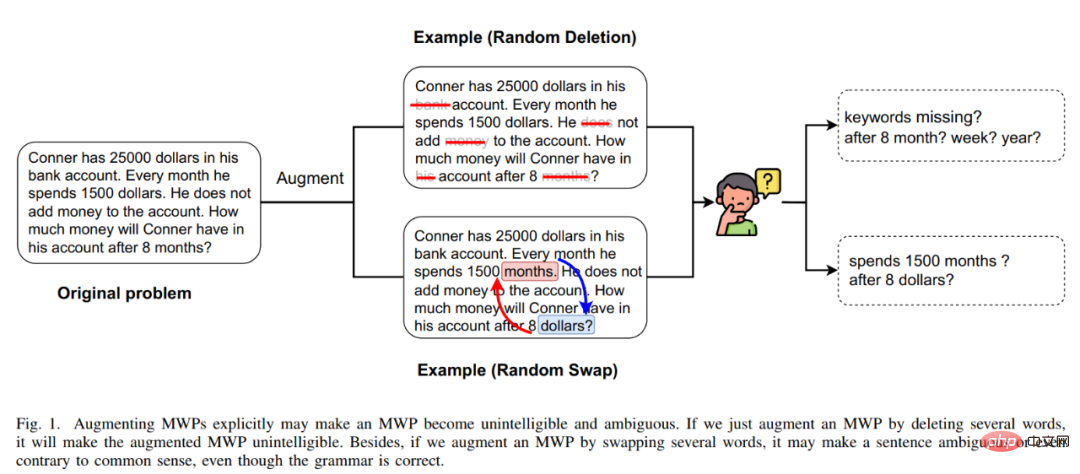
Rajah 15 Contoh kaedah penambahan data berasaskan input tidak sesuai untuk tugas MWP
Selain itu, pasukan Makmal Integrasi Pintar Objek-Mesin Manusia Universiti Sun Yat-sen juga menjalankan pengesahan tertentu bagi kaedah peningkatan data berasaskan input Keputusan eksperimen ditunjukkan dalam Rajah 16. Keputusan eksperimen menunjukkan bahawa kaedah penambahan data eksplisit berasaskan input tidak boleh digunakan untuk tugas MWP dan tidak dapat mengurangkan masalah kesesakan data yang dihadapi oleh tugas MWP dengan berkesan.
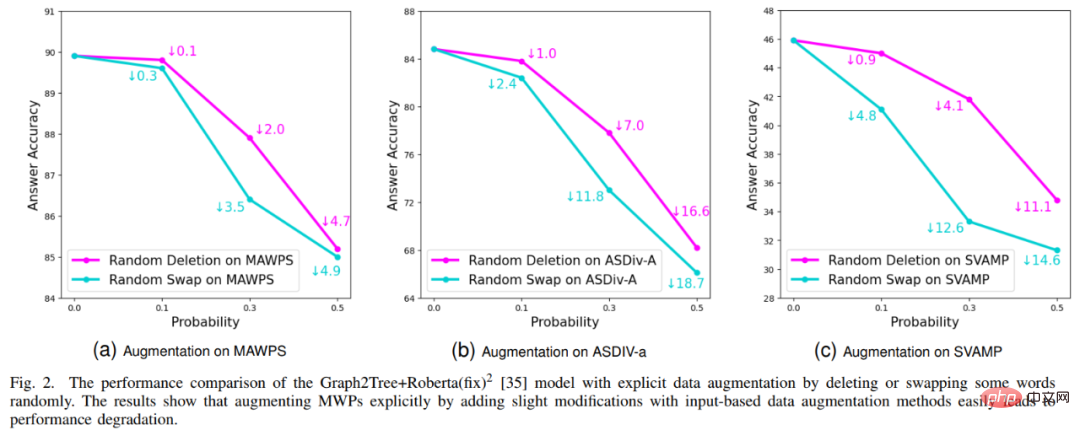
Rajah 16 Kaedah penambahan data berasaskan input tidak dapat meningkatkan kesan penyelesaian masalah MWP
Untuk tujuan ini, kami mencadangkan kaedah peningkatan data yang mudah dan cekap sesuai untuk data MWP - kaedah penambahan data introspektif (IDAM) Semasa proses latihan, perwakilan soalan dalam ruang terpendam dilakukan, sekali gus menyelesaikan masalah yang dihadapi oleh kaedah peningkatan data berasaskan input dalam tugasan penyelesaian MWP. Kaedah IDAM melaksanakan kaedah pembinaan perwakilan yang berbeza (penghimpunan min, pengagregatan hierarki, pembuangan rawak, pertukaran rawak, dll.) dengan mengekodkan perwakilan masalah untuk mendapatkan perwakilan masalah baharu, dan kemudian menggunakan fungsi objektif ketekalan (berdasarkan ungkapan antara JS divergence) untuk mengekang keluaran penyahkodan ungkapan penyelesai berdasarkan perwakilan masalah baharu agar konsisten dengan keluaran penyahkodan ungkapan berdasarkan perwakilan masalah asal. Gambarajah skematik kaedah ditunjukkan dalam Rajah 17.
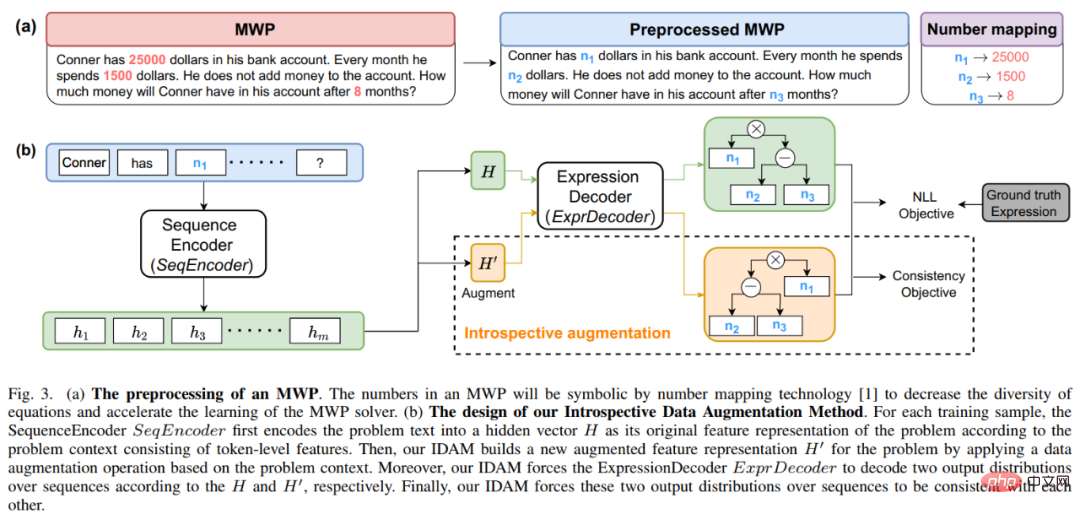
Rajah 17 Diagram skematik kaedah penambahan data introspektif (IDAM)
Dalam percubaan, kami membenamkan IDAM ke dalam berbilang kaedah SOTA dan membandingkannya pada berbilang set data, mengesahkan keberkesanan dan serba boleh kaedah IDAM kami. Keputusan eksperimen ditunjukkan dalam jadual di bawah. Ia boleh dilihat daripada keputusan percubaan bahawa di bawah konfigurasi percubaan yang sama, IDAM kami boleh meningkatkan prestasi model garis dasar penyelesai yang berbeza pada set data MWP yang berbeza. Ini menggambarkan sepenuhnya keberkesanan pendekatan IDAM kami terhadap masalah MWP.
Keputusan ini telah diserahkan kepada Transaksi IEEE/ACM mengenai Pemprosesan Audio, Pertuturan dan Bahasa, sila nantikan butiran lanjut.
Pengenalan Makmal
Makmal Penumpuan Perisikan Manusia-Komputer Universiti Sun Yat-sen (HCP Lab) telah diasaskan pada 2010 oleh Profesor Lin Li Topik penyelidikan mengenai reka letak teknologi kecerdasan buatan termaju telah memenangi hadiah pertama Anugerah Sains dan Teknologi Persatuan Imej dan Grafik China, Anugerah Sains Semula Jadi Wu Wenjun, hadiah pertama sains semula jadi wilayah dan penghormatan lain; telah melatih bakat muda peringkat kebangsaan seperti Liang Xiaodan dan Wang Keze.
Atas ialah kandungan terperinci Pasukan Makmal HCP Universiti Sun Yat-sen: Kejayaan baharu dalam penyelesaian masalah AI, rangkaian saraf membuka pintu kepada penaakulan matematik. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

