Penyelidikan PNAS terkini: 81% kadar penyelesaian masalah, rangkaian saraf Codex membuka pintu kepada dunia matematik lanjutan

Baru-baru ini, satu kajian baharu telah diterbitkan dalam PNAS, yang sekali lagi menyegarkan keupayaan rangkaian saraf. Kali ini rangkaian saraf digunakan untuk menyelesaikan masalah matematik lanjutan, dan ia adalah masalah matematik yang sukar dalam kursus matematik MIT!

Dalam kajian baharu ini, pasukan penyelidik membuktikan bahawa model Codex OpenAI boleh melakukan sintesis program untuk menyelesaikan masalah matematik berskala besar, dan secara automatik menyelesaikan 81% set data melalui pembelajaran sampel kecil masalah kursus matematik, dan Codex mencapai prestasi peringkat manusia dalam tugasan ini.

Pautan asal: https://www.pnas.org/doi/10.1073/pnas.2123433119

Kemunculan penyelidikan ini telah mematahkan konsensus umum bahawa rangkaian saraf tidak dapat menyelesaikan masalah matematik lanjutan. Pasukan penyelidik menegaskan bahawa sebab mengapa Codex boleh mencapai keupayaan sedemikian adalah tepat kerana pasukan itu telah membuat inovasi besar pada masa lalu yang tidak berjaya hanya menggunakan pra-latihan berasaskan teks, dan rangkaian saraf Codex yang muncul kali ini bukan. hanya Pra-latihan dilakukan berdasarkan teks, dan kod itu juga diperhalusi.

Set data masalah yang dikaji telah dipilih daripada enam kursus matematik di MIT dan satu kursus matematik di Columbia University 25 masalah dipilih secara rawak daripada tujuh kursus: Kamiran Pembezaan Univariable MIT, kalkulus multivariable, persamaan pembezaan, pengenalan kepada kebarangkalian dan statistik, algebra linear dan matematik untuk sains komputer dan COMS3251 Computational Linear Algebra dari Columbia University.

Pada masa yang sama, pasukan penyelidik menggunakan MATH, penanda aras masalah matematik lanjutan terkini yang digunakan untuk menilai penaakulan matematik, untuk menguji keupayaan OpenAI Codex yang diambil daripada 6 matematik utama bahagian: Algebra Junior , 15 masalah setiap satu daripada Algebra, Pengiraan dan Kebarangkalian, Algebra Pertengahan, Teori Nombor dan Prakalkulus.

Kapsyen: Set data soalan kursus dan penanda aras MATH yang digunakan dalam kajian

Penyelidikan menunjukkan bahawa Codex menyelesaikan 265 masalah dalam set data masalah dan set data MATH, 213 daripadanya diselesaikan secara automatik.

1 Di manakah inovasi

Selepas keluaran Transformer, model bahasa berdasarkan Transformer telah digunakan dalam pelbagai pemprosesan bahasa semula jadi (NLP ) tugasan, termasuk Ia telah mencapai kejayaan besar dalam tugasan bahasa sifar pukulan dan beberapa pukulan. Tetapi kerana Transformer hanya pra-latihan pada teks, model ini pada asasnya tidak dapat menyelesaikan masalah matematik GPT-3 adalah contoh biasa.

Kemudian, melalui pembelajaran beberapa pukulan dan gesaan Chain-of-thought (CoT), keupayaan penaakulan matematik GPT-3 bagaimanapun, , tanpa kod, walaupun dengan pukulan kecil pembelajaran dan petunjuk CoT, GPT-3 masih tidak berkuasa pada masalah matematik peringkat kolej dan penanda aras MATEMA.

Penyelidikan lepas tentang penyelesaian masalah matematik mungkin telah mencapai keputusan tertentu pada tahap matematik yang agak mudah. Contohnya, teknik yang mengesahkan atau meramal pepohon ungkapan berdasarkan output latihan kolaboratif, seperti MAWPS dan Math23k, boleh menyelesaikan masalah matematik peringkat sekolah rendah dengan ketepatan lebih 81%, tetapi teknik tersebut tidak dapat menyelesaikan masalah matematik sekolah menengah, matematik Olympiad atau peringkat kolej. masalah matematik. Latihan bersama digabungkan dengan rangkaian neural graf (GNN) untuk meramalkan pokok ungkapan aritmetik membolehkan menyelesaikan masalah peringkat universiti dalam pembelajaran mesin dengan ketepatan sehingga 95%. Tetapi kerja ini juga terhad kepada jawapan berangka, dan menghasilkan overfitting dan tidak boleh digeneralisasikan kepada kursus lain.

Dan salah satu daripada inovasi terbesar karya ini ialah bukan sahaja model Transformer seperti Codex dilatih terlebih dahulu pada teks, tetapi juga pada kod diperhalusi supaya dapat menjana program yang menyelesaikan masalah matematik secara besar-besaran.

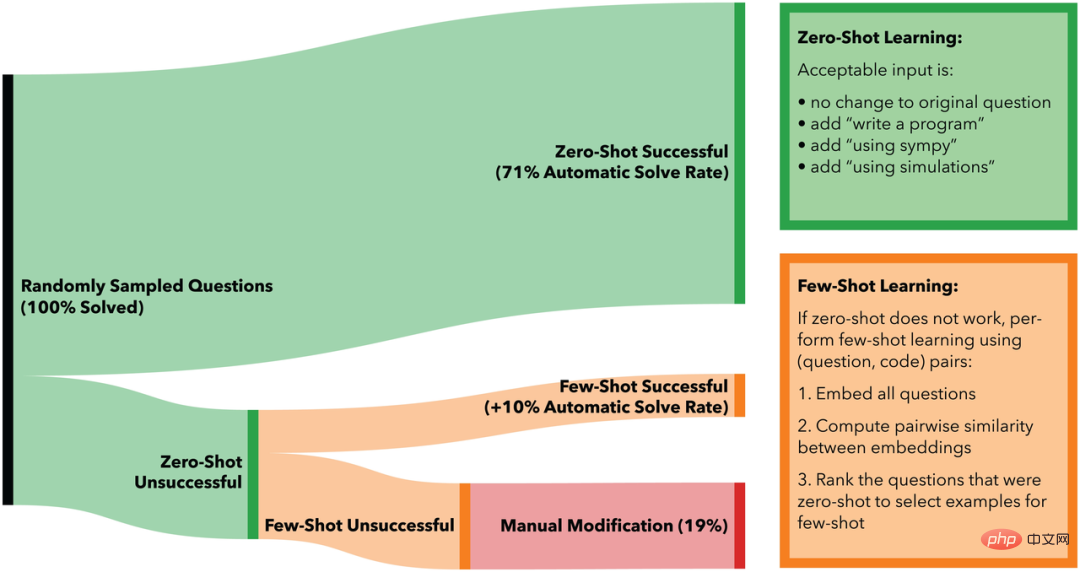
Pasukan penyelidik memilih sampel soalan secara rawak daripada set data yang tidak memerlukan imej input atau bukti untuk ujian. Antaranya, model bahasa yang dilatih hanya pada teks (GPT-3 text-davinci-002) secara automatik menyelesaikan hanya 18% daripada masalah kursus dan 25.5% daripada masalah penanda aras MATH.

Sebaliknya, program yang disintesis menggunakan pembelajaran sifar pukulan dan rangkaian saraf yang dipralatih pada teks dan diperhalusi pada kod (OpenAI Codex code-davinci-002) boleh Diselesaikan secara automatik 71% sudah tentu soalan dan 72.2% daripada soalan tanda aras MATH.

Menggunakan rangkaian neural Codex yang sama serta pembelajaran beberapa pukulan, 81% daripada masalah dalam kursus dan 81.1% daripada masalah dalam ujian penanda aras MATH boleh diselesaikan secara automatik. Walau bagaimanapun, 19% soalan kursus dan 18.9% soalan tanda aras MATH yang model selebihnya tidak dapat menyelesaikan secara automatik akhirnya diselesaikan melalui gesaan manual.

Tambahan kaedah pembelajaran sampel kecil adalah inovasi utama kedua penyelidikan ini. Seperti yang dapat dilihat daripada rajah di atas, apabila pembelajaran sifar pukulan tidak dapat menjawab soalan, (soalan, kod) pasangan (pasangan) digunakan untuk melaksanakan pembelajaran pukulan kecil:

1 ) Menggunakan OpenAI Enjin pemasukan teks-similarity-babbage-001 membenamkan semua soalan

2) Menggunakan persamaan kosinus terbenam untuk mengira soalan yang diselesaikan daripada kursusnya yang paling serupa dengan soalan; soalan yang belum diselesaikan;

3) Gunakan masalah yang paling serupa dan kod yang sepadan sebagai contoh masalah sampel kecil.

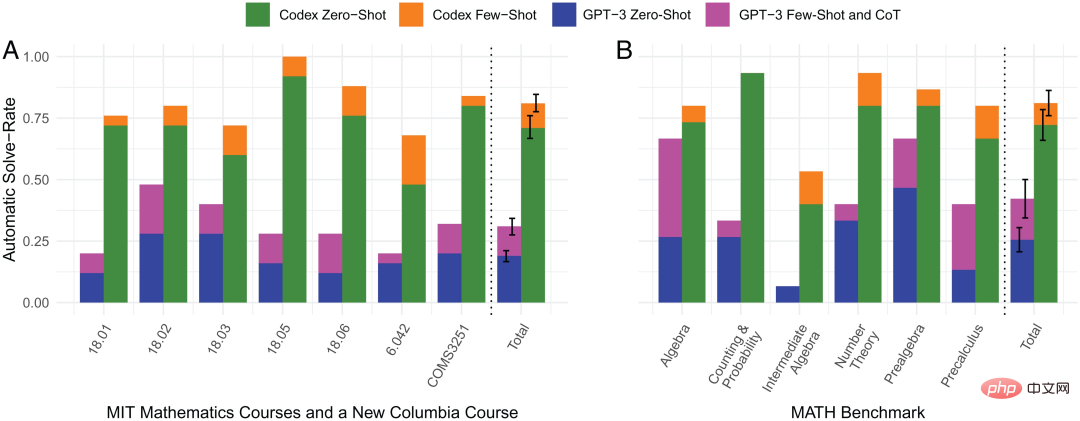
Ilustrasi: Perbandingan kadar penyelesaian masalah automatik bagi 4 kaedah

Rajah di atas menunjukkan perbandingan kadar penyelesaian masalah automatik bagi empat kaedah pembelajaran sampel sifar dan pembelajaran sampel kecil Codex dan pembelajaran sampel sifar dan pembelajaran sampel kecil GPT-3. Ia boleh dilihat daripada rajah bahawa sampel kecil pembelajaran Codex yang diwakili oleh bar oren mempunyai prestasi cemerlang dalam kadar penyelesaian masalah automatik, dan prestasinya pada asasnya dalam setiap bidang matematik adalah lebih kuat daripada tiga kaedah lain.

Inovasi utama ketiga bagi penyelidikan ini ialah ia menyediakan saluran paip untuk menyelesaikan masalah matematik dan menjelaskan mengapa penyelesaiannya begitu. Rajah di bawah menunjukkan MIT 5 The aliran pelaksanaan saluran paip dalam kursus matematik.

Mengambil masalah kalkulus pembolehubah tunggal 18.01 sebagai contoh, memandangkan masalah dan awalan yang dijana secara automatik "Gunakan SymPy", Codex digesa dan mengeluarkan program. Menjalankan atur cara menghasilkan persamaan dengan jawapan yang betul. Program ini kemudian secara automatik meminta Codex sekali lagi, menghasilkan penjelasan kod yang dijana.

2 Selepas menyelesaikan masalah

Selain menyelesaikan masalah matematik dan menerangkan jawapan, Codex juga digunakan untuk menjana soalan baharu bagi setiap kursus.

Untuk menilai tahap soalan yang dihasilkan, pasukan menjalankan tinjauan di kalangan pelajar MIT yang telah mengambil bahagian dalam kursus atau kursus ini pada tahap yang sama, terutamanya untuk membandingkan kualiti mesin -soalan yang dihasilkan dan soalan dan kesukaran yang ditulis secara manual.

Dalam setiap 6 kursus MIT, 5 soalan tulisan tangan dan 5 soalan yang dijana model dicampur dan dibentangkan secara rawak. Bagi setiap 60 soalan, pelajar yang mengambil bahagian diminta menjawab 3 soalan tinjauan:

1) Adakah anda fikir soalan ini ditulis oleh manusia atau dihasilkan oleh mesin?

2) Adakah anda rasa soalan ini sesuai atau tidak sesuai untuk kursus tertentu?

3 ) Pada skala 1 (paling mudah) dan 5 (paling sukar), apakah yang anda akan nilaikan tahap kesukaran masalah ini?

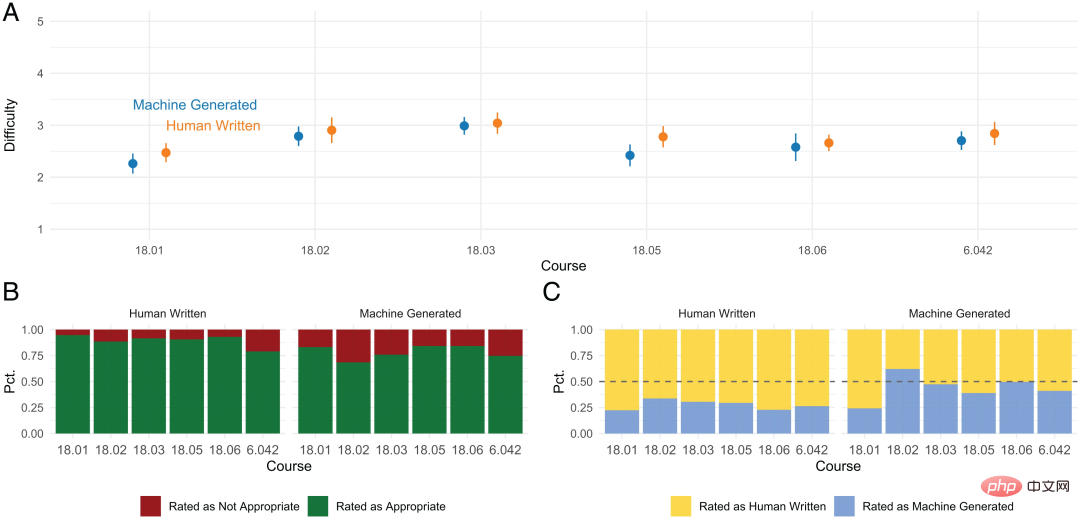
Dalam soal selidik yang dikembalikan, keputusan tinjauan pelajar diringkaskan seperti berikut:

• Kedua-dua soalan yang dihasilkan oleh mesin dan bertulis manusia mempunyai kesukaran yang sama.
• Soalan tulisan manusia lebih sesuai untuk kursus berbanding soalan yang dihasilkan oleh mesin.
• Jawapan tulisan manusia sukar dikenal pasti secara salah, manakala soalan yang dihasilkan mesin dianggap oleh pelajar sama ada dijana mesin atau tulisan manusia.

Soalan yang dijana mesin telah menjadi tidak dapat dibezakan oleh pelajar, menunjukkan bahawa Codex telah mencapai tahap prestasi manusia dalam menjana kandungan baharu.

Walau bagaimanapun, model juga mempunyai masalah yang tidak dapat diselesaikan, seperti ia tidak dapat menjawab jika soalan itu muncul dalam imej atau soalan bukan teks yang lain dengan penyelesaian yang perlu terbukti, Atau masalah sukar diselesaikan secara pengiraan, seperti pemfaktoran nombor perdana yang sangat besar, tidak dapat diselesaikan oleh model ini. Walau bagaimanapun, jenis soalan terakhir ini tidak sepatutnya muncul dalam mana-mana kerja kursus matematik kerana pelajar sebenar pun tidak dapat menjawabnya.

Atas ialah kandungan terperinci Penyelidikan PNAS terkini: 81% kadar penyelesaian masalah, rangkaian saraf Codex membuka pintu kepada dunia matematik lanjutan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!