Apakah yang dikaji oleh Tongji dan Anugerah Kertas Pelajar Terbaik CVPR 2022 Alibaba? Ini adalah tafsiran satu karya

Artikel ini menerangkan kerja kami "EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation" yang memenangi Anugerah Kertas Pelajar Terbaik CVPR 2022. Masalah yang dikaji dalam kertas ini adalah untuk menganggar pose objek dalam ruang 3D berdasarkan imej tunggal. Antara kaedah sedia ada, kaedah anggaran pose berdasarkan pengoptimuman geometri PnP sering mengekstrak titik korelasi 2D-3D melalui rangkaian dalam Walau bagaimanapun, kerana penyelesaian pose yang optimum tidak boleh dibezakan semasa perambatan belakang, adalah sukar untuk menggunakan ralat pose kerana The loss melakukan. latihan rangkaian hujung ke hujung yang stabil, apabila titik korelasi 2D-3D bergantung pada penyeliaan kerugian ejen lain, yang bukan matlamat latihan yang optimum untuk anggaran pose.

Untuk menyelesaikan masalah ini, kami mencadangkan modul EPro-PnP berdasarkan teori, yang mengeluarkan taburan ketumpatan kebarangkalian pose dan bukannya penyelesaian optimum tunggal bagi pose, oleh itu The non -pose optimum yang boleh dibezakan digantikan dengan ketumpatan kebarangkalian yang boleh dibezakan, mencapai latihan hujung ke hujung yang stabil. EPro-PnP sangat serba boleh dan sesuai untuk pelbagai tugas dan data tertentu Ia boleh digunakan untuk menambah baik kaedah anggaran pose berasaskan PnP sedia ada, atau ia juga boleh menggunakan kefleksibelannya untuk melatih rangkaian baharu. Dalam erti kata yang lebih umum, EPro-PnP pada asasnya membawa softmax klasifikasi biasa ke dalam domain berterusan, dan secara teorinya boleh diperluaskan untuk melatih model umum dengan lapisan pengoptimuman bersarang.

Pautan kertas: https://arxiv.org/abs/2203.13254

Pautan kod: https://github.com/tjiiv-cprg/EPro-PnP

1 >

Kami mengkaji masalah klasik dalam penglihatan 3D: mencari objek 3D berdasarkan imej RGB tunggal. Secara khusus, memandangkan imej yang mengandungi unjuran objek 3D, matlamat kami adalah untuk menentukan transformasi badan tegar daripada sistem koordinat objek kepada sistem koordinat kamera. Transformasi badan tegar ini dipanggil pose objek, dilambangkan sebagai y, yang mengandungi dua bahagian: 1) komponen kedudukan, yang boleh diwakili oleh vektor anjakan 3x1 t, 2) komponen orientasi, yang boleh diwakili oleh putaran 3x3 matriks R bermaksud.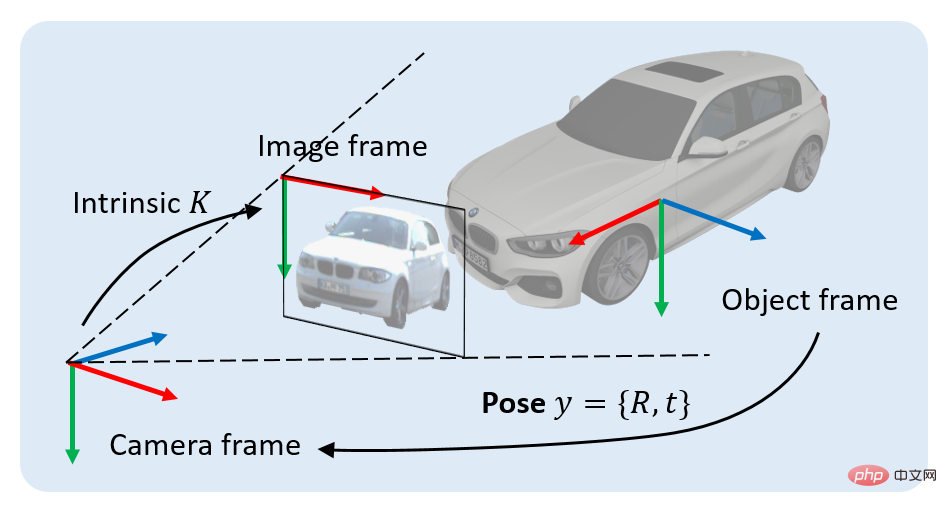

Untuk menangani masalah ini, kaedah sedia ada boleh dibahagikan kepada dua kategori: tersurat dan tersirat. Kaedah eksplisit juga boleh dipanggil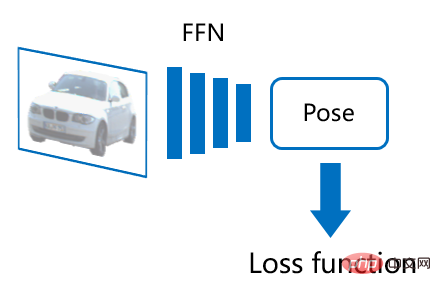

ramalan pose langsung

, iaitu menggunakan rangkaian neural suapan (FFN) untuk mengeluarkan secara terus setiap komponen pose objek, biasanya: 1) meramalkan Kedalaman pose objek, 2) cari kedudukan unjuran 2D titik pusat objek pada imej, 3) ramalkan orientasi objek (kaedah pemprosesan tertentu orientasi mungkin lebih rumit). Menggunakan data imej yang ditandakan dengan pose sebenar objek, fungsi kehilangan boleh direka bentuk untuk menyelia terus hasil ramalan pose, dengan mudah mencapai latihan hujung ke hujung rangkaian. Walau bagaimanapun, rangkaian sedemikian tidak mempunyai kebolehtafsiran dan terdedah kepada pemasangan berlebihan pada set data yang lebih kecil. Dalam tugas pengesanan objek 3D, kaedah eksplisit mendominasi, terutamanya untuk set data yang lebih besar (seperti nuScenes).

Kaedah tersirat ialah kaedah anggaran pose berdasarkan pengoptimuman geometri Wakil yang paling tipikal ialah kaedah anggaran pose berasaskan PnP. Dalam kaedah jenis ini, anda perlu mencari titik N 2D dalam sistem koordinat imej (koordinat 2D titik ke-i ditandakan sebagai ), dan pada masa yang sama cari titik berkaitan dalam sistem koordinat objek N titik 3D (koordinat 3D titik ke-i ditandakan sebagai ), dan kadangkala perlu untuk mendapatkan berat perkaitan setiap pasangan mata. (berat perkaitan pasangan mata ke-i ditandakan sebagai ). Mengikut kekangan unjuran perspektif, N pasangan mata berkaitan berwajaran 2D-3D ini secara tersirat menentukan pose optimum objek. Secara khusus, kita boleh mencari pose objek yang meminimumkan ralat unjuran semula :

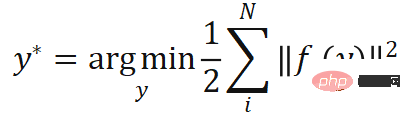
di mana 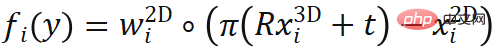, mewakili ralat unjuran semula berwajaran, iaitu fungsi pose. mewakili fungsi tayangan kamera yang mengandungi parameter dalaman dan 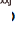mewakili produk elemen. Kaedah PnP biasanya digunakan dalam tugasan anggaran pose 6-DOF di mana geometri objek diketahui.

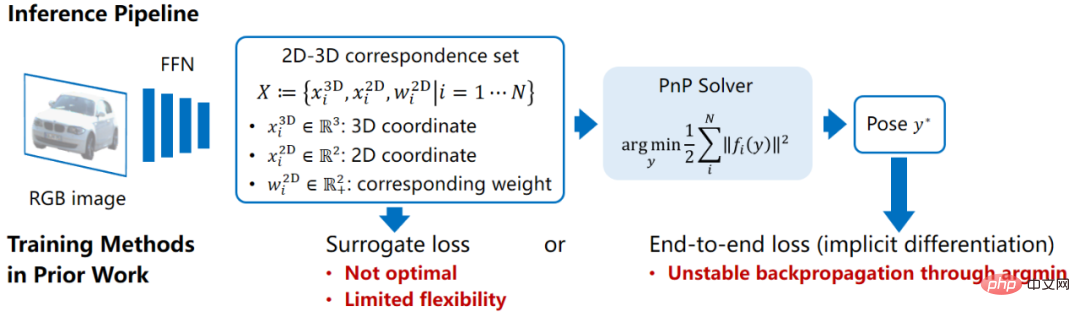
Kaedah berasaskan PnP juga memerlukan rangkaian suapan hadapan untuk meramal set titik berkaitan 2D-3D 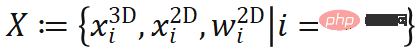. Berbanding dengan ramalan pose langsung, model pembelajaran mendalam yang digabungkan dengan algoritma penglihatan geometri tradisional ini mempunyai kebolehtafsiran yang sangat baik dan prestasi generalisasinya agak stabil Walau bagaimanapun, terdapat kelemahan dalam kaedah latihan model dalam kerja sebelumnya. Banyak kaedah membina fungsi kehilangan proksi untuk menyelia hasil perantaraan X, yang bukan matlamat optimum untuk pose. Contohnya, jika bentuk objek diketahui, titik utama 3D objek boleh dipilih terlebih dahulu, dan kemudian rangkaian dilatih untuk mencari kedudukan titik unjuran 2D yang sepadan. Ini juga bermakna bahawa kerugian pengganti hanya boleh mempelajari subset pembolehubah dalam X dan oleh itu tidak cukup fleksibel. Bagaimana jika kita tidak mengetahui bentuk objek dalam set latihan dan perlu mempelajari segala-galanya dalam X dari awal?

Kaedah tersurat dan tersirat mempunyai kelebihan yang saling melengkapi Jika rangkaian boleh dilatih hujung ke hujung untuk mempelajari set titik X yang berkaitan dengan mengawasi output hasil pose oleh PnP, kedua-duanya. boleh digabungkan Menggabungkan kelebihan. Untuk mencapai matlamat ini, beberapa kajian baru-baru ini telah melaksanakan perambatan balik lapisan PnP menggunakan derivasi fungsi tersirat. Walau bagaimanapun, fungsi argmin dalam PnP adalah tidak berterusan dan tidak boleh dibezakan pada titik tertentu, menjadikan perambatan belakang tidak stabil dan latihan langsung sukar untuk berkumpul.

2. Pengenalan kepada kaedah EPro-PnP

1. -to-end Untuk latihan, kami mencadangkan

end-to-end probabilistik PnP (end-to-end probabilistic PnP), iaitu EPro-PnP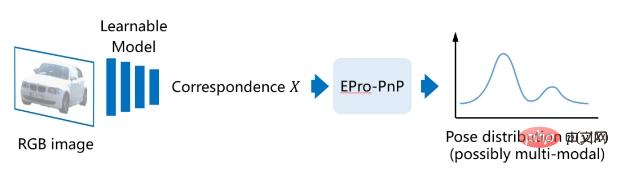. Idea asasnya ialah menganggap pose tersirat sebagai taburan kebarangkalian, maka ketumpatan kebarangkaliannya

boleh dibezakan untuk X. Pertama, fungsi kemungkinan pose ditakrifkan berdasarkan ralat unjuran semula: Jika prior yang tidak bermaklumat digunakan, maka posterior of the pose Ketumpatan kebarangkalian ialah hasil normal bagi fungsi kemungkinan:

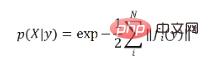
Boleh diperhatikan bahawa formula di atas adalah konsisten dengan formula softmax klasifikasi yang biasa digunakan

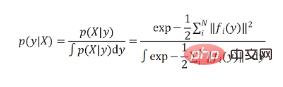mata adalah hampir, sebenarnya, intipati EPro-PnP adalah untuk memindahkan softmax daripada ambang diskret ke ambang berterusan, dan menggantikan penjumlahan

dengan integral

. 2. KL divergence loss Dalam proses melatih model, jika pose sebenar objek diketahui , ia boleh ditakrifkan Taburan pose sasaran

. Pada masa ini, perbezaan KL

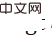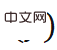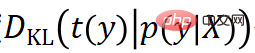
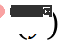
boleh dikira sebagai fungsi kehilangan yang digunakan untuk melatih rangkaian (kerana adalah tetap, ia juga boleh difahami sebagai salib -fungsi kehilangan entropi). Dalam kes di mana sasaran menghampiri fungsi Dirac, fungsi kehilangan berdasarkan perbezaan KL boleh dipermudahkan kepada bentuk berikut: Jika anda mengambil derivatif:

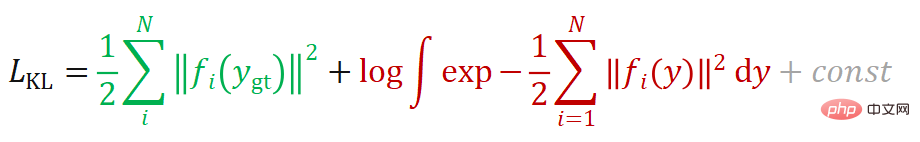
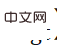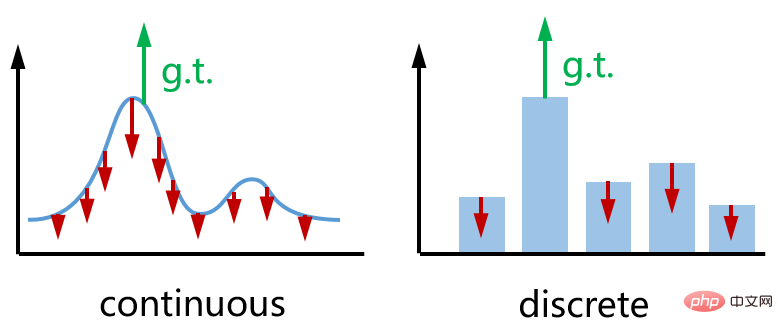
Dapat dilihat bahawa fungsi kehilangan terdiri daripada dua item Istilah pertama (ditandakan sebagai ) cuba untuk mengurangkan unjuran semula nilai sebenar pose Ralat, sebutan kedua (ditandakan sebagai ) cuba meningkatkan ralat unjuran semula di mana-mana dalam pose yang diramalkan . Kedua-dua arah adalah bertentangan, dan kesannya ditunjukkan dalam rajah di bawah (kiri). Sebagai analogi, bahagian kanan ialah kerugian rentas entropi kategori yang biasa kami gunakan semasa melatih rangkaian klasifikasi.

3. Monte Carlo pose loss

Perlu diingatkan bahawa penggal kedua di KL rugi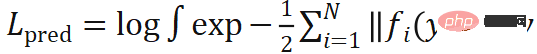 mengandungi kamiran ini tidak mempunyai penyelesaian analitik, jadi ia mesti dianggarkan dengan kaedah berangka. Memandangkan fleksibiliti, ketepatan dan kecekapan pengiraan, kami menggunakan kaedah Monte Carlo untuk mensimulasikan pengedaran pose melalui pensampelan.

Secara khusus, kami menggunakan algoritma pensampelan kepentingan - Persampelan Kepentingan Pelbagai Adaptif (AMIS) untuk mengira K Kami memanggil proses ini Monte Carlo PnP untuk sampel pose 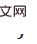dengan pemberat :

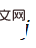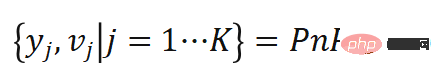
Menurut ini, penggal kedua boleh dianggarkan sebagai fungsi tentang berat 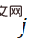, dan 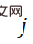boleh Backpropagation:

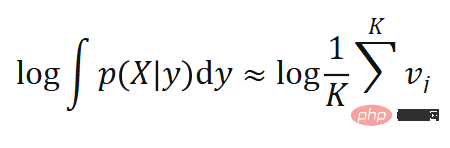
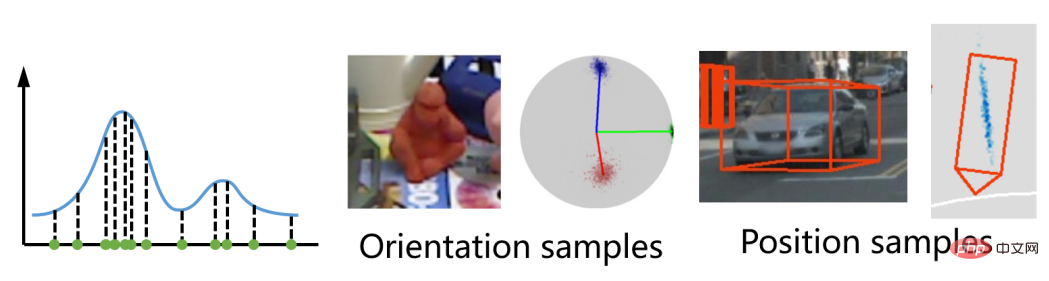
Kesan visualisasi persampelan pose adalah seperti yang ditunjukkan di bawah:

4. Regularisasi terbitan untuk penyelesai PnP

Walaupun kehilangan PnP Monte Carlo boleh digunakan untuk melatih rangkaian untuk mendapatkan pengedaran pose berkualiti tinggi, dalam peringkat inferens, PnP masih diperlukan Optimumkan penyelesai untuk mendapatkan penyelesaian pose yang optimum . Algoritma Gauss-Newton yang biasa digunakan dan derivatifnya menyelesaikan melalui pengoptimuman lelaran, dan kenaikan lelarannya ditentukan oleh derivatif pertama dan kedua bagi fungsi kos . Untuk menjadikan penyelesaian PnP 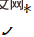lebih hampir kepada nilai sebenar 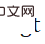, derivatif fungsi kos boleh diselaraskan. Fungsi kehilangan regularisasi direka bentuk seperti berikut:

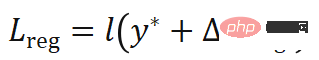
di mana, 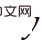ialah kenaikan lelaran Gauss-Newton, dan fungsi kos Terbitan tertib pertama dan kedua adalah berkaitan dan boleh disebarkan balik mewakili metrik jarak, menggunakan L1 licin untuk kedudukan dan persamaan kosinus untuk orientasi. Apabila tidak konsisten, fungsi kehilangan ini menggesa kenaikan lelaran untuk menunjuk kepada nilai sebenar sebenar.

3. Rangkaian anggaran pose berdasarkan EPro-PnP

Kami menggunakan subtugas yang berbeza untuk anggaran pose 6 darjah dan pengesanan sasaran 3D. Antaranya, untuk anggaran pose 6 darjah kebebasan, ia diubah suai sedikit berdasarkan rangkaian CDPN ICCV 2019 dan dilatih dengan EPro-PnP untuk menjalankan kajian ablasi bagi pengesanan sasaran 3D, rangkaian baharu direka berdasarkan FCOS3D; daripada ICCVW 2021. Kepala pengesan surat-menyurat boleh ubah bentuk untuk membuktikan bahawa EPro-PnP boleh melatih rangkaian untuk mempelajari secara langsung semua titik 2D-3D dan pemberat perkaitan tanpa pengetahuan bentuk objek, sekali gus menunjukkan fleksibiliti EPro-PnP dalam aplikasi.

1. Rangkaian korelasi padat untuk anggaran pose 6-DOF

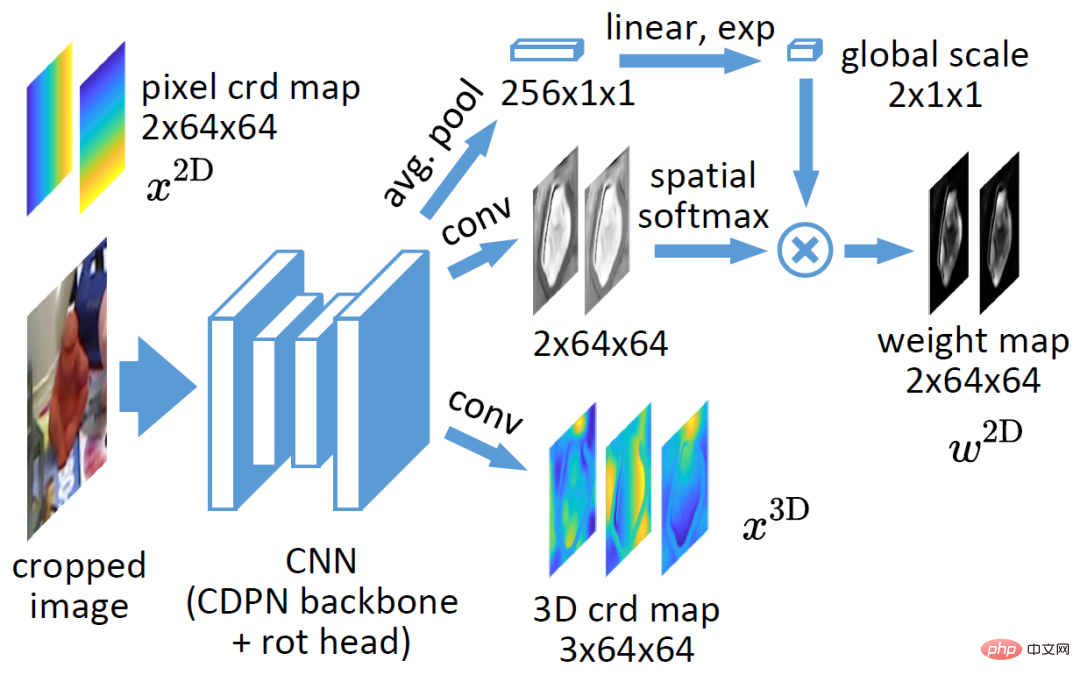
Struktur rangkaian adalah seperti yang ditunjukkan dalam rajah di atas, kecuali lapisan keluaran diubah suai berdasarkan CDPN asal. CDPN asal menggunakan kotak 2D objek yang dikesan untuk memotong imej serantau dan memasukkannya ke dalam tulang belakang ResNet34. CDPN asal memisahkan kedudukan dan orientasi kepada dua cawangan Cawangan kedudukan menggunakan kaedah ramalan langsung yang jelas, manakala cawangan orientasi menggunakan kaedah perkaitan padat dan PnP yang tersirat. Untuk mengkaji EPro-PnP, rangkaian yang diubah suai hanya mengekalkan cawangan korelasi yang padat, yang outputnya ialah peta koordinat 3D 3 saluran dan berat korelasi 2 saluran, di mana berat korelasi telah mengalami softmax spatial dan penskalaan berat global. Tujuan menambah softmax spatial adalah untuk menormalkan pemberat supaya ia mempunyai ciri-ciri yang serupa dengan peta perhatian dan boleh memfokuskan pada kawasan yang agak penting Eksperimen telah membuktikan bahawa normalisasi berat juga merupakan kunci kepada penumpuan yang stabil . Penskalaan berat global mencerminkan kepekatan pengedaran pose . Rangkaian boleh dilatih hanya menggunakan kehilangan pose Monte Carlo bagi EPro-PnP, di samping menambah penyusunan derivatif dan kehilangan regresi koordinat 3D tambahan apabila bentuk objek diketahui.

2. Rangkaian korelasi ubah bentuk untuk pengesanan sasaran 3D

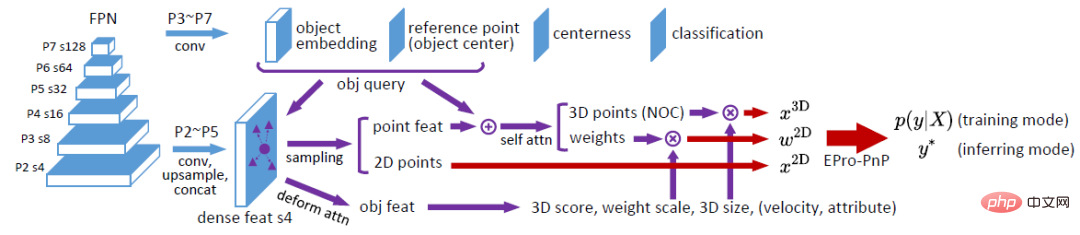
Struktur rangkaian ditunjukkan dalam rajah di atas. Secara umumnya, ia adalah berdasarkan pengesan FCOS3D dan merujuk kepada struktur rangkaian yang direka oleh DETR boleh ubah bentuk. Berdasarkan FCOS3D, lapisan kepusatan dan pengelasannya dikekalkan, dan lapisan ramalan pose asalnya digantikan dengan pembenaman objek dan lapisan titik rujukan untuk menjana pertanyaan objek. Merujuk kepada DETR boleh ubah bentuk, kita mendapat kedudukan pensampelan 2D dengan meramalkan offset relatif kepada titik rujukan (iaitu, kita mendapat ). Ciri sampel diagregatkan ke dalam ciri objek melalui operasi perhatian, yang digunakan untuk meramalkan hasil peringkat objek (skor 3D, skala berat, saiz kotak 3D, dsb.). Di samping itu, selepas pensampelan, ciri setiap titik ditambah dengan pembenaman objek dan diproses oleh perhatian sendiri untuk mengeluarkan koordinat 3D yang sepadan dan pemberat yang berkaitan . yang diramalkan semuanya boleh diperolehi oleh latihan Monte Carlo pose loss EPro-PnP, yang boleh menumpu dan mencapai ketepatan tinggi tanpa regularisasi tambahan. Atas dasar ini, kerugian penyusunan derivatif dan kerugian tambahan boleh ditambah untuk meningkatkan lagi ketepatan.

4. Keputusan eksperimen

1. set data LineMOD Eksperimen dan perbandingan ketat dengan garis dasar CDPN, keputusan utama adalah seperti di atas. Ia boleh dilihat bahawa dengan menambah kerugian EPro-PnP untuk latihan hujung ke hujung, ketepatan meningkat dengan ketara (+12.70). Teruskan meningkatkan kehilangan penyusunan derivatif, dan ketepatan dipertingkatkan lagi. Atas dasar ini, menggunakan keputusan latihan CDPN asal untuk memulakan dan meningkatkan zaman (mengekalkan jumlah bilangan zaman yang konsisten dengan latihan tiga peringkat lengkap CDPN asal) boleh meningkatkan lagi ketepatan sebahagian daripada kelebihan pra-. latihan CDPN datang daripada latihan tambahan penyeliaan topeng CDPN.

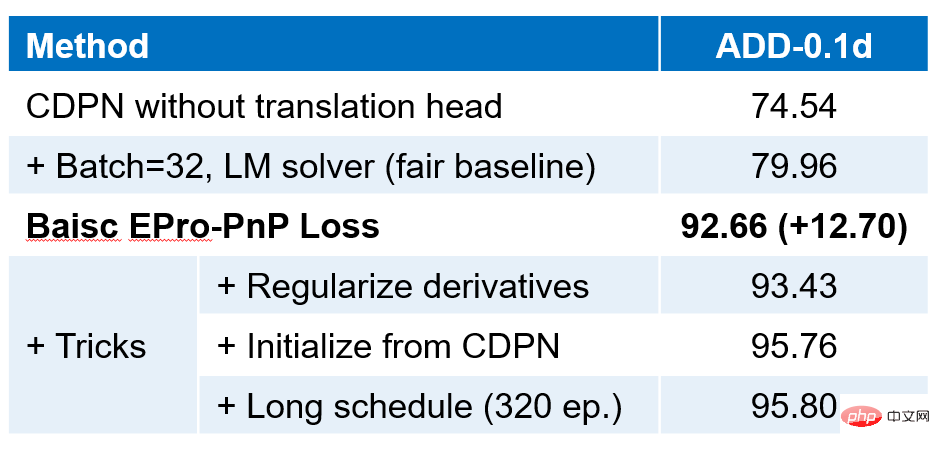
Graf di atas adalah perbandingan EPro-PnP dengan pelbagai kaedah utama. EPro-PnP, yang dipertingkatkan daripada CDPN ke belakang, adalah hampir dengan SOTA dalam ketepatan, dan seni bina EPro-PnP adalah ringkas Ia sepenuhnya berdasarkan PnP untuk anggaran pose dan tidak memerlukan anggaran kedalaman eksplisit atau penghalusan pose. Oleh itu, dalam Terdapat juga kelebihan dalam kecekapan.

2. Tugas pengesanan sasaran 3D

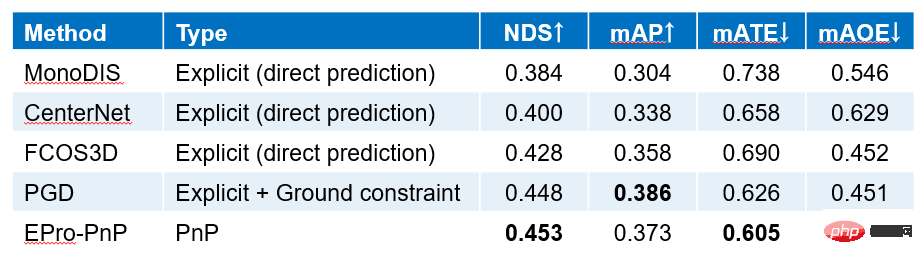
Menggunakan eksperimen set data nuScenes, hasil perbandingan dengan kaedah lain ditunjukkan dalam rajah di atas. EPro-PnP bukan sahaja mempunyai peningkatan ketara berbanding FCOS3D, tetapi juga mengatasi PGD, satu lagi versi SOTA dan FCOS3D yang dipertingkatkan pada masa itu. Lebih penting lagi, EPro-PnP kini merupakan satu-satunya yang menggunakan kaedah pengoptimuman geometri untuk menganggarkan pose pada set data nuScenes. Disebabkan oleh skala besar set data nuScenes, rangkaian anggaran pose langsung terlatih hujung ke hujung sudah mempunyai prestasi yang baik dan keputusan kami menggambarkan bahawa latihan hujung ke hujung model berdasarkan pengoptimuman geometri boleh mencapai prestasi yang lebih baik pada set data yang besar.

3. Analisis visual

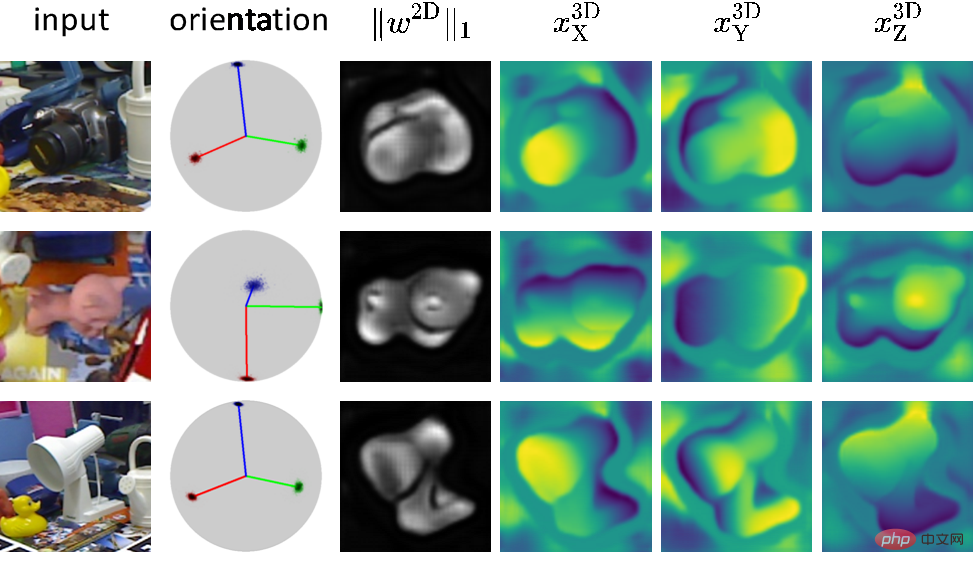
Rajah di atas menunjukkan hasil ramalan rangkaian persatuan padat yang dilatih dengan EPro-PnP. Antaranya, peta berat perkaitan menyerlahkan kawasan penting dalam imej, serupa dengan mekanisme perhatian. Daripada analisis fungsi kehilangan, dapat dilihat bahawa kawasan sorotan sepadan dengan kawasan dengan ketidakpastian unjuran semula yang rendah dan yang lebih sensitif terhadap perubahan pose.

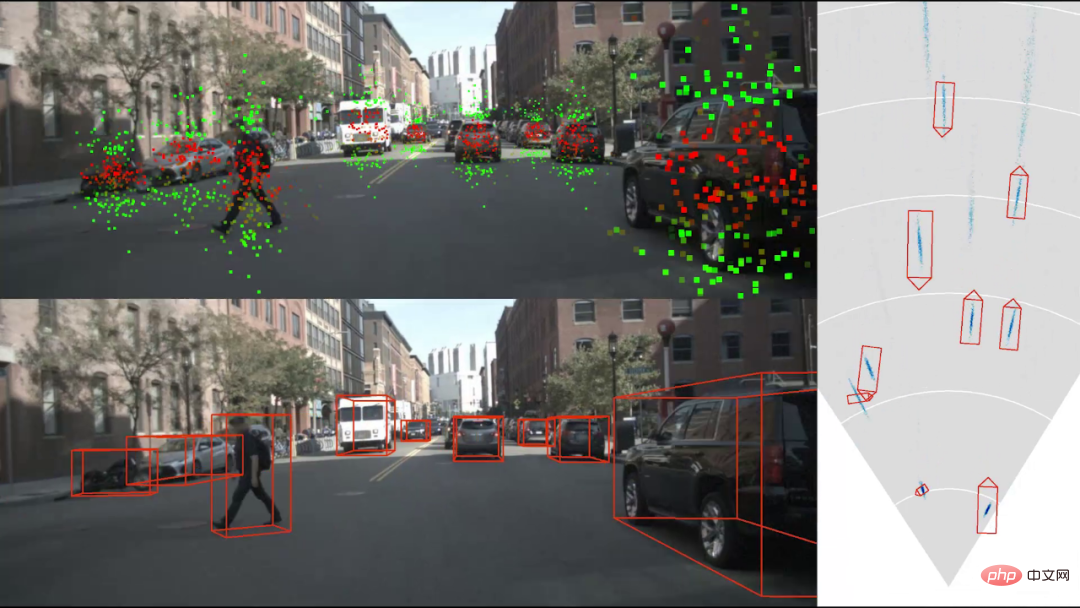
Hasil pengesanan sasaran 3D ditunjukkan dalam rajah di atas. Pandangan kiri atas menunjukkan kedudukan titik 2D yang disampel oleh rangkaian korelasi ubah bentuk Merah menunjukkan bahawa komponen X mendatar adalah agak tinggi, dan hijau menunjukkan bahawa komponen Y menegak adalah agak tinggi . Titik hijau biasanya terletak di hujung atas dan bawah objek Fungsi utamanya adalah untuk mengira jarak objek melalui ketinggian objek. Ciri ini tidak ditentukan secara buatan dan sepenuhnya hasil latihan percuma. Gambar di sebelah kanan menunjukkan hasil pengesanan dalam paparan atas, di mana imej awan biru mewakili ketumpatan pengedaran titik tengah objek, mencerminkan ketidakpastian kedudukan objek. Secara amnya, ketidakpastian kedudukan objek jauh adalah lebih besar daripada objek berdekatan.

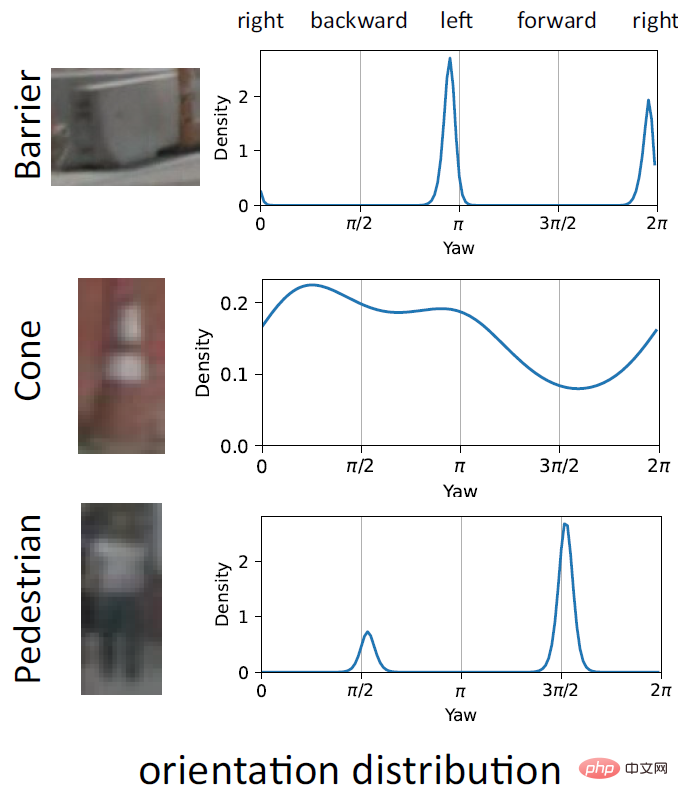Satu lagi kelebihan penting EPro-PnP ialah keupayaan untuk mewakili kekaburan orientasi dengan meramalkan pengagihan multimodal yang kompleks. Seperti yang ditunjukkan dalam rajah di atas, Barrier selalunya mempunyai dua puncak dengan perbezaan 180° kerana simetri putaran objek itu sendiri tidak mempunyai orientasi khusus, jadi hasil ramalan diedarkan dalam semua arah; simetri, tetapi disebabkan oleh imej Ia tidak jelas, sukar untuk memberitahu bahagian depan dan belakang, dan kadang-kadang terdapat dua puncak. Ciri kebarangkalian ini menjadikan EPro-PnP tidak memerlukan sebarang pemprosesan khas pada fungsi kehilangan untuk objek simetri.

5 Ringkasan

EPro-PnP mengubah pose optimum asal yang tidak boleh dibezakan kepada ketumpatan kebarangkalian pose yang boleh dibezakan, menjadikan kedudukan berdasarkan pengoptimuman geometri PnP Rangkaian anggaran pose membolehkan latihan hujung ke hujung yang stabil dan fleksibel. EPro-PnP boleh digunakan untuk masalah anggaran pose 3D am Walaupun geometri objek 3D tidak diketahui, titik berkaitan 2D-3D objek boleh dipelajari melalui latihan hujung ke hujung. Oleh itu, EPro-PnP meluaskan kemungkinan reka bentuk rangkaian, seperti rangkaian korelasi ubah bentuk kami yang dicadangkan, yang sebelum ini mustahil untuk dilatih.

Selain itu, EPro-PnP juga boleh digunakan secara langsung untuk menambah baik kaedah anggaran pose berasaskan PnP sedia ada, melepaskan potensi rangkaian sedia ada melalui latihan hujung ke hujung dan meningkatkan ketepatan anggaran pose. Dalam erti kata yang lebih umum, EPro-PnP pada asasnya membawa klasifikasi softmax ke dalam domain berterusan Ia bukan sahaja boleh digunakan untuk masalah penglihatan 3D lain berdasarkan pengoptimuman geometri, tetapi juga boleh diperluaskan secara teori untuk melatih model pengoptimuman bersarang umum .

Atas ialah kandungan terperinci Apakah yang dikaji oleh Tongji dan Anugerah Kertas Pelajar Terbaik CVPR 2022 Alibaba? Ini adalah tafsiran satu karya. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!