Rumah >Peranti teknologi >AI >Adakah persamaan itu hutan pokok binari? Temui persamaan tadbir urus dan mekanisme fizikal yang tidak diketahui secara langsung daripada data
Adakah persamaan itu hutan pokok binari? Temui persamaan tadbir urus dan mekanisme fizikal yang tidak diketahui secara langsung daripada data
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-08 18:11:041153semak imbas
Penyelidik berharap dapat menggunakan kaedah pembelajaran mesin untuk melombong secara automatik undang-undang intrinsik yang paling berharga dan penting terus daripada data bukan linear berdimensi tinggi (iaitu, untuk melombong persamaan pentadbir berasaskan PDE di sebalik masalah) untuk mencapai penemuan pengetahuan automatik.
Baru-baru ini, pasukan penyelidik dari Institut Teknologi Timur, Universiti Washington, Ruilai Wisdom dan Universiti Peking telah mencadangkan algoritma genetik SGA-PDE berdasarkan matematik simbolik, membina set calon terbuka yang boleh mengekstrak data daripada data . Secara langsung melombong bentuk persamaan yang mengawal.
Eksperimen menunjukkan bahawa SGA-PDE bukan sahaja boleh melombong persamaan Burgers (dengan istilah interaksi), persamaan Korteweg–de Vries (KdV, dengan sebutan terbitan peringkat lebih tinggi), dan persamaan Chafee-Infante (dengan istilah eksponen) daripada istilah data dan istilah terbitan), dan juga berjaya melombong persamaan yang mengawal dengan fungsi komposit dan persamaan dengan struktur pecahan dalam masalah aliran graviti likat, dua yang terakhir sukar ditemui dengan kaedah sebelumnya. SGA-PDE tidak bergantung pada pengetahuan terdahulu tentang borang persamaan dan mengisi jurang dalam masalah perlombongan persamaan kawalan struktur yang kompleks. Model ini tidak memerlukan set persamaan calon untuk diberikan terlebih dahulu, yang bermanfaat kepada aplikasi praktikal algoritma penemuan pengetahuan automatik dalam masalah saintifik yang tidak diketahui.
Kajian itu bertajuk "Algoritma genetik simbolik untuk menemui persamaan pembezaan separa bentuk terbuka (SGA-PDE)" dan diterbitkan dalam Penyelidikan Kajian Fizikal pada 1 Jun.

Idea penemuan pengetahuan umum semasa ialah menggunakan regresi jarang, iaitu, pra-diberikan set calon tertutup, kemudian pilih istilah persamaan daripadanya, dan gabungkan persamaan yang mengawal , seperti SINDy dan PDE-FIND. Walau bagaimanapun, kaedah jenis ini memerlukan pengguna untuk menentukan bentuk kasar persamaan terlebih dahulu, dan kemudian memberikan semua operator pembezaan yang sepadan sebagai istilah fungsi dalam set calon terlebih dahulu Istilah fungsi yang tidak wujud dalam set calon tidak dapat ditemui daripada data . Beberapa kajian terkini cuba menggunakan algoritma genetik untuk mengembangkan set calon, tetapi terdapat had utama dalam penggabungan semula dan mutasi gen, dan masih tidak dapat menjana istilah berfungsi dengan struktur kompleks (seperti struktur pecahan dan fungsi komposit )
Kunci untuk melombong persamaan tadbir bentuk terbuka terus daripada data adalah untuk menjana dan mewakili bentuk arbitrari persamaan mentadbir dengan cara yang mudah untuk dikira, dan untuk menilai ketepatan bentuk persamaan dengan mengukur sejauh mana persamaan yang dihasilkan sesuai dengan sifat yang diperhatikan, dan kemudian mengoptimumkan persamaan yang dilombong secara berulang. Oleh itu, isu teras penemuan pengetahuan automatik ialah perwakilan dan pengoptimuman.

Jadual 1. Jadual perbandingan kaedah perlombongan persamaan kawalan automatik
Cabaran untuk menyatakan masalah ialah: 1 . Cara menggunakan unit asas Terhingga untuk mewakili persamaan kawalan struktur kompleks tak terhingga (iaitu set calon terbuka) 2. Bagaimana untuk membina kaedah perwakilan persamaan kawalan yang mudah dikira. Untuk dapat menyatakan persamaan mana-mana struktur secara bebas, penyelidik melemahkan unit perwakilan asas SGA-PDE kepada operan dan operator, dan membina set calon terbuka menggunakan pepohon binari melalui matematik simbolik.
Cabaran masalah pengoptimuman ialah:1 Kecerunan antara bentuk persamaan dan indeks penilaian persamaan adalah sukar untuk dikira 2 set adalah tidak terhingga, dan proses pengoptimuman Sukar untuk mengimbangi penerokaan dan eksploitasi secara berkesan . Untuk mengoptimumkan masalah set calon terbuka dengan cekap, para penyelidik menggunakan algoritma genetik yang direka khas untuk struktur pokok untuk mencapai pengoptimuman dalam bentuk persamaan.
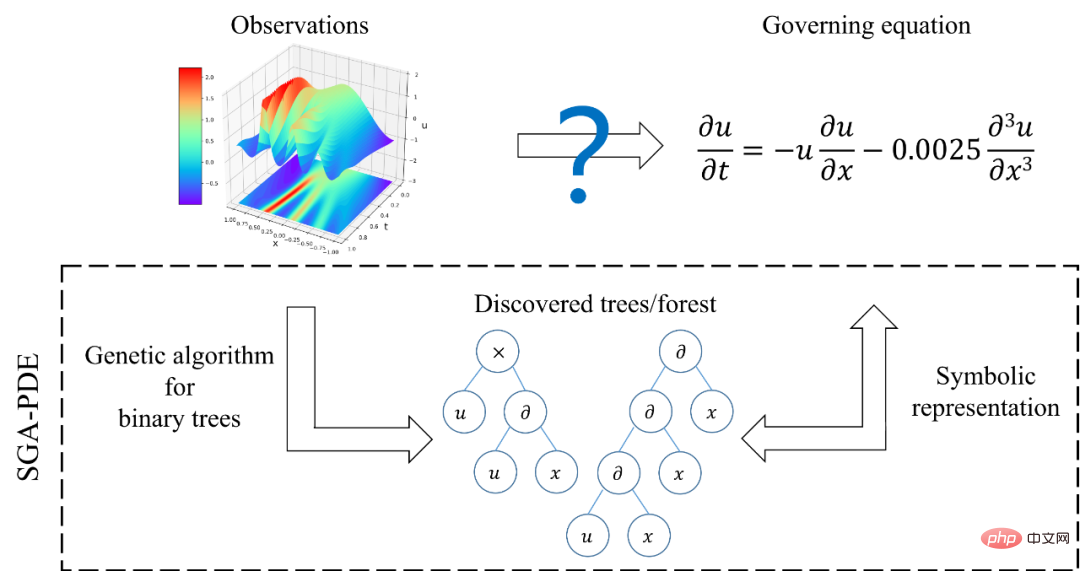
Penyelidik terlebih dahulu memperhalusi asas persamaan dalam unit Perwakilan algoritma untuk mewakili persamaan pembezaan separa bentuk terbuka,
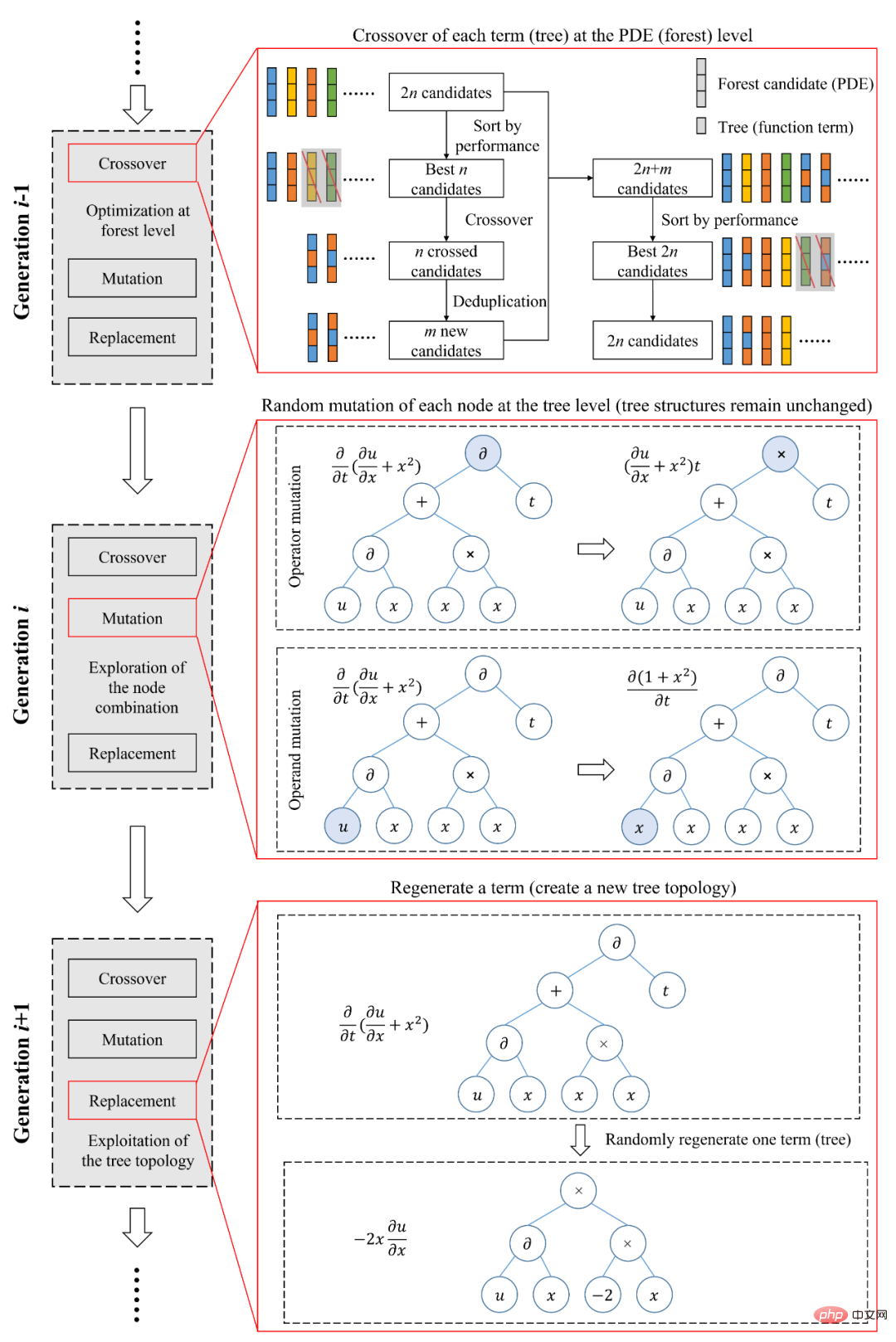
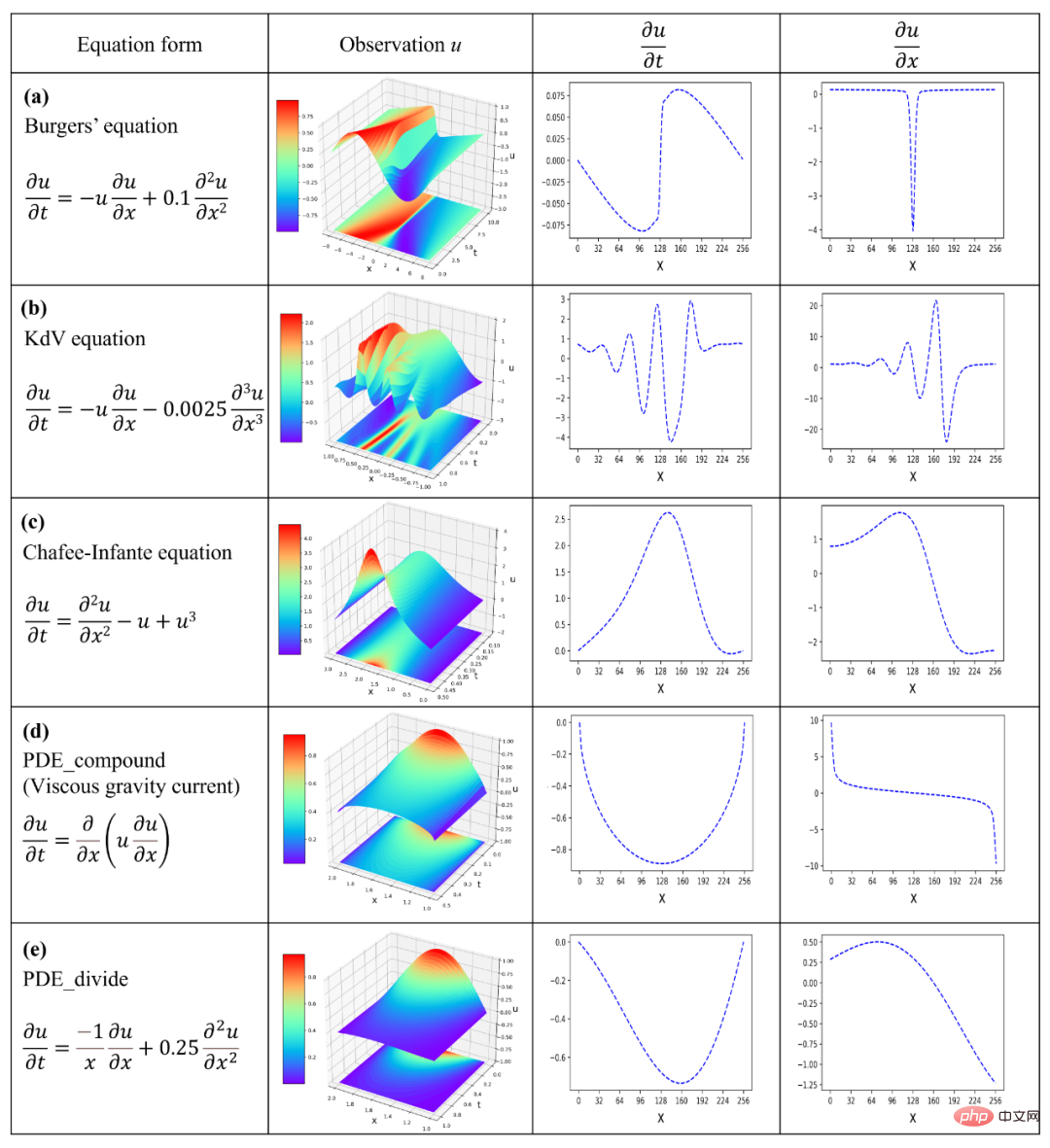
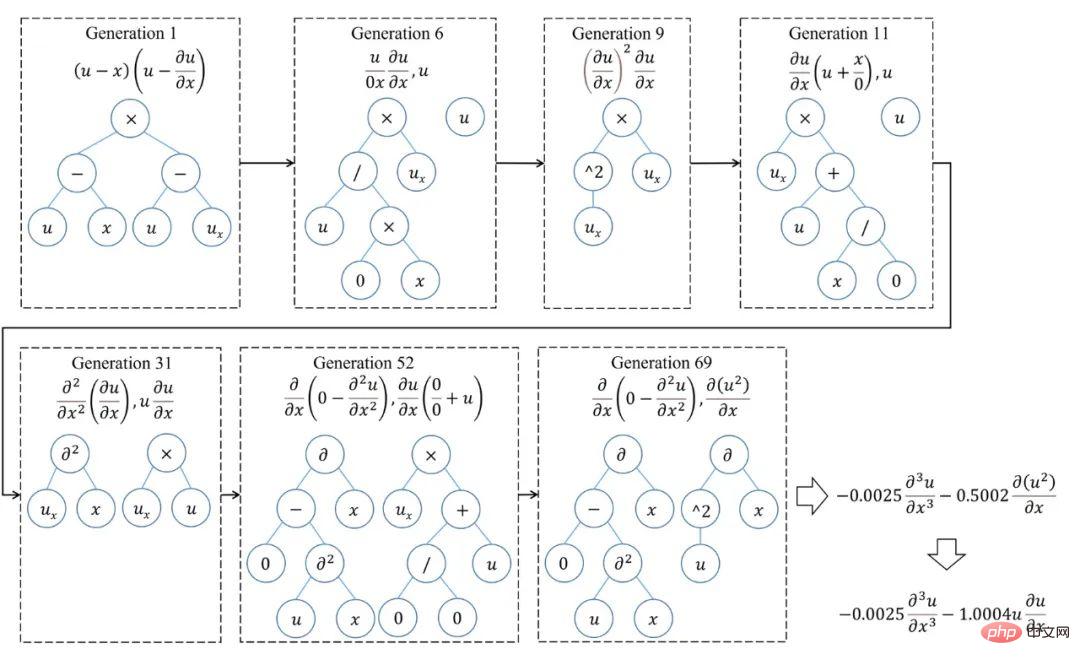
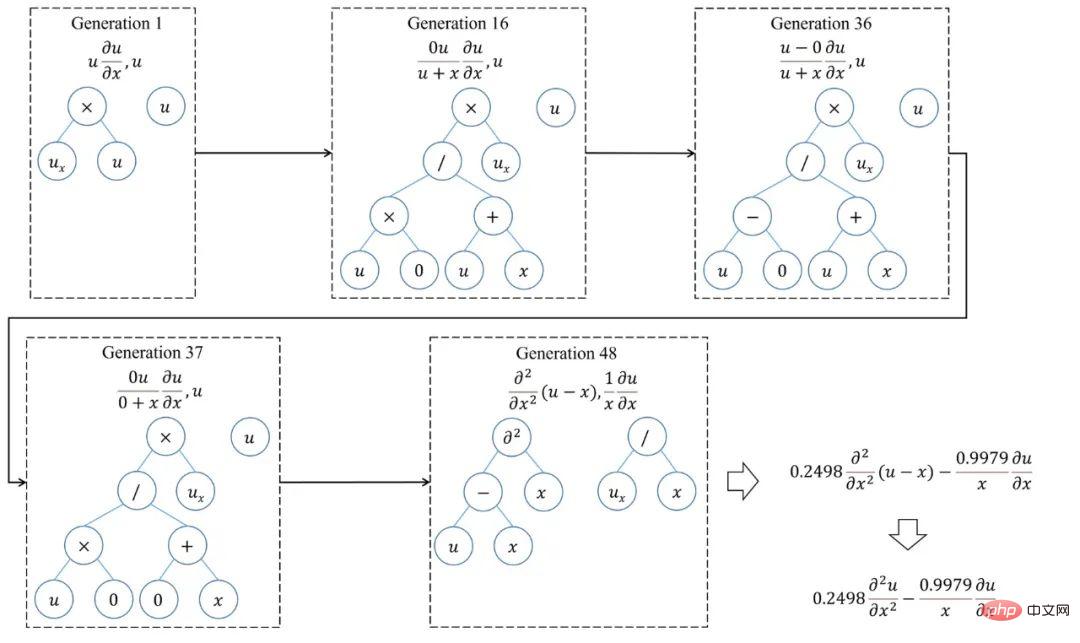
mengubah skala perwakilan persamaan daripada tahap sebutan fungsi bebas kepada tahap operator dan operan yang lebih asas. SGA-PDE membahagikan pengendali dalam persamaan kawalan kepada pengendali berganda (seperti +, -) dan pengendali tunggal (seperti sin, cos), dan kemudian mentakrifkan semua pembolehubah berpotensi sebagai operan (seperti x, t, u ). Penyelidik menggunakan struktur pokok binari untuk menggabungkan operator dan operan untuk mengekod persamaan yang berbeza. Semua nod terminal (nod daun dengan darjah 0) dalam pepohon binari sepadan dengan operan, dan semua nod bukan terminal sepadan dengan operator Double sepadan dengan nod dengan darjah 2, dan operator tunggal sepadan dengan nod dengan darjah 1. . Seperti yang ditunjukkan dalam Rajah 2, melalui rentetan yang boleh dikira sebagai sambungan, sebarang istilah fungsi boleh ditukar menjadi pepohon binari , dan pada masa yang sama, memenuhi peraturan matematik tertentu Pokok binari juga boleh ditukar kepada istilah fungsi . Tambahan pula, persamaan yang mengawal dengan istilah berbilang fungsi adalah bersamaan dengan hutan yang terdiri daripada berbilang pokok binari. SGA-PDE mewakili sebarang persamaan pembezaan separa bentuk terbuka melalui matematik simbolik. Selain itu, kertas kerja ini juga mencadangkan kaedah untuk menjana pokok binari secara rawak dengan makna matematik, yang dapat memastikan pokok binari yang dihasilkan tidak melanggar prinsip matematik. Rajah 2: Kaedah perwakilan dan transformasi antara pokok binari dan istilah fungsi Oleh kerana kaedah perwakilan yang ditunjukkan dalam Rajah 2 boleh Terdapat ialah surat-menyurat satu-dengan-satu antara sampel dalam ruang fungsi dan sampel dalam ruang pokok binari. Ini bermakna bahawa kaedah perwakilan berdasarkan matematik simbolik adalah cekap dan tidak berlebihan serta boleh digunakan sebagai proses pengekodan dalam algoritma genetik. Para penyelidik mencadangkan algoritma genetik untuk struktur pokok (Rajah 3) untuk melombong secara automatik persamaan kawalan yang konsisten dengan data pemerhatian daripada data eksperimen. Algoritma genetik untuk struktur pokok ini boleh mencapai pengoptimuman pada tahap yang berbeza . Pautan penyusunan semula adalah untuk mengoptimumkan di peringkat hutan (persamaan) untuk mencari gabungan optimum pokok binari (istilah fungsi). Pautan ini serupa dengan kaedah regresi jarang biasa semasa, iaitu pengoptimuman dalam set calon tertutup. Pautan mutasi dioptimumkan pada peringkat pokok binari (istilah fungsi) Dengan menjana atribut nod yang berbeza secara rawak, gabungan atribut nod yang optimum ditemui di bawah struktur pokok binari yang diberikan Ia adalah eksploitasi struktur semasa. Proses penggantian juga dioptimumkan pada peringkat pokok binari (istilah fungsi), tetapi ia akan menjana struktur pokok binari baharu, yang merupakan penerokaan struktur pokok dan mencapai sepenuhnya set calon terbuka. SGA-PDE boleh mengambil kira penggunaan dan penerokaan topologi pokok binari melalui pengoptimuman pelbagai peringkat, yang kondusif untuk mencari bentuk persamaan optimum dengan cekap. Rajah 3: Algoritma genetik untuk struktur pokok Data eksperimen ditunjukkan dalam Rajah 4, di mana lajur 2 menunjukkan Fizikal pemerhatian lapangan, ialah satu-satunya maklumat input SGA-PDE. Terbitan pertama yang mendasari dalam lajur 3 dan 4 boleh diperoleh dengan membezakan pemerhatian medan fizikal. Lajur 1 ialah bentuk persamaan yang betul. Dalam percubaan, SGA-PDE menggunakan operan dan pengendali pratetap yang sama, dan tidak perlu dilaraskan untuk masalah tertentu untuk mengesahkan kepelbagaian algoritma. Akhirnya, SGA-PDE berjaya melombong persamaan Burgers, persamaan KdV, persamaan Chafee-Infante, aliran graviti likat yang mengawal persamaan dengan terbitan fungsi komposit dan persamaan dengan struktur pecahan daripada data. Persamaan di atas mempunyai pelbagai bentuk kompleks seperti sebutan eksponen, sebutan terbitan peringkat tinggi, istilah interaksi, fungsi komposit dan struktur bersarang. Jadual 2 Keputusan eksperimen algoritma penemuan pengetahuan automatik dalam masalah perlombongan persamaan kawalan yang berbeza Untuk lebih memahami pencarian SGA- Proses Pengoptimuman PDE, Rajah 5 menunjukkan laluan evolusi apabila melombong persamaan KdV. Dapat dilihat bahawa persamaan optimum yang dihasilkan oleh generasi pertama adalah jauh daripada persamaan sebenar. Dalam proses evolusi seterusnya, dengan perubahan dalam struktur topologi pokok binari dan makna nod, serta penggabungan silang antara istilah fungsi, penyelesaian yang betul akhirnya ditemui dalam generasi ke-31, dan pada masa ini indeks AIC telah mencapai penumpuan yang diberikan dalam piawaian artikel. Menariknya, jika pengoptimuman diteruskan, ungkapan persamaan KdV yang lebih parsimoni berdasarkan terbitan fungsi komposit ditemui pada penjanaan 69. Rajah 6 menunjukkan proses pengoptimuman SGA-PDE untuk mencari persamaan yang mengawal dengan struktur pecahan. Rajah 5: Proses pengoptimuman persamaan KdV oleh SGA-PDE Rajah 6: Proses pengoptimuman SGA-PDE untuk persamaan dengan struktur pecahan Persamaan kawalan ialah perwakilan yang cekap bagi pengetahuan domain Walau bagaimanapun, parameter persamaan dan juga bentuk persamaan bagi banyak masalah kehidupan sebenar adalah Tidak Pasti , sukar untuk menulis persamaan kawalan yang tepat, yang sangat menyekat penggunaan pengetahuan domain dalam pembelajaran mesin. SGA-PDE mengubah persamaan melalui matematik simbolik dan menyelesaikan masalah perwakilan bentuk arbitrari persamaan pembezaan separa. Selain itu, SGA-PDE menggunakan algoritma genetik yang direka untuk pepohon binari, dan melalui pengoptimuman berulang topologi pepohon dan atribut nod, secara automatik melombong persamaan kawalan yang sesuai dengan data pemerhatian daripada domain terbuka. Dalam pengoptimuman, SGA-PDE tidak bergantung pada maklumat terdahulu dalam bentuk persamaan, dan juga tidak perlu diberikan set calon, mencapai pengoptimuman automatik bagi persamaan struktur kompleks . Pada masa yang sama, SGA-PDE juga merupakan algoritma bebas kecerunan, yang mengelakkan masalah pengiraan kecerunan yang sukar antara struktur persamaan dan nilai kerugian. Penyelidikan masa hadapan akan memberi tumpuan kepada: 1. Cuba menggabungkan pembelajaran pengukuhan atau algoritma pengoptimuman gabungan 2. Kurangkan ruang penyelesaian dengan membenamkan mekanisme fizikal; sifat data yang bising; 4. Mengintegrasikan kaedah pemasukan pengetahuan dan kaedah penemuan pengetahuan. Pautan kertas (tersedia secara percuma): https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.023174 Pautan data kod dan contoh : https://github.com/YuntianChen/SGA-PDE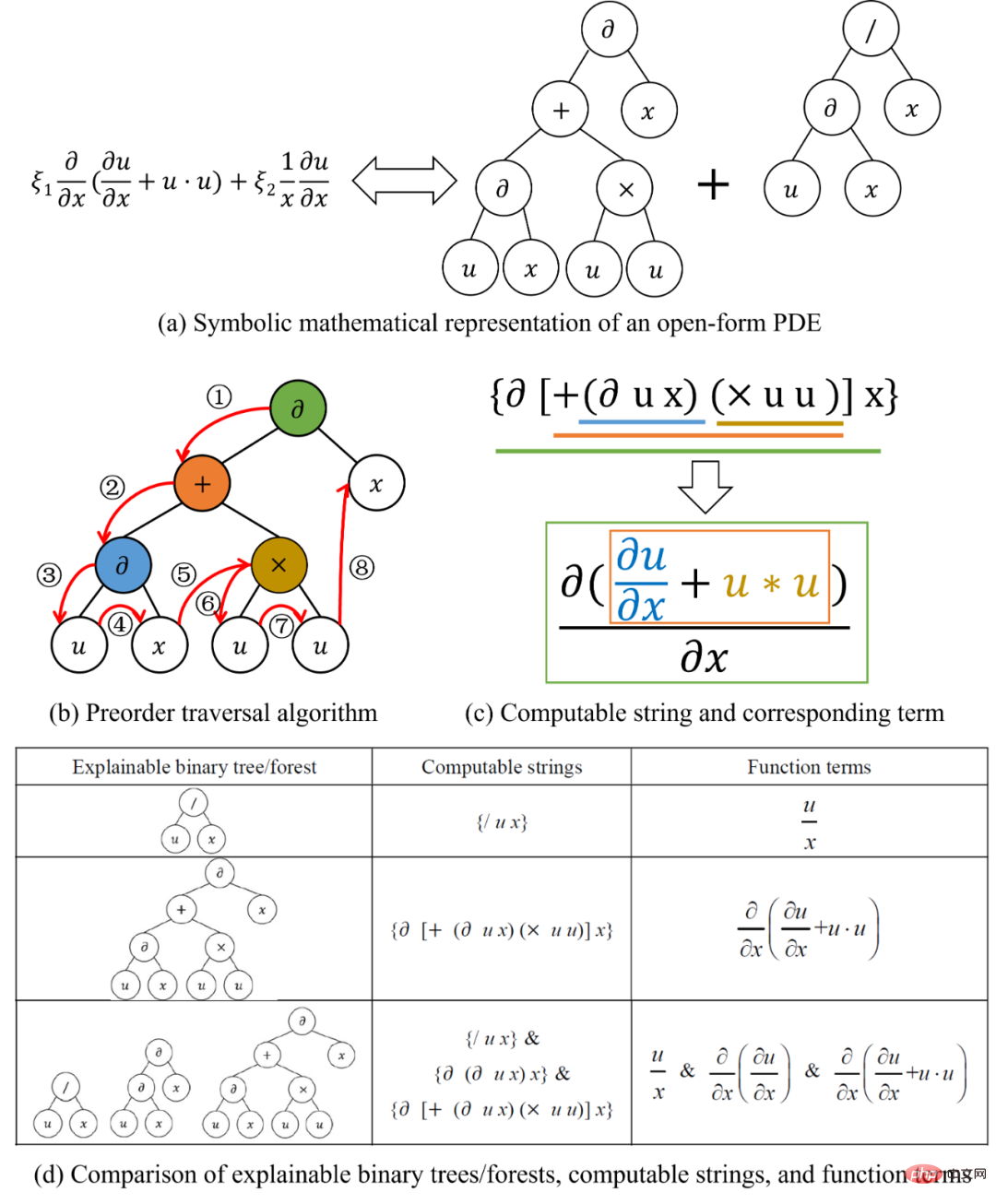

Atas ialah kandungan terperinci Adakah persamaan itu hutan pokok binari? Temui persamaan tadbir urus dan mekanisme fizikal yang tidak diketahui secara langsung daripada data. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

