Rumah >Peranti teknologi >AI >Penjelasan terperinci tentang teknologi perancangan keputusan pemanduan autonomi
Penjelasan terperinci tentang teknologi perancangan keputusan pemanduan autonomi
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-04 14:35:031902semak imbas
Dengan perkembangan pesat teknologi pembelajaran pengukuhan mendalam, semakin banyak pasukan penyelidik telah mula menerapkannya pada perancangan keputusan pemanduan autonomi, menyepadukan modul membuat keputusan tingkah laku dan perancangan gerakan untuk mempelajari trajektori pemanduan secara langsung.
Modul perancangan keputusan dalam pemanduan autonomi ialah salah satu petunjuk teras untuk mengukur dan menilai keupayaan pemanduan autonomi Tugas utamanya ialah menganalisis persekitaran semasa selepas menerima pelbagai maklumat deria daripada penderia, dan kemudian Mengeluarkan arahan kepada penderia. modul kawalan asas. Modul perancangan keputusan biasa boleh dibahagikan kepada tiga peringkat: perancangan laluan global, pembuatan keputusan tingkah laku dan perancangan gerakan.
01 Pengenalan
Dalam sistem pemanduan autonomi yang lengkap, jika modul persepsi dibandingkan dengan mata dan telinga manusia, maka perancangan membuat keputusan adalah otak pemanduan autonomi. Selepas menerima pelbagai maklumat deria daripada sensor, otak menganalisis persekitaran semasa dan kemudian mengeluarkan arahan kepada modul kawalan asas Proses ini adalah tugas utama modul membuat keputusan dan perancangan. Pada masa yang sama, betapa kompleksnya senario yang boleh dikendalikan oleh modul perancangan membuat keputusan juga merupakan salah satu petunjuk teras untuk mengukur dan menilai keupayaan pemanduan autonomi [1].
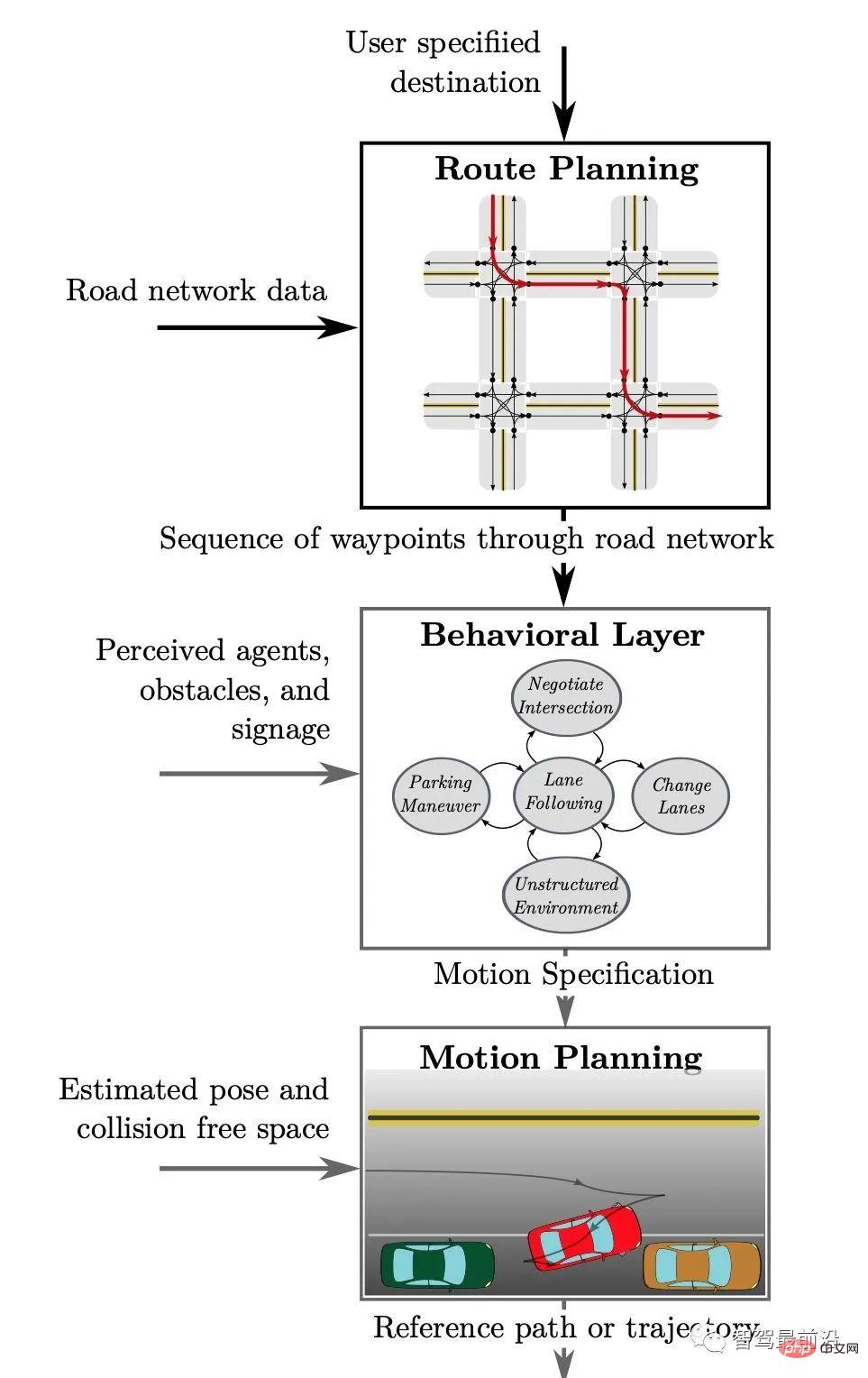
Rajah 1. Struktur hierarki modul perancangan keputusan dalam sistem pemanduan autonomi, dipetik daripada [2]
Seperti yang ditunjukkan dalam Rajah 1, a pembuatan keputusan biasa Modul perancangan boleh dibahagikan kepada tiga peringkat.
Antaranya, selepas menerima destinasi pemanduan yang diberikan, perancangan laluan global (Perancangan Laluan) menggabungkan maklumat peta untuk menjana laluan global sebagai rujukan untuk perancangan laluan khusus seterusnya
Selepas menerima laluan global, Lapisan Tingkah Laku menggabungkan maklumat persekitaran yang diperoleh daripada modul persepsi (termasuk kenderaan lain dan maklumat pejalan kaki, halangan dan peraturan lalu lintas di jalan raya) untuk membuat keputusan tingkah laku tertentu (seperti Pilih untuk menukar lorong untuk memotong atau mengikuti) ;
Akhir sekali, berdasarkan keputusan tingkah laku tertentu, lapisan Perancangan Pergerakan merancang untuk menjana laluan yang memenuhi kekangan tertentu (seperti kekangan dinamik kenderaan itu sendiri, pengelakan perlanggaran dan keselesaan penumpang, dsb .), yang digunakan sebagai input modul kawalan untuk menentukan laluan pemanduan terakhir kenderaan.
Artikel ini akan memperkenalkan fungsi utama dan algoritma biasa bagi setiap lapisan, dan membandingkan kelebihan dan kekurangan pelbagai algoritma dan senario yang berkenaan.
02 Perancangan laluan global (Perancangan Laluan)
Perancangan laluan global merujuk kepada pemilihan laluan optimum melalui carian selepas diberi kedudukan semasa kenderaan dan sasaran akhir "laluan optimum" di sini “Termasuk keadaan seperti laluan terpendek atau masa ketibaan terpantas. Proses ini adalah serupa dengan fungsi "navigasi" yang sering kita gunakan dalam kehidupan kita. Perbezaannya ialah peta berketepatan tinggi yang digunakan dalam pemanduan autonomi adalah berbeza daripada peta berketepatan tinggi kita mengandungi lebih banyak maklumat tentang setiap lorong maklumat. Algoritma perancangan laluan global yang biasa termasuk algoritma Dijkstra dan A, serta pelbagai penambahbaikan berdasarkan kedua-dua algoritma ini. Algoritma Dijkstra [3] dan algoritma A* [4] juga merupakan dua algoritma carian yang paling banyak digunakan dalam banyak masalah perancangan.
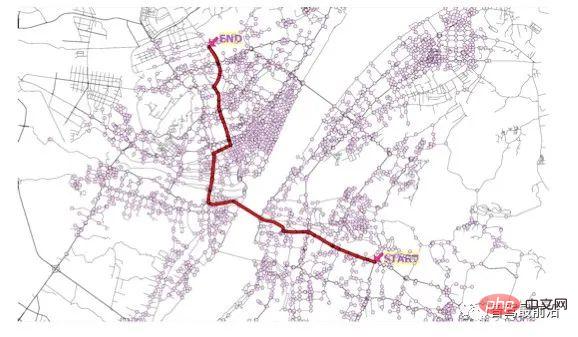
Rajah 2. Gambar rajah perancangan laluan global
1. saintis Edsger W. Dijkstra mencadangkannya pada tahun 1956 untuk mencari laluan terpendek antara nod dalam graf. Dalam algoritma Dijkstra, jumlah kos pergerakan setiap nod dari titik permulaan perlu dikira. Pada masa yang sama, struktur baris gilir keutamaan juga diperlukan. Semua nod yang akan dilalui akan diisih mengikut kos apabila diletakkan dalam barisan keutamaan. Semasa menjalankan algoritma, nod dengan kos terkecil dipilih daripada baris gilir keutamaan sebagai nod yang dilalui seterusnya setiap kali. sehingga anda sampai ke penghujung.
Kelebihan algoritma Dijkstra ialah laluan yang diberikan adalah optimum; kelemahannya ialah kerumitan masa pengiraan agak tinggi (O(N2)), kerana ia meneroka persekitaran tanpa arah yang jelas.2. Algoritma A*
Untuk menyelesaikan masalah kecekapan carian algoritma Dijkstra, pada tahun 1968, algoritma A telah dibangunkan oleh Peter Hart, Nils Nilsson dan Bertram Raphael dari Institut Penyelidikan Stanford Diterbitkan, penambahbaikan utamanya ialah menggunakan fungsi heuristik untuk membimbing proses carian. Secara khusus, Algoritma A mengira keutamaan setiap nod melalui fungsi berikut:
f(n)=g(n)+h(n)di mana:- f(n) ialah keutamaan menyeluruh nod n. Apabila kami memilih nod seterusnya untuk dilalui, kami sentiasa memilih nod dengan keutamaan keseluruhan tertinggi (nilai minimum).
- g(n) ialah kos nod n dari titik permulaan.
- h(n) ialah anggaran kos nod n dari titik akhir, iaitu fungsi heuristik bagi algoritma A*.
03 Lapisan Tingkah Laku
Selepas menentukan laluan global, kenderaan autonomi perlu membuat keputusan yang sesuai berdasarkan keadaan jalan tertentu, peraturan lalu lintas, kenderaan lain dan pejalan kaki, dsb. keputusan tingkah laku .
Proses ini menghadapi tiga masalah utama:
Pertama, adegan pemanduan sebenar sentiasa berubah, bagaimana untuk menutupnya?
Kedua, adegan pemanduan sebenar ialah persekitaran pembuat keputusan berbilang ejen Tingkah laku setiap peserta, termasuk kenderaan utama, akan memberi kesan kepada peserta lain dalam persekitaran, jadi kita Adalah perlu untuk. meramalkan tingkah laku peserta lain dalam persekitaran;
Akhir sekali, adalah mustahil untuk kenderaan autonomi mencapai 100% persepsi maklumat alam sekitar, contohnya, terdapat banyak kemungkinan situasi berbahaya yang disekat oleh halangan.
Berdasarkan perkara di atas, dalam lapisan membuat keputusan tingkah laku pemanduan autonomi, perkara yang perlu kita selesaikan ialah masalah perancangan ketidakpastian persepsi dalam persekitaran kompleks pembuatan keputusan berbilang ejen. Boleh dikatakan bahawa masalah ini adalah salah satu kesesakan teras dalam merealisasikan teknologi pemanduan autonomi tahap L4 dan L5 kebelakangan ini, dengan perkembangan pesat pembelajaran pengukuhan mendalam dan bidang lain, idea dan fajar baru telah dibawa untuk menyelesaikan masalah ini. masalah.
Model lapisan membuat keputusan tingkah laku berikut dibahagikan kepada empat kategori dan diperkenalkan masing-masing [5]:
1. Model mesin keadaan terhingga
Kenderaan pemanduan autonomi Model membuat keputusan awal ialah model mesin keadaan terhingga [6] Kenderaan memilih tingkah laku pemanduan yang sesuai mengikut persekitaran semasa, seperti tempat letak kereta, menukar lorong, memotong, mengelak, memandu perlahan, dsb. model mesin membina graf bersambung terarah terhingga Untuk menerangkan keadaan pemanduan yang berbeza dan hubungan peralihan antara keadaan, supaya secara reaktif menjana tindakan pemanduan berdasarkan peralihan keadaan pemanduan.
Model mesin keadaan terhingga kini merupakan model pembuatan keputusan tingkah laku yang paling meluas dalam bidang pemanduan autonomi kerana kesederhanaan dan kemudahan pelaksanaannya, bagaimanapun, model jenis ini mengabaikan dinamik dan ketidakpastian persekitaran Di samping itu, apabila ciri-ciri adegan pemanduan Dalam banyak kes, pembahagian dan pengurusan negeri adalah rumit, dan kebanyakannya sesuai untuk senario mudah, dan sukar untuk melaksanakan tugas membuat keputusan tingkah laku dalam persekitaran jalan bandar dengan ciri struktur yang kaya. .
2. Model pepohon keputusan
Model pepohon keputusan/kelakuan [7] adalah serupa dengan model mesin keadaan, dan juga secara reaktif memilih atribut yang berbeza melalui nilai atribut dari keadaan pemanduan semasa, tetapi perbezaannya ialah model jenis ini mengukuhkan status pemanduan dan logik kawalan ke dalam struktur pokok, dan mencari strategi pemanduan melalui mekanisme "pungutan suara" dari atas ke bawah. Model membuat keputusan jenis ini mempunyai logik kawalan visual, dan nod kawalan boleh digunakan semula, tetapi ia perlu mentakrifkan rangkaian membuat keputusan di luar talian untuk setiap senario pemanduan Apabila ruang keadaan dan ruang tingkah laku adalah besar, logik kawalan akan menjadi lebih kompleks. Selain itu, model jenis ini juga tidak dapat mempertimbangkan faktor ketidakpastian yang wujud dalam persekitaran trafik.
3. Model penaakulan dan pembuatan keputusan berasaskan pengetahuan
Model penaakulan dan pembuatan keputusan berasaskan pengetahuan meniru tingkah laku pemandu manusia dengan hubungan pemetaan "ciri adegan - tindakan memandu" Proses membuat keputusan, model jenis ini menyimpan pengetahuan pemanduan dalam pangkalan pengetahuan atau rangkaian saraf Pengetahuan memandu di sini terutamanya diwakili oleh hubungan pemetaan antara peraturan, kes atau ciri adegan dengan tindakan memandu. Kemudian, tindakan pemanduan disimpulkan daripada pangkalan pengetahuan atau struktur rangkaian terlatih melalui mekanisme "pertanyaan".
Model jenis ini terutamanya termasuk: sistem penaakulan berasaskan peraturan [8], sistem penaakulan berasaskan kes [9] dan model pemetaan berasaskan rangkaian saraf [10].
Model jenis ini sangat bergantung pada pengetahuan pemanduan dan data latihan terdahulu, dan memerlukan organisasi, pengurusan dan pengemaskinian pengetahuan pemanduan yang teliti Walaupun model pemetaan berdasarkan rangkaian saraf boleh menghapuskan keperluan untuk anotasi data dan pengetahuan proses penyepaduan, tetapi masih terdapat kekurangan berikut:
- Mekanisme yang dipacu "data" menjadikannya sangat bergantung pada data latihan, dan data latihan perlu mencukupi [11]; 🎜> Memantapkan hubungan pemetaan ke dalam struktur rangkaian mempunyai kebolehtafsiran yang lemah;
- mempunyai masalah "kotak hitam", ketelusan yang lemah, kebolehkesanan yang lemah bagi masalah yang berlaku dalam sistem sebenar, dan sukar untuk mencari punca punca masalah.
Menurut teori utiliti maksimum, idea asas keputusan berasaskan utiliti/nilai -membuat model adalah memilih pelbagai kriteria berdasarkan kriteria pemilihan Pilih strategi/tindakan pemanduan yang optimum antara alternatif [12].
Untuk menilai kualiti setiap tindakan pemanduan, model jenis ini mentakrifkan fungsi utiliti (utiliti) atau nilai (nilai) untuk menilai secara kuantitatif sejauh mana strategi pemanduan memenuhi objektif tugas pemanduan berdasarkan atribut kriteria tertentu Untuk tugas pemanduan tanpa pemandu, atribut kriteria ini boleh menjadi keselamatan, keselesaan, kecekapan pemanduan, dll. Utiliti dan nilai boleh ditentukan oleh satu atribut atau berbilang atribut.
Furda dan Vlacic dari Universiti Griffith di Australia mencadangkan kaedah membuat keputusan berbilang kriteria untuk memilih tindakan pemanduan yang optimum daripada set tindakan calon [13] dari Universiti Nasional Singapura yang dicadangkan membuat keputusan berdasarkan model POMDP [14] untuk menyelesaikan situasi di mana terdapat ketidakpastian yang dirasakan Wei J dan lain-lain dari Carnegie Mellon University mencadangkan model membuat keputusan tingkah laku [15] berdasarkan PCB (Berasaskan Ramalan dan-Kos-fungsi), yang memfokuskan Ia terletak pada bagaimana untuk membina fungsi kos yang sesuai untuk membimbing ramalan persekitaran untuk menyelesaikan masalah membuat keputusan dalam persekitaran yang kompleks yang melibatkan pelbagai agen, banyak model berdasarkan teori permainan juga digunakan oleh penyelidik untuk; sebab tentang interaksi antara kenderaan [16], [17] di samping itu, kerana kelebihannya dalam pengekstrakan ciri, teknologi pembelajaran tetulang mendalam juga telah mula digunakan secara meluas untuk melengkapkan penjanaan tindakan pemanduan yang optimum [18].
04 Perancangan Pergerakan
Selepas menentukan tingkah laku pemanduan khusus, apa yang perlu kita lakukan ialah mengubah "tingkah laku" itu menjadi "trajektori" pemanduan yang lebih spesifik supaya kita akhirnya boleh Menjana satu siri isyarat kawalan khusus untuk kenderaan mencapai pemanduan kenderaan mengikut sasaran yang dirancang. Proses ini dipanggil perancangan gerakan. Konsep perancangan gerakan mempunyai sejarah penyelidikan yang panjang dalam bidang robotik, kita boleh melihatnya sebagai masalah pengoptimuman berikut:
Perancangan Laluan.

Rajah 3. Definisi perancangan laluan
Dalam banyak senario yang diwakili oleh robot, Kita boleh menganggap persekitaran kita sebagai sesuatu yang pasti. Dalam kes ini, apa yang dipanggil perancangan laluan merujuk kepada mencari pemetaan σ:[0,1]➞Χ yang memenuhi kekangan tertentu dalam ruang keadaan tertentu Χ Kekangan ini termasuk:
- Tentukan keadaan permulaan dan kawasan di mana titik sasaran terletak
- Elakkan perlanggaran
- Kekangan berbeza pada laluan (contohnya, dalam masalah sebenar, kelengkungan laluan tidak boleh terlalu kecil, sepadan dengan yang kedua Tertib Kekangan pada terbitan)
Kefungsian objektif masalah pengoptimuman ini ditakrifkan sebagai J(σ), dan makna khususnya boleh dinyatakan sebagai panjang laluan, kerumitan kawalan dan ukuran lain.
Namun, dalam masalah pemanduan automatik, persekitaran di sekeliling kenderaan sentiasa berubah secara dinamik, jadi perancangan laluan yang mudah tidak dapat memberikan penyelesaian yang sentiasa sah semasa proses pemanduan, jadi kita perlu menambah dimensi - masa T , masalah perancangan yang sepadan biasanya dipanggil perancangan trajektori.
Perancangan Trajektori

Rajah 4. Definisi Perancangan Trajektori
Peningkatan dimensi masa menimbulkan cabaran yang besar kepada isu perancangan. Sebagai contoh, untuk robot yang bergerak dalam persekitaran 2D, yang diabstraksi sebagai satu titik, halangan dalam persekitaran dianggarkan sebagai poligon. Masalah perancangan laluan boleh diselesaikan dalam masa polinomial, manakala masalah perancangan trajektori yang menambah dimensi masa telah terbukti sebagai masalah NP-hard.
Dalam senario sebenar pemanduan autonomi, sama ada kenderaan itu sendiri atau persekitaran sekeliling, mewujudkan model yang lebih tepat bermakna kekangan yang lebih kompleks terhadap masalah pengoptimuman, dan ini juga bermakna penyelesaiannya lebih sukar. Oleh itu, algoritma yang sebenarnya digunakan adalah berdasarkan premis penghampiran adegan sebenar, dan mencari keseimbangan optimum antara ketepatan model dan kecekapan penyelesaian.
Berikut memperkenalkan beberapa jenis algoritma perancangan gerakan pada masa ini biasa dalam bidang pemanduan autonomi Dalam amalan, selalunya gabungan beberapa jenis idea yang akhirnya boleh mencapai hasil perancangan yang lebih baik dan memenuhi keperluan yang lebih berbeza. tempat kejadian.
1. Algoritma perancangan berasaskan carian
Menyelesaikan masalah perancangan gerakan melalui carian adalah salah satu idea yang paling mudah adalah untuk melepasi ruang keadaan yang ditentukan Kaedah ini didiskrisikan ke dalam graf, dan kemudian pelbagai algoritma carian heuristik digunakan untuk mencari penyelesaian yang boleh dilaksanakan atau penyelesaian yang optimum.
Dalam proses mendiskrisikan ruang keadaan, perhatian harus diberikan untuk memastikan bahawa grid akhir mempunyai kawasan liputan terbesar dan tidak berulang. Seperti yang ditunjukkan dalam Rajah 5, grid di sebelah kiri dijana oleh tiga gelagat: pergi lurus, belok kiri 90°, dan belok kanan 90° dan jika anda memilih tiga gelagat: pergi lurus, belok kiri 89° dan belok kanan 89; °, anda tidak akan dapat Menjana struktur grid meliputi seluruh kawasan.
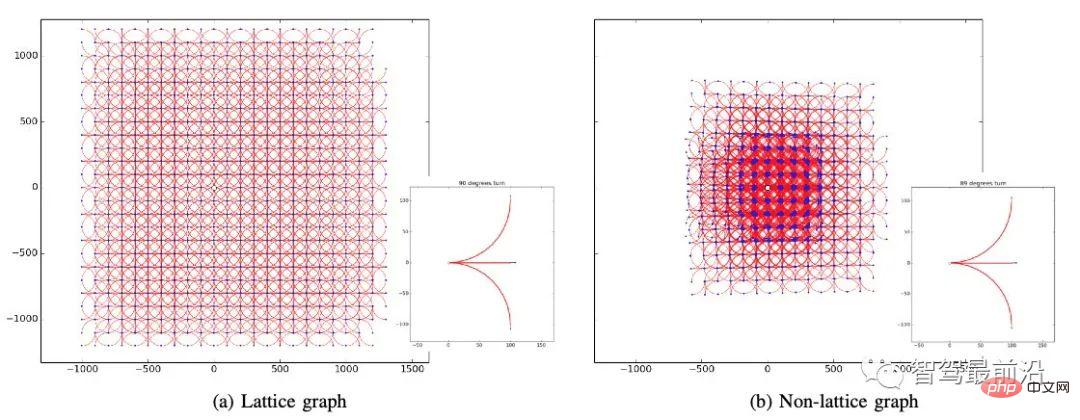
Rajah 5. Membina graf raster, dipetik daripada [2]
Selepas rasterisasi ruang keadaan, kita boleh menggunakan Dijkstra, yang telah diperkenalkan sebelum ini, A* algoritma carian untuk melengkapkan perancangan akhir. Walau bagaimanapun, dalam persekitaran kompleks sebenar, terdapat banyak grid dan persekitaran berubah secara dinamik dari semasa ke semasa, yang akan membawa kepada terlalu banyak nod carian Oleh itu, pelbagai algoritma yang dipertingkatkan telah dibangunkan untuk menangani senario khusus yang berbeza:
1) Algoritma Hibrid A*, berdasarkan algoritma A*, mempertimbangkan masalah stereng maksimum kenderaan Sebagai contoh, arah stereng maksimum kenderaan pada laluan yang dikira adalah terhad kepada tidak lebih daripada 5°. Senario aplikasi semasa algoritma ini termasuk pusingan U kereta (kereta Junior yang digunakan oleh Stanford untuk mengambil bahagian dalam cabaran DARPA menggunakan algoritma ini untuk melaksanakan uturn), tempat letak kereta dan senario lain yang memerlukan kawalan stereng yang tinggi. 2) Algoritma D*, D*Lite, cari dari titik akhir ke titik permulaan terlebih dahulu, gunakan algoritma Dijkstra, simpan panjang laluan terpendek k dari titik sasaran ke setiap titik dalam rangkaian jalan raya, dan nod ke titik sasaran Nilai panjang sebenar h, dalam kes awal k==h, dan nod sebelumnya setiap nod disimpan untuk memastikan pautan boleh diikuti. Selepas pengiraan, laluan optimum pada masa itu diperolehi. Apabila kereta bergerak ke nod tertentu dan mendapati bahawa nod tidak boleh dilalui (terdapat halangan) melalui sensor, nilai h beberapa titik yang berkaitan dalam maklumat rangkaian jalan yang disimpan diubah suai (meningkat), dan titik jiran dipilih yang masih memenuhi masalah h==k, iaitu titik pada laluan optimum masih merupakan titik seterusnya. Kemudian berjalan ke penghujung. Algoritma jenis ini sesuai untuk navigasi dan perancangan laluan dalam persekitaran yang tidak diketahui, dan digunakan secara meluas dalam pelbagai robot mudah alih semasa dan kenderaan autonomi, seperti "Peluang" dan "Spirit" Mars rover.2. Algoritma perancangan berasaskan persampelan
Dengan mengambil sampel ruang keadaan berterusan, masalah asal dianggarkan kepada masalah pengoptimuman jujukan diskret. Ia juga adalah algoritma yang paling banyak digunakan dalam sains komputer. Dalam masalah perancangan gerakan, algoritma berasaskan persampelan asas termasuk algoritma Pelan Hala Tuju Probabilistik (PRM) dan Rapid Search Random Tree (RRT).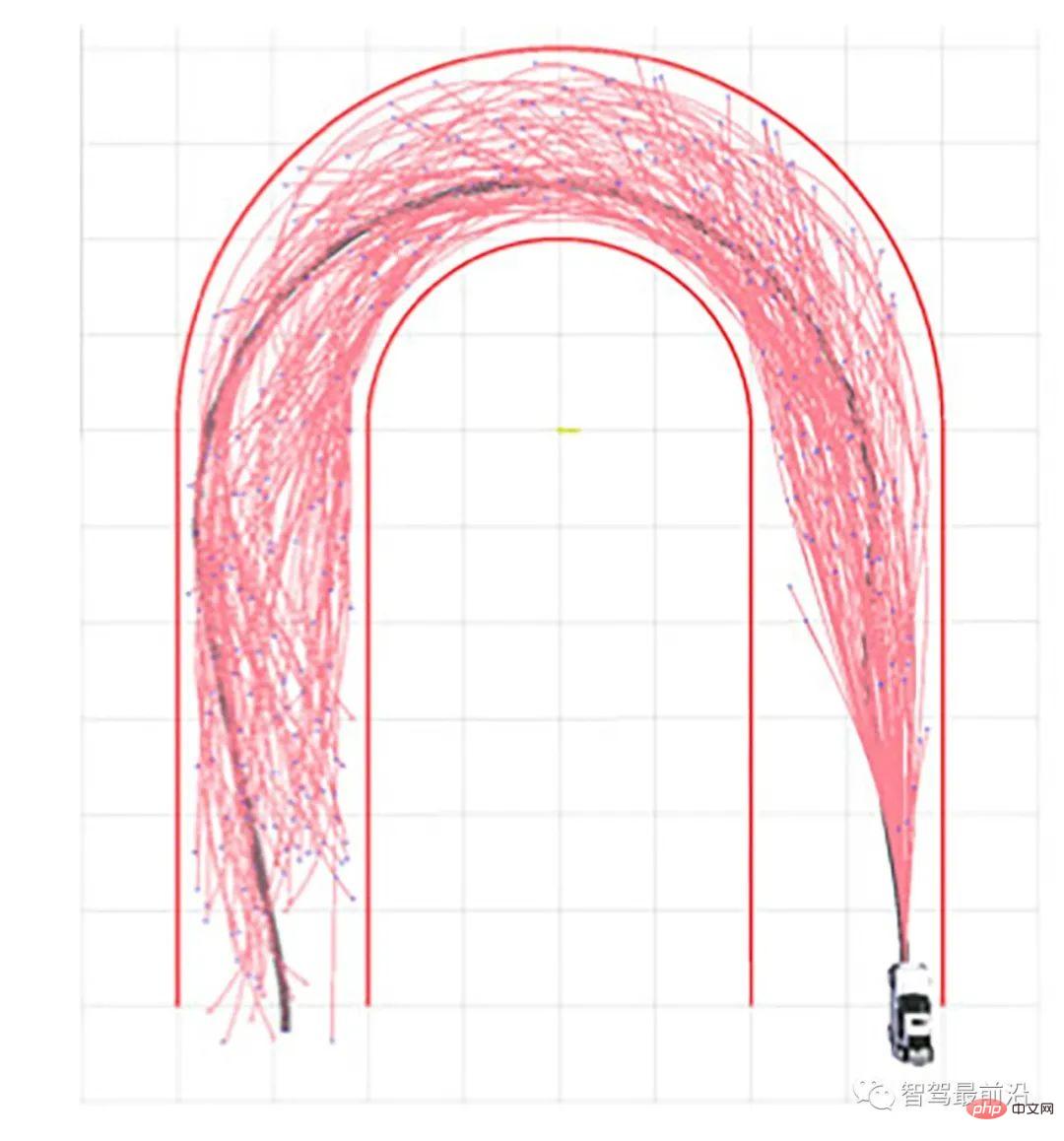
1) Algoritma asas: laluan probabilistik Rajah (PRM)
- Peringkat prapemprosesan: sampel n titik secara seragam dan rawak di kawasan selamat dalam ruang keadaan, dan setiap titik pensampelan disambungkan ke titik pensampelan bersebelahan dalam jarak tertentu . Sambung, dan buang trajektori yang bertembung dengan halangan, dan akhirnya dapatkan graf yang disambungkan.
- Fasa pertanyaan: Untuk pasangan keadaan awal dan sasaran tertentu, sambungkannya kepada graf yang telah dibina, kemudian gunakan algoritma carian untuk mencari trajektori yang memenuhi keperluan.
2) Algoritma asas: Rapid Search Random Tree (RRT)
- Permulaan pepohon: Mulakan set nod dan set tepi pepohon, set nod Hanya mengandungi keadaan awal, dan set tepi kosong.
- Pertumbuhan pokok: Sampel ruang keadaan secara rawak Apabila titik pensampelan jatuh di kawasan selamat ruang keadaan, pilih nod yang paling hampir dengan titik pensampelan dalam pokok semasa dan kembangkan (atau sambungkan)nya. ke titik persampelan. Jika trajektori yang dijana tidak bertembung dengan halangan, trajektori ditambah pada set tepi pokok, dan titik akhir trajektori ditambah pada set nod pokok.
3) Pelbagai algoritma yang dipertingkatkan
Daripada penerangan algoritma asas di atas, kita dapat memahami bahawa pensampelan ruang keadaan boleh memastikan bahawa titik permulaan dan titik akhir disambungkan penyelesaian yang optimum. Sebagai tindak balas kepada kelemahan ini, pelbagai algoritma yang dipertingkatkan telah dicadangkan dan digunakan untuk masalah pemanduan autonomi:- Peningkatan kecekapan--pensampelan tidak sekata
- Digabungkan dengan model pemandu: Digabungkan dengan model perhatian visual pemandu untuk pensampelan berat sebelah, menggunakan maklumat ciri visual untuk membimbing perancangan gerakan, supaya trajektori yang dirancang lebih konsisten dengan tingkah laku pemanduan manusia.
- Bina RG-RRT metrik baharu (RT berpandukan kebolehcapaian): metrik jarak Euclidean konvensional tidak boleh benar-benar mencerminkan jarak antara konfigurasi atau keadaan RG-RRT mengira set kebolehcapaian nod dalam pepohon , apabila jarak dari titik pensampelan ke nod adalah lebih besar daripada jarak dari titik pensampelan ke set nod yang boleh dicapai, nod boleh dipilih untuk pengembangan.
- Tambah penalti halangan (RC-RRT, EG-RRT, ADD-RRT, dll.): Kurangkan kebarangkalian bahawa nod yang hampir dengan halangan akan dikembangkan.
- Peningkatan masa nyata
- bila-bila masa RRT mula-mula cepat membina RRT, memperoleh penyelesaian yang boleh dilaksanakan dan merekodkan kosnya Selepas itu, algoritma akan meneruskan pensampelan, tetapi ia hanya akan memanfaatkan Nod yang mengurangkan kos penyelesaian yang boleh dilaksanakan dimasukkan ke dalam pokok, dengan itu secara beransur-ansur memperoleh penyelesaian yang boleh dilaksanakan yang lebih baik.
- Perancangan semula menguraikan keseluruhan tugasan perancangan kepada beberapa urutan subtugasan pada masa yang sama dan merancang tugas seterusnya sambil melaksanakan tugasan semasa.
- Peningkatan keoptimuman
- PRM*, RRG, RRT*: Mengikut teori graf geometri rawak (sampel m titik secara rawak dalam ruang keadaan, dan bahagikan jarak Mata lebih kecil daripada r(n) disambungkan untuk membentuk graf geometri rawak) PRM standard dan RRT ditambah baik, dan algoritma PRM*, RRG dan RRT* dengan sifat optimum tanpa gejala diperoleh
3. Kaedah pengoptimuman langsung
Dalam kebanyakan kes, tanpa mengira perubahan ketinggian, masalah perancangan trajektori pemanduan autonomi ialah masalah pengoptimuman terkekang tiga dimensi (ruang 2D + masa T), jadi , kita boleh menggunakan strategi decoupling untuk menguraikan masalah asal kepada beberapa masalah berdimensi rendah, sekali gus mengurangkan kesukaran untuk menyelesaikannya.
1) Sistem koordinat Frenet
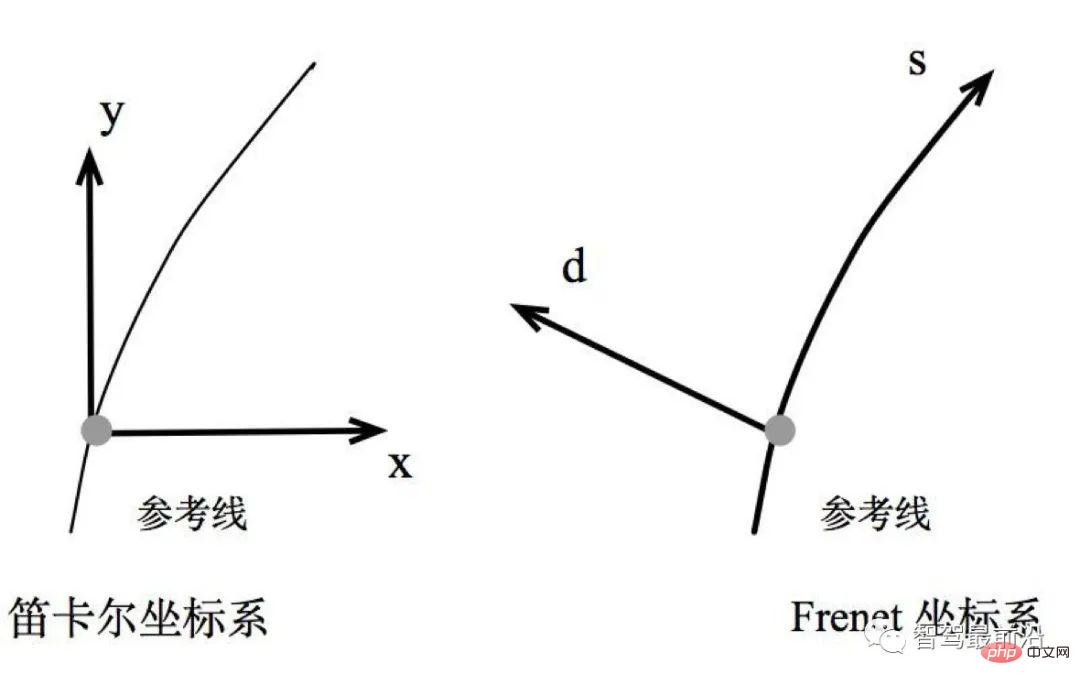
Rajah 7. Sistem koordinat Frenet
Disebabkan oleh dunia nyata Jalan raya di dalamnya semuanya melengkung Untuk memudahkan ungkapan parameter untuk menyelesaikan masalah pengoptimuman, sistem koordinat Frenet biasanya digunakan dalam pemanduan autonomi.
Dalam sistem koordinat Frenet, kami menggunakan garis tengah jalan sebagai garis rujukan, dan menggunakan vektor tangen t dan vektor normal n garis rujukan untuk mewujudkan sistem koordinat, seperti yang ditunjukkan dalam rajah di sebelah kanan, yang mengambil kenderaan itu sendiri sebagai Asal, paksi koordinat berserenjang antara satu sama lain, dibahagikan kepada arah s (iaitu, arah sepanjang garis rujukan, sering dipanggil membujur, Membujur) dan arah d (atau Arah L, iaitu, arah normal semasa garis rujukan, dipanggil mendatar, Lateral ), berbanding sistem koordinat Cartesian (gambar kiri), sistem koordinat Frenet memudahkan masalah dengan ketara.
Oleh kerana apabila memandu di jalan raya, kita sentiasa mudah mencari garis rujukan jalan (iaitu, garis tengah jalan), maka kedudukan berdasarkan garis rujukan boleh dinyatakan dengan mudah menggunakan garis membujur jarak S (iaitu, sepanjang Ia diterangkan dengan jarak sepanjang arah jalan) dan jarak sisi L (iaitu jarak jauh dari garis rujukan).
2) Kaedah penyahgandingan kelajuan laluan
Dalam sistem koordinat Frenet, kaedah penyahgandingan kelajuan laluan masing-masing mengoptimumkan laluan dan kelajuan Memandangkan halangan statik, laluan rujukan statik (dimensi SL) dijana melalui perancangan dinamik, dan kemudian berdasarkan laluan yang dijana, perancangan kelajuan (dimensi ST) dipertimbangkan. Proses ini boleh diulang secara berterusan, membolehkan kemas kini masa nyata pada trajektori. Perancang EM yang digunakan dalam platform pemanduan autonomi sumber terbuka Baidu Apollo adalah berdasarkan penyelesaian yang serupa. Penyelesaian ini mempunyai fleksibiliti yang kuat dan boleh digunakan secara universal pada banyak senario.
Selain itu, anda juga boleh memilih kaedah penyahgandingan yang berbeza, seperti merancang trajektori longitudinal (dimensi ST) dan trajektori melintang (dimensi LT) secara berasingan. Walau bagaimanapun, perlu ditegaskan bahawa penyelesaian yang diperoleh melalui kaedah penyahgandingan mungkin tidak optimum, dan algoritma ini tidak lengkap, dan penyelesaian yang boleh dilaksanakan mungkin tidak ditemui dalam beberapa persekitaran yang kompleks.
4. Kaedah pembinaan lengkung parametrik
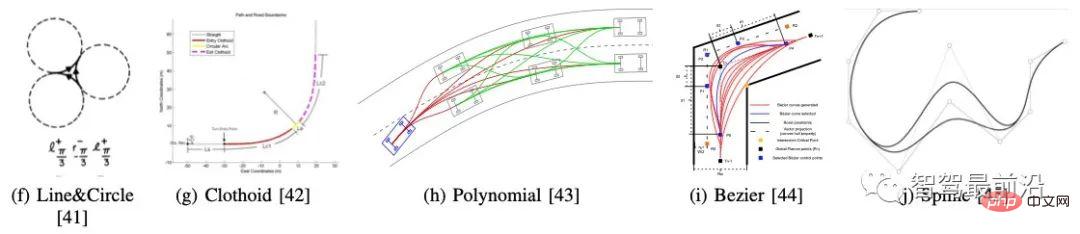
Rajah 8. Kaedah pembinaan lengkung parametrik biasa, dipetik daripada [19]
Titik permulaan kaedah pembinaan lengkung parametrik adalah kekangan kenderaan itu sendiri, termasuk kekangan kinematik dan dinamik Oleh itu, laluan yang dirancang secara amnya perlu mempunyai kelengkungan berterusan. Kaedah jenis ini mempertimbangkan halangan berdasarkan titik permulaan dan titik sasaran, dan memberikan laluan yang lancar dengan membina sekumpulan lengkung yang mematuhi kekangan kenderaan.
Seperti yang ditunjukkan dalam Rajah 8, lengkung biasa termasuk lengkung Dubins (terdiri daripada garis lurus dan lengkok, yang merupakan keluarga lengkung terpendek bagi model kenderaan ringkas model Dubin dalam ruang dua dimensi), lengkung clothoid dan polinomial lengkung , lengkung Bezier, lengkung spline, dsb. Sukar untuk hanya menggunakan kaedah pembinaan lengkung parametrik untuk memenuhi senario kompleks sebenar Oleh itu, semakin banyak sistem pemanduan autonomi kini menggabungkannya dengan kaedah lain untuk melicinkan trajektori yang dirancang dan dijana untuk memenuhi kekangan dan dinamik kenderaan.
5. Kaedah medan potensi buatan
Kaedah medan potensi buatan diilhamkan oleh medan elektromagnet dalam fizik Diandaikan bahawa halangan dan kedudukan sasaran masing-masing menghasilkan tolakan dan graviti, supaya laluan boleh dirancang di sepanjang penurunan kecerunan terpantas medan potensi. Isu utama dalam kaedah jenis ini ialah cara memilih fungsi medan berpotensi yang sesuai Contohnya, Stephen Waydo menggunakan fungsi aliran untuk perancangan laluan lancar [20], dan Robert Daily mencadangkan kaedah perancangan laluan medan berpotensi harmonik pada kenderaan berkelajuan tinggi. [21]. Dalam senario mudah, kaedah medan potensi buatan mempunyai kecekapan penyelesaian yang tinggi, tetapi masalah terbesarnya ialah ia mungkin jatuh ke dalam minimum tempatan Dalam kes ini, laluan yang diperolehi tidak optimum, dan laluan itu mungkin tidak dijumpai.
05 Algoritma Kerumitan (Kerumitan)
Dalam merancang masalah, selain mempertimbangkan masa dan kerumitan ruangnya, penilaian algoritma juga mesti mempertimbangkan sama ada ia mempunyai kesempurnaan dan Optimal, mengambil langkah kembali dan pertimbangkan sama ada ia mempunyai kesempurnaan kebarangkalian dan optimum tanpa gejala. Hanya berdasarkan pemahaman sifat ini, kami boleh mereka bentuk dan menggunakan algoritma yang berbeza untuk senario sebenar yang berbeza, untuk mencapai keseimbangan terbaik antara kerumitan model dan kecekapan optimum.
1) Kelengkapan: Jika terdapat penyelesaian laluan antara titik permulaan dan titik sasaran, maka penyelesaian itu mesti diperolehi, ia bermakna tiada penyelesaian; >
2) Kesempurnaan Secara Kebarangkalian: Jika terdapat penyelesaian laluan antara titik permulaan dan titik sasaran, selagi perancangan atau masa carian cukup lama, anda pasti akan menemui penyelesaian laluan 3) Keoptimuman: Laluan yang dirancang adalah optimum pada indeks penilaian tertentu (indeks penilaian secara amnya ialah panjang laluan) 4) Keoptimuman tanpa gejala: selepas nombor terhingga Laluan yang diperoleh selepas lelaran perancangan ialah laluan suboptimum yang hampir kepada optimum, dan ia lebih dekat dengan laluan optimum selepas setiap lelaran Ia adalah proses penumpuan secara beransur-ansur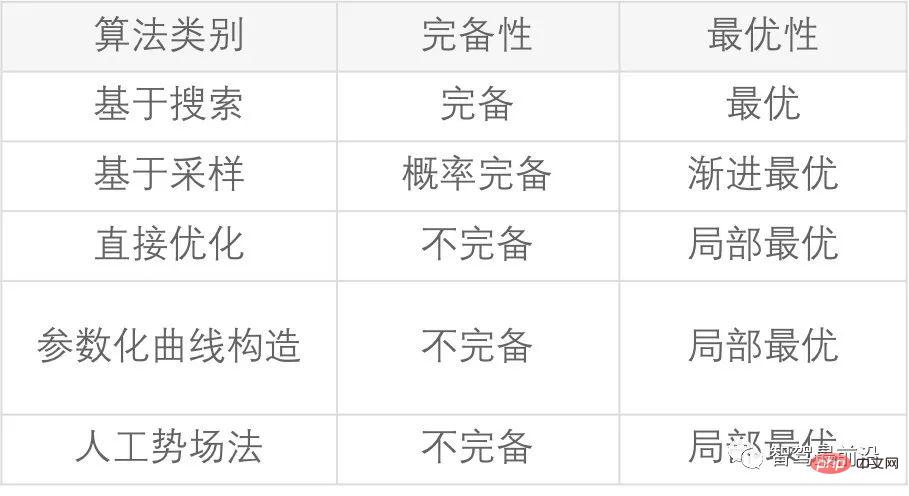
- Model hujung-ke-hujung: Gunakan rangkaian saraf dalam untuk mendapatkan terus isyarat kawalan kenderaan berdasarkan status kenderaan dan maklumat persekitaran luaran. Walaupun model hujung-ke-hujung semasa tidak dapat ditafsirkan seperti "kotak hitam", adalah dipercayai bahawa apabila manusia terus mendalami pemahaman mereka tentang rangkaian saraf dalam, kaedah ini mempunyai potensi pembangunan yang kukuh kerana kelebihan kesederhanaan dan kecekapannya yang luar biasa.
- Integrasi modul membuat keputusan dan perancangan gerakan
- Kenderaan autonomi membuat keputusan yang optimum dalam persekitaran yang kompleks Masalah ini sangat konsisten dengan definisi pembelajaran pengukuhan, seperti yang dinyatakan di atas Dengan perkembangan pesat teknologi pembelajaran pengukuhan, semakin ramai pasukan penyelidik telah mula menerapkannya pada perancangan keputusan pemanduan autonomi, menyepadukan pembuatan keputusan tingkah laku dengan modul perancangan gerakan untuk mempelajari trajektori pemanduan secara langsung. Bagi menyelesaikan masalah bahawa fungsi ganjaran persekitaran tidak mudah diperoleh, ia juga telah dicadangkan untuk menggunakan pembelajaran peneguhan songsang (IRL) terlebih dahulu untuk belajar berdasarkan demonstrasi pakar manusia, dan kemudian menggunakan pembelajaran peneguhan untuk mempelajari dasar yang optimum.
Atas ialah kandungan terperinci Penjelasan terperinci tentang teknologi perancangan keputusan pemanduan autonomi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

