Fahami secara ringkas idea asas dan pelaksanaan dikotomi di Jawa

Artikel ini membawakan anda pengetahuan yang berkaitan tentang java Kaedah pembahagian dua ialah algoritma yang sangat cekap, yang sering digunakan dalam proses carian komputer. Berikut akan menerangkan idea asas dan pelaksanaan dikotomi secara terperinci melalui contoh-contoh saya harap ia akan membantu semua orang.

Pembelajaran yang disyorkan: "tutorial video java"

Dalam tatasusunan tertib, cari sama ada nombor tertentu wujud

Idea:

• Memandangkan ia adalah tatasusunan tertib, anda boleh mendapatkan kedudukan titik tengah dahulu, dan titik tengah boleh membahagi tatasusunan kepada separuh kiri dan kanan.
• Jika nilai kedudukan titik tengah adalah sama dengan nilai sasaran, kembalikan kedudukan titik tengah secara langsung.
• Jika nilai kedudukan titik tengah kurang daripada nilai sasaran, pergi ke sebelah kiri titik tengah tatasusunan dan cari dengan cara yang sama.
• Jika nilai kedudukan titik tengah lebih besar daripada nilai sasaran, ambil bahagian kanan titik tengah tatasusunan dan cari dengan cara yang sama.
• Jika tidak ditemui pada akhirnya, kembalikan: -1.

Kod

class Solution {
    public int search(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
                return m;
            } else if (arr[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

Kerumitan masa O(logN).

Dalam tatasusunan tertib, cari kedudukan paling kiri yang lebih besar daripada atau sama dengan nombor tertentu

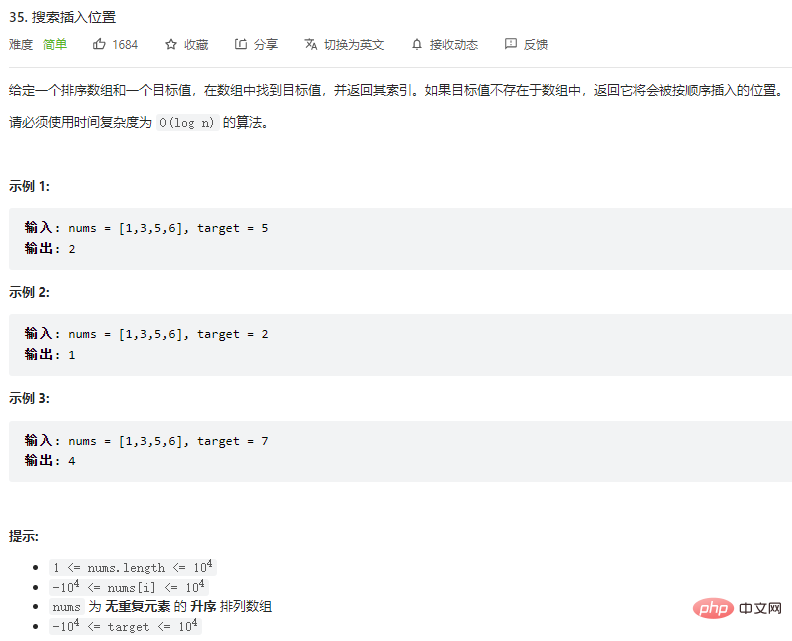
Contoh 1:

Input : nums = [1,3,5,6], target = 5

Output: 2

Penjelasan: Jika anda ingin memasukkan elemen 5 ke dalam tatasusunan num, ia sepatutnya disisipkan pada Kedudukan antara elemen 3 dan elemen 5, iaitu kedudukan No. 2.

Contoh 2:

Input: nums = [1,3,5,6], sasaran = 2

Output: 1

Penjelasan: Jika Untuk memasukkan elemen 2 ke dalam tatasusunan num, ia hendaklah dimasukkan pada kedudukan antara elemen 1 dan elemen 3, iaitu kedudukan 1.

Contoh 3:

Input: nums = [1,3,5,6], sasaran = 7

Output: 4

Penjelasan: Jika Untuk memasukkan elemen 7 ke dalam tatasusunan num, ia hendaklah dimasukkan pada penghujung tatasusunan, iaitu pada kedudukan 4.

Seperti yang anda boleh ketahui daripada contoh di atas, soalan ini pada dasarnya bertanyaDalam tatasusunan tertib, cari kedudukan paling kiri yang lebih besar daripada atau sama dengan nombor tertentu Jika tidak wujud, kembali panjang tatasusunan (mewakili Sisipkan di hujung sekali)

Kita hanya perlu membuat perubahan mudah berdasarkan contoh di atas, apabila kita mendapati kedudukan yang memenuhi syarat, kita boleh terus return

if (arr[m] == t) {
    return m;
}

Dalam soalan ini, kerana kita perlu mencari kedudukan paling kiri, apabila menemui kesamaan, kita hanya perlu merekodkan kedudukan terlebih dahulu tanpa kembali terus, dan kemudian teruskan ke kiri untuk mencari sama ada ia masih sama Terdapat kedudukan lebih ke kiri yang memenuhi syarat.

Pada masa yang sama, apabila menghadapi keadaan arr[m] > t, anda juga perlu merekodkan kedudukan m pada masa ini, kerana ini mungkin juga kedudukan yang memenuhi syarat tersebut.

Kod:

class Solution {
    public static int searchInsert(int[] arr, int t) {
        int ans = arr.length;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l)>>1);
            if (arr[m] >= t) {
                ans = m;
                r = m - 1;
            } else  {
                l = m + 1;
            } 
        }
        return ans;
    }
}

Kerumitan masa bagi keseluruhan algoritma ialah O(logN).

Cari kedudukan pertama dan terakhir elemen dalam tatasusunan yang diisih

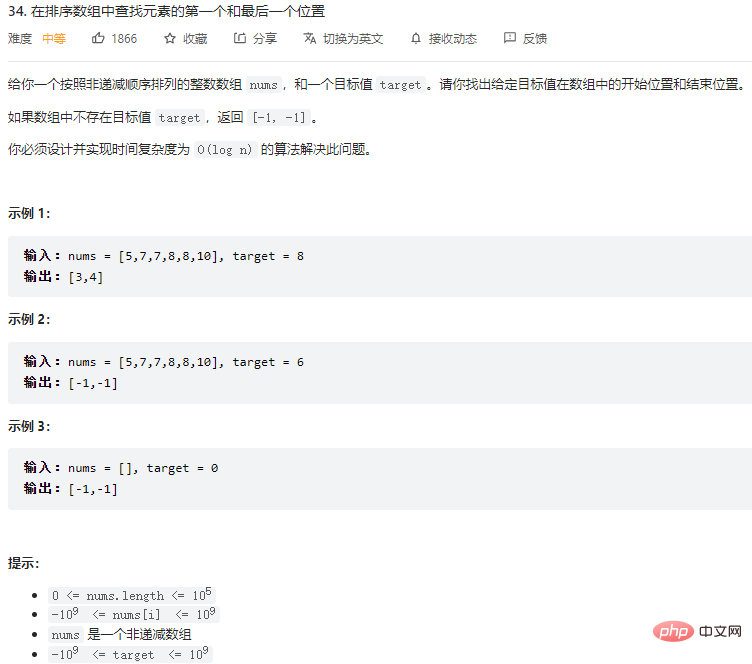
Idea

Masalah ini juga diselesaikan dengan pembahagian binari. Apabila Apabila elemen ditemui melalui pembahagian binari, jangan tergesa-gesa kembali, tetapi teruskan mencari ke kiri (kanan) untuk melihat sama ada anda boleh mencari nilai yang sepadan lebih jauh ke kiri (kanan).

Kodnya adalah seperti berikut:

class Solution {
    public static int[] searchRange(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return new int[]{-1, -1};
        }
        return new int[]{left(arr,t),right(arr,t)};   
    }
    public static int left(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               r = m - 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
    public static int right(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               l = m + 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
}

Kerumitan masa O(logN).

Masalah maksimum tempatan

Idea

Dengan mengandaikan bahawa panjang tatasusunan ialah N, mula-mula tentukan jumlah nombor pada kedudukan 0 N-1Bilangan kedudukan bukan kedudukan puncak. Kedudukan

0 hanya perlu dibandingkan dengan kedudukan 1 Jika kedudukan 0 lebih besar, kedudukan 0 ialah kedudukan puncak dan boleh dikembalikan terus. Kedudukan

N-1 hanya perlu dibandingkan dengan kedudukan N-2 Jika kedudukan N-1 lebih besar, kedudukan N-1 ialah kedudukan puncak dan boleh dikembalikan terus.

Jika kedudukan 0 dan N-1 ialah kedua-dua nilai minimum dalam pusingan terakhir perbandingan, maka tatasusunan mesti kelihatan seperti berikut:

Seperti yang dapat dilihat daripada rajah di atas, selang [0..1] ialah arah aliran pertumbuhan, dan selang [N-2...N-1] ialah arah aliran menurun.

Kemudian kedudukan puncak mesti muncul di antara [1...N-2].

Pada masa ini, anda boleh mencari kedudukan puncak dengan membahagikan Mula-mula datang ke kedudukan titik tengah, dengan mengandaikan ia adalah mid Jika nilai kedudukan titik tengah lebih besar daripada nilai di sebelah kiri dan kanan:

arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]

maka kedudukan mid ialah kedudukan puncak dan dikembalikan terus.

Jika tidak, terdapat dua situasi:

Kes 1: Nilai kedudukan pertengahan adalah lebih kecil daripada nilai kedudukan pertengahan - 1

趋势如下图：

则在[1...(mid-1)]区间内继续二分。

情况二：mid 位置的值比 mid + 1 位置的值小

趋势是：

则在[(mid+1)...(N-2)]区间内继续上述二分。

完整代码

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

时间复杂度O(logN)。

推荐学习：《java视频教程》

Atas ialah kandungan terperinci Fahami secara ringkas idea asas dan pelaksanaan dikotomi di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!